A força de elevação da asa. Parte 2
Monin Ilya Alekseevich, Ph.D., imoninpgd@gmail.comPara entender a ordem de desenvolvimento da “aviação” como um ramo da indústria e a “aerodinâmica” como uma ciência, é necessário lembrar que primeiro as primeiras aeronaves construídas por engenheiros entusiasmados da inspiração apareceram (veja a fig. 11), e só então começaram a aparecer os teóricos que criaram disciplina "Aerodinâmica" com base nos resultados da criação de engenheiros de projeto.
Na foto, o avião criado pelo motorista Henri Farman é uma alteração do avião de pequeno porte adquirido da Voisin. Ao mesmo tempo, a aeronave inicial dos irmãos Voisin começou a ser produzida apenas em 1907. No momento da compra de Farman, os aviões da Voisin só podiam saltar um pouco e voar algumas dezenas de metros. Farman, depois de uma série de alterações na aeronave original, conseguiu a oportunidade de voar mais de 1000m, enquanto ainda se virava e fazia um círculo para pousar. O vôo recorde de Farman ocorreu em 13 de janeiro de 1908. E já em 1909, a empresa dos irmãos Farman abriu sua própria produção de aeronaves de seu próprio projeto e uma escola de vôo para ensinar-lhes a arte de voar nelas (ver figura 12). A velocidade de vôo de Farman era então de cerca de 60 km / h, o que foi mostrado em um vôo recorde a uma distância de 180 km, superado em 3 horas de vôo.
Fig. 11. Uma maquete do avião de Voisin convertida para um vôo recorde por Farman em 1907-1908.
Fig. 12. O layout da aeronave "Farman IV-1910". no museu e uma foto de uma amostra genuína no aeroporto.É claro que as primeiras aeronaves iniciais eram de baixa potência, luz e baixa velocidade.
Esses parâmetros correspondem aos primeiros perfis finos convexos-côncavos, mais semelhantes à folha de compensado curvado mais simples, e não a um perfil complexo com um erro de cálculo teórico profundo.
Para referência, dou uma ilustração da transformação dos perfis das asas desde o início do século XX na indústria da aviação totalmente desenvolvida em meados dos anos 40. (ver fig. 13)
Fig. 13. Tendências no perfil da asa da aeronave da primeira metade do século XX.Após a primeira aeronave experimental leve, houve um rápido aumento no tamanho e na massa da aeronave para o transporte de uma carga útil cada vez maior. As asas finas não podiam suportar tal escala e peso de maneira que exigisse a instalação de vigas altas e fortes no interior da asa, e a própria asa deveria ser plana-convexa ou mesmo duplamente convexa para ocultar a viga de suporte atrás da bainha aerodinâmica.
Já nos anos 20, todos os perfis de asas assumiram uma aparência completamente moderna.
Na década de 1940, a indústria da aviação havia se desenvolvido tanto que começou a produzir toda uma armada de aeronave capaz de explodir cidades inteiras no pó. Mas, com um desenvolvimento tão explosivo das capacidades de produção, a base teórica permaneceu extremamente fraca.
Nos anos 30, a intensidade do desenvolvimento da aviação não permitiu a construção de novas aeronaves em um "palpite", mas exigiu a construção de uma poderosa base experimental para soprar partes de aeronaves, modelos em grande escala e aeronaves inteiramente no solo em enormes túneis de vento (ADT).
Assim, no TsAGI, em 1939, foi lançado o T-101, o maior túnel de vento da época (o segundo no mundo agora), o que tornou possível examinar toda a aeronave no solo em velocidades de vôo relevantes naquele momento.
Velocidade de fluxo 5–52 m / s
Re número por 1 ma 3,6 3.6 106
Pressão atmosférica total
Cabeça de pressão até 1,7 kPa
Temperatura ambiente de frenagem
Alcance do ângulo de ataque (α) ± 20 °
Faixa de ângulos de escorregamento (β) ± 180 °
Dimensões da peça de trabalho:
Seção do bico (elipse) 24x14 m
O comprimento da peça de trabalho é de 24 m
Dimensões dos objetos de teste:
Extensão de asa: até 18 m
Comprimento da fuselagem: até 30 m
Área da asa: até 35 m2
Desde então, os aviões se tornaram muito maiores e as velocidades de vôo foram muito mais rápidas, de modo que nenhuma aeronave moderna pode se encaixar no T-101 ADT como um todo, e no ADT mais moderno e mais rápido, apenas layouts reduzidos em grande escala ou elementos estruturais são soprados separadamente.
É verdade que pouco mudou na teoria desde o início do século passado, de modo que já no final do século XX os projetistas de aeronaves começaram a reinventar o que os projetistas do início e meados do século XX já haviam passado, mas os teóricos não explicaram. Por exemplo, darei uma visão de perfil da asa de uma aeronave acrobática, considerada a melhor da década de 1980 (veja a figura 14).
Fig. 14. Um dos perfis de asas do catálogo de perfis de aviação.A mesma linha de pensamento recorrente também é observada entre os grandes modelos de equipamento voador; isso foi expresso na criação de monstros ekranoplanes nas décadas de 1960 e 80 (Fig. 15), que não são distinguíveis das aeronaves gigantes do final da década de 1930 (Fig. 16).
Ao mesmo tempo, o próprio efeito de tela foi descoberto no início dos anos 30, no momento do pouso de grandes aeronaves multimotores com um grande acorde da asa.
Além disso, o efeito de tela foi claramente manifestado durante o pouso da aeronave recorde ANT-25 de longo alcance, quando durante um vôo de teste em 1933 o avião simplesmente não conseguiu pousar e, quando as rodas tocaram levemente o chão, a aeronave bateu e decolou novamente. Para remover esse efeito e garantir uma aterrissagem silenciosa, era necessário instalar palas de freio retráteis especiais, o que piorava bastante as qualidades de vôo da asa durante a aterrissagem.
O acorde de asa na parte mais larga da raiz do ANT-25 excedeu a altura do trem de pouso, criando condições ideais para a formação de um efeito de tela sob uma asa larga e baixa. Ao mesmo tempo, durante o pouso com tanques vazios com um peso de avião de 4000 kg e uma área de asa de 88 m², a carga média da asa em voo foi criada com menos de 50 kg / m², o que corresponde a uma pressão de velocidade de 500 Pa criada a uma velocidade de 104 km / h (29 m / s) para voar na tela. Vale ressaltar que a aeronave da época voava extremamente devagar (segundo os padrões modernos); portanto, o recorde ANT-25 tinha uma velocidade de cruzeiro de cerca de 165 km / h (máx. 246 km / h de altitude), com um alcance de vôo de 10 a 12 mil km e uma duração de 75- 80 horas seguidas.
A.
B.
B.
Fig. 15. WIG "Monstro Cáspio": a.) Em voo. B.) Ainda na água, rosto cheio. c.) Estacionário em projeção frontal.A.
B.
Fig.16. Avião gigante ANT-20 "Maxim Gorky", 1939 a) Seção esquemática. B) Fotos no aeroporto e durante o pouso.Zonas estagnadas durante o fluxo de ar em torno de corpos de formas complexas como ferramenta para formar um perfil virtual das asas.
Muitas vezes existem casos. Quando é necessário construir linhas de fluxo de ar em torno de corpos cuja forma dificilmente pode ser chamada de aerodinâmica.
É claro que o ar não fluirá obedientemente em torno de todos os cantos e sulcos do corpo, mas seguirá com reviravoltas suaves, riscando as fossas e enchendo-as de vórtices de fluxos rasgados de zonas estagnadas.
Se considerarmos a presença de zonas estagnadas como volumes sólidos adicionais do próprio perfil, a geometria do fluxo em torno dos elementos aerodinâmicos conhecidos por nós assumirá uma forma completamente diferente.
É interessante que esse método de encontrar um protótipo de asa condicional equivalente também seja usado na aerodinâmica aplicada existente. De qualquer forma, o método de construção de um "corpo semi-infinito fictício" em torno de uma asa sólida é descrito no livro [3] em três páginas (p. 435-437), enquanto a borda de uma camada limite inibida grossa é escolhida como os limites da asa fictícia, ou seja, aumentando a asa nossas zonas muito estagnadas em "bolhas de separação" ou zonas turbulentas com uma interrupção completa do fluxo acima da asa. Nesse caso, a pressão na asa sólida proveniente do fluxo de ar de alta velocidade é considerada igual à pressão desse fluxo no "corpo fictício". Acontece que a pressão é transferida do jato de alta velocidade para a asa sólida através de uma camada suficientemente espessa de ar inativo da camada inibida nos limites (zona estagnada) sem nenhuma distorção.
Vamos considerar em detalhes o processo de fluxo suave em torno de jatos de alta velocidade de diferentes perfis de perfis de asas e distinguir várias "zonas estagnadas".
O caso de aderência completa do fluxo à asa em pequenos ângulos de ataque não acrescenta muita novidade (veja a fig. 17), mas uma pequena zona estagnada aparece na carenagem frontal, semelhante a um pequeno bico afiado na cabeça redonda do pássaro.
O elemento parece pequeno, mas é extremamente importante para entender o fenômeno do "fluxo" em geral.
Considere o perfil usual da asa em vôo horizontal com jatos destacados distintos, primeiro com um ângulo de ataque zero (veja a fig. 18) e, em seguida, a mesma asa com um grande ângulo de ataque (veja a fig. 20).
Fig. 17. Um perfil de asa com um fluxo ao redor sem quebras nos planos da asa, mas com uma pequena zona de desaceleração completa do fluxo no nariz da asa.
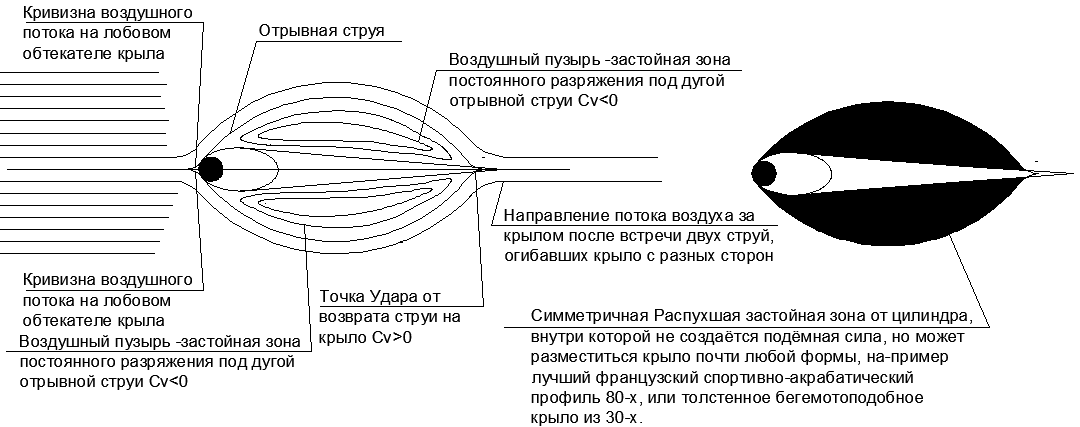Fig. 18. O perfil da asa com fluxo quebra nos planos da asa em ângulo de ataque zero e seu “corpo fictício”.Observando o forte aumento do “corpo fictício” em comparação com a carenagem frontal inicial, torna-se claro o quão surpreendentemente baixa resistência frontal é obtida para corpos longos em forma de eixo, por exemplo, para fuselagens de aeronaves.
A racionalização de tais formas atinge Cx = 0,06, enquanto para uma bola da mesma seção Cx = 0,4..0,5 e para uma placa plana Cx = 1.
Acontece que a descarga sob os jatos destacados na projeção frontal não é criada. Tudo o que resta é pousar o jato de separação em uma superfície reta paralela ao vetor de velocidade, para que um componente longitudinal à velocidade não apareça após o impacto. Uma fuselagem cilíndrica longa com uma carenagem frontal ovóide alongada lida perfeitamente com essa tarefa. Acontece que o arrasto da enorme fuselagem é igual à resistência da bola na ponta do nariz afilado (veja a figura 19.)
A relação entre o diâmetro da bola na carenagem do nariz e o diâmetro da fuselagem depende da velocidade do vôo, e quanto maior a velocidade do vôo, mais estreito o arredondamento do nariz se torna, empurrando o fluxo de ar. A energia crescente do fluxo que se aproxima com um valor constante da seção frontal requer espalhar uma quantidade cada vez menor de ar para os lados da fuselagem, mantendo uma seção constante do "corpo fictício" atrás da carenagem. No supersônico, o raio de curvatura do cone do nariz degenera até certo ponto, mas essa é uma história completamente diferente.
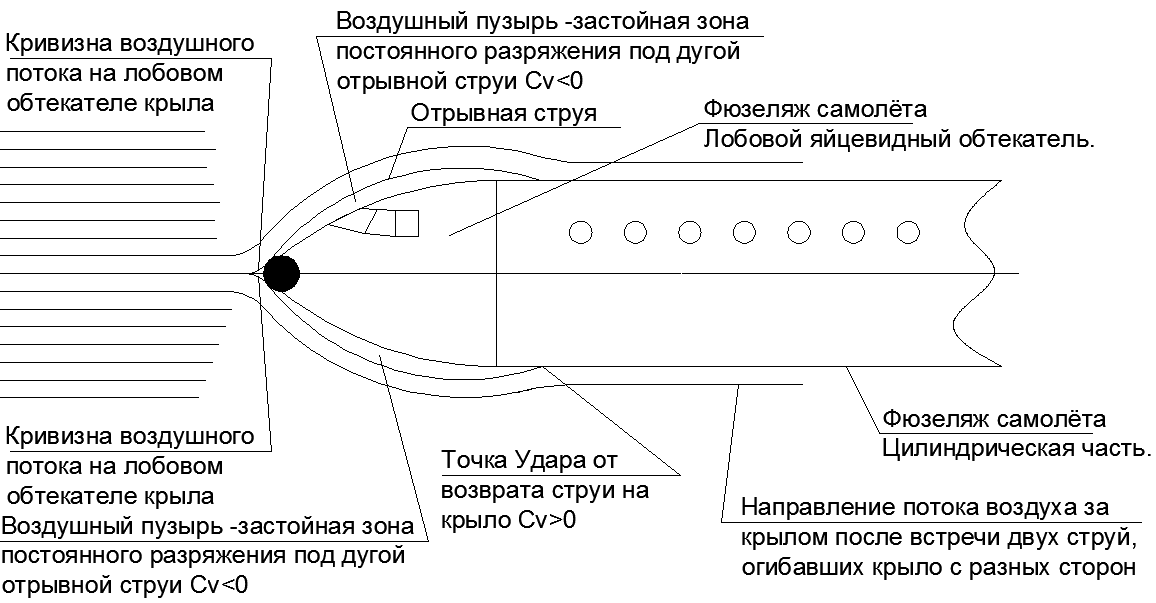
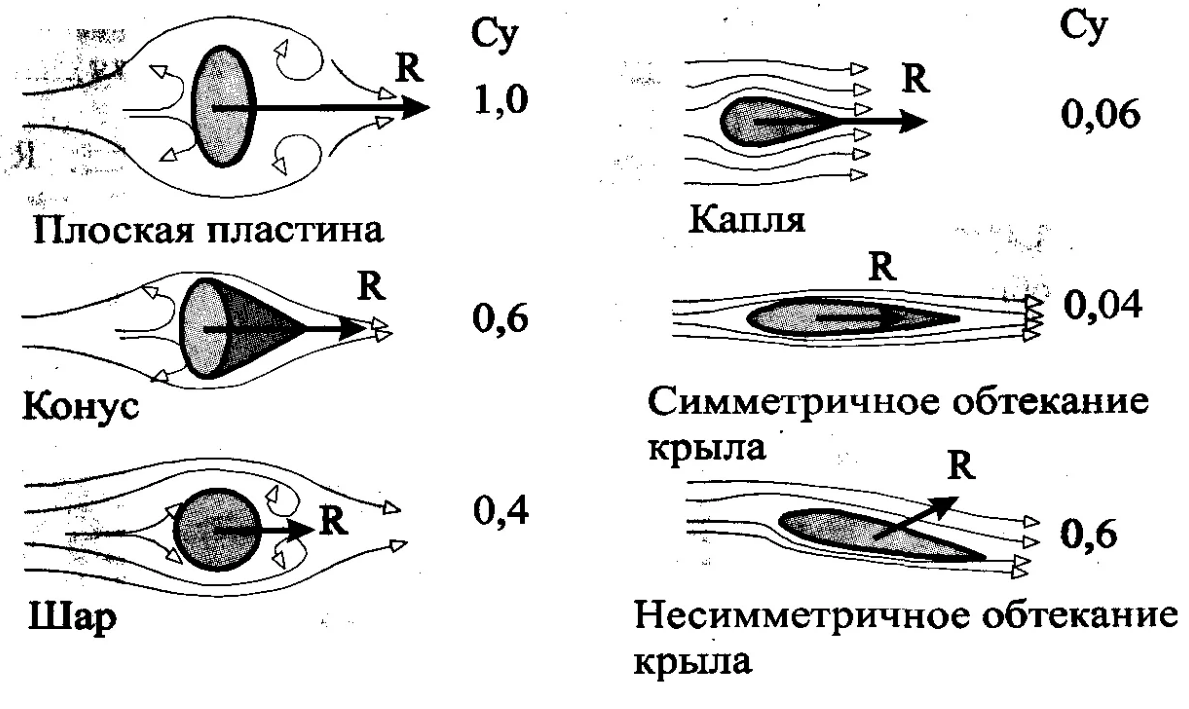
Fig. 19. O modo de fluxo ao redor da fuselagem com jatos destacáveis, sob os quais é criada uma zona de resistência zero ao vôo. Toda a resistência da fuselagem é igual à resistência aerodinâmica da bola na carenagem do nariz. E ilustrações acompanhantes de livros didáticos sobre o tema da resistência quando o ar flui por vários corpos.Agora consideramos o comportamento de zonas turbulentas separadas com uma asa com um grande ângulo de ataque (veja a Fig. 20).
Primeiro, é necessário traçar a trajetória do fluxo de separação acima da zona estagnada até encontrar o fluxo sob a asa da aeronave. Considerando que o perfil da carenagem frontal da asa é cilíndrico simétrico, os jatos destacáveis têm potência e trajetória iguais, ou seja, também são simétricos.
Para a asa horizontal, já recebemos uma bolha destacável simétrica de dois lados com o fechamento dos jatos da asa nos mesmos lugares.
Ao dar à asa um grande ângulo de ataque, o padrão dos jatos de separação muda. Ao mesmo tempo, os tamanhos de "Bolhas separadas" = "Zonas estagnadas" acima e abaixo da asa começam a diferir dramaticamente em volume.
Como resultado, uma asa muito inchada com um achatamento significativo do plano inferior em comparação com a enorme cúpula da bolha de separação no plano superior da asa se tornará um "corpo fictício". Curiosamente, o perfil virtual equivalente de um “corpo fictício” em um grande ângulo de ataque da asa com bolhas separadas infladas no plano superior da asa é surpreendentemente semelhante ao conhecido avião ECIP. (ver fig. 21)
Fig. 20. O perfil da asa com fluxo quebra nos planos da asa com um grande ângulo de ataque e seu “corpo fictício”.
Fig.21. WIG EKIP. Um modelo de um modelo WIG em perspectiva e o atual modelo WIG menor (que não decolou devido à parada do projeto).Ou seja, no ECIP de Ekranolet, foi uma boa idéia controlar a zona estagnada na parte "sombra" traseira do casco, o que permitiu que o jato de arranque fosse depositado na asa na parte superior da cúpula, o que proporciona maior sustentação e reduz a resistência aerodinâmica ao vôo.
Acontece que o autor do EKIP não foi tão inventivo, oferecendo um design semelhante ao de um hipopótamo como uma aeronave.
É verdade que o ECIP não deve voar muito rápido e com grandes ângulos de ataque do perfil fino inicial (cerca de 15 graus), com um arrasto alto correspondente.
A enorme quantidade de espaço de carga em uma asa voadora é mais do que compensada por alguma deterioração da aerodinâmica. Ao mesmo tempo, a asa de aeronave estruturalmente inutilizável parece muito mais atraente do que uma aeronave tradicional, com a separação das funções de uma fina “asa de apoio” e “fuselagem de carga e passageiro”. Mas apenas para um vôo estável, você ainda precisa adicionar uma viga longa para acomodar a cauda, como na asa voadora gigante do ANT-20 "Maxim Gorky".
Uma expansão significativa da asa (um aumento no acorde) faz do avião EKIP também uma WIG pronunciada em termos de suas propriedades aerodinâmicas ao voar perto do solo. Portanto, ao voar na tela, o "corpo fictício" da asa com um grande ângulo de ataque se transforma em um ferro estranho, onde o pequeno bico do nariz da zona de frenagem da asa infla para o tamanho de uma enorme cunha estagnada sob a asa (veja a figura 22).
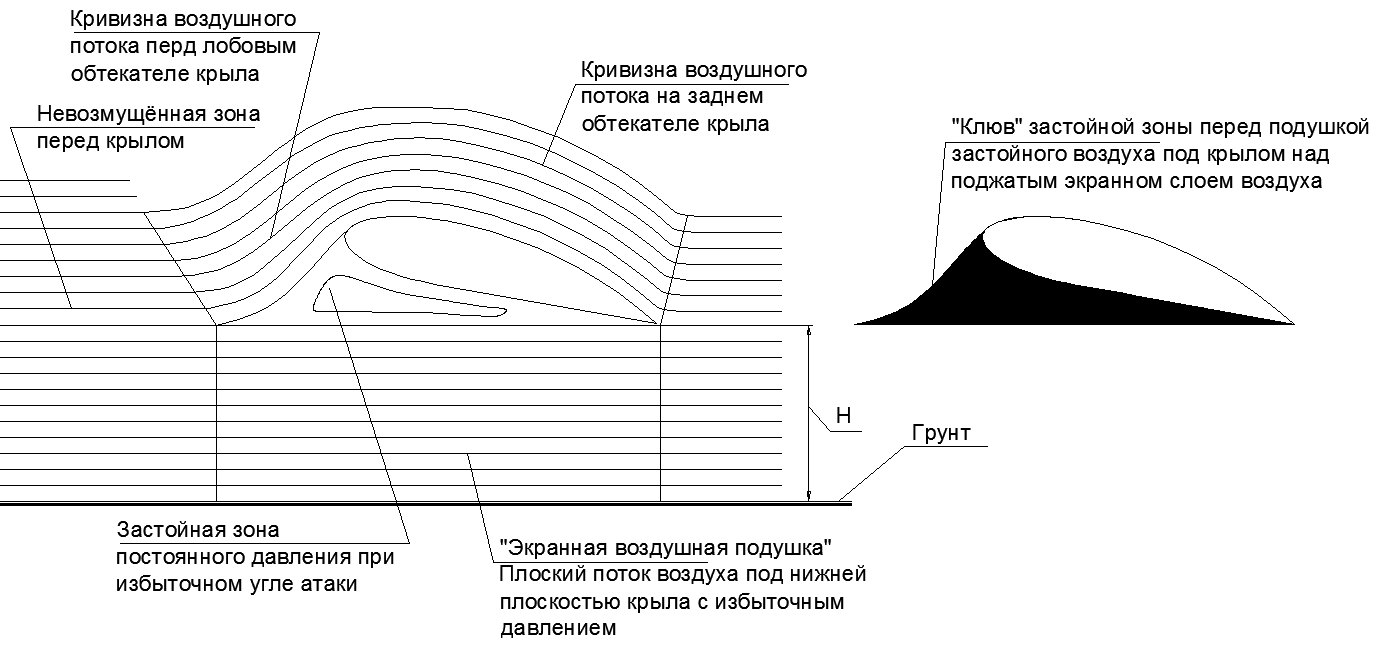Fig. 22. O perfil da asa ao voar sobre a tela com um grande ângulo de ataque e seu "corpo fictício".Dentro deste ferro pontiagudo, é possível colocá-lo como perfis de EKIP e VVA-14 Ekranoletos (Bartini), ou uma asa ultra-grossa como a do ANT-20 "Maxim Gorky".
Aeronaves com uma asa muito grossa eram populares na década de 1930 na URSS, quando a maior aeronave pré-guerra ANT-20 "Maxim Gorky" foi criada. A asa desta aeronave era tão grossa e larga que várias cabines foram colocadas nos compartimentos das raízes da asa, onde uma pessoa caminhava até sua altura máxima (veja a Fig. 16.).
É verdade que este monstro voou com uma velocidade de cruzeiro de apenas 198 km / h (máximo de 220 km / h).
Se o ANT-20 encurtar levemente as seções finais da asa, deixando apenas a parte mais grossa central, a aeronave se tornará semelhante ao posterior "Monstro Cáspio" Rostislav Alekseev.
É interessante comparar o "Maxim Gorky" de tamanho aproximado da década de 1930 com o "Monstro Cáspio" da década de 60 (consulte a tabela 5)
Tab. 5. Características comparativas da aeronave ANT-20 "Maxim Gorky" 1934 e WIG KM "Caspian Monster" 1966.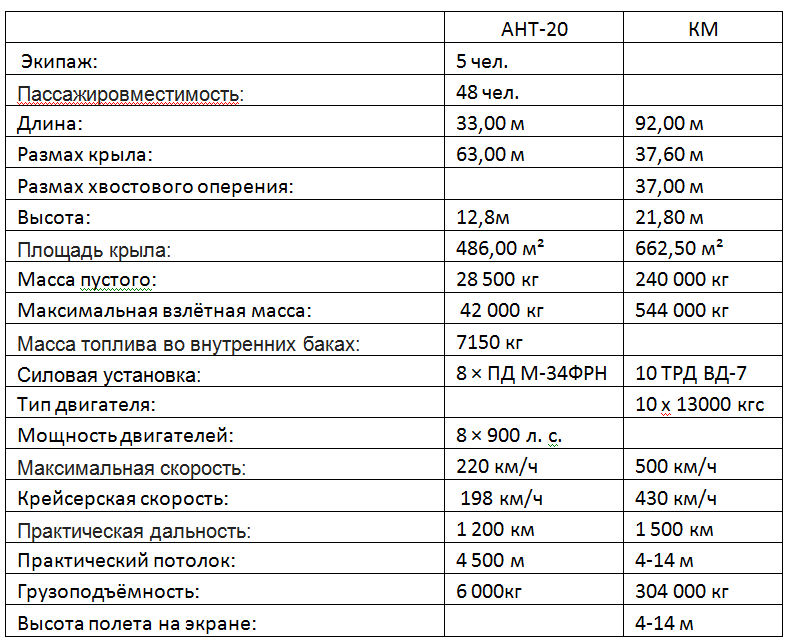
A tabela contém dados de referência que devem ser interpretados de alguma forma.
Vamos primeiro por uma maneira simples de comparar diretamente números homogêneos, dividindo-se.
Peso máximo: 544/42 = 13 vezes
Área da asa: 662/486 = 1,36 vezes
Carga específica da asa: 13 / 1,36 = 9,5 vezes
Velocidade de cruzeiro: 430/198 = 2,17 vezes
A diferença de velocidade na velocidade de cruzeiro: 2,17 ^ 2 = 4,71 vezes
Potência das usinas: (10 * 1300 * 9,81 * 430 / 3,6) / (8 * 900 000 * 0,735) = 28,8 vezes
Carga útil considerando o combustível: 304 / (42-28,5) = 22,51.
Alcance prático: 1500/1200 = 1,25
De acordo com a relação de economia de combustível ANT-20 = 7150 / (1200 * 6) = 0,993 l / (t * km)
A voracidade do KM não é conhecida, mas pode ser estimada através de potência e velocidade.
Ao calcular o consumo específico por voracidade de referência 0,8 kg / (kgf * h) para o motor VD-7.
Consumo de pós-combustor durante a aceleração da água 10 * 13000 * 0,8 = 104 000 kg / h
Se você levar em consideração a duração de um voo de cruzeiro na tela com apenas dois dos dez motores disponíveis para aceleração e acesso à Tela, a economia aumentará.
Para cruzeiro com dois motores 2 * 13 000 * 0,8 = 20 800 kg / h
Tempo de voo 1500/430 = 3,5 horas
Durante um vôo a um alcance máximo de 1500 km, o KM devorará pelo menos 104 * 0,5 + 3,5 * 20,8 = 100 toneladas de combustível.
E a carga útil será de cerca de 200 toneladas.
A economia de combustível de KM resultará em 100.000 / (1500 * 200) = 0,333 l / (t.km).
Conclusões das relações obtidas:
1. Em termos de economia de combustível, o KM pode ser otimista três vezes mais econômico que o ANT-20.
Agora, o moderno avião de passageiros Airbus A380 possui uma modificação de carga A380F com a capacidade de transportar cargas de até 150 toneladas a uma distância de 10.370 km. A massa máxima de decolagem é de 560 toneladas (a massa da própria aeronave é de 280 toneladas). Calculamos a economia para a versão de carga a partir desses indicadores e fornecemos 130 toneladas de combustível e 150 toneladas de carga a uma distância de 10370 km: 130.000 / (150 * 10370) = 0,0835 l / (t * km).
Em termos de passageiros, o indicador é diferente: “Entre os transatlânticos, o mais econômico é de três litros de combustível por passageiro a cada cem quilômetros (54 milhas náuticas) da rota. Segundo a Airbus [5], por passageiro, o A380 consome 17% menos combustível do que a “maior aeronave moderna” (aparentemente, o Boeing 747 se destina). „
Ou seja, com uma contagem de teste de 850 passageiros com bagagem e assentos, temos um indicador próximo ao cálculo para a versão de carga.
Acontece que não apenas começamos a voar 4-5 vezes mais rápido nos últimos 80 anos, mas também melhoramos a eficiência de combustível mais de 10 vezes do ANT-20 e 4 vezes do Ekranoplan KM. Embora apenas 20 anos atrás, nosso airbus voou 5 vezes mais rápido que o ANT-25. A recente desaceleração nas aeronaves de passageiros é causada pela luta por voos com baixo consumo de combustível.
2. A velocidade de cruzeiro do KM é tão alta à força, pois a uma velocidade mais baixa ele simplesmente não consegue voar na tela. A condição de vôo na tela é o cumprimento da desigualdade "Speed head"> "Average wing load", ou seja,
Pv = 8560Pa a 430 km / h (120m / s)> 544000 * 9,81 / 662,5 = 8055Pa.
3. A segurança de vôo de uma aeronave gigante de baixa velocidade dos anos 30 é muito melhor do que a de uma aeronave alada de alta velocidade dos anos 60, correndo quase incontrolavelmente entre navios de movimento lento e as onipresentes aves aquáticas.4. O custo da operação de ekranoplanes baseados no mar é muito mais caro do que para aeronaves terrestres de alta altitude. Isso ocorre devido ao número excessivo de motores necessários apenas para iniciar a partir da água e sair para o voo de tela, bem como devido à extrema agressividade da água do mar quando exposto a motores e projetos ekranoplan ao voar nas nuvens devido a salpicos de ondas próximas do mar.5. Para o Ekranoplan KM, a qualidade da asa ao voar em dois motores é igual à razão entre seu empuxo e o peso do Ekranoplan K = 544 / (13 * 2) = 20,9. Assim, a eficiência aerodinâmica de um Ekranoplan grande e pesado está no nível de eficiência dos melhores grandes aviões modernos com qualidade de planador da ordem de K = 18-20.6. O mistério para mim é a tríplice diferença de eficiência do Ekranoplan KM com o Airbus 380F: Por que, com a mesma qualidade da estrutura da aeronave, a Airbus tem 4 vezes melhor economia de combustível?Ou todo esse segredo está oculto na terrível gula dos antigos motores turbo-soviéticos em comparação com os modernos motores turbofan com alto grau de desvio?:
1. « », .., , , 1986.-413.
2. «» 1, .., , , 2018,-496.
3. «», . .., , ...,2017,-607.