Familiaridade com a rede neural mais simples e sua implementação passo a passo

Uma vez me deparei com um livro chamado "Crie sua rede neural" , de autoria de Tarik Rashid . Ao contrário de muitos outros livros sobre redes neurais, tudo foi apresentado em uma linguagem simples, com um número suficiente de exemplos e dicas

Inspirado por este livro, quero passar por ele passo a passo - a saber, sua parte prática - escrevendo o código para uma rede neural simples .
Este artigo é para aqueles que desejam fazer redes neurais e aprendizado de máquina, mas até agora têm dificuldade em entender esta incrível área da ciência. O esqueleto mais simples do código de uma rede neural será descrito abaixo, para que muitos entendam o princípio mais simples de construção e interação de tudo o que essa rede neural consiste.




Teorias sobre aprendizado de máquina e redes neurais no Habré são suficientes. Mas se alguém precisar, deixarei alguns links no final do artigo. E agora, começaremos a escrever código diretamente e escreveremos em Python , recomendo usar o Jupyter-Notebook ao escrever código

Etapa 1. Inicialização da rede

Primeiro, é claro, precisamos inicializar todos os componentes ativos da nossa rede

# numpy —    Python,        import numpy #  scipy.special , -scipy    , ,  ,      ,       ,   - " " import scipy.special #,      import matplotlib.pyplot #     class neuralNetwork: #     def __init__(self, inputnodes, hiddennodes, outputnodes, learningrate): #     ,   ,   ,  ) #     ,  ,   self.inodes = inputnodes self.hnodes = hiddennodes self.onodes = outputnodes #    , wih -       ,    who-       self.wih = numpy.random.rand(self.hnodes, self.inodes) self.who = numpy.random.rand(self.onodes, self.hnodes) #   -  ,  ,  ,    ,     ,     ,  ,  ,   self.lr = learningrate #  -   self.activation_function = lambda x: scipy.special.expit(x) 

Sigmoid

Essa função pertence à classe de funções contínuas, pega um número real arbitrário (ou seja, não necessariamente um número inteiro) na entrada e fornece um número real no intervalo de 0 a 1 na saída .

Em particular, grandes números negativos (módulo) se transformam em zero e grandes números positivos se transformam em um .

Sua saída é bem interpretada como o nível de ativação dos neurônios: da ausência de ativação (0) à ativação totalmente saturada (1).

O sigmóide é expresso pela fórmula:



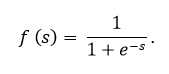
O gráfico da função sigmóide de acordo com a figura abaixo:



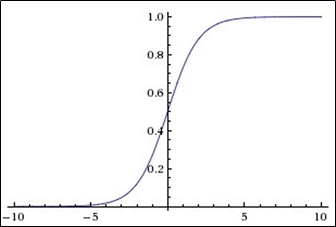
A função sigmóide é:

• contínuo
• monotonamente aumentando;
• diferenciável.

Nesse código, o sigmoide está presente, como você pode ver, sob o nome expit (x)

Um pouco sobre a aparência de um nó em uma rede neural

A figura mostra o máximo desse nó, mas geralmente é apresentado na forma de um círculo, não de um retângulo. Como vemos, dentro de um retângulo (bem, ou um círculo) - tudo isso é abstrato, existem 2 funções:

A 1ª Função está envolvida no fato de receber toda a entrada, levando em consideração os pesos, dados e, às vezes, até o neurônio de deslocamento (um neurônio especial que simplesmente permite que os gráficos se movam e não se misturem em uma pilha feia, isso é tudo)

A 2ª função assume como parâmetro o mesmo valor que a primeira função soma, e essa segunda função é chamada de função de ativação. No nosso caso, um sigmóide

Continuamos :

Parte 2. Treinamento em redes neurais

 def train(self, inputs_list, targets_list): #       inputs = numpy.array(inputs_list, ndmin=2).T #     input targets = numpy.array(targets_list, ndmin=2).T #  targets #      hidden_inputs = numpy.dot(self.wih, inputs) #  ,       .    ,       hidden_inputs (1 ),        -   (2 ) hidden_outputs = self.activation_function(hidden_inputs) #    ()  final_inputs = numpy.dot(self.who, hidden_outputs) #  ,     final_outputs = self.activation_function(final_inputs) #   ( - ) output_errors = targets - final_outputs #      ,    <b>  </b>,   <b>       </b>(      ) hidden_errors = numpy.dot(self.who.T, output_errors) #        ( ,      ) self.who += self.lr * numpy.dot((output_errors * final_outputs * (1.0 - final_outputs)), numpy.transpose(hidden_outputs)) #       (       ) self.wih += self.lr * numpy.dot((hidden_errors * hidden_outputs * (1.0 - hidden_outputs)), numpy.transpose(inputs)) 

E agora estamos chegando ao fim

Parte 3. Interrogatório de uma rede neural

 #  ,      def query(self, inputs_list): #         inputs = numpy.array(inputs_list, ndmin=2).T #      hidden_inputs = numpy.dot(self.wih, inputs) #  ,     hidden_outputs = self.activation_function(hidden_inputs) #      final_inputs = numpy.dot(self.who, hidden_outputs) #     ,     final_outputs = self.activation_function(final_inputs) return final_outputs 

Trazemos isso para o fim

 #     ,  ,  (  <b></b>-    , ,   input_nodes = 3 hidden_nodes = 3 output_nodes = 3 #    -   , ... 0.3! learning_rate = 0.3 #   (n    neuralNetwork ,      __init__ ,        n = neuralNetwork(input_nodes,hidden_nodes,output_nodes, learning_rate) 

PS

Acima foi apresentado um modelo computacionalmente mais simples de uma rede neural. Mas nenhuma aplicação específica foi mostrada.

Se desejar, você pode ir além, adicionando a capacidade de reconhecer texto manuscrito no código MNIST , para isso você pode descobrir completamente (e apenas se divertir) com este arquivo jupyter , minha tarefa era demonstrar o código e, se possível, mastigar na rede e por que respostas

PPS

Abaixo você encontrará links úteis:

1. Link para o Github Tarik ->
2. seu livro ->
3. Teoria da Aprendizagem Mecânica ->
Teoria da Aprendizagem Mecânica ->
5. Teoria da aprendizagem da máquina ->