Julia e o enxame de partículas

Continuamos estudando os métodos de otimização multidimensional, e o próximo da fila é o método de enxame de partículas, que busca um mínimo global.

Teoria

• Wikipedia
• Vários métodos de enxame de partículas e suas topologias
• Um enxame de partículas em Python e C #
• Método de otimização de um pacote de selos

O algoritmo é bastante simples:

A posição de cada partícula em um determinado momento é calculada pela fórmula:

Onde $$$p_i$- coordenada da melhor solução para uma partícula específica, $$$g_i$- a coordenada da melhor solução para todas as partículas para esta época, $$$C_p$e $$$C_g$- fatores de ponderação (selecionados para um modelo específico), $$$A_c$É o coeficiente de inércia, pode ser feito dependente do número de uma era, então as velocidades das partículas mudam suavemente.

Funções de teste

Como é muito bom observar o trabalho do método, teremos mais funções de teste:

parabol(x) = sum(u->u*u, x) # f(0,0) = 0, x_i ∈ [-10,10] shvefel(x) = sum(u-> -u*sin(sqrt(abs(u))), x) # f(420.9687,420.9687) = -819?, x_i ∈ [-500,500] rastrigin(x) = 10*length(x) + sum(u->u*u-10*cos(2*pi*u), x) # f(0,0) = 0, x_i ∈ [-5,5] ekly(x) = -20exp(-0.2sqrt(0.5(x[1]*x[1]+x[2]*x[2]))) - exp(0.5(cospi(2x[1])+cospi(2x[2]))) + 20 + ℯ # f(0,0) = 0, x_i ∈ [-5,5] rosenbrok(x) = 100(x[2]-x[1]*x[1])^2 + (x[1]-1)^2 # f(0,0) = 0, x_i ∈ [-5,5] bill(x) = (1.5-x[1]+x[1]*x[2])^2 + (2.25-x[1]+x[1]*x[2]*x[2])^2 + (2.625-x[1]+x[1]*x[2]^3)^2 # f(3,0.5) = 0, x_i ∈ [-5,5] boot(x) = (x[1]+2x[2]-7)^2 + (2x[1]+x[2]-5)^2 # f(1,3) = 0, x_i ∈ [-10,10] bukin6(x) = 100sqrt(abs(x[2]-0.01x[1]*x[1])) + 0.01abs(x[1]+10) # f(-10,1) = 0, x_i ∈ [-15,-5; -3,3] levy13(x) = sinpi(3x[1])^2 + (1+sinpi(3x[2])^2)*(x[1]-1)^2 + (1+sinpi(2x[2])^2)*(x[2]-1)^2 # f(1,1) = 0, x_i ∈ [-10,10] himmelblau(x) = (x[1]^2+x[2]-11)^2 + (x[1]+x[2]^2-7)^2 # f(3,2)... = 0, x_i ∈ [-5,5] camel3humped(x) = 2x[1]^2 - 1.05x[1]^4 + x[1]^6 /6 + x[1]*x[2] + x[2]^2 # f(0,0) = 0, x_i ∈ [-5,5] izom(x) = -cos(x[1])*cos(x[2])*exp(-( (x[1]-pi)^2 + (x[2]-pi)^2 )) # f(π,π) = -1, x_i ∈ [-100,100] holdertable(x) = -abs(sin(x[1])*cos(x[2])exp(abs( 1-sqrt(x[1]^2+x[2]^2)/pi ))) # f(±8.05502,±9.66459) = -19.2085, x_i ∈ [-10,10] shaffer4(x) = 0.5 + (cos(sin(abs(x[1]^2-x[2]^2)))^2-0.5) / (1+0.001(x[1]^2+x[2]^2))^2 # f(0,1.25313) = 0.292579, x_i ∈ [-100,100] 

E, de fato, o próprio MRC:

 function mdpso(; nparts = 50, ndimes = 2, ages = 50, #   lover = [-10 -10], upper = [10 10], C1 = [1.9 1.9], #  - C2 = [1.8 1.8], Ac = [0.1 0.1], ) minind = 0 V = zeros(nparts,ndimes) #   n  n X = zeros(nparts,ndimes) funmin = -Inf Fmin = Inf Fbest = fill(Fmin, nparts) funx = zeros(nparts) xmem = zeros(nparts,ndimes) xbest = zeros(ndimes) #   #      for i in 1:nparts, j in 1:ndimes X[i,j] = randomer(lover[j], upper[j]) end for i in 1:ages for j in 1:nparts funx[j] = fun(X[j,:]) if funx[j] < Fbest[j] Fbest[j] = funx[j] xmem[j,:] = X[j,:] end end #      ploter(lover, upper, X, funx, i); funmin = minimum(funx) minind = argmin(funx) if funmin < Fmin Fmin = funmin xbest[:] = X[minind,:] end for j in 1:nparts, k in 1:ndimes R1 = rand() R2 = rand() V[j,k] = Ac[k]*V[j,k] + C1[k]*R1*(xmem[j,k] - X[j,k]) + C2[k]*R2*(xbest[k] - X[j,k]) X[j,k] += V[j,k] end println("Age № $i\n xbest:\n $(xbest[1]) $(xbest[2])") println("Fmin: $Fmin\n") end f = open("$fun.txt","w") #      write(f,"C1 = $C1, C2 = $C2, Ac = $Ac, lower = $lover, upper = $upper, ages = $ages, parts = $nparts") close(f) end 

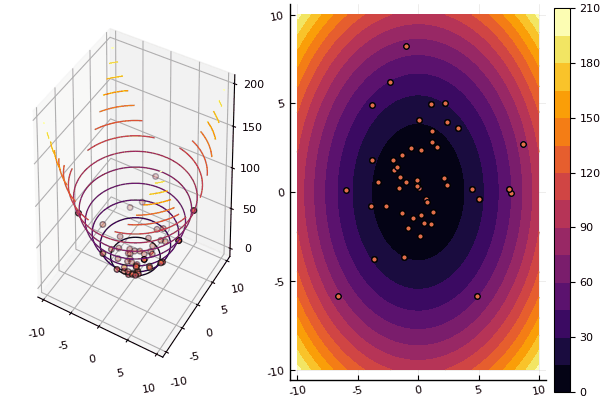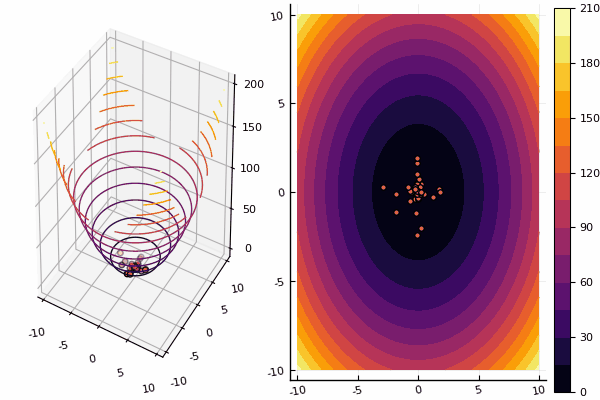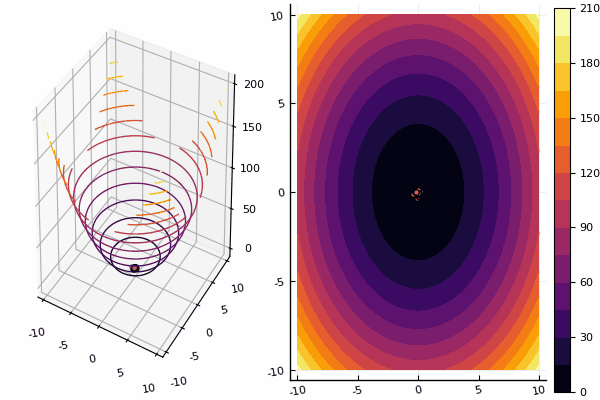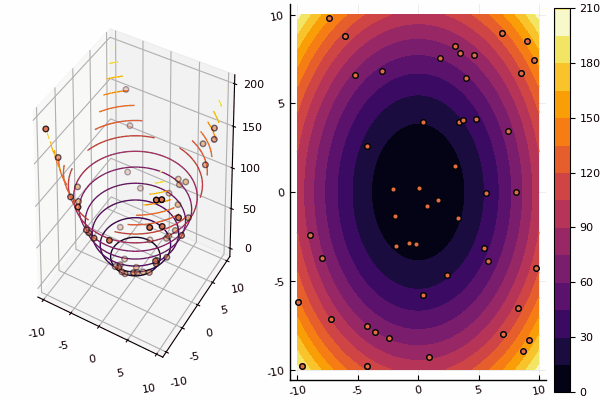
Nos desenhos, porém, o cálculo leva mais tempo, mas é mais bonito:

 using Plots pyplot() function ploter(l, u, xy, z, n_age ) contour(Xs, Ys, Zs, fill = true); #    (   ) #   ,       scatter!(xy[:,1], xy[:,2], legend = false, xaxis=( (l[1], u[1])), yaxis=( (l[2], u[2])) ); #savefig("$fun $n_age.png") #        end fun = bill low = [-4 -4] up = [4 4] Xs = range(low[1], stop = up[1], length = 80) Ys = range(low[2], stop = up[2], length = 80) Zs = [ fun([xy]) for y in Ys, x in Xs ] surface(Xs, Ys, Zs) xaxis!( (low[1], up[1]), low[1]:(up[1]-low[1])/5:up[1] ) yaxis!( (low[2], up[2]), low[2]:(up[2]-low[2])/5:up[2] ) 

 mdpso(C1 = [1.2 1.2], C2 = [1.1 1.1], Ac = [0.08 0.08], lower = [-4 -4], upper = [4 4], ages = 30) 

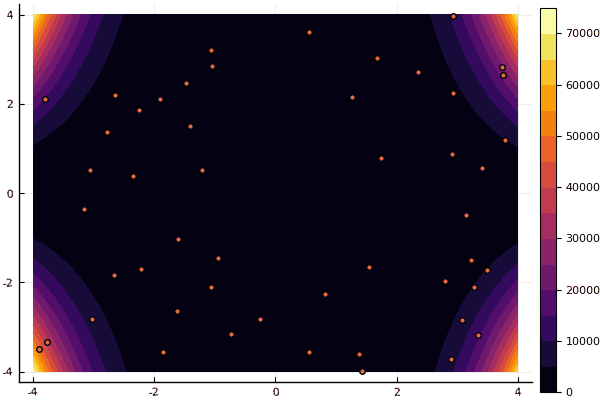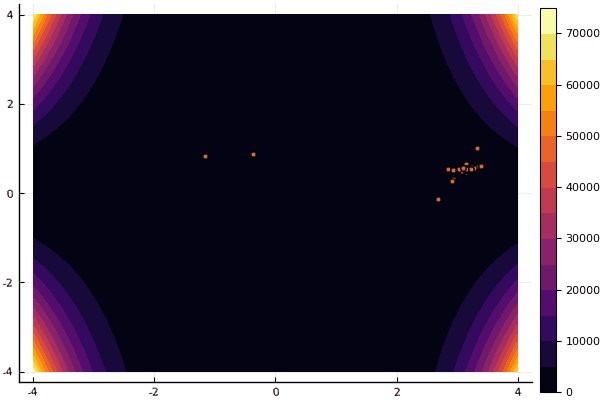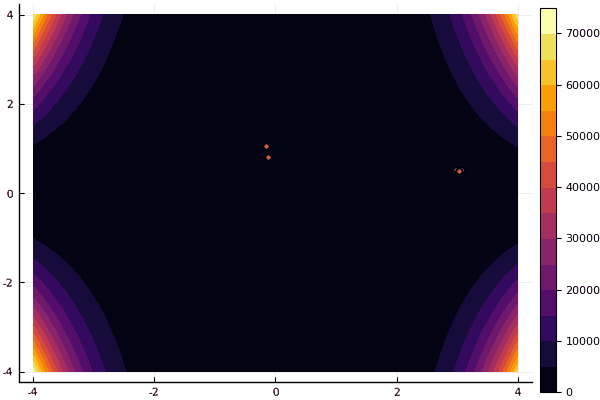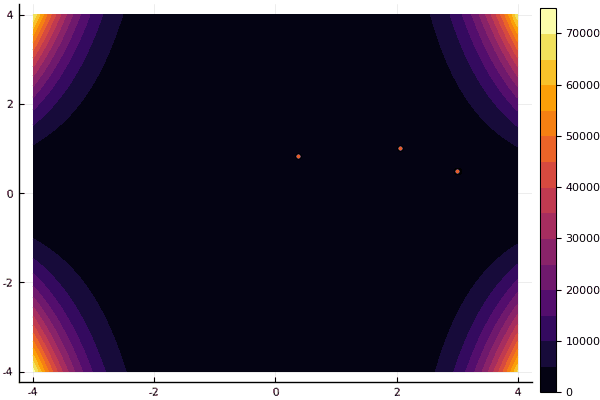
 fun = ekly mdpso(C1 = [1.7 1.7], C2 = [1.7 1.7], Ac = [0.07 0.07], lower = [-5 -5], upper = [5 5], ages = 15) 

 fun = himmelblau mdpso(C1 = [1.1 1.1], C2 = [1.0 1.0], Ac = [0.09 0.09], lower = [-5 -5], upper = [5 5], ages = 20, parts = 50) 

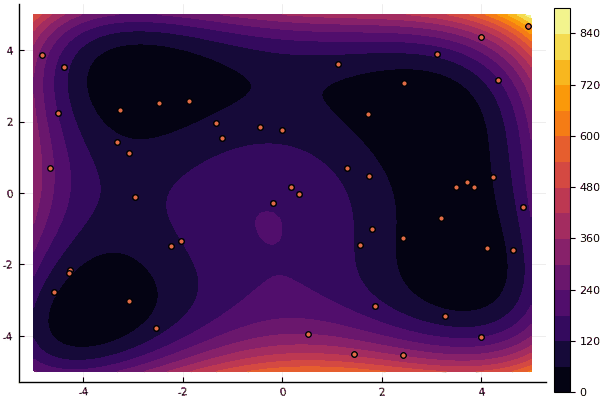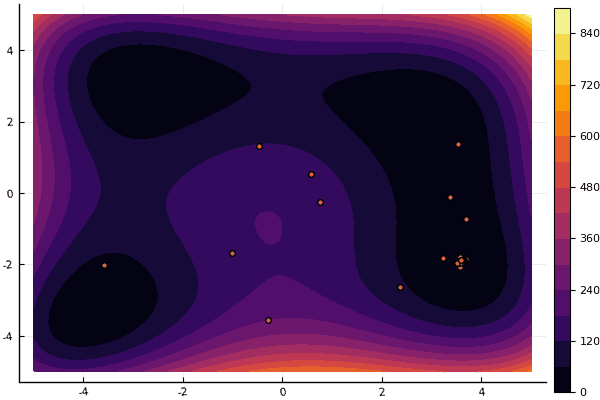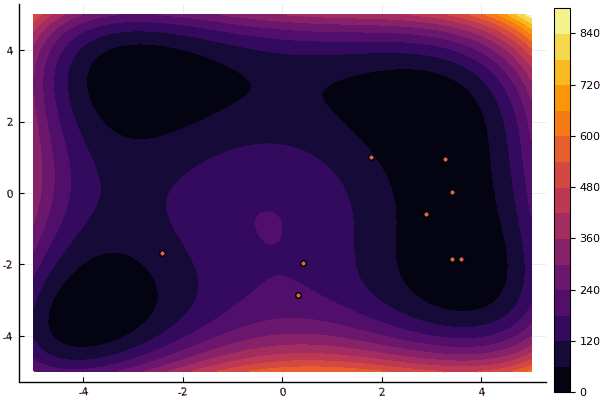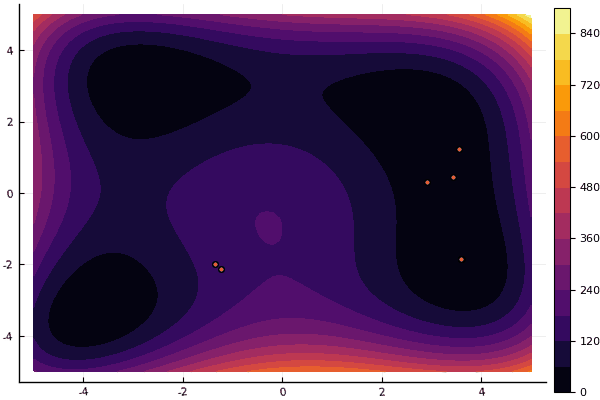
 fun = holdertable mdpso(C1 = [1.1 1.1], C2 = [1.0 1.0], Ac = [0.09 0.09], lower = [-10 -10], upper = [10 10], ages = 20, parts = 50) 

 fun = levy13 mdpso(C1 = [1.1 1.1], C2 = [1.0 1.0], Ac = [0.09 0.09], lower = [-10 -10], upper = [10 10], ages = 20, parts = 50) 

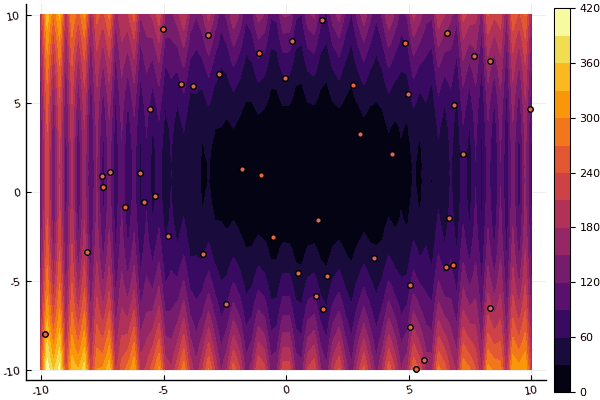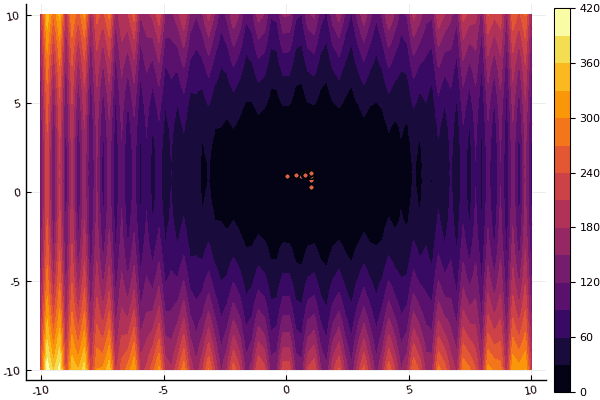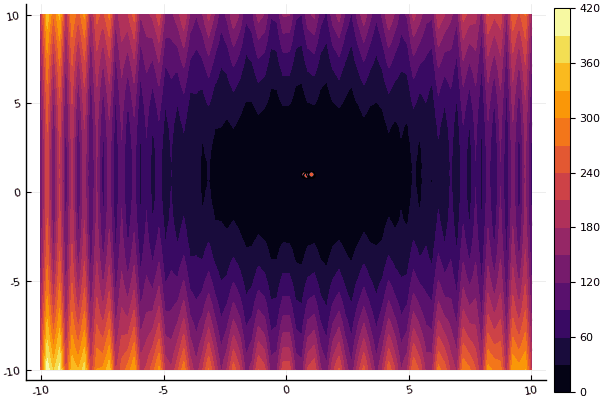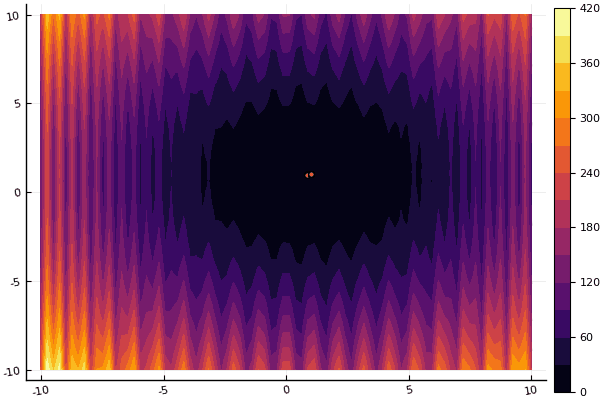
 fun = shaffer4 mdpso(C1 = [1.1 1.1], C2 = [1.0 1.0], Ac = [0.09 0.09], lower = [-100 -100], upper = [100 100], ages = 20, parts = 50) 

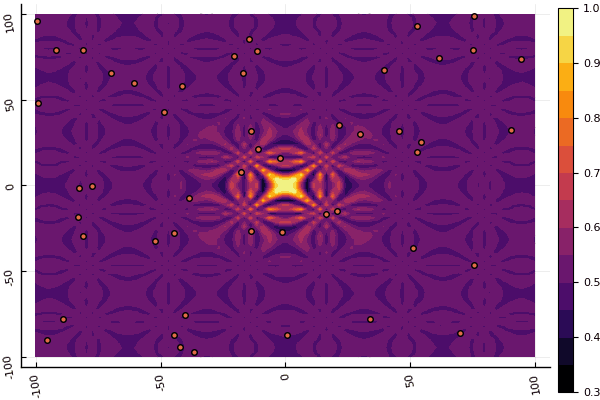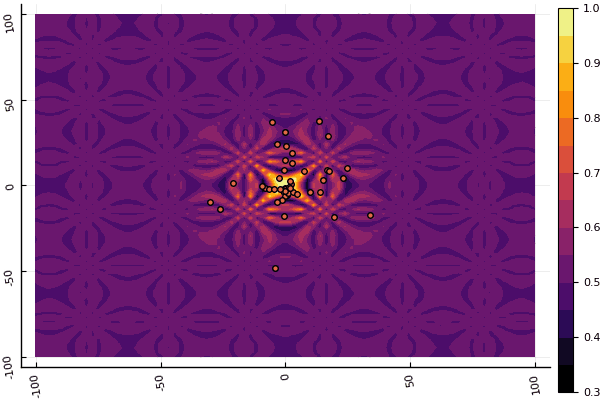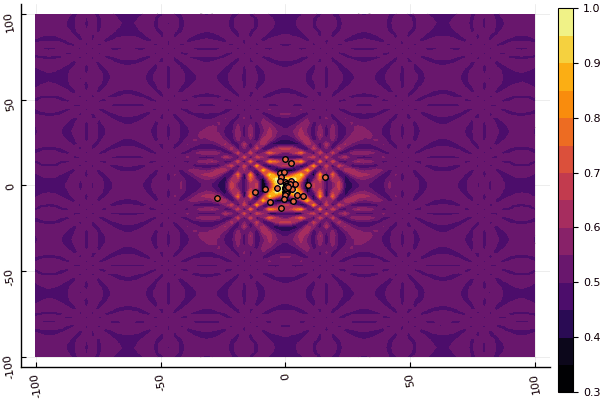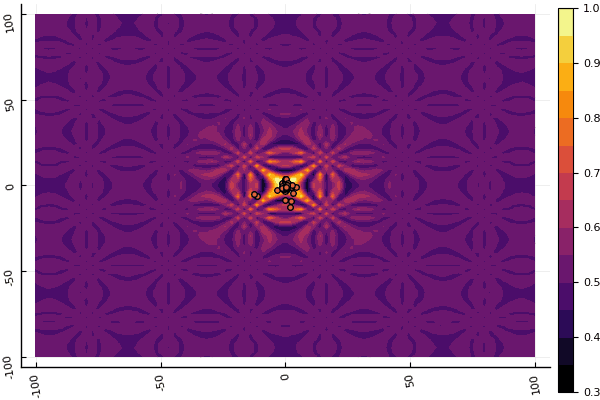
O que realmente deprime é mexer com parâmetros e um elemento de aleatoriedade: se não uma partícula voa perto do mínimo global, então tudo isso pode cair no local:

 fun = rastrigin mdpso(mdpso(C1 = [0.1 0.1], C2 = [1 1], Ac = [0.08 0.08], lover = low, upper = up, ages = 30)) 

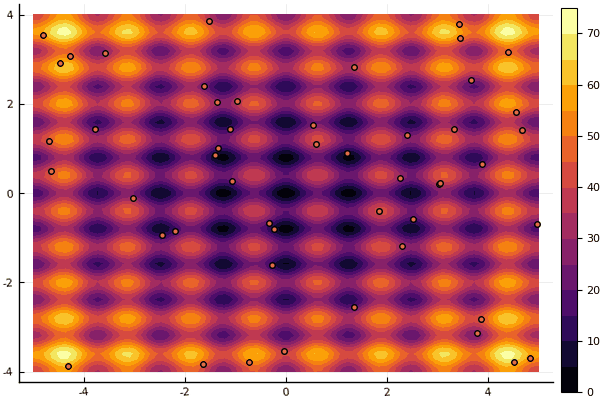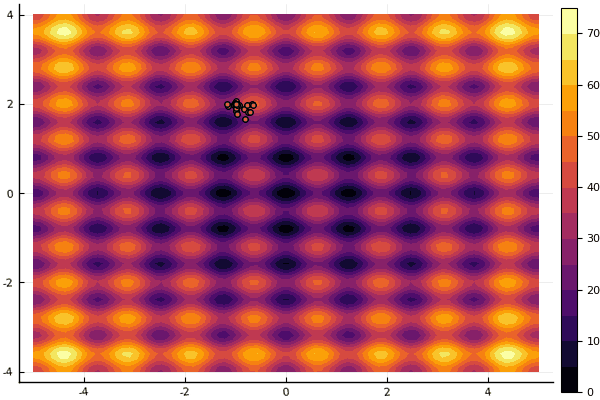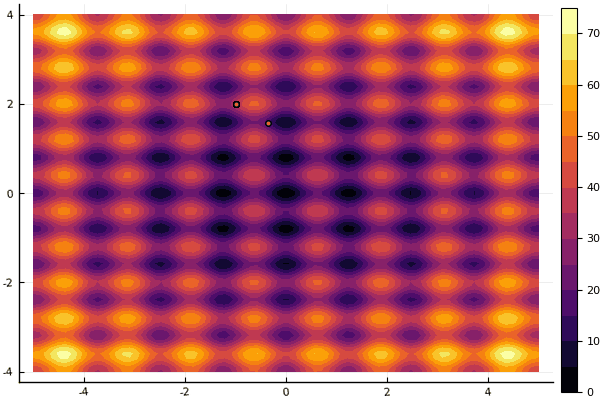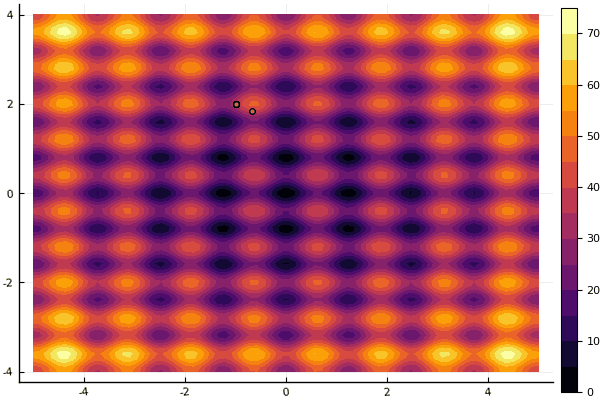
Sim e velho não muito o bom Rosenbrock ainda não permite se compreender:

 fun = rosenbrok mdpso(C1 = [1.7 1.7], C2 = [1.5 1.5], Ac = [0.15 0.15], lover = low, upper = up, ages = 20, nparts = 50) ... Age № 20 xbest: 0.37796421341886866 0.12799160066705667 Fmin: 0.409026370833564 

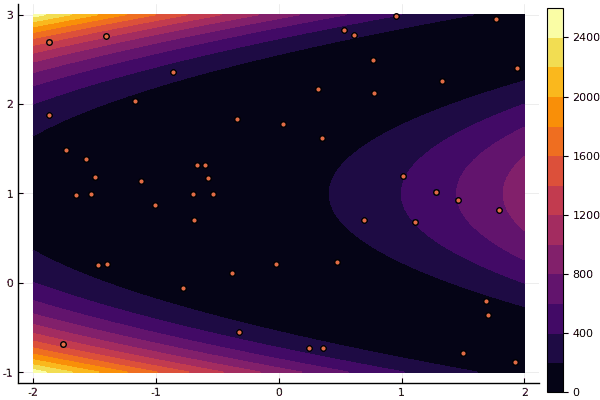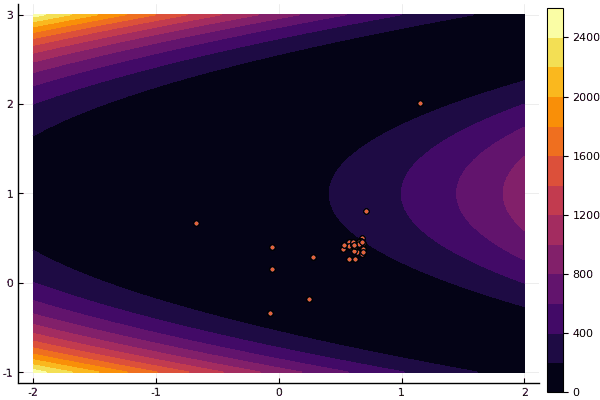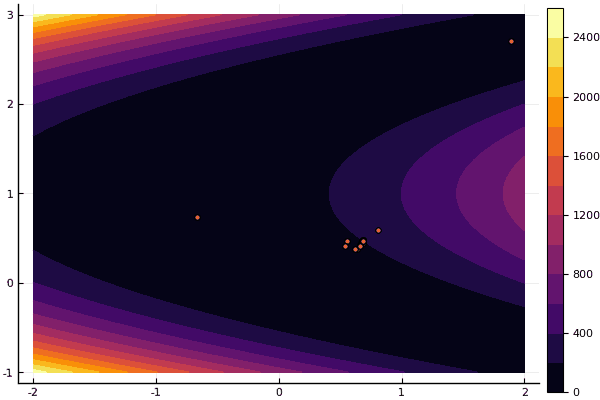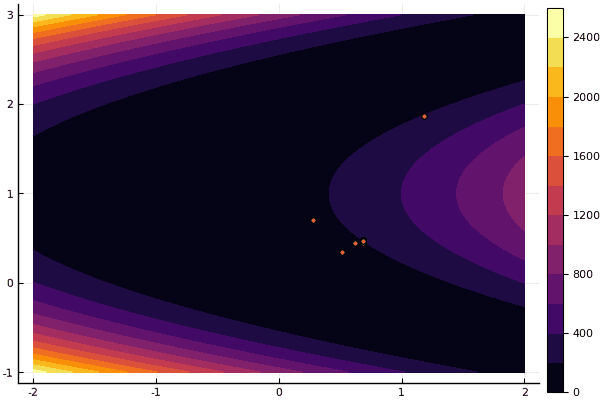
Mas, como eu disse anteriormente, você pode usar o FDM para procurar uma boa aproximação ao mínimo global e especificar, por exemplo, Nelder-Mead:

 vecl(x) = sqrt( sum(u -> u*u, x) ) function sortcoord(Mx) N = size(Mx,2) f = [fun(Mx[:,i]) for i in 1:N] #     Mx[:, sortperm(f)] end function normx(Mx) m = size(Mx,2) D = zeros(m-1,m) for i = 1:m, j = i+1:m D[i,j] = vecl(Mx[:,i] - Mx[:,j]) #     end D sqrt(maximum(D)) end function ofNelderMid(; ndimes = 2, ε = 1e-4, fit = [.1, .1], low = [-1 -1], up = [1 1]) k = 0 N = ndimes Xx = zeros(N, N+1) for i = 1:N+1 Xx[:,i] = fit end for i = 1:N Xx[i,i] += 0.5*vecl(fit) + ε end p = normx(Xx) while p > ε k += 1 Xx = sortcoord(Xx) Xo = [ sum(Xx[i,1:N])/N for i = 1:N ] #  - i-  Ro = 2Xo - Xx[:,N+1] FR = fun(Ro) if FR > fun(Xx[:,N+1]) for i = 2:N+1 Xx[:,i] = 0.5(Xx[:,1] + Xx[:,i]) end else if FR < fun(Xx[:,1]) Eo = Xo + 2(Xo - Xx[:,N+1]) if FR > fun(Eo) Xx[:,N+1] = Eo else Xx[:,N+1] = Ro end else if FR <= fun(Xx[:,N]) Xx[:,N+1] = Ro else Co = Xo + 0.5(Xo - Xx[:,N+1]) if FR > fun(Co) Xx[:,N+1] = Co else Xx[:,N+1] = Ro end end end end println(k, " ", p, " ", Xx[:,1]) p = normx(Xx) end #while fit = Xx[:,1] end 

 ofNelderMid(fit = [0.37796 0.127992]) ... 92 0.00022610400555036366 [1.0, 1.0] 93 0.00015987967588703512 [1.0, 1.0] 94 0.00011305200343052599 [1.0, 1.0] 2-element Array{Float64,1}: 0.9999999996645973 0.9999999995466575 

Para o MFC clássico, nem tudo é claro com o critério de parada: o melhor ponto pode manter a posição de várias épocas, as distâncias entre algumas partículas também não podem mudar por muito tempo. Portanto, um limite para o número de eras é usado. Para aumentar as chances de encontrar um mínimo global, é necessário aumentar o número de partículas e épocas, o que é muito caro em termos de memória e, além disso, de tempo (sem brincadeira, 50 chamadas da função objetivo para cada dimensão em cada iteração).

Moral

• Se você não quiser ou não puder usar métodos complexos e modernos, poderá usar composições de métodos mais simples
• Muitas vezes, para um problema, existe um método estreitamente afiado (por exemplo, para funções de ravina)
• É aconselhável ter vários MOs diferentes à mão para uma comparação consistente.
• Nem sempre é possível colocar sua tarefa no método e obter a resposta certa imediatamente - você deve dedicar algum tempo pesquisando, variando os parâmetros; se não conseguir visualizar o alívio, deve pelo menos imprimir cálculos intermediários para rastrear a convergência.

Por hoje é tudo, obrigado por sua atenção e desejo a todos uma boa otimização!