As provas / argumentos de conhecimento zero são uma tecnologia criptográfica emergente que promete nos aproximar do Santo Graal da blockchain: fornecendo privacidade e auditabilidade de dados.
Os aplicativos potenciais para conhecimento zero incluem, entre outros:
Outra aplicação para provas de conhecimento nulo está ajudando as blockchains a
escalar . Os ZKPs permitem a "compactação" de cálculos para transações de blockchain sem sacrificar a segurança.
Neste artigo, descrevemos como o conhecimento zero (especificamente, Bulletproofs ) pode ser aplicado para criar um serviço focado na privacidade usando a plataforma Exonum da Bitfury.
Análise situacional
É possível alcançar
algum nível de privacidade de dados em aplicativos blockchain usando a abordagem "walled garden", onde os dados estão ocultos porque o acesso a eles é restrito com a ajuda de firewalls, controle de acesso baseado em função,
fossos e outras medidas de segurança de perímetro . Os dados confidenciais na blockchain podem ser criptografados (talvez, com um esquema de criptografia de chave pública, com as chaves públicas relevantes gerenciadas pela mesma blockchain) e / ou armazenados fora da blockchain (nesse caso, a blockchain armazena apenas impressões digitais de hash de os dados). Essa abordagem é usada em muitas estruturas de contabilidade distribuída autorizadas.
No entanto, as desvantagens da abordagem do "jardim murado" estão se tornando cada vez mais aparentes. Para ser franco, a abordagem é antitética a um dos principais pontos de venda da blockchain - a auditabilidade. Se os dados no blockchain não puderem ser auditados consultando a lógica de contrato inteligente, o blockchain se tornará um serviço de
carimbo de data / hora vinculado glorificado. O fato de haver alguns dados no blockchain não significa mais que esses dados são válidos de acordo com as regras de contrato inteligentes. A segunda grande desvantagem da abordagem do jardim murado é que ela não escala. O CTO da R3, Richard Brown, por exemplo,
comparou adequadamente o modelo de privacidade de sua solução aos canais Slack - é difícil adicionar ou remover com segurança participantes do jardim, ainda mais quando não há expectativas anteriores quanto ao número e identidades desses participantes.
É aqui que o
conhecimento zero pode ser valioso. Por design, provas e argumentos de conhecimento zero provam convincentemente uma afirmação sobre dados privados sem revelar nada sobre os dados, exceto a comprovação. É fácil tornar as provas de zero conhecimento
universalmente verificáveis, sem sacrificar a privacidade! ² Esse recurso é exatamente o necessário para criar um sistema que preserva a privacidade e auditável ao mesmo tempo.
Nossa pesquisa
Para demonstrar o uso de provas de conhecimento nulo, vamos construir um serviço de criptomoeda com funcionalidade semelhante aos serviços de tutorial na
documentação do
Exonum . O serviço possibilita o registro de usuários e carteiras (fornecendo um saldo inicial de tokens como recompensa) e a transferência de tokens entre as partes registradas. Todas as transações são autenticadas com a ajuda de um sistema de criptografia de assinatura digital, Ed25519, que é incorporado aos serviços da Exonum. Não ocultamos as identidades das partes envolvidas na transação (ou seja, suas chaves públicas), mas ocultamos o número de tokens que estão sendo negociados e o saldo de cada conta no sistema. Também discutimos como poderíamos melhorar o serviço para ocultar as entidades de transação no final do artigo.
O serviço é totalmente aberto e pode ser acessado
aqui .
Fundo de criptografia
Para entender como o serviço funciona, primeiro precisamos nos apresentar à primitiva criptografia básica subjacente ao Bulletproofs - um conceito chamado
compromissos de Pedersen . Um esquema de confirmação criptográfica é um pouco como uma função de hash: alguém insere dados secretos (a abertura) e obtém a saída que é irreconhecível codificada (a confirmação). Pode-se então revelar a abertura para provar que o valor comprometido corresponde a ele.
A diferença com as funções hash é que, além de
vinculativo (ninguém pode conceber duas aberturas diferentes produzindo o mesmo compromisso), também se espera que um esquema de compromisso esteja
oculto (é impossível reverter o esquema e produzir uma abertura com um compromisso). Uma função de hash está oculta se sua entrada é distribuída uniformemente em todo o espaço de entrada, mas essa suposição frequentemente não se aplica a compromissos (na verdade, deve ser possível confirmar com um valor de um conjunto muito pequeno, como Booleano). Assim, a abertura contém, além da carga útil, o
fator ofuscante que torna (pelo menos estatisticamente) improvável adivinhar a carga útil dada o compromisso.
O esquema de compromisso de Pedersen usa um
grupo de primeira ordem , no qual se acredita que o
problema do logaritmo discreto (DLP) seja difícil, junto com dois geradores,
G e
H. G e
H devem ser escolhidos de maneira que a relação discreta entre eles seja desconhecida; em outras palavras, ninguém sabe
k tal que
H = kG .³ A abertura é um par
(x, r) , onde
x é o valor comprometido
er é o fator de cegamento; ambos são escalares de grupo (essencialmente, números inteiros com "estouro" semelhantes aos tipos inteiros finitos usados na maioria das linguagens de programação). O compromisso é calculado como
Comm (x; r) = xG + rH . Pode-se provar que, se o DLP no grupo é difícil, o compromisso de Pedersen é vinculativo em termos computacionais e perfeitamente oculto.⁴
A propriedade crucial para os compromissos de Pedersen é que eles são aditivos: a soma (ou diferença) de 2 compromissos é um compromisso com a soma (ou diferença) dos valores comprometidos. De fato,
C1 = x1 G + r1 H; C2 = x2 G + r2 H => C1 + C2 = (x1 + x2) G + (r1 + r2) H = Comm(x1 + x2; r1 + r2).
Não incluímos os detalhes aqui sobre como as provas de balas são construídas e verificadas, mas mais informações podem ser encontradas nos seguintes recursos - [
1 ] e [
2 ]. Basta observar que o limite superior do intervalo
M é assumido como forma
2 ^ (2 ^ n) , o que leva à construção de prova mais eficiente.
Construindo um serviço
Com o nosso conhecimento, podemos ocultar com segurança os saldos das contas e transferir valores com a ajuda dos compromissos da Pedersen. Usando provas de alcance, podemos provar / verificar se uma transferência está correta:
- O valor transferido é positivo
- O remetente tem saldo suficiente em sua conta.
Para a primeira prova, assumimos o compromisso com o valor da transferência,
C_a (está diretamente presente na transação de transferência) e verificamos se o valor confirmado em
C_a-Comm (1; 0) está no intervalo
[0, M) . De fato, isso é equivalente a provar que
C_a corresponde a um valor no intervalo
[1, M] . O remetente pode apresentar essa prova, pois conhece o valor transferido
a .
Para a segunda prova, precisamos assumir o compromisso com o saldo atual do remetente,
C_s , e verificar se o valor comprometido em
C_s-C_a está no intervalo
[0, M) . Novamente, o remetente pode produzir essa prova, pois conhece a abertura para
C_s e
C_a .
Para aplicar a transferência ao estado blockchain,
subtraímos o compromisso de valor
C_a do compromisso de
saldo do remetente (como verificamos, ele não pode levar a um saldo negativo ou ao aumento do saldo do remetente) e, em seguida, adicionamos
C_a ao equilibrar compromisso.
Detalhes principais
É importante observar que existem algumas condições que podem tornar o serviço implementado mais complexo.
O receptor de uma transferência deve descobrir a abertura para
C_a de algum lugar; caso contrário, ele deixa de conhecer a abertura do seu equilíbrio e não pode mais fazer nada com a carteira. A abertura não está presente no texto simples da transação de transferência (que é o ponto inteiro).
Poderíamos assumir que o receptor obtém de forma confiável a abertura por meio de um canal fora da cadeia (por exemplo, enviado pelo remetente via Telegram), mas esse não é um cenário ilustrativo. Então, em vez disso, criptografamos a abertura usando criptografia de chave pública de duas partes com base na troca de chaves Diffie-Hellman (a libsodium chama esse tipo de
caixa de criptografia). Para o benefício adicional, as chaves Curve25519 necessárias para a rotina da
caixa podem ser convertidas das chaves Ed25519, para que possamos continuar usando um único par de chaves para cada usuário, em vez de introduzir chaves de criptografia separadas.⁵

Depois de introduzirmos a criptografia, não podemos mais aplicar a transferência atomicamente. De fato, o remetente pode fornecer lixo de maneira maliciosa ou involuntária, em vez da criptografia de abertura, e a lógica da blockchain não será capaz de dizer que esse é o caso.⁶ Assim, solicitamos que o destinatário aceite explicitamente a transferência por meio de uma transação separada.
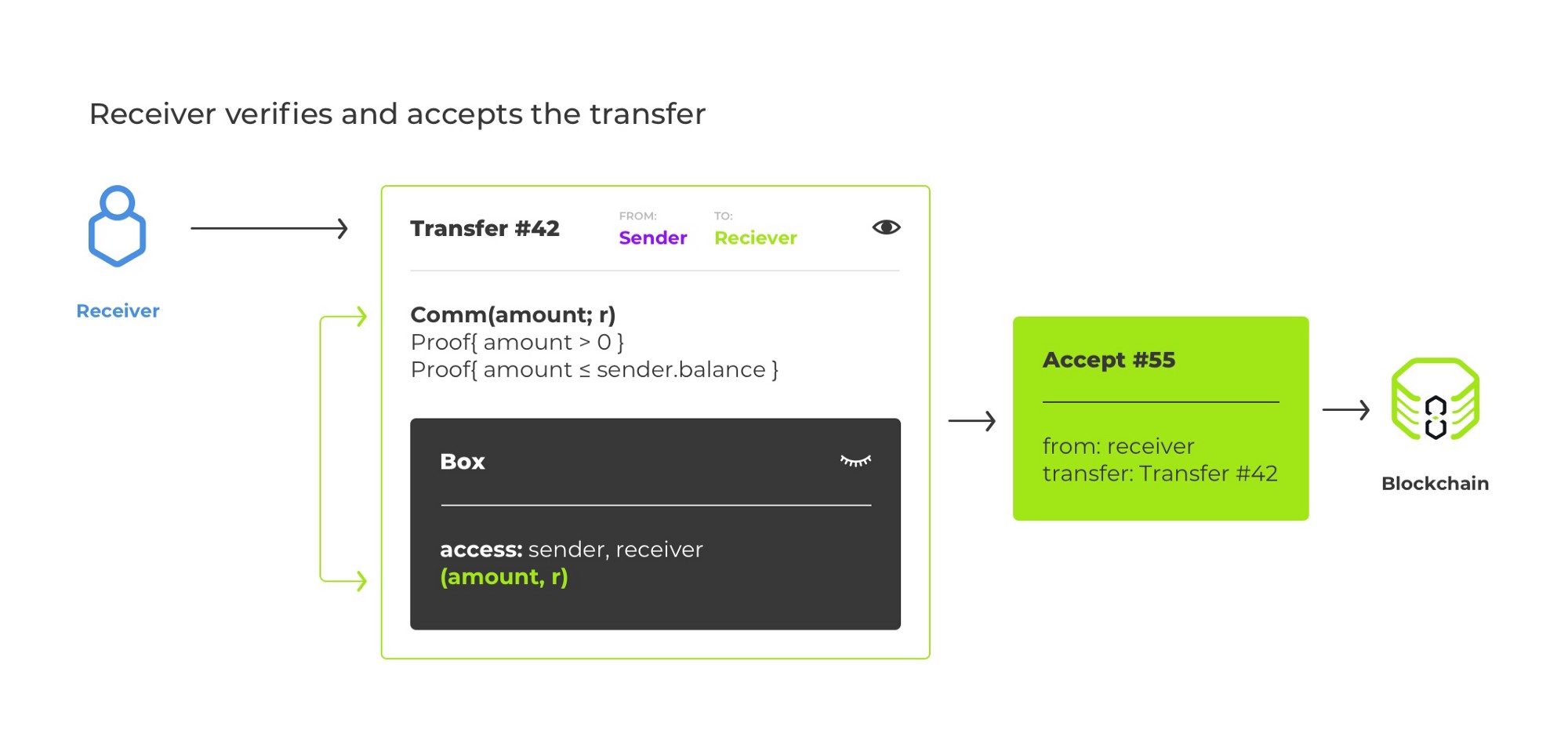
Antes de uma transferência ser aceita, ela modifica o compromisso de saldo do remetente (caso contrário, permitiríamos gastos duplos!), Mas não o do destinatário.

Depois que a transação de aceitação é confirmada pela rede blockchain, o saldo do receptor é atualizado e a transferência é concluída.

Para evitar conflitos, uma transferência especifica um atraso de bloqueio de tempo (na altura relativa da blockchain, no
CSV do Bitcoin) para o receptor sinalizar aceitação. Se o tempo limite expirar, a transferência será automaticamente reembolsada ao remetente (a Exonum permite isso através do gancho
Service :: beforeCommit () ).
Outra questão é mais complexa. Para produzir a prova de um saldo suficiente, o remetente precisa conhecer seu saldo atual, o que nem sempre pode ser o caso. Uma transação ou reembolso perdido de aceitação pode aumentar o saldo do remetente sem querer para ele; nesse caso, a transferência falhará na verificação e o remetente ficará razoavelmente frustrado.
Para aliviar esse problema, permitimos que as transferências façam referência ao que o remetente acha que é seu estado atual da carteira (mais precisamente, a referência toma forma do número de eventos que alteram o saldo da conta - transferências e reembolsos). Ao verificar a prova de um saldo suficiente, usamos o estado referenciado para obter o compromisso de saldo do remetente. Além disso, verificamos que nenhuma transferência de saída ocorreu desde o estado referenciado. Se for esse o caso, podemos ter certeza de que, se subtrairmos o valor da transferência do saldo
atual do remetente, teremos um valor não negativo. De fato, os eventos no histórico da conta após o ponto de referência (transferências e reembolsos recebidos) só podem aumentar o saldo! ⁷
Com os pontos de referência no lugar, o remetente ainda está um pouco restrito; ele / ela não deve ter transferências pendentes ao criar uma nova transferência. Ainda assim, essa restrição é muito menos limitadora do que a exigência de conhecer o estado da conta no momento da transferência; fundamentalmente, tornamos o remetente dependente do que
ele fez anteriormente, mas não das ações dos outros.
Implementação
Utilizamos uma biblioteca à prova de balas, escrita em puro
Rust , que chegou recentemente ao
estágio de pré-lançamento . Como a plataforma Exonum é escrita em Rust, ela se integra perfeitamente à biblioteca. Como um bônus, diferente da versão das provas de balas descrita no whitepaper original (que está sendo desenvolvido em
C e usa a curva elíptica secp256k1 do Bitcoin), a biblioteca que usamos é baseada no Curve25519, que já é usado no Exonum como o principal componente do Sistema de criptografia de assinatura digital Ed25519.
A implementação do serviço com base na descrição acima é bastante direta. A parte mais difícil foi a construção de provas de Merkle que autenticam as informações retornadas ao usuário para que ele não precise confiar cegamente nos nós do Exonum com os quais ele se comunica. Melhorar a experiência dos desenvolvedores de serviços nesse sentido é um dos principais objetivos da
versão Exonum 1.0 .
Próximas etapas
O serviço que criamos não oculta as identidades do remetente e do destinatário das transferências, o que é uma grande limitação para aplicativos do mundo real. Felizmente, existem maneiras de resolver esse problema.
A técnica genérica usada no
zCash (mas principalmente aplicável a outros casos de uso, como o
Ethereum ) baseia-se na criação de uma
árvore Merkle do estado do sistema. Por exemplo, o zCash cria a
árvore de confirmação de
notas , que é aproximadamente equivalente aos resultados de transações já criados no Bitcoin. As provas de conhecimento zero, em seguida, abrangem caminhos de autenticação (também conhecidos como ramos de Merkle) nessa árvore, revelam algo sobre um elemento da árvore sem revelar a qual elemento é referido. A desvantagem dessa abordagem é que as funções de hash criptográfico usadas para construir árvores Merkle são difíceis de transferir para o domínio de conhecimento zero; as provas resultantes se tornam computacionalmente caras - uma única prova pode levar segundos ou até minutos para criar. A busca por mais funções hash criptográficas “compatíveis com o ZKP” é a área da pesquisa ativa.
Se admitirmos restrições adicionais, pode haver uma solução mais fácil. Por exemplo, um artigo recente de
Narula et al . descreve um sistema com um número conhecido limitado e a priori de participantes, que pode realizar transações entre si sem revelar participantes ou valores transferidos para qualquer transação. (Pense em uma rede blockchain focada na privacidade para transferências interbancárias.)
Em uma nota mais prosaica, provavelmente existem muitas melhorias técnicas que o serviço desenvolvido pode usufruir: mais cobertura de teste, separação de chaves de assinatura e criptografia, benchmarking etc. Uma grande melhoria no serviço UX seria permitir a ordem determinística de transações originárias do mesmo usuário, que planejamos resolver pouco tempo depois do lançamento do Exonum 1.0.
Conclusão
Descrevemos como construir um criptografado baseado em conta com forte privacidade, habilitado por provas de zero conhecimento (especificamente, à prova de balas). A lógica do token foi implementada como um serviço Exonum. Embora atualmente o serviço seja apenas uma prova de conceito, ele mostra como a plataforma Exonum pode ser usada para criar sobre primitivas criptográficas complexas com sobrecarga muito baixa imposta pelo ambiente de execução.
- Há uma intrincada distinção entre provas e argumentos, sobre os quais não entraremos aqui. Por uma questão de simplicidade, vamos nos referir a todas as construções de conhecimento zero neste artigo como provas de conhecimento zero, mesmo que isso nem sempre seja correto do ponto de vista teórico.
- Isso pode ser conseguido através de uma técnica muito geral conhecida como transformação Fiat - Shamir , que converte um protocolo de prova interativo em um não interativo e universalmente verificável. Sacrificando o rigor científico mais uma vez, não esclareceremos explicitamente que as provas de conhecimento zero que usamos são não interativas.
- Geralmente, os geradores são escolhidos com o método "nada na manga". Por exemplo, G pode fazer parte da especificação do grupo para uso na criptografia de chave pública, e H é derivado de G através de uma função hash: H ~ hash (G) .
- O último significa que mesmo um adversário com poder computacional infinito não pode deduzir com o que o compromisso se compromete; de fato, se o DLP no grupo for quebrado, todo compromisso poderá ser aberto para qualquer valor possível.
- Esta é parcialmente uma decisão de prova de conceito; em geral, reutilizar chaves para diferentes propósitos é uma má idéia.
- É teoricamente possível fornecer uma prova de zero conhecimento para o valor criptografado equivalente ao saldo confirmado; no entanto, aumentaria proibitivamente a complexidade do sistema.
- É importante mencionar que algumas transferências que quebram a regra "sem transferências de saída desde o estado de referência" ainda podem estar corretas; simplesmente não temos como verificar isso.