Se você não leu meu primeiro artigo sobre o assunto, recomendo que você comece com
ele .
Como mencionei uma certa atitude, embora muito indireta, em relação aos matemáticos financeiros, deixe-me desenvolver o tópico ao ponto do absurdo com base em como ele é desenvolvido no Risk Analytics. Ao calcular o preço de uma opção, eles geralmente consideram a sensibilidade desse preço a um conjunto de parâmetros. Por exemplo, como o preço da opção mudará quando o preço da ação para a qual a opção é emitida mudar, ou quando a volatilidade do preço da ação ou a taxa do Banco Central mudar, etc.
Podemos estar interessados em como a probabilidade de ganhar um jogo muda quando a probabilidade de ganhar um ponto muda. De fato, queremos calcular a derivada do primeiro ao segundo. A abordagem mais simples é avaliá-la a olho no gráfico. Pode-se observar que o máximo é alcançado em uma situação de 50:50. Se as chances de ganhar um ponto mudar de 0,45 para 0,55, a probabilidade de ganhar badminton aumenta de 0,26 para 0,74, ou seja, 0,48. Uma estimativa aproximada fornece um derivado na região de 5. Ou seja, se você crescer até 0,51 (ou seja, 51%) com chances iguais, o aumento na probabilidade de ganhar o jogo será em torno de 0,05 (ou 5%). Da mesma forma, você pode calcular a derivada em qualquer outro ponto do gráfico.
Em finanças, geralmente é usada a abordagem “bump and run”, ou seja, eles alteram o parâmetro por uma pequena quantia e calculam o novo preço da opção e o derivativo. Tendo agido de maneira semelhante, cito os dados exatos no gráfico (tomei a alteração em uma porcentagem, um pouco rude, mas aceitável nessa situação). Para maior clareza, ele acrescentou jogos de 5 e 31 pontos. A propósito, fotografar em biatlo pode ser considerado uma festa de até 5. Isso não é uma analogia absoluta, já que o número total de fotos é fixo. Mas os métodos de solução são quase os mesmos.
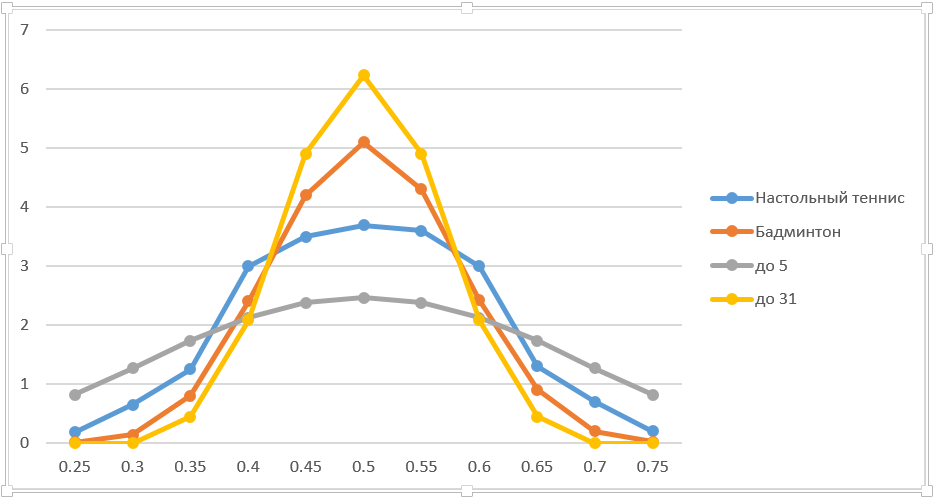
Obviamente, quanto maior o lote, maior a derivada em 50:50. Se a duração da festa tende ao infinito, a vitória de um jogador com uma vantagem mínima é praticamente garantida. A largura da curva diminui de acordo. Em geral, as conclusões são bastante óbvias.
Você pode calcular a sensibilidade à descarga acidental de um ponto. Por exemplo, alimente a rede. Quanto um deslize afeta o resultado do jogo? De fato, isso é uma redução na pontuação vencedora do oponente em um ponto. O gráfico abaixo reflete essa situação. Naturalmente, no tênis de mesa, é mais crítico perder um ponto do que no badminton. Com forças iguais, a probabilidade do resultado do jogo cai o máximo possível - de 0,5 para 0,41. Preste atenção à assimetria das curvas (diferente da maioria das outras). Isso não é coincidência. O fato é que o saldo muda de 50:50 para uma maior probabilidade de ganhar um ponto, já que um ponto perdido piora as chances de um jogador.
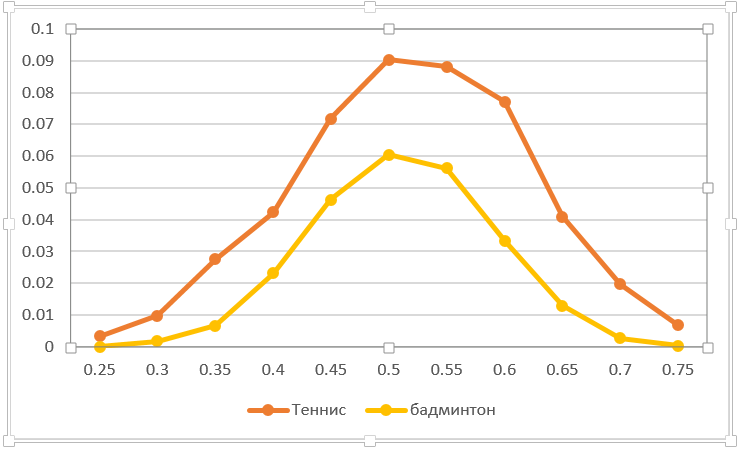
Vamos colocar outra experiência interessante. Imagine que um dos jogadores possa se concentrar e jogar 3 pontos acima da média (p1 + delta). Suponha que, depois disso, o alinhamento retorne ao original (para a média esperada sem levar em consideração o "aumento da força"). É claro que a probabilidade de ganhar aumentará. A questão é: importa quando se concentrar - no início ou no final do jogo? Proponho fazer uma suposição antes de ler mais.
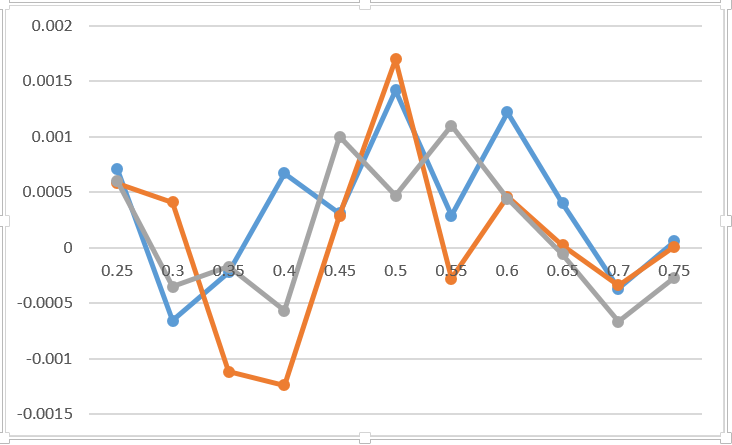
Assim, como mostra o experimento, não há absolutamente nenhuma diferença quando exatamente se concentrar (os fatores do plano moral não são levados em consideração). O gráfico mostra a diferença entre a probabilidade de ganhar o jogo em caso de concentração em 3 locais diferentes do jogo em comparação com a concentração nos 3 primeiros pontos. Penso que este gráfico reflete o erro de Monte Carlo e nada mais. Acrescentei 0,2 ao resultado do empate de pontos para o primeiro jogador em três empates. Nem indico no gráfico qual linha corresponde a qual opção. Definitivamente não muda nada. O único conselho valioso sobre esse assunto é se preparar antes que seja tarde demais.
Agora vamos considerar o que acontecerá se um dos jogadores tiver estabilidade. Nervos são nervos, um jogo responsável acontece. Suponha que, em média, ele ganhe a mesma porcentagem de pontos, mas ao desenhar um ponto específico, essa porcentagem flutua. Por exemplo, metade dos pontos são jogados com probabilidade p1 + delta, e a outra metade com p1-delta. Nesse caso, a média p1 permanece a original, a perda de + delta ou –delta ocorre aleatoriamente com uma probabilidade de 0,5. Isso afetará de alguma forma o resultado do jogo? Como minhas experiências com a ajuda de Monte Carlo mostraram, a diferença praticamente não é encontrada. De fato, adicionando ou subtraindo uma certa quantia, embora aleatoriamente, continuamos com a mesma probabilidade média de ganhar um ponto. A sugestão sugere que a curva de distribuição não afeta o resultado do jogo, mas apenas a média, mas eu não vou assumir isso por mim mesma. Aqui você tem que pensar.
Eu também gostaria de derivar uma equação diferencial, como Black Scholes em finanças, para completar a associação. Identifique derivadas significativas, zere o componente aleatório ... Também precisamos lidar com a discrição. Talvez eu deixe isso para matemáticos financeiros reais.