🧞 🚾 📕 Julia e otimização 👨🏿‍🤝‍👨🏽 ⏏️ 🔗

É hora de considerar pacotes que fornecem métodos para resolver problemas de otimização. Muitos problemas podem ser reduzidos para encontrar o mínimo de alguma função; portanto, você deve ter alguns ou dois solucionadores no arsenal e, ainda mais, um pacote inteiro.

Entrada

A linguagem Julia continua a ganhar popularidade . Em https://juliacomputing.com, você pode ver por que astrônomos, robôs e financiadores escolhem esse idioma. Em https://academy.juliabox.com, você pode iniciar cursos gratuitos para aprender o idioma e usá-lo em qualquer tipo de aprendizado de máquina. Para aqueles que decidiram começar a aprender seriamente, aconselho assistir ao vídeo, ler artigos e clicar em laptops jupiter em https://julialang.org/learning/ ou, pelo menos, percorrer o hub de baixo para cima: haverá instalação, recursos e aplicativo para negócios urgente. Agora vamos às bibliotecas.

Blackboxoxptim

BlackBoxOptim - pacote de otimização global para Julia ( http://julialang.org/ ). Ele suporta problemas de otimização de uso múltiplo e de uso único e é focado em algoritmos (meta) heurísticos / estocásticos (DE, NES etc.) que NÃO exigem que a função otimizada seja diferenciável, diferentemente dos algoritmos determinísticos mais tradicionais, frequentemente baseados em gradientes / diferenciabilidade. Ele também suporta computação paralela para acelerar a otimização de funções avaliadas lentamente.

Baixe e conecte a biblioteca

]add BlackBoxOptim using BlackBoxOptim

Defina a função Rosenbrock:

 f(x) = (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2

Estamos procurando um mínimo no intervalo (-5; 5) para cada coordenada para um problema bidimensional:

 res = bboptimize(f; SearchRange = (-5.0, 5.0), NumDimensions = 2)

Qual a resposta a seguir:

 Starting optimization with optimizer DiffEvoOpt{FitPopulation{Float64},RadiusLimitedSelector,BlackBoxOptim.AdaptiveDiffEvoRandBin{3},RandomBound{RangePerDimSearchSpace}} 0.00 secs, 0 evals, 0 steps Optimization stopped after 10001 steps and 0.12400007247924805 seconds Termination reason: Max number of steps (10000) reached Steps per second = 80653.17866385692 Function evals per second = 81628.98454510146 Improvements/step = 0.2087 Total function evaluations = 10122 Best candidate found: [1.0, 1.0] Fitness: 0.000000000

e muitos dados ilegíveis, mas foi encontrado um mínimo. Como o estocástico é usado, as chamadas de função serão um pouco demais; portanto, para tarefas multidimensionais, é melhor usar a seleção de métodos

 function rosenbrock(x) return( sum( 100*( x[2:end] - x[1:end-1].^2 ).^2 + ( x[1:end-1] - 1 ).^2 ) ) end res = compare_optimizers(rosenbrock; SearchRange = (-5.0, 5.0), NumDimensions = 30, MaxTime = 3.0);

Convexo

Convexo é o pacote de Programação Convexa Disciplinada de Julia (programação convexa disciplinar?). O Convex.jl pode resolver programas lineares, programas lineares inteiros mistos e programas convexos compatíveis com DCP usando vários solucionadores, incluindo Mosek, Gurobi, ECOS, SCS e GLPK, através da interface MathProgBase. Também suporta otimização com variáveis e coeficientes complexos.

 using Pkg #      Pkg.add("Convex") Pkg.add("SCS")

Existem muitos exemplos no site: Tomografia (o processo de restaurar a distribuição de densidade por integrais dadas sobre as áreas de distribuição. Por exemplo, você pode trabalhar com tomografia em imagens em preto e branco), maximizando a entropia, a regressão logística, a programação linear, etc.

Por exemplo, você precisa satisfazer as condições:

\ begin {array} {ll} \ mbox {satisfazer} & \ | x \ | _2 \ leq 100 \\ & e ^ {x_1} \ leq 5 \\ & x_2 \ geq 7 \\ & \ sqrt {x_3 x_4} \ geq x_2 \ end {array}

$\ begin {array} {ll} \ mbox {satisfazer} & \ | x \ | _2 \ leq 100 \\ & e ^ {x_1} \ leq 5 \\ & x_2 \ geq 7 \\ & \ sqrt {x_3 x_4} \ geq x_2 \ end {array}$

 using Convex, SCS, LinearAlgebra x = Variable(4) p = satisfy(norm(x) <= 100, exp(x[1]) <= 5, x[2] >= 7, geomean(x[3], x[4]) >= x[2]) solve!(p, SCSSolver(verbose=0)) println(p.status) x.value

Vai dar uma resposta

 Optimal 4×1 Array{Float64,2}: 0.0 8.554892320716046 15.329934133156783 15.329934133156783

Jump

JuMP é uma linguagem de otimização matemática específica de domínio incorporada à Julia. Atualmente, ele suporta vários solucionadores abertos e comerciais (Artelys Knitro, BARON, Bonmin, Cbc, Clp, Couenne, CPLEX, ECOS, FICO Xpress, GLPK, Gurobi, Ipopt, MOSEK, NLopt, SCS).

O JuMP facilita a identificação e a solução de problemas de otimização sem o conhecimento de especialistas, mas, ao mesmo tempo, permite que os especialistas implementem métodos algorítmicos avançados, como o uso de partidas "quentes" efetivas na programação linear ou o uso de retornos de chamada para interagir com solucionadores de ramificações e limites. O JuMP também é rápido - o benchmarking mostrou que ele pode lidar com cálculos em velocidades semelhantes às ferramentas comerciais especializadas, como a AMPL, mantendo a expressividade de uma linguagem de programação universal de alto nível. O JuMP pode ser facilmente integrado a fluxos de trabalho complexos, incluindo simulações e servidores da web.

Essa ferramenta permite lidar com tarefas como:

LP = programação linear
QP = Programação Quadrática
SOCP = programação cônica de segunda ordem (incluindo problemas com restrições quadráticas convexas e / ou finalidade)
MILP = Programação Linear Inteira Mista
PNL = Programação Não Linear
MINLP = programação não linear inteira mista
SDP = programação semi-definida
MISDP = programação semidefinida de número inteiro misto

A análise de seus recursos será suficiente para vários artigos, portanto, por enquanto, passemos ao seguinte:

Optim

Optim Existem muitos solucionadores disponíveis em fontes gratuitas e comerciais, e muitos já estão disponíveis para uso em Julia. Poucos deles estão escritos neste idioma. Em termos de desempenho, isso raramente é um problema, pois geralmente são escritos em Fortran ou C. No entanto, os solucionadores escritos diretamente em Julia têm algumas vantagens.

Ao escrever o software Julia (pacotes) para o qual algo precisa ser otimizado, o programador pode escrever seu próprio procedimento de otimização ou usar um dos muitos solucionadores disponíveis. Por exemplo, poderia ser algo do conjunto NLOpt. Isso significa adicionar uma dependência que não está escrita em Julia e você precisa fazer mais suposições sobre o ambiente em que o usuário está localizado. O usuário possui compiladores adequados? Posso usar o código GPL em um projeto?

Também é verdade que usar um solucionador escrito em C ou Fortran torna impossível usar uma das principais vantagens de Julia: despacho múltiplo. Como o Optim foi totalmente escrito em Julia, atualmente podemos usar um sistema de despacho para facilitar o uso de predefinições personalizadas. Um recurso planejado nessa direção é permitir uma seleção orientada pelo usuário de solucionadores para os vários estágios do algoritmo, com base inteiramente no envio, e não nos recursos predefinidos escolhidos pelos desenvolvedores do Optim.

Um pacote na Julia também significa que o Optim tem acesso às funções de diferenciação automática por meio de pacotes no JuliaDiff .

Guia

Prossiga:

 ]add Optim using Optim #   f(x) = (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2 x0 = [0.0, 0.0] optimize(f, x0)

Recebemos uma resposta com um relatório conveniente:

 Results of Optimization Algorithm * Algorithm: Nelder-Mead #   * Starting Point: [0.0,0.0] * Minimizer: [0.9999634355313174,0.9999315506115275] * Minimum: 3.525527e-09 * Iterations: 60 * Convergence: true * √(Σ(yᵢ-ȳ)²)/n < 1.0e-08: true * Reached Maximum Number of Iterations: false * Objective Calls: 118

E compare com o meu Nelder Mead!

spoiler

O meu será mais lento :(

Escondido

 using BenchmarkTools @benchmark optimize(f, x0) BenchmarkTools.Trial: memory estimate: 11.00 KiB allocs estimate: 419 -------------- minimum time: 39.078 μs (0.00% GC) median time: 43.420 μs (0.00% GC) mean time: 53.024 μs (15.02% GC) maximum time: 59.992 ms (99.83% GC) -------------- samples: 10000 evals/sample: 1

No decorrer da verificação, também constatou que minha implementação não funcionará se você usar a aproximação inicial (0, 0). Como critério de parada, você pode usar o volume do simplex , mas eu uso a norma de uma matriz composta de vértices. Aqui você pode ler sobre a interpretação geométrica da norma. Nos dois casos, é obtida uma matriz de zeros - um caso especial de uma matriz degenerada; portanto, o método não executa nenhuma etapa. Você pode configurar a criação de um simplex inicial, por exemplo, definindo a distância de seus vértices da aproximação inicial (e não como a minha - metade do comprimento do vetor, fu, que pena ...), então a configuração do método será mais flexível ou verifique se todos os vértices não são sentou-se em um ponto:

  for i = 1:N+1 Xx[:,i] = fit end for i = 1:N Xx[i,i] += 0.5*vecl(fit) + ε end

Bem, sim, meu goraaazdo simplex é mais lento:

 ofNelderMid(fit = [0, 0.]) step= 118 7.7234e-5 f = 2.797-18 x = [1.0, 1.0] @benchmark ofNelderMid(fit = [0., 0.]) BenchmarkTools.Trial: memory estimate: 394.03 KiB allocs estimate: 6632 -------------- minimum time: 717.221 μs (0.00% GC) median time: 769.325 μs (0.00% GC) mean time: 854.644 μs (5.04% GC) maximum time: 50.429 ms (98.01% GC) -------------- samples: 5826 evals/sample: 1

Agora, mais um motivo para retornar ao pacote de estudos

Você pode escolher o método usado:

 optimize(f, x0, LBFGS()) Results of Optimization Algorithm * Algorithm: L-BFGS * Starting Point: [0.0,0.0] * Minimizer: [0.9999999926662504,0.9999999853325008] * Minimum: 5.378388e-17 * Iterations: 24 * Convergence: true * |x - x'| ≤ 0.0e+00: false |x - x'| = 4.54e-11 * |f(x) - f(x')| ≤ 0.0e+00 |f(x)|: false |f(x) - f(x')| = 5.30e-03 |f(x)| * |g(x)| ≤ 1.0e-08: true |g(x)| = 9.88e-14 * Stopped by an increasing objective: false * Reached Maximum Number of Iterations: false * Objective Calls: 67 * Gradient Calls: 67

e obtenha documentação detalhada e referências a ele

 ?LBFGS()

Você pode definir funções jacobianas e hessianas

 function g!(G, x) G[1] = -2.0 * (1.0 - x[1]) - 400.0 * (x[2] - x[1]^2) * x[1] G[2] = 200.0 * (x[2] - x[1]^2) end function h!(H, x) H[1, 1] = 2.0 - 400.0 * x[2] + 1200.0 * x[1]^2 H[1, 2] = -400.0 * x[1] H[2, 1] = -400.0 * x[1] H[2, 2] = 200.0 end optimize(f, g!, h!, x0) Results of Optimization Algorithm * Algorithm: Newtons Method * Starting Point: [0.0,0.0] * Minimizer: [0.9999999999999994,0.9999999999999989] * Minimum: 3.081488e-31 * Iterations: 14 * Convergence: true * |x - x'| ≤ 0.0e+00: false |x - x'| = 3.06e-09 * |f(x) - f(x')| ≤ 0.0e+00 |f(x)|: false |f(x) - f(x')| = 3.03e+13 |f(x)| * |g(x)| ≤ 1.0e-08: true |g(x)| = 1.11e-15 * Stopped by an increasing objective: false * Reached Maximum Number of Iterations: false * Objective Calls: 44 * Gradient Calls: 44 * Hessian Calls: 14

Aparentemente, elaborou automaticamente o método de Newton. E assim você pode definir a área de pesquisa e usar a descida do gradiente:

 lower = [1.25, -2.1] upper = [Inf, Inf] initial_x = [2.0, 2.0] inner_optimizer = GradientDescent() results = optimize(f, g!, lower, upper, initial_x, Fminbox(inner_optimizer)) Results of Optimization Algorithm * Algorithm: Fminbox with Gradient Descent * Starting Point: [2.0,2.0] * Minimizer: [1.2500000000000002,1.5625000000000004] * Minimum: 6.250000e-02 * Iterations: 8 * Convergence: true * |x - x'| ≤ 0.0e+00: true |x - x'| = 0.00e+00 * |f(x) - f(x')| ≤ 0.0e+00 |f(x)|: true |f(x) - f(x')| = 0.00e+00 |f(x)| * |g(x)| ≤ 1.0e-08: false |g(x)| = 5.00e-01 * Stopped by an increasing objective: false * Reached Maximum Number of Iterations: false * Objective Calls: 84382 * Gradient Calls: 84382

Bem, ou eu não sei, digamos que você queira resolver a equação

 f_univariate(x) = 2x^2+3x+1 optimize(f_univariate, -2.0, 1.0) Results of Optimization Algorithm * Algorithm: Brents Method * Search Interval: [-2.000000, 1.000000] * Minimizer: -7.500000e-01 * Minimum: -1.250000e-01 * Iterations: 7 * Convergence: max(|x - x_upper|, |x - x_lower|) <= 2*(1.5e-08*|x|+2.2e-16): true * Objective Function Calls: 8

e ele escolheu o método Brent .
Ou, com dados experimentais, você precisa otimizar os coeficientes do modelo

F (p_{1}, p_{2}, x) = p_{1} c o s (p_{2} x) + p_{2} s i n (p_{1} x)

$F (p_1, p_2, x) = p_1 \ cos (p_2x) + p_2 \ sin (p_1x)$

p_{1} = 1, p_{2} = 0, 2

$p_1 = 1, p_2 = 0,2$

 F(p, x) = p[1]*cos(p[2]*x) + p[2]*sin(p[1]*x) model(p) = sum( [ (F(p, xdata[i]) - ydata[i])^2 for i = 1:length(xdata)] ) xdata = [-2,-1.64,-1.33,-0.7,0,0.45,1.2,1.64,2.32,2.9] ydata = [0.699369,0.700462,0.695354,1.03905,1.97389,2.41143,1.91091,0.919576,-0.730975,-1.42001] res2 = optimize(model, [1.0, 0.2]) Results of Optimization Algorithm * Algorithm: Nelder-Mead * Starting Point: [1.0,0.2] * Minimizer: [1.8818299027162517,0.7002244825046421] * Minimum: 5.381270e-02 * Iterations: 34 * Convergence: true * √(Σ(yᵢ-ȳ)²)/n < 1.0e-08: true * Reached Maximum Number of Iterations: false * Objective Calls: 71

 P = Optim.minimizer(res2) Y = [ F(P, x) for x in xdata] using Plots plotly() plot(xdata, ydata) plot!(xdata, Y)

Bônus Crie sua função de teste

A ideia é usada no artigo de Khabrov . Você pode configurar cada mínimo local:

 """ https://habr.com/ru/post/349660/ :param n:   :param a:    ,   ,    /      :param c:    :param p:       :param b:    :return:  ,       ,          """ function feldbaum(x; n=5, a=[3 2; 4 3; 2 1; 4 5; .5 .5], c=[-1 2; 2 1; -3 2; -2 -2; 1.5 -2], p=[9 6; 1 1; 1.5 1.4; 1.2 1.3; 0.5 0.5], b=[0 1 3.2 2 4.6]) l = zeros(n) for i = 1:n res = 0 for j = 1:size(x,1) res += a[i,j] * abs(x[j] - c[i,j]) ^ p[i,j] end res += b[i] l[i] = res end minimum(l) end

E você pode deixar tudo à vontade do todo-poderoso aleatório

 n=10 m = 2 a = rand(0:0.1:6, n, m) c = rand(-2:0.1:2, n, m) p = rand(0:0.1:2, n, m) b = rand(0:0.1:8, n, m) function feldbaum(x) l = zeros(n) for i = 1:n res = 0 for j = 1:m res += a[i,j] * abs(x[j] - c[i,j]) ^ p[i,j] end res += b[i] l[i] = res end minimum(l) end

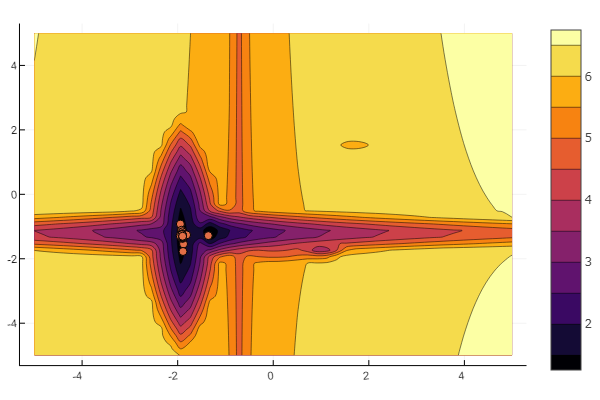
Mas, como você pode ver na imagem inicial, um enxame de partículas com esse alívio não é intimidador.

Isso deve ser feito. Como você pode ver, Julia possui um ambiente matemático bastante poderoso e moderno, que permite a realização de estudos numéricos complexos sem precisar de abstrações de programação de baixo nível. E esta é uma excelente ocasião para continuar estudando esse idioma.

Boa sorte a todos!