Neste artigo, apresento uma nova sequência quase aleatória de baixa divergência que fornece melhorias significativas em relação às seqüências modernas, como Sable, Niederreiter, etc.Figura 1. Comparação de várias seqüências quase aleatórias com baixa divergência. Observe que o proposto por mim R A sequência cria pontos distribuídos de maneira mais uniforme do que todos os outros métodos. Além disso, todos os outros métodos requerem seleção cuidadosa dos parâmetros básicos e, no caso de seleção incorreta, levam à degeneração (por exemplo, no canto superior direito)Tópicos abordados neste artigo- Sequências de baixa divergência em uma dimensão
- Métodos de baixa divergência em duas dimensões
- Distância da embalagem
- Conjuntos de baixa discrepância multiclasse
- Sequências quase aleatórias na superfície de uma esfera
- Mosaico plano quase-periódico
- Máscaras pontilhadas em computação gráfica
Há algum tempo, este post foi publicado na página inicial do Hacker News. Você pode ler a
discussão dele
lá .
Introdução: aleatória versus quase aleatória
Na Figura 1, você pode notar que, com uma amostragem aleatória simples e uniforme de um ponto dentro de um quadrado de unidade, é observado um acúmulo de pontos e também surgem áreas sem pontos (“ruído branco”). Uma
sequência quase aleatória de
baixa divergência é um método de construir pontos consecutivos (infinitos) de maneira determinística, o que reduz a probabilidade de acumulação (divergência), garantindo uma cobertura uniforme de todo o espaço (“ruído azul”).
Sequências quase aleatórias em uma dimensão
Os métodos para criar sequências quase aleatórias completamente determinadas com baixa divergência em uma dimensão são muito bem estudados e resolvidos em termos gerais. Neste post, considerarei principalmente sequências abertas (infinitas), primeiro em uma dimensão, e depois passarei para dimensões mais altas. A vantagem fundamental de sequências abertas (ou seja, extensível em
n ) reside no fato de que, se o total de erros com base em um número finito de membros for muito grande, a sequência poderá ser expandida sem descartar todos os pontos calculados anteriores. Existem muitas maneiras de criar sequências abertas. Você pode dividir tipos diferentes em categorias pelo método de construir seus parâmetros (hiper) básicos:
- frações irracionais: Kronecker, Richtmayer, Ramshaw
- (mutuamente) números primos: Van der Corpute, Holton, Foret
- Polinômios Irredutíveis: Niederreiter
- Polinômios primitivos: zibelina
Por uma questão de brevidade, neste post vou comparar principalmente o novo aditivo
recursivo R - uma sequência que pertence à primeira categoria, ou seja, a métodos recursivos baseados em números irracionais (geralmente chamados de seqüências de Kronecker,
Weil ou Richtmeier), que são redes de classificação 1, e uma sequência de Holton, que é baseada na sequência canônica van der Corpute unidimensional. A sequência recursiva canônica da Kronecker é definida como:
R_1 (\ alfa): \; \; t_n = \ {s_0 + n \ alpha \}, \ quad n = 1,2,3, ...
onde
alpha - qualquer número irracional. Observe que a entrada
\ {x \} denota a parte fracionária
x . Nos cálculos, essa função é frequentemente expressa como
R1( alpha):tn=s0+n alfa( textrmmod1); quadn=1,2,3,...
At
s0=0 primeiros membros da sequência
R( phi) igual a:
tn=0,618,0,236,0,854,0,472,0,090,0,708,0,327,0,944,0,562,0,180,798,416,0,034,0,652,0,271,0,888,...
É importante notar que o significado
s0 não afeta as características gerais da sequência e, em quase todos os casos, é igual a zero. No entanto, ao calcular a opção
s n e q 0 fornece um grau adicional de liberdade, que geralmente é útil. Se
s n e q 0 , a sequência é freqüentemente chamada de "sequência treliçada deslocada". Apesar do fato de que, por padrão
s = 0 Eu acredito que existem considerações teóricas e práticas para as quais o valor deve ser padrão
s = 1 / 2 . Valor
a l p h a dando a menor discrepância possível se
a l p h a = 1 / p h i onde
p h i - Essa é a proporção áurea. Isso é
p h i e q u i v f r a c s q r t 5 + 1 2 s i m e q 1 , 61803398875 . . . ;
É interessante notar que há um número infinito de outros valores.
a l p h a , o que também nos permite obter a discrepância ideal e todos eles são relacionados um ao outro pela transformação Mobius
alpha′= fracp alpha+qr alpha+s quad textrmparatodososnúmerosinteirosp,q,r,s quad textrmtalque|ps−qr|=1
Agora, comparamos esse método recursivo com as bem conhecidas seqüências de van der Korput com a ordem inversa das descargas [
van der Korput, 1935 ]. As seqüências de Van der Corpute são na verdade uma família de sequências, cada uma das quais é definida por um hiperparâmetro único
b . Os primeiros membros da sequência com b = 2 são iguais:
t[2]n= frac12, frac14, frac34, frac18, frac58, frac38, frac78, frac116, frac916, frac516, frac1316, frac316, frac1116, frac716, frac1516,...
Na próxima seção, comparamos as características gerais e a eficácia de cada uma dessas seqüências. Considere o problema de calcular uma certa integral
A= int10f(x) textrmdx
Podemos aproximar como:
A simeqAn= frac1n sumni=1f(xi), quadxi in[0,1]
- Se \ {x_i \} são iguais i/n , esta é a fórmula dos retângulos ;
- Se \ {x_i \} selecionado aleatoriamente, esse é o método de Monte Carlo ; mas
- Se \ {x_i \} são elementos de uma sequência com baixa divergência, então esse é o método quase-Monte Carlo .
O gráfico abaixo mostra curvas de erro típicas.
sn=|A−An| para aproximar uma certa integral associada a esta função,
f(x)= textrmexp( frac−x22),x in[0,1] para: (i) pontos quase aleatórios da recursão aditiva, quando
alpha=1/ phi , (azul); (ii) pontos quase aleatórios da sequência de van der Corput, (laranja); (iii) pontos selecionados aleatoriamente, (verde); (iv) Sequências de zibelina (vermelho).
Isso mostra que para
n=106 solução de pontos com amostragem aleatória leva a um erro
simeq10−4 , sequência de van der Corput leva a erro
simeq10−6 , considerando que
R( phi) - a sequência leva a um erro
simeq10−7 que em
sim 10 vezes melhor que o erro de van der Corput e
sim 1000 vezes melhor que a amostragem aleatória (uniforme).
Figura 2. Comparação da integração numérica unidimensional usando vários métodos Monte Carlo quase aleatórios. Quanto menor o valor, melhor. Novo R2 - a sequência (azul) e a sequência Sable (vermelho) são obviamente as melhores.Vale a pena mencionar aqui:
- isso corresponde ao conhecimento de que os erros para amostragem aleatória uniforme diminuem assintoticamente para 1/ sqrtn , e o erro para ambas as seqüências quase aleatórias tende a 1/n .
- Resultados para R1( phi) seqüências (azul) e seqüências Sable (vermelho) são as melhores.
- O gráfico demonstra que a sequência de van der Corpute fornece resultados bons, mas incrivelmente consistentes, para tarefas de integração!
- Pode-se ver aqui que para todos os valores n sequência R1( phi) produz melhores resultados do que a sequência de van der Corput.
Nova sequência R1 , que é a sequência Kronecker usando a proporção áurea, é uma das melhores opções para os métodos de integração quase-aleatórios Monte Carlo quase aleatórios (Quasirandom Monte Carlo, QMC).
Também é importante notar que, embora
alpha= phi teoricamente, fornece uma opção comprovadamente ótima,
sqrt2 muito perto do ideal e quase qualquer outro valor irracional
alpha fornece curvas de erro superiores para integração unidimensional. É por isso que é frequentemente usado
alpha= sqrtp para qualquer número primo. Além disso, do ponto de vista dos cálculos, o valor aleatório selecionado no intervalo
alpha em[0,1] quase certamente (dentro dos limites da precisão da máquina) será um número irracional e, portanto, é uma boa escolha para uma sequência com baixa divergência. Para legibilidade visual, a figura acima não mostra os resultados da sequência de Niederreiter, porque eles são praticamente indistinguíveis dos resultados das sequências de Sobol e
R . As seqüências Niederreiter e Sable (juntamente com a seleção otimizada de parâmetros) usadas neste post foram computadas no Mathematica usando o que é chamado de "geradores proprietários fechados e totalmente otimizados da biblioteca Intel MKL" na documentação.
Sequências quase aleatórias em duas dimensões
Os métodos mais modernos para construir uma baixa variação em dimensões mais altas simplesmente combinam (componente por componente)
d sequências unidimensionais. Por uma questão de brevidade, no post consideraremos principalmente a sequência de
Holton [
Holton, 1960 ], a sequência de Sable e
d tridimensional do Kronecker.
A sequência Holton é construída usando simples
d várias sequências van der Corpute unidimensionais, cuja base é mutuamente simples para todas as outras. Ou seja, eles são números coprime em pares. Sem dúvida, a opção mais comum devido à sua óbvia simplicidade e lógica é a escolha do primeiro
d números primos. A distribuição dos primeiros 625 pontos definidos pela sequência (2,3) de Holton é mostrada na Figura 1. Embora muitas seqüências bidimensionais de Holton sejam excelentes fontes de sequências com baixa divergência, é sabido que muitas delas são muito problemáticas e não apresentam baixa divergência. Por exemplo, a Figura 3 mostra que a sequência de Holton (11,13) gera linhas muito perceptíveis. Grandes esforços foram feitos para desenvolver métodos para a seleção de modelos e pares problemáticos.
(p1,p2) . Em dimensões mais altas, o problema se torna ainda mais complicado.
Ao generalizar para dimensões mais altas, os métodos recursivos da Kronecker sofrem dificuldades ainda maiores. Embora usando
alpha= sqrtp Se forem criadas excelentes seqüências unidimensionais, é extremamente difícil encontrar pares de números primos que possam ser usados como base para um caso bidimensional
que não é problemático! Foi sugerido o uso de outros números irracionais conhecidos como solução alternativa, por exemplo
phi, pi,e,... . Eles fornecem resultados moderadamente aceitáveis, mas geralmente não são usados, porque geralmente não são tão bons quanto uma sequência Holton selecionada corretamente. Grandes esforços estão sendo feitos para resolver esses problemas de degeneração.
As soluções propostas usam pular / queimar, pular / afinar. E para codificar (embaralhar) as seqüências finais, outra técnica é usada, freqüentemente usada para superar esse problema. A codificação não pode ser usada para criar uma sequência aberta (infinita) com baixa divergência.
Figura 3. A sequência (11,13) -Holton obviamente não é uma sequência de baixa divergência (esquerda). Também não é a sequência recursiva aditiva (11,13) (no meio). Algumas seqüências recursivas aditivas bidimensionais que usam números irracionais conhecidos são muito boas (à direita).Da mesma forma, apesar dos resultados geralmente melhores da sequência Sable, sua complexidade e, mais importante, a necessidade de uma seleção muito cuidadosa de hiperparâmetros a tornam menos amigável.
Então, novamente, em
d medições:
- seqüências típicas do Kronecker requerem uma escolha d números irracionais linearmente independentes;
- A sequência de Holton requer d prime mutuamente inteiros em pares; mas
- A sequência Sable requer uma escolha d números de guia.
Nova sequência Rd - o único d tridimensional quase aleatória com baixa divergência, não exigindo a escolha de parâmetros básicos.
Generalização da proporção áurea
tl; dr Nesta parte, falarei sobre como construir uma nova classe
d sequencial aberta (infinita) tridimensional com baixa divergência, não exigindo a escolha de parâmetros básicos, com excelentes propriedades de baixa divergência.
Existem muitas maneiras de generalizar a sequência de Fibonacci e / ou a proporção áurea. O método proposto abaixo para generalizar a
proporção áurea não
é novo [
Krchadinac, 2005 ]. Além disso, o polinômio característico está associado a muitas áreas da álgebra, incluindo
números Perron e
números Piso-Vijayaraghavan . No entanto, a conexão explícita entre essa forma generalizada e a construção de seqüências de alta dimensão com baixa divergência é nova nela. Definimos uma visão generalizada da proporção áurea
phid como uma raiz positiva única
xd+1=x+1 . Isto é,
Para
d=1 ,
phi1=1.61803398874989484820458683436563... , que é a proporção de ouro canônica.
Para
d=2 ,
phi2=1.32471795724474602596090885447809... . Esse valor geralmente é chamado de constante de plástico e possui
belas propriedades (veja também
aqui ). Supõe-se que esse valor provavelmente seja ideal para o problema bidimensional correspondente [
Hensley, 2002 ].
Para
d=3 ,
phi3=1.220744084605759475361685349108831...Para
d>3 , embora as raízes desta equação não possuam uma forma algébrica fechada, podemos obter facilmente uma aproximação numérica por métodos padrão, por exemplo, o método de Newton ou observando que, para a seguinte sequência
Rd( phid) :
t0=t1=...=td=1;
tn+d+1=tn+1+tn, quad textrmparan=1,2,3,..
Esta sequência específica de constantes
phid foi nomeado em 1928 pelo arquiteto e monge Hans van de Laan como "
números harmônicos ". Esses significados especiais podem ser expressos de maneira muito elegante da seguinte maneira:
phi1= sqrt1+ sqrt1+ sqrt1+ sqrt1+ sqrt1+...
phi2= sqrt[3]1+ sqrt[3]1+ sqrt[3]1+ sqrt[3]1+ sqrt[3]1+...
phi3= sqrt[4]1+ sqrt[4]1+ sqrt[4]1+ sqrt[4]1+ sqrt[4]1+...
Também temos a seguinte propriedade muito elegante:
phid= limn to infty fractn+1tn
Essa sequência, às vezes chamada de seqüência generalizada ou diferida de Fibonacci, foi estudada profundamente [
As, 2004 ,
Wilson, 1993 ], e a sequência para
d=2 freqüentemente chamada de sequência Padovan [
Stuart, 1996 ,
OEIS A000931 ], e a sequência
d=3 listado em [
OEIS A079398 ]. Como mencionado acima, a principal tarefa deste post é descrever a conexão explícita entre essa sequência generalizada e a construção.
d tridimensionais com baixa divergência.
Resultado principal: os seguintes parâmetros não paramétricos d sequência aberta (infinita) tridimensional Rd( phid) apresenta excelentes características de baixa discrepância em comparação com outros métodos existentes.
\ mathbf {t} _n = \ {n \ pmb {\ alpha} \}, \ quad n = 1,2,3, ...
textrmwhere quad pmb alpha=( frac1 phid, frac1 phi2d, frac1 phi3d,... frac1 phidd)
textrme phid textrméumaraizpositivaúnicaxd+1=x+1
Para duas dimensões, essa sequência generalizada para
n=150 mostrado na figura 1. Os pontos são obviamente distribuídos de maneira muito mais uniforme
R2 sequências -Holton, sequências Kronecker baseadas em
( sqrt3, sqrt7) , Niederreiter e Sable. (Devido à complexidade das seqüências Niederreiter e Sable, elas foram computadas no Mathematica usando um código proprietário fornecido pela Intel.) Esse é o tipo de sequência na qual o vetor base
pmb alpha é uma função de um único valor material, geralmente chamado de sequência de Korobov [Korobov, 1959]
Veja novamente a Figura 1 para comparar várias seqüências bidimensionais e quase aleatórias de baixa divergência.Código e demonstrações
Em uma dimensão, o pseudocódigo para
n membro (
n = 1,2,3, ....) é definido como
g = 1.6180339887498948482 a1 = 1.0/g x[n] = (0.5+a1*n) %1
Em duas dimensões, o pseudocódigo das coordenadas
x e
yn membro (
n = 1,2,3, ....) São definidos como
g = 1.32471795724474602596 a1 = 1.0/g a2 = 1.0/(g*g) x[n] = (0.5+a1*n) %1 y[n] = (0.5+a2*n) %1
Pseudocódigo em três dimensões para coordenadas
x ,
y e
zn membro (
n = 1,2,3, ....) é definido como
g = 1.22074408460575947536 a1 = 1.0/g a2 = 1.0/(g*g) a3 = 1.0/(g*g*g) x[n] = (0.5+a1*n) %1 y[n] = (0.5+a2*n) %1 z[n] = (0.5+a3*n) %1
Modelo de código Python. (observe que as matrizes e loops do Python começam do zero!)
import numpy as np
Escrevi o código de forma que correspondesse à notação matemática usada neste post. No entanto, por razões de convenções de programação e / ou eficiência, algumas modificações merecem destaque. Em primeiro lugar, desde
R2 é uma sequência
recursiva aditiva, formulação alternativa
z que não requer multiplicação de ponto flutuante e mantém alta precisão por muito grande
n tem a forma
z[i+1] = (z[i]+alpha) %1
Em segundo lugar, em linguagens que podem vetorizar, o código de uma função fracionária pode ser vetorizado da seguinte maneira:
for i in range(n): z[i] = seed + alpha*(i+1) z = z %1
Finalmente, podemos substituir essas adições de ponto flutuante e números inteiros multiplicando todas as constantes por
232 e, em seguida, altere a função frac (.) de acordo. Aqui estão as demonstrações do código fonte criadas por outras pessoas com base nesta sequência:
Distância mínima de embalagem
Novo R2 sequência é a única sequência quase - aleatória bidimensional com baixa divergência na qual a distância mínima de empacotamento é reduzida apenas para 1/ sqrtn .
Embora a análise técnica padrão do cálculo da discrepância seja avaliar
d∗ - discrepâncias, primeiro mencionaremos algumas outras formas geométricas (e talvez muito mais intuitivas!) de demonstrar o quanto a nova sequência é preferível a outros métodos padrão. Se denotarmos a distância entre pontos
i e
j para
dij e
d0= textrminfdij o gráfico abaixo mostra como isso varia
d0(n) para
R (2,3) - sequências de Holton, Sable, Niederreiter e sequências aleatórias. Isso pode ser visto na Figura 6.
Como na figura anterior, o valor mínimo da distância é normalizado pelo coeficiente
1/ sqrtn . Você pode perceber que depois
n=300 pontos em uma sequência aleatória (verde) quase certamente dois pontos aparecem extremamente próximos um do outro. Observa-se também que, embora a sequência de Holton (2,3) seja muito melhor que a amostragem aleatória, ela também, infelizmente, diminui assintoticamente para zero. Para a sequência Sable, o motivo da normalização diminui para zero
d0 reside no fato de que o
próprio Sable mostrou que
a sequência
do Sable cai a uma velocidade
/n - o que é bom, mas obviamente muito pior do que
R2 que diminui apenas em
1/ sqrtn .
Para sequência
R( phi2) (azul) a distância mínima entre dois pontos cai constantemente no intervalo entre
0,549/ sqrtn antes
0,868/ sqrtn . Observe que o diâmetro ideal de 0,868 corresponde a um fator de empacotamento de 59,2%. Compare isso com outras
embalagens de círculos .
Observe também que a
amostragem de disco de Bridson Poisson , que
não é expansível para
n e geralmente é recomendado por padrão, ele ainda cria um fator de empacotamento de 49,4%. Vale considerar que o conceito
d0 liga firmemente sequências
phid baixa discrepância com números / vetores pouco aproximados
d medições [
Hensley, 2001 ]. Embora saibamos pouco sobre números pouco aproximados em duas dimensões, a construção
phid pode nos fornecer uma nova visão de números pouco aproximados em dimensões mais altas.
Figura 4. Distância mínima em pares para várias seqüências com baixa divergência. Note que R2 - a sequência (azul) é sempre a melhor opção; Além disso, esta é a única sequência na qual a distância normalizada não tende a zero a n rightarrow infty . A sequência de Holton (laranja) ocupa o segundo lugar, e as seqüências de Sable (verde) e Niederreiter (vermelho) não são tão boas, mas ainda muito melhores que as aleatórias (roxas). Quanto maior, melhor, porque isso corresponde a uma maior distância da embalagem.Diagramas de Voronoi
Outra maneira de visualizar a distribuição uniforme de pontos é criar um diagrama de Voronoi a partir do primeiro
n pontos de uma sequência bidimensional com subsequente coloração de cada área, dependendo de sua
área . A figura abaixo mostra as tabelas de cores Voronoi para (i)
R2 sequências; (ii) (2,3) sequências de Holton; (iii) recursão primária; e (iv) amostragem aleatória simples. Para todas as figuras usadas a mesma escala de cores. Aqui, novamente, é óbvio que
R2 A sequência fornece uma distribuição muito mais uniforme do que a sequência de Holton ou uma amostragem aleatória simples. A imagem é a mesma que acima, colorida apenas de acordo com o número de vértices em cada célula de Voronoi. Não é apenas óbvio aqui que
R - a sequência fornece uma distribuição mais uniforme que Holton ou amostragem aleatória simples, mas o fato de que os valores-chave são mais perceptíveis
n consistem em apenas hexágonos! Se considerarmos a sequência generalizada de Fibonacci, então
A1=A2=A3=1; quadAn+3=An+1+An . Isso é
An :
exibição $$ $$ \ begin {array} {r} 1 & 1 & 1 & 2 & 2 & 3 & 4 & 5 & 7 \\ 9 & \ textbf {12} & 16 & 21 & 28 & 37 & \ textbf {49} & 65 & 86 \\ 114 & \ textbf {151 } & 200 & 265 & 351 & 465 & \ textbf {616} & 816 & 1081 \\ 1432 & \ textbf {1897} & 2513 & 3329 & 4410 & 5842 & \ textbf {7739} & 10252 & 13581 \\ 17991 & \ textbf {23833} & 31572 & 41824 & 55405 {97229} & 128801 & 170625 \\ 226030 & \ textbf {299426} & 396655 & 525456 & 696081 & 922111 & \ textbf {1221537} & 1618192 & 2143648 \\ \ end {array} $$ display $$
Todos os valores em que
n=A9k−2 ou
n=A9k+2 consistem apenas em hexágonos.
Figura 4. Visualização da forma dos diagramas de Voronoi com base na área de cada polígono de Voronoi para (i) R2 sequências; (ii) (2,3) sequências baseadas em números primos; (iii) a sequência (2,3) de Holton; (iv) Niederraiter; (v) zibelina; e (iv) amostragem aleatória simples. As cores indicam o número de lados de cada polígono de Voronoi. Repito: é óbvio que R( phi) A sequência fornece uma distribuição muito mais uniforme do que qualquer outra sequência com uma baixa divergência.Em certos valores n Grade Voronoi para R2 A sequência consiste apenas em hexágonos.
Figura 5. Visualização da forma dos diagramas de Voronoi com base no número de lados de cada polígono de Voronoi para (i) R2 sequências; (ii) (2,3) sequências baseadas em números primos; (iii) a sequência (2,3) de Holton; (iv) Niederraiter; (v) zibelina; e (iv) amostragem aleatória simples. As cores indicam o número de lados de cada polígono de Voronoi. Repito: é óbvio que R( phi) A sequência fornece uma distribuição muito mais uniforme do que qualquer outra sequência com uma baixa divergência.Ladrilhos quase aleatórios de Delaunay para um avião
R sequência é a única sequência quase aleatória de baixa divergência que pode ser usada para criar d inclinações quase-periódicas tridimensionais usando sua malha Delaunay.
A triangulação de Delaunay, que é semelhante ao conde Voronoi, oferece uma oportunidade de analisar essas distribuições de maneira diferente. No entanto, mais importante, a triangulação de Delaunay fornece um novo método para a criação de mosaico quase-periódico (mosaico) de um plano. Triangulação de Delaunay
R2 As sequências fornecem um padrão muito mais uniforme do que uma sequência de Holton ou amostragem aleatória. Em particular, se a triangulação Delaunay de distribuições de pontos for realizada, onde
n igual a qualquer uma das sequências generalizadas de Fibonacci:
AN=$1,1,1,2,3,4,5,7,9,12,16,21,28,37,... , então a triangulação de Delaunay consiste em apenas três triângulos emparelhados de forma idêntica, isto é, em paralelogramos (romboides)! (Exceto para triângulos que têm um vértice comum com um casco convexo.) Além disso,
Em valores n=Ak Triangulação de Delaunay R2 -sequences forma inclinações quasiperiódicas, cada uma das quais consiste em apenas três triângulos básicos (vermelho, amarelo, azul), que estão sempre conectados em pares e formam um mosaico quasiperiódico (mosaico) bem definido do plano com três paralelogramos (romboides).
Figura 6. Visualização da triangulação de Delaunay para (i) R( phi2) sequências; (ii) (2,3) sequências de Holton; (iii) recursão primária; e (iv) amostragem aleatória simples. As cores indicam a área de cada triângulo. Todos os quatro gráficos usam a mesma escala. E aqui novamente, é óbvio que R( phi2) A sequência fornece uma distribuição muito mais uniforme do que qualquer outra sequência com uma baixa divergência.Note que
R2 baseado em
phi2=1.32471795724474602596 sendo o menor número de pisos (um
phi=1,61803... É o maior número de pisos). A conexão de ladrilhos quase-periódicos com números quadráticos e cúbicos de Piso não é nova [
Elkharrat e Masakova], mas acredito que, pela primeira vez, o ladrilho quase-periódico foi criado com base em
phi2=1.324719... .
A animação abaixo demonstra como o Delaunay se malha para a sequência
R2 muda com a adição gradual de pontos. Observe que quando o número de pontos é igual a um membro da sequência generalizada de Fibonacci, toda a grade de Delaunay consiste apenas em paralelogramos vermelhos, azuis e amarelos (romboides), dispostos em uma forma quase-periódica dupla.
Embora o arranjo dos paralelogramos vermelhos demonstre considerável regularidade, pode-se ver claramente que os paralelogramos azul e amarelo são colocados em uma forma quase-periódica. O espectro de Fourier dessa rede pode ser visto na Figura 11, representando os espectros de pontos clássicos. (Observe que uma sequência recursiva baseada em números primos também parece quase periódica no sentido de que é um padrão não repetitivo ordenado. No entanto, seu padrão no intervalo
n não tão constante e também depende criticamente da escolha dos parâmetros básicos. Portanto, focaremos nosso interesse em inclinações quase-periódicas apenas pela sequência
R2 .) Consiste em apenas três triângulos: vermelho, amarelo, azul. Observe que nesta sequência
R( phi2) todos os paralelogramos de cada cor têm o mesmo tamanho e forma. A proporção desses triângulos individuais é incrivelmente elegante. Ou seja
textrmÁrea(vermelha):Área(amarela):Área(azul)=1: phi2: phi22
O mesmo se aplica à frequência relativa de triângulos:
f( textrmvermelho):f( textrmamarelo):f( textrmazul)=1: phi2:1
A partir disso, segue-se que a área relativa total coberta por esses três triângulos no espaço é:
f( textrmvermelho):f( textrmamarelo):f( textrmazul)=1: phi22: phi22
Também pode-se supor que podemos criar esse ladrilho quase-periódico por meio da substituição com base na sequência A. Isso é
A rightarrowB; quadB rightarrowC; quadC rightarrowBA
Para três dimensões, se considerarmos a sequência generalizada de Fibonacci, então
B1=B2=B3=B4=1; quadBn+4=Bn+1+Bn . Isso é
B_n = \ {1,1,1,1,2,2,2,3,4,4,5,7,8,9,12,15,17,21,27,32,38,48,59 , 70,86,107,129, ...
Em certos valores n=Bk Malha 3D Delaunay associada a uma sequência R3 , define uma estrutura de cristal quase-periódica.
Embalagem discreta, parte 2
A figura abaixo mostra o primeiro
n=2500 pontos para cada sequência bidimensional com baixa divergência. Além disso, cada uma das células 50 × 50 = 2500 é colorida em verde somente se contiver
exatamente 1 ponto. Ou seja, quanto mais quadrados verdes, mais uniforme é a distribuição de 2500 pontos em 2500 células. A porcentagem de células verdes para cada uma das figuras é a seguinte:
R2 (75%), Holton (54%), Kronecker (48%), Niederreiter (54%), Sable (49%) e aleatório (38%).
Ondas sonoras
Apenas por diversão, a pedido de
um leitor do News Hacker, modelei como todas essas distribuições de pontos quase aleatórios podem
soar ! Usei a função Listplay do Mathematica: “O
ListPlay [{a1, a2, ...}] cria um objeto que se reproduz como som, cuja amplitude é dada como uma sequência de níveis.” Portanto, sem nenhum comentário, deixarei que você decida por si mesmo quais você gosta mais entre as distribuições quase aleatórias unidimensionais (mono) e distribuições quase aleatórias bidimensionais (estéreo).
| Mono | Stereo |
|---|
| Random | | |
| Sable | | |
| Niederreiter | | |
| Holton | | |
| Kronecker | | |
| R | | |
Conjuntos de baixa discrepância multiclasse
Algumas seqüências de baixa divergência demonstram o que é chamado de "baixa divergência multi-classe". Até esse momento, assumimos que, quando precisamos distribuir o mais uniformemente possível
n pontos, todos os pontos são iguais e indistinguíveis um do outro. No entanto, em muitas situações, existem diferentes tipos de pontos. Consideramos o problema da distribuição uniforme
n para que não apenas todos os pontos sejam distribuídos uniformemente, mas também pontos da mesma classe. Em particular, suponha que haja
nk digitar pontos
k , (onde
n1+n2+n3+...+nk=n ), a distribuição do multiset com uma distribuição baixa é uma distribuição na qual cada
nk pontos distribuídos uniformemente. No nosso caso, descobrimos que
R -A sequência e sequência de Holton é fácil de se adaptar às seqüências de vários conjuntos com baixa divergência, simplesmente colocando pontos alternadamente de cada tipo.
A figura abaixo mostra como eles são distribuídos
n=150 pontos, enquanto 75 são azuis, 40 são apimentados, 25 são verdes e 10 são vermelhos. Para uma sequência recursiva aditiva, isso é resolvido trivialmente: os primeiros 75 membros correspondem simplesmente a azul, os próximos 40 a laranja, os próximos 25 a verde e os últimos 10 a pontos vermelhos. Essa técnica quase funciona para as seqüências de Holton e Kronecker, mas apresenta um desempenho muito ruim nas seqüências de Niederreiter e Sable. Além disso, não existem técnicas conhecidas para a geração contínua de distribuições de pontos em várias escalas nas sequências Niederreiter e Sable. Isso mostra que
distribuições de pontos multiclasses , por exemplo, como os
olhos de galinhas , agora podem ser descritas e construídas diretamente usando sequências com baixa divergência.
Sequência R2 É uma sequência quase aleatória de baixa divergência que fornece fácil construção de uma baixa divergência de várias classes.
Figura 9. Sequências multiescala com baixa divergência. Em sequência R não apenas todos os pontos são distribuídos igualmente, mas também os pontos de cada cor individual.Pontos quase aleatórios em uma esfera
Nos campos da computação gráfica e da física, muitas vezes é necessário distribuir os pontos na superfície de uma esfera tridimensional o mais uniformemente possível. Ao usar seqüências quase aleatórias abertas (infinitas), esse problema é reduzido apenas à colocação de pontos quase aleatórios distribuídos uniformemente em um quadrado unitário na superfície da esfera usando a projeção igual de Lambert. Transformada de projeção padrão de Lambert, colocando um ponto
(u,v) emU[0,1] to(x,y,z) emS2 tem a forma:
(x,y,z)=( cos lambda cos phi, cos lambda sin phi, sin lambda
textrmonde quad cos( lambda− pi/2)=(2u−1); quad phi=2 piv
Uma vez que este
phi2 - a sequência é completamente aberta, permite que você encaixe uma sequência infinita de pontos na superfície da esfera, um ponto de cada vez. Isso contrasta com outros métodos, como a
treliça da espiral de Fibonacci , que exigem o conhecimento prévio do número de pontos. Na inspeção visual, podemos novamente ver claramente que, para
n=1200 novo
R( phi2) - A sequência é muito melhor distribuída do que a sobreposição de Holton ou a amostragem Kronecker, que, por sua vez, é muito mais uniforme que a amostragem aleatória.
Figura 10Pontilhado de computação gráfica
A maioria das técnicas modernas de pontilhamento (por exemplo, pontilhamento de Floyd-Steinberg) são baseadas na distribuição de erros, o que não é muito adequado para processamento paralelo e / ou otimização direta na GPU. Nesses casos, o pontilhamento pontual com máscaras de pontilhamento estático (ou seja, completamente dependente da imagem de destino) mostra excelentes características de desempenho. Provavelmente, as máscaras de pontilhamento mais conhecidas e amplamente usadas são baseadas em matrizes
Bayer , mas as mais novas tentam simular as características do ruído azul mais perto. A dificuldade não trivial de criar máscaras de pontilhamento com base em seqüências de baixa divergência e / ou ruído azul é que essas sequências de baixa divergência projetam um número inteiro
Z para um ponto bidimensional no intervalo
[0,1)2 .
Porém, para uma máscara de pontilhamento, é necessária uma função que projete as coordenadas inteiras bidimensionais da máscara rasterizada em valor de brilho / limite real no intervalo [0,1) .
Sugiro a seguinte abordagem com base em R-sequências. Para cada pixel (x, y) na máscara, atribuímos seu valor de brilhoI(x,y) onde:I(x,y)=α1x+α2y(mod1);
αα=(α1,α2)=(1ϕ2,1ϕ22)
ϕ2 - x3=x+1
Isso é x=1.32471795724474602596… , o que significaα1=0.75487766624669276;α2=0.569840290998
Além disso, se uma função de onda triangular for adicionada para eliminar a descontinuidade causada pela função frac (.) Em cada limite inteiro:T(z)={2z,if 0≤z<1/22−2z,if1/2≤z<1
I(x,y)=T[α1x+α2y(mod1)];
então a máscara e seu diagrama de Fourier / frequência são aprimorados ainda mais. Também observamos que, desdelimn→∞AnAn+1=0.754878;limn→∞AnAn+2=0.56984
então a forma da expressão acima está relacionada à seguinte equação congruenteAnx+An+1y(modAn+2) for integers x,y
Máscaras R pontilhadas criam resultados que competem com métodos modernos baseados em máscaras de ruído azul. Mas, diferentemente das máscaras de ruído azul, elas não precisam ser calculadas com antecedência, porque podem ser calculadas em tempo real.
Vale ressaltar que essa estrutura também foi proposta por Mittring , mas ele encontra os coeficientes empiricamente (e não reproduz os valores finais). Além disso, ajuda a entender por que a fórmula empírica de Jorge Jimenez usada para criar “Call of Duty” (freqüentemente chamada de “Ruído de gradiente intercalado”) funciona tão bem .I(x,y)=(FractionalPart[52.9829189∗FractionalPart[0.06711056∗x+0.00583715∗y]]
No entanto, ele requer 3 multiplicações de ponto flutuante e dois operadores% 1, e a fórmula anterior mostra que podemos fazer isso com apenas duas multiplicações de ponto flutuante e uma operação% 1. Mais importante, porém, este post fornece uma compreensão matemática mais clara do motivo pelo qual uma máscara de pontilhamento nesta forma é tão eficaz, se não ideal. Os resultados dessa matriz de pontilhamento são mostrados abaixo usando a imagem de teste clássica Lena 256 × 256, bem como um padrão de teste de xadrez como exemplo. Ele também mostra os resultados do uso de máscaras de pontilhamento padrão da Bayer, bem como um exemplo com ruído azul. Os dois métodos mais comuns de ruído azul são a amostragem de discos Void-and-Cluster e Poisson. Por uma questão de brevidade, mostrei apenas os resultados do método Void e cluster. [ Peters] O ruído de gradiente intercalado funciona melhor que o Bayer e o ruído azul, mas não tão bom quantoRpontilhamento. Você pode ver que o pontilhamento da Bayer mostra uma notável dissonância do branco nas áreas cinza claro. DitheringR- seqüência e ruído azul são geralmente comparáveis, embora pequenas diferenças possam ser detectadas. Vale a pena notar alguns aspectos do pontilhamento R:- Ele não é isotrópico! Os espectros de Fourier mostram apenas pontos individuais e discretos. Esta é uma característica clássica de inclinações quase-periódicas e espectros de difração de cristais quase-cristais. Em particular, os espectros de Fourier paraR As máscaras correspondem ao fato de que a triangulação de Delaunay para a sequência R canônica consiste em mosaico quase-periódico de três paralelogramos.
- O pontilhamento R quando combinado com uma onda triangular fornece uma máscara incrivelmente uniforme!
- R- , .
- , , R- , .
- (I(x,y) , .
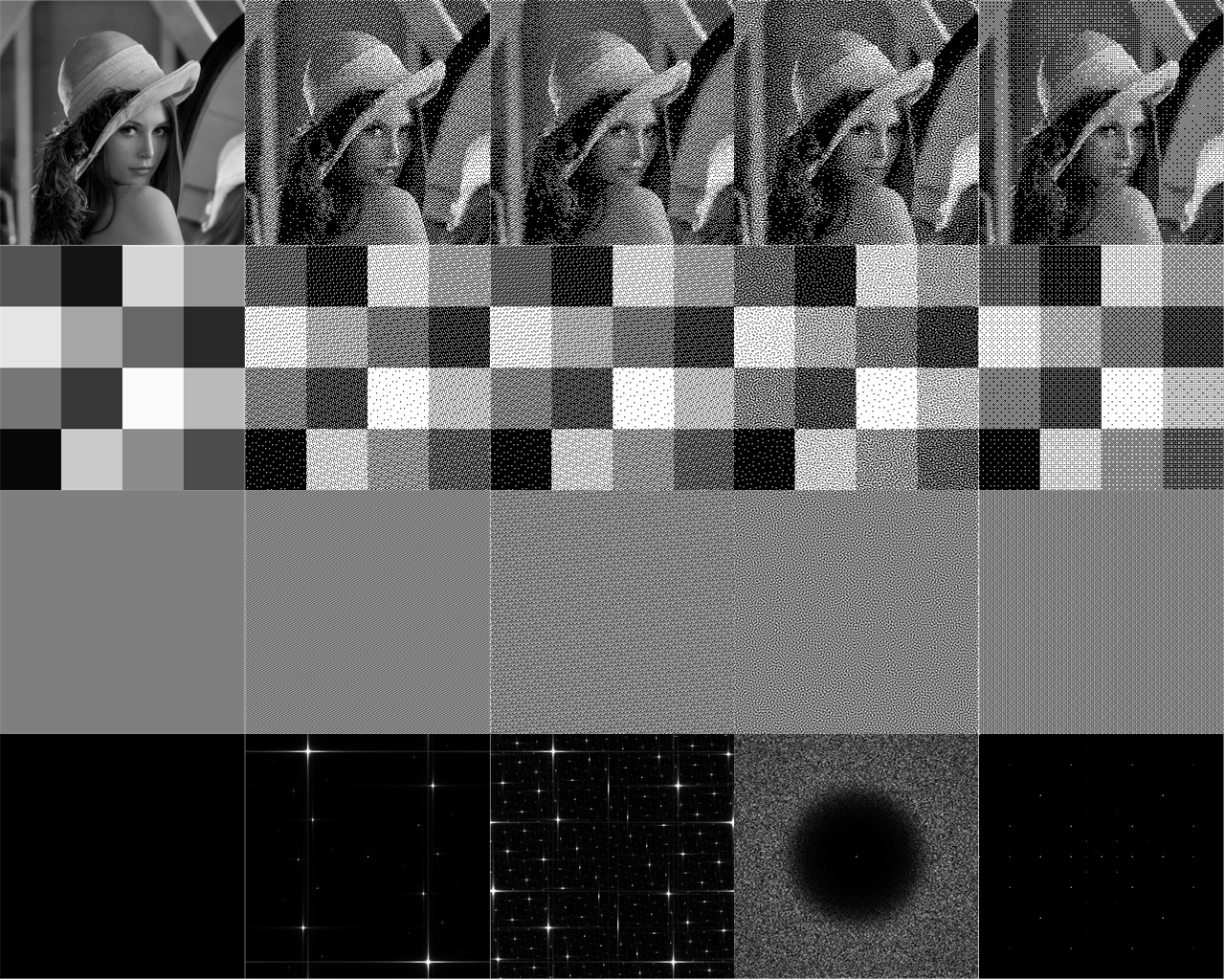
Dimensões mais altas
Semelhante à seção anterior, mas para cinco (5) medições, o gráfico abaixo mostra a distância mínima (global) entre quaisquer dois pontos para R(ϕ5)sequências (2,3,5,7,11) -Holton e sequências aleatórias. Desta vez, o valor normalizado da distância mínima é normalizado por um fator1/5√n .
Você pode ver que, devido à “maldição das dimensões”, a distribuição aleatória é melhor do que todas as seqüências com baixa divergência - com exceção de R5-sequências. EmR(ϕ5) sequências mesmo com n≃106 pontos, a distância mínima entre dois pontos ainda está constantemente próxima 0.8/√n e sempre mais alto 0.631/√n .
Sequência R2 - o único d tridimensional com baixa divergência, na qual a distância da embalagem começa a cair apenas com velocidade n−1/d .
Figura 12. Isso mostra que a sequência R (azul) é consistentemente melhor que Holton (laranja); Zibelina (verde); Niederreiter (vermelho); e aleatório (roxo). Lembre-se de que quanto maior, melhor, porque isso corresponde a uma distância maior da embalagem.Integração numérica
O gráfico a seguir mostra curvas de erro típicas. sn=|A−An| para aproximar uma certa integral associada a uma função gaussiana de meia largura σ=√d ,
f(x)=exp(−x22d),x∈[0,1] , enquanto: (i) Rϕ(azul); (ii) sequência de Holton (laranja); (iii) aleatório (verde); (iv) zibelina (vermelho). O gráfico mostra que, paran=106agora há menos diferenças entre a amostragem aleatória e a sequência de Holton. No entanto, como foi mostrado no caso unidimensional,R- Sequência e Sable são sempre melhores que a sequência de Holton. Também nos permite saber que a sequência de Sable é um pouco melhor.R -sequências.Figura 13. Métodos quase aleatórios de Monte Carlo para integração 8-dimensional. Quanto menor o valor, melhor. A nova sequência R e a sequência Sable mostram-se muito melhores que a sequência Holton.