Chegou outro fim de semana, o que significa que estou escrevendo mais algumas dezenas de linhas de código e fazendo uma ilustração ou duas. Nos artigos anteriores, expliquei como fazer o traçado de raios e até explodir coisas . Isso pode surpreendê-lo, mas a computação gráfica é bastante fácil: mesmo algumas centenas de linhas de C ++ simples podem produzir imagens muito interessantes.

O tópico de hoje é a visão binocular, e nem vamos quebrar a barreira das 100 linhas. Como podemos desenhar cenas em 3D, seria tolice ignorar pares estéreo, então hoje faremos algo assim:




A pura insanidade dos criadores do Magic Carpet ainda me surpreende. Para quem não sabe, este jogo permitiu que você fizesse uma renderização em 3D no modo anaglifo e estereograma no menu principal de configurações ! Isso foi selvagem para mim.

Parallax

Então, vamos começar. Para começar, o que faz com que o nosso aparelho de visão perceba profundidade nos objetos? Existe um termo inteligente "paralaxe". Vamos nos concentrar na tela. Tudo o que está dentro do plano da tela é registrado pelo nosso cérebro como sendo um objeto. Mas se uma mosca voa entre nossos olhos e a tela, o cérebro a percebe como dois objetos. A aranha atrás da tela também será dobrada.



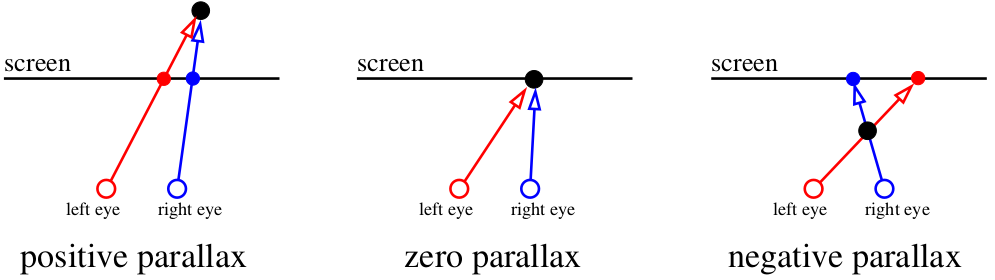
Nosso cérebro é muito eficiente na análise de imagens ligeiramente diferentes. Ele usa disparidade binocular para obter informações sobre a profundidade de imagens 2D provenientes da retina usando estereopsia . Bem, estrague as grandes palavras e vamos desenhar imagens!

Vamos imaginar que nosso monitor é uma janela para o mundo virtual :)



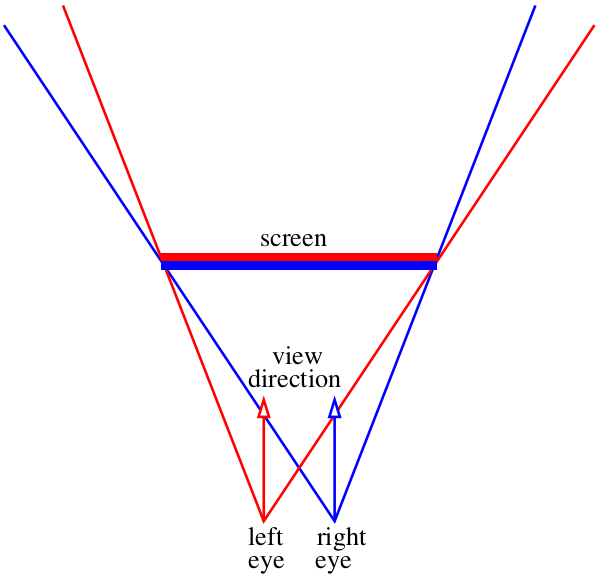
Nossa tarefa é desenhar duas imagens do que vemos através dessa “janela”, uma para cada olho. Na foto acima, o “sanduíche” vermelho-azul. Por enquanto, vamos esquecer como entregar essas imagens ao nosso cérebro. Nesse estágio, precisamos salvar apenas dois arquivos separados. Em particular, quero saber como obter essas imagens usando meu minúsculo traçador de raios .

Vamos assumir que o ângulo não muda e é o vetor (0,0, -1). Vamos supor que podemos mover a câmera para a área entre os olhos, mas e daí? Um pequeno detalhe: a vista da janela através da nossa “janela” é assimétrica. Mas nosso traçador de raios só pode render um frustum simétrico:



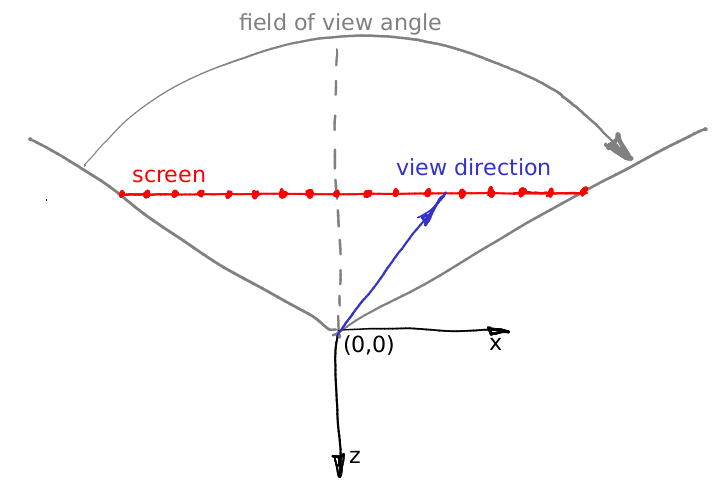
E o que fazemos agora? Cheat :)

Podemos renderizar imagens um pouco mais amplas do que precisamos e depois cortar as partes extras:

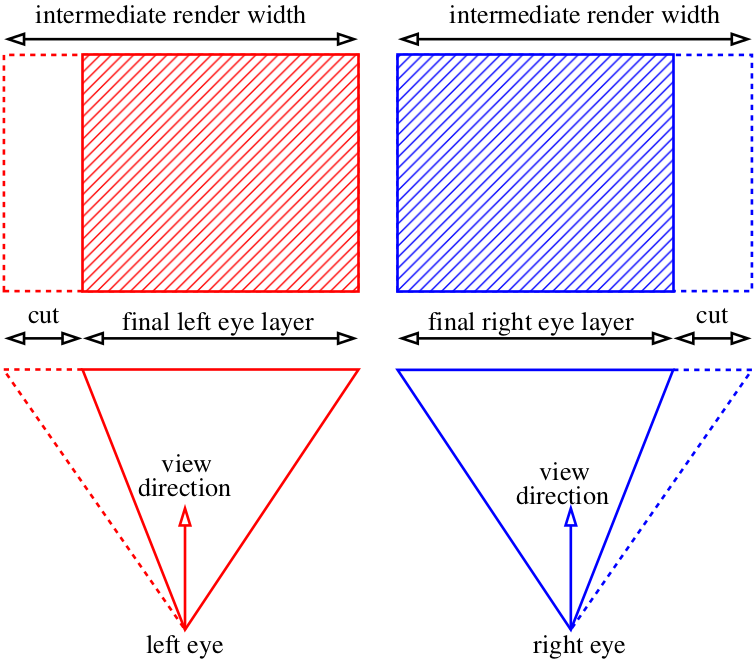
Anaglyph

Acho que cobrimos o mecanismo básico de renderização e agora abordamos a questão de entregar a imagem ao nosso cérebro. A maneira mais simples é esse tipo de óculos:



Fazemos duas renderizações em escala de cinza e atribuímos imagens esquerda e direita aos canais vermelho e azul, respectivamente. Isto é o que obtemos:



O vidro vermelho corta um canal, enquanto o vidro azul corta o outro. Combinados, os olhos têm uma imagem diferente e a percebemos em 3D. Aqui estão as modificações no commit principal do tinyraytracer. As alterações incluem o posicionamento da câmera para montagem de olhos e canais.

O Anaglyph é uma das formas mais antigas de assistir imagens estéreo (geradas por computador). Tem muitas desvantagens, por exemplo, transmissão de cores ruins. Mas, por outro lado, é muito fácil criar em casa.

Se você não possui um compilador no seu computador, não há problema. Se você possui uma conta no guithub, pode visualizar, editar e executar o código (sic!) Em um clique no seu navegador.



Quando você abre esse link, o gitpod cria uma máquina virtual para você, inicia o VS Code e abre um terminal na máquina remota. No histórico de comandos (clique no console e pressione a tecla para cima), existe um conjunto completo de comandos que permite compilar o código, iniciá-lo e abrir a imagem resultante.

Stereoscope

Com os smartphones se tornando populares, lembramos da invenção do século 19 chamada estereoscópio. Há alguns anos, o Google sugeriu o uso de duas lentes (que, infelizmente, são difíceis de criar em casa, você precisa comprá-lo), um pouco de papelão (disponível em qualquer lugar) e um smartphone (no seu bolso) para criar credibilidade Óculos VR.



Eles são abundantes no AliExpress e custam US $ 3 por par. Comparado à renderização de anáglifo, não temos muito o que fazer: basta tirar duas fotos e colocá-las lado a lado. Aqui está o commit .



Estritamente falando, dependendo da lente, talvez seja necessário corrigir a distorção da lente , mas não me incomodei com isso, pois ela parecia bem, independentemente. Mas se realmente precisamos aplicar a pré-distorção do barril que compensa a distorção natural da lente, é assim que fica para o meu smartphone e meus óculos:



Aqui está o link gitpod:

Autostereograms

E o que fazemos se não quisermos usar nenhum equipamento extra? Depois, há apenas uma opção - apertar os olhos. A imagem anterior, honestamente, é suficiente para a visualização estéreo, basta apertar os olhos (cruzando os olhos ou colocando-os na parede). Aqui está um esquema que nos diz como assistir a ilustração anterior. Duas linhas vermelhas mostram as imagens obtidas pela retina esquerda, duas azuis - a retina direita.



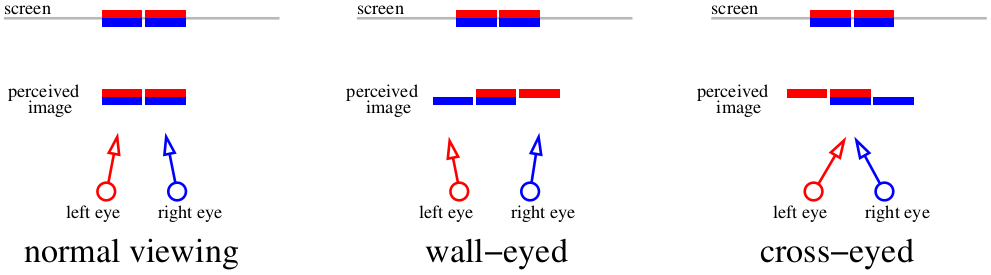
Se focarmos na tela, quatro imagens serão combinadas em duas. Se cruzarmos os olhos ou focarmos em um objeto distante, é possível alimentar "três" imagens do cérebro. As imagens centrais se sobrepõem, o que cria o efeito estéreo.

Pessoas diferentes usam métodos diferentes: por exemplo, não consigo cruzar os olhos, mas os muro facilmente. É importante que o autostereograma criado para um determinado método seja visto apenas com esse método, ou então obtemos um mapa de profundidade invertido (lembra-se de paralaxe positivo e negativo?). O problema é que é difícil cruzar os olhos muito, por isso só funciona em imagens pequenas. Mas e se quisermos os maiores? Vamos sacrificar totalmente as cores e focar apenas na parte da percepção de profundidade. Aqui está a imagem que esperamos obter até o final do artigo:



Este é um autostereograma de olhos nas paredes. Para aqueles que preferem o outro método, aqui está uma imagem para isso . Se você não está acostumado a autostereogramas, tente diferentes condições: tela cheia, imagem menor, brilho, escuridão. Nosso objetivo é cobrir os olhos para que as duas faixas verticais próximas se sobreponham. O mais fácil é focar na parte superior esquerda da imagem, pois é simples. Pessoalmente, abro a imagem em tela cheia. Não se esqueça de remover o cursor do mouse também!

Não pare com um efeito 3D incompleto. Se você vê vagamente formas arredondadas e o efeito 3D é fraco, a ilusão é incompleta. As esferas devem “pular” para fora da tela em direção ao espectador, o efeito deve ser estável e sustentável. A estereopsia tem uma gistese: uma vez que você obtém uma imagem estável, fica mais detalhada quanto mais tempo a observa. Quanto mais os olhos estão da tela, maior o efeito de percepção de profundidade.

Este estereograma foi desenhado usando um método sugerido há 25 anos neste artigo: " Exibindo imagens 3D: algoritmos para estereogramas de pontos aleatórios de imagem única ".

Vamos começar

O ponto de partida para renderizar autostereogramas é o mapa de profundidade (já que abandonamos as cores). Esta confirmação desenha a seguinte imagem:



Os planos mais próximos e futuros definem nossa profundidade: o ponto mais distante do meu mapa tem a profundidade de 0, enquanto o ponto mais próximo tem a profundidade de 1.

Os princípios fundamentais

Digamos que nossos olhos estejam a uma distância d da tela. Colocamos nosso plano distante (imaginário) (z = 0) na mesma distância "atrás" da tela. Escolhemos a variável µ, que determina a localização do plano próximo (z = 1), que estará à distância µd do plano distante. Para o meu código, escolhi μ = ⅓. No geral, todo o nosso "mundo" vive à distância de d-μd em d atrás da tela. Digamos que sabemos a distância entre os olhos (em pixels, eu escolhi 400 pixels):



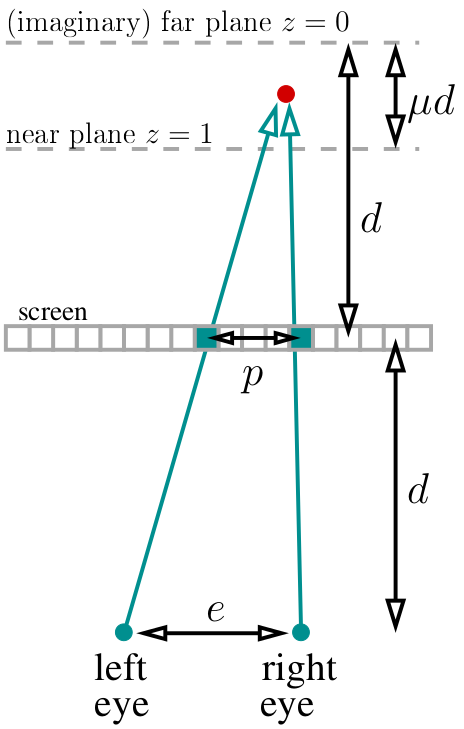
Se observarmos o ponto vermelho, dois pixels marcados em verde devem ter a mesma cor no estereograma. Como calcular a distância entre eles? Fácil Se o ponto projetado atual tiver a profundidade de z, a paralaxe dividida pela distância entre os olhos será igual à fração entre as profundidades correspondentes: p / e = (d-dμz) / (2d-dμz). A propósito, observe que d é simplificado e não aparece em nenhum outro lugar! Então p / e = (1-μz) / (2-μz), significando que a paralaxe é igual a p = e * (1-μz) / (2-μz) pixels.

A principal idéia por trás do autostereograma é: percorremos todo o mapa de profundidade, para cada valor de profundidade, determinamos quais pixels terão a mesma cor e o colocamos em nosso sistema de restrições. Começamos a partir da imagem aleatória e tentamos satisfazer todas as restrições que definimos anteriormente.

Preparando a imagem de origem

Aqui preparamos a imagem que mais tarde será restringida por restrições de paralaxe. Aqui está o commit , e ele desenha o seguinte:



Observe que as cores são na maioria aleatórias, além do canal vermelho onde eu coloquei rand () * sin para criar um padrão periódico. As faixas estão separadas por 200 pixels, que é (dado μ = 1/3 e e = 400) o valor máximo de paralaxe em nosso mundo (o plano distante). O padrão não é tecnicamente necessário, mas ajudará a focar os olhos.

Renderização automática

Na verdade, o código completo que desenha o autostereograma se parece com isso:

int parallax(const float z) { const float eye_separation = 400.; // interpupillary distance in pixels const float mu = .33; // if the far plane is a distance D behind the screen, then the near plane is a distance mu*D in front of the far plane return static_cast<int>(eye_separation*((1.-z*mu)/(2.-z*mu))+.5); } size_t uf_find(std::vector<size_t> &same, size_t x) { return same[x]==x ? x : uf_find(same, same[x]); } void uf_union(std::vector<size_t> &same, size_t x, size_t y) { if ((x=uf_find(same, x)) != (y=uf_find(same, y))) same[x] = y; } int main() { [...] for (size_t j=0; j<height; j++) { // autostereogram rendering loop std::vector<size_t> same(width); std::iota(same.begin(), same.end(), 0); // initialize the union-find data structure (same[i]=i) for (size_t i=0; i<width; i++) { // put the constraints int par = parallax(zbuffer[i+j*width]); int left = i - par/2; int right = left + par; // works better than i+par/2 for odd values of par if (left>=0 && right<(int)width) uf_union(same, left, right); // left and right pixels will have the same color } for (size_t i=0; i<width; i++) { // resolve the constraints size_t root = uf_find(same, i); for (size_t c=0; c<3; c++) framebuffer[(i+j*width)*3+c] = framebuffer[(root+j*width)*3+c]; } } [...] 

Aqui está o commit , a função int paralaxe (const float z) nos fornece distância entre pixels da mesma cor para o valor atual da profundidade. Renderizamos o estereograma linha por linha, uma vez que as linhas são independentes uma da outra (não temos paralaxe vertical). O loop principal simplesmente itera através de cada linha; cada vez que começa com um conjunto ilimitado de pixels e, para cada pixel, adiciona uma restrição de igualdade. No final, ele nos fornece um certo número de agrupamentos de pixels da mesma cor. Por exemplo, pixels com índices esquerdo e direito devem acabar idênticos.

Como armazenar esse conjunto de restrições? A maneira mais simples é a estrutura de dados de localização de união . Não vou entrar em detalhes, basta ir à Wikipedia, são literalmente três linhas de código. O ponto principal é que, para cada cluster, existe um determinado pixel "raiz" responsável pelo cluster. O pixel raiz mantém sua cor inicial e todos os outros pixels do cluster devem ser atualizados:

  for (size_t i=0; i<width; i++) { // resolve the constraints size_t root = uf_find(same, i); for (size_t c=0; c<3; c++) framebuffer[(i+j*width)*3+c] = framebuffer[(root+j*width)*3+c]; } 

Conclusão

É isso mesmo. Vinte linhas de código e nosso autostereograma está pronto para você quebrar os olhos. A propósito, se nos esforçarmos o suficiente, é possível transmitir informações sobre cores.

Não cobri outros sistemas estereoscópicos, como os sistemas 3D polarizados , pois são muito mais caros de fabricar. Se eu perdi alguma coisa, fique à vontade para me corrigir!