Programação relacional: dor, interesse e dor novamente

No post anterior, falamos detalhadamente o que ensinamos aos alunos no campo da "Programação Industrial". Para aqueles cuja área de interesse se encontra em um campo mais teórico, por exemplo, atraído por novos paradigmas de programação ou matemática abstrata usada na pesquisa teórica sobre programação, existe outra especialização - “Linguagens de Programação”.

Hoje vou falar sobre minha pesquisa no campo da programação relacional, que faço na universidade e como pesquisadora-estudante no laboratório de ferramentas de linguagem JetBrains Research.

O que é programação relacional? Normalmente, executamos uma função com argumentos e obtemos o resultado. E, no caso relacional, você pode fazer o oposto: fixar o resultado e um argumento e obter o segundo argumento. O principal é escrever o código corretamente, ser paciente e ter um bom cluster.

Sobre mim

Meu nome é Dmitry Rozplokhas, sou aluno do primeiro ano do HSE de São Petersburgo e, no ano passado, me formei no programa de bacharelado da Universidade Acadêmica na área de "Linguagens de Programação". Desde o terceiro ano de graduação, também sou estudante de pesquisa no laboratório de ferramentas de linguagem JetBrains Research.

Programação relacional

Fatos gerais

A programação relacional é quando, em vez de funções, você descreve a relação entre argumentos e o resultado. Se o idioma for aprimorado para isso, você poderá obter alguns bônus, por exemplo, a capacidade de executar a função na direção oposta (restaurar os possíveis valores dos argumentos como resultado).

Em geral, isso pode ser feito em qualquer linguagem lógica, mas o interesse pela programação relacional surgiu simultaneamente com o advento de uma miniKanren de linguagem lógica pura minimalista há cerca de dez anos, o que tornou possível descrever e usar convenientemente essas relações.

Aqui estão alguns dos casos de uso mais avançados: você pode escrever um verificador de provas e usá-lo para encontrar evidências ( Near et al., 2008 ) ou criar um intérprete para algum idioma e usá-lo para gerar programas de suíte de testes ( Byrd et al., 2017 ).

Exemplo de sintaxe e brinquedo

O miniKanren é uma linguagem pequena; apenas construções matemáticas básicas são usadas para descrever relações. Essa é uma linguagem incorporada, suas primitivas são uma biblioteca para alguma linguagem externa e pequenos programas miniKanren podem ser usados ​​dentro de um programa em outro idioma.

Idiomas estrangeiros adequados para miniKanren, um monte. Inicialmente, havia o Scheme, estamos trabalhando com a versão para Ocaml ( OCanren ), e a lista completa pode ser vista em minikanren.org . Os exemplos deste artigo também estarão no OCanren. Muitas implementações adicionam funções auxiliares, mas focaremos apenas no idioma principal.

Vamos começar com os tipos de dados. Convencionalmente, eles podem ser divididos em dois tipos:

• Constantes são alguns dados do idioma em que estamos inseridos. Strings, números e até matrizes. Mas para o miniKanren básico, tudo isso é uma caixa preta, as constantes só podem ser verificadas quanto à igualdade.
  
• Um "termo" é uma tupla de vários elementos. Geralmente usado da mesma maneira que os construtores de dados no Haskell: construtor de dados (string) mais zero ou mais parâmetros. OCanren usa construtores de dados regulares do OCaml.
  

Por exemplo, se queremos trabalhar com matrizes no próprio miniKanren, ele deve ser descrito em termos de termos semelhantes às linguagens funcionais - como uma lista conectada individualmente. Uma lista é uma lista vazia (indicada por algum termo simples) ou um par do primeiro elemento da lista ("cabeçalho") e dos elementos restantes ("rabo").

let emptyList = Nil let list_123 = Cons (1, Cons (2, Cons (3, Nil))) 

Um programa miniKanren é o relacionamento entre algumas variáveis. Na inicialização, o programa fornece todos os valores possíveis das variáveis ​​de forma geral. Muitas vezes, as implementações permitem limitar o número de respostas na saída, por exemplo, encontrar apenas a primeira - a pesquisa nem sempre pára depois de encontrar todas as soluções.

Você pode escrever vários relacionamentos que são definidos um pelo outro e até chamados recursivamente como funções. Por exemplo, abaixo, em vez da função $$$append (a, b) → com$definir a relação $$$appendo (a, b, c)$: lista $$$c$é uma concatenação de listas $$$a$e $$$b$. As funções que retornam relacionamentos tradicionalmente terminam com um "o" para distingui-las das funções comuns.

Uma relação é escrita como uma declaração sobre seus argumentos. Temos quatro operações básicas :

• Unificação ou igualdade (===) de dois termos, os termos podem incluir variáveis. Por exemplo, você pode escrever a relação "list $$$l$consiste em um elemento $$$x$":
  
  

   let isSingletono xl = l === Cons (x, Nil) 

• Conjunção (lógica “e”) e disjunção (lógica “ou”) - como na lógica comum. OCanren é referido como &&& e |||. Mas basicamente não há negação lógica no MiniKanren.
  
• Adicionando novas variáveis. Na lógica, é um quantificador da existência. Por exemplo, para verificar a lista sem vazios, é necessário verificar se a lista consiste em uma cabeça e uma cauda. Eles não são argumentos do relacionamento, então você precisa criar novas variáveis:
  
  

   let nonEmptyo l = fresh (ht) (l === Cons (h, t)) 

Um relacionamento pode se chamar recursivamente. Por exemplo, você precisa definir o elemento "relacionamento" $$$x$está na lista ". Resolveremos esse problema analisando casos triviais, como em linguagens funcionais:

1. Ou o chefe da lista é $$$x$
   
2. Ou $$$x$encontra-se na cauda
   

 let membero lx = fresh (ht) ( (l === Cons (h, t)) &&& (x === h ||| membero tx) ) 

A versão básica do idioma é construída nessas quatro operações. Existem também extensões que permitem usar outras operações. O mais útil deles é a restrição de desigualdade para definir a desigualdade de dois termos (= / =).

Apesar do minimalismo, o miniKanren é uma linguagem bastante expressiva. Por exemplo, observe a concatenação relacional de duas listas. A função de dois argumentos se transforma em uma relação tripla " $$$ab$é uma concatenação de listas $$$a$e $$$b$"

 let appendo ab ab = (a === Nil &&& ab === b) ||| (fresh (ht tb) (*  :  fresh   &&& *) (a = Cons (h, t)) (appendo tb tb) (ab === Cons (h, tb))) 

A solução não é estruturalmente diferente de como a escreveríamos em uma linguagem funcional. Analisamos dois casos unidos por uma cláusula:

1. Se a primeira lista estiver vazia, a segunda lista e o resultado da concatenação serão iguais.
   
2. Se a primeira lista não estiver vazia, analisamos-a na cabeça e no final e construímos o resultado usando uma chamada recursiva da relação.
   

Podemos fazer uma solicitação para essa relação, corrigindo o primeiro e o segundo argumento - obtemos a concatenação de listas:

 run 1 (λ q -> appendo (Cons (1, Cons (2, Nil))) (Cons (3, Cons (4, Nil))) q) 

⇒

 q = Cons (1, Cons (2, Cons (3, Cons (4, Nil)))) 

Podemos consertar o último argumento - dividimos todas as partições desta lista em duas.

 run 4 (λ qr -> appendo qr (Cons (1, Cons (2, Cons (3, Nil))))) 

⇒

 q = Nil, r = Cons (1, Cons (2, Cons (3, Nil))) | q = Cons (1, Nil), r = Cons (2, Cons (3, Nil)) | q = Cons (1, Cons (2, Nil)), r = Cons (3, Nil) | q = Cons (1, Cons (2, Cons (3, Nil))), r = Nil 

Você pode fazer qualquer outra coisa. Um exemplo um pouco mais fora do padrão, no qual corrigimos apenas parte dos argumentos:

 run 1 (λ qr -> appendo (Cons (1, Cons (q, Nil))) r (Cons (1, Cons (2, Cons (3, Cons (4, Nil)))))) 

⇒

 q = 2, r = Cons (3, Cons (4, Nil)) 

Como isso funciona

Do ponto de vista da teoria, não há nada impressionante aqui: você sempre pode começar a procurar todas as opções possíveis para todos os argumentos, verificando para cada conjunto se eles se comportam em relação a uma determinada função / relacionamento como gostaríamos (consulte "O Museu Britânico do Algoritmo" ) . De interesse é o fato de que aqui a busca (em outras palavras, a busca por uma solução) utiliza apenas a estrutura do relacionamento descrito, devido ao qual pode ser relativamente eficaz na prática.

A pesquisa está relacionada à acumulação de informações sobre várias variáveis ​​no estado atual. Não sabemos nada sobre cada variável ou sabemos como ela é expressa em termos, valores e outras variáveis. Por exemplo:

b = Cons (x, y)
c = Cons (10, z)
x = ?
y = ?
z = ?

Ao passar pela unificação, analisamos dois termos com essas informações em mente e atualizamos o estado ou encerramos a pesquisa se dois termos não puderem ser unificados. Por exemplo, ao concluir a unificação b = c, obtemos novas informações: x = 10, y = z. Mas a unificação b = Nil causará uma contradição.

Procuramos em conjunto sequencialmente (para que a informação se acumule) e, em uma disjunção, dividimos a busca em dois ramos paralelos e seguimos em frente, alternando passos neles - essa é a chamada busca intercalada. Graças a essa alternância, a pesquisa está concluída - todas as soluções adequadas serão encontradas após um tempo finito. Por exemplo, na linguagem Prolog, isso não é verdade. Ele faz algo como um rastreamento profundo (que pode ficar pendurado em um galho infinito), e a intercalação de pesquisas é essencialmente uma modificação complicada de rastreamento amplo.

Vamos agora ver como a primeira consulta da seção anterior funciona. Como o appendo possui chamadas recursivas, adicionaremos índices às variáveis ​​para distingui-las. A figura abaixo mostra a árvore de enumeração. As setas indicam a direção da disseminação da informação (com exceção do retorno da recursão). Entre disjunções, as informações não são distribuídas e entre conjunções, da esquerda para a direita.

1. Começamos com uma chamada externa para appendo. Ramo esquerdo da disjunção morre devido a controvérsia: lista $$$a$não está vazio.
   
2. No ramo direito, são introduzidas variáveis ​​auxiliares, que são usadas para "analisar" a lista $$$a_1$na cabeça e cauda.
   
3. Depois disso, a chamada recorrente recursiva ocorre para a = [2], b = [3, 4], ab = ?, Na qual operações semelhantes ocorrem.
   
4. Mas na terceira chamada para apêndice já temos a = [], b = [3,4], ab =?, E então a disjunção esquerda simplesmente funciona, após o que obtemos as informações ab = b. Mas no ramo certo há uma contradição.
   
5. Agora podemos escrever todas as informações disponíveis e restaurar a resposta substituindo os valores das variáveis:
   
   a_1 = [1, 2]
b_1 = [3, 4]
ab_1 = Cons h_1 tb_1
h_1 = 1
a_2 = t_1 = [2]
b_2 = b_1 = [3, 4]
ab_2 = tb_1 = Cons h_2 tb_2
h_2 = 2
a_3 = t_2 = Nil
b_3 = b_2 = b_1 = [3, 4]
ab_3 = tb_2 = b_3 = [3, 4]

   
6. Segue-se que $$$ab_1$= Contras (1, Contras (2, [3, 4])) = [1, 2, 3, 4], conforme necessário.
   

O que eu fiz na graduação

Tudo fica mais lento

Como sempre: eles prometem que tudo será super declarativo, mas, na realidade, você precisa se adaptar à linguagem e escrever tudo de uma maneira especial (tendo em mente como tudo será executado) para que pelo menos algo funcione, exceto os exemplos mais simples. Isso é decepcionante.

Um dos primeiros problemas que um programador iniciante em miniKanren enfrenta é que depende muito da ordem em que você descreve as condições (conjuntos) no programa. Com um pedido, está tudo bem, mas duas conjunções foram trocadas e tudo começou a funcionar muito devagar ou nem terminou. Isso é inesperado.

Mesmo no exemplo com appendo, iniciar na direção oposta (gerando dividir a lista em duas) não termina, a menos que você especifique explicitamente quantas respostas deseja (a pesquisa será encerrada depois que o número necessário for encontrado).

Suponha que consertemos as variáveis ​​originais da seguinte maneira: a = ?, B = ?, Ab = [1, 2, 3] (veja a figura abaixo) No segundo ramo, essas informações não serão usadas de forma alguma durante a chamada recursiva (a variável ab e restrições de $$$h_1$e $$$tb_1$aparecer somente após esta chamada). Portanto, na primeira chamada recursiva, todos os seus argumentos serão variáveis ​​livres. Essa chamada gerará todos os tipos de triplos a partir de duas listas e de suas concatenações (e essa geração nunca terminará) e, dentre elas, serão escolhidas aquelas para as quais o terceiro elemento resultou exatamente da maneira que precisamos.



Tudo não é tão ruim quanto parece à primeira vista, porque vamos resolver esses triplos em grandes grupos. Listas com o mesmo comprimento, mas elementos diferentes não diferem do ponto de vista da função, portanto elas se enquadram em uma solução - haverá variáveis ​​livres no lugar dos elementos. No entanto, ainda estaremos classificando todos os comprimentos de lista possíveis, embora precisemos apenas de um e sabemos qual. Este é um uso muito irracional (não-uso) de informações na pesquisa.

Este exemplo específico é fácil de corrigir: você só precisa mover a chamada recursiva para o final e tudo funcionará como deveria. Antes da chamada recursiva, a unificação com a variável ab ocorrerá e a chamada recursiva será feita a partir da cauda da lista fornecida (como uma função recursiva normal). Essa definição com uma chamada recursiva no final funcionará bem em todas as direções: para a chamada recursiva, conseguimos acumular todas as informações possíveis sobre os argumentos.

No entanto, em qualquer exemplo um pouco mais complexo, quando existem várias chamadas significativas, não existe uma ordem específica para a qual tudo ficará bem. O exemplo mais simples: expandindo uma lista usando concatenação. Consertamos o primeiro argumento - precisamos dessa ordem específica, consertamos o segundo - precisamos trocar as chamadas. Caso contrário, é pesquisado por um longo tempo e a pesquisa não termina.

 reverso x xr = (x === Nil &&& xr == Nil) ||| (fresh (ht tr) (x === Cons (h, t)) (reverso t tr) (appendo tr (Cons (h, Nil)) xr)) 

Isso ocorre porque intercalar os processos de pesquisa em conjunto sequencialmente, e ninguém poderia pensar em como fazê-lo de maneira diferente sem perder a eficiência aceitável, apesar de tentarem. É claro que um dia todas as soluções serão encontradas, mas com a ordem errada, elas serão pesquisadas por um tempo tão irrealista que não há sentido prático nisso.

Existem técnicas para escrever programas para evitar esse problema. Mas muitos deles exigem habilidade e imaginação especiais para serem usados, e o resultado são programas muito grandes. Um exemplo é o termo técnica de delimitação de tamanho e a definição de divisão binária com o restante através da multiplicação com sua ajuda. Em vez de escrever estupidamente uma definição matemática

 divo nmqr = (fresh (mq) (multo mq mq) (pluso mq rn) (lto rm)) 

Eu tenho que escrever uma definição recursiva de 20 linhas + uma grande função auxiliar que não é realista de ler (eu ainda não entendo o que está sendo feito lá). Pode ser encontrada na dissertação de Will Bird na seção Aritmética Binária Pura.

Em vista do exposto, gostaria de apresentar algum tipo de modificação de pesquisa para que programas simples e escritos naturalmente também funcionem.

Otimizar

Percebemos que quando tudo está ruim, a pesquisa não termina, a menos que você indique explicitamente o número de respostas e o quebre. Portanto, eles decidiram lutar precisamente com a incompletude da pesquisa - é muito mais fácil concretizar do que "funciona por muito tempo". Em geral, é claro, eu só quero acelerar a pesquisa, mas é muito mais difícil formalizar, então começamos com uma tarefa menos ambiciosa.

Na maioria dos casos, quando a pesquisa diverge, ocorre uma situação fácil de rastrear. Se uma função é chamada recursivamente e em uma chamada recursiva, os argumentos são os mesmos ou menos específicos; na chamada recursiva, outra subtarefa é gerada novamente e ocorre uma recursão infinita. Formalmente, soa assim: há uma substituição, aplicando qual aos novos argumentos, obtemos os antigos. Por exemplo, na figura abaixo, uma chamada recursiva é uma generalização do original: você pode substituir $$$c_2$= [x, 3], $$$d_2$= x e receba a ligação original.



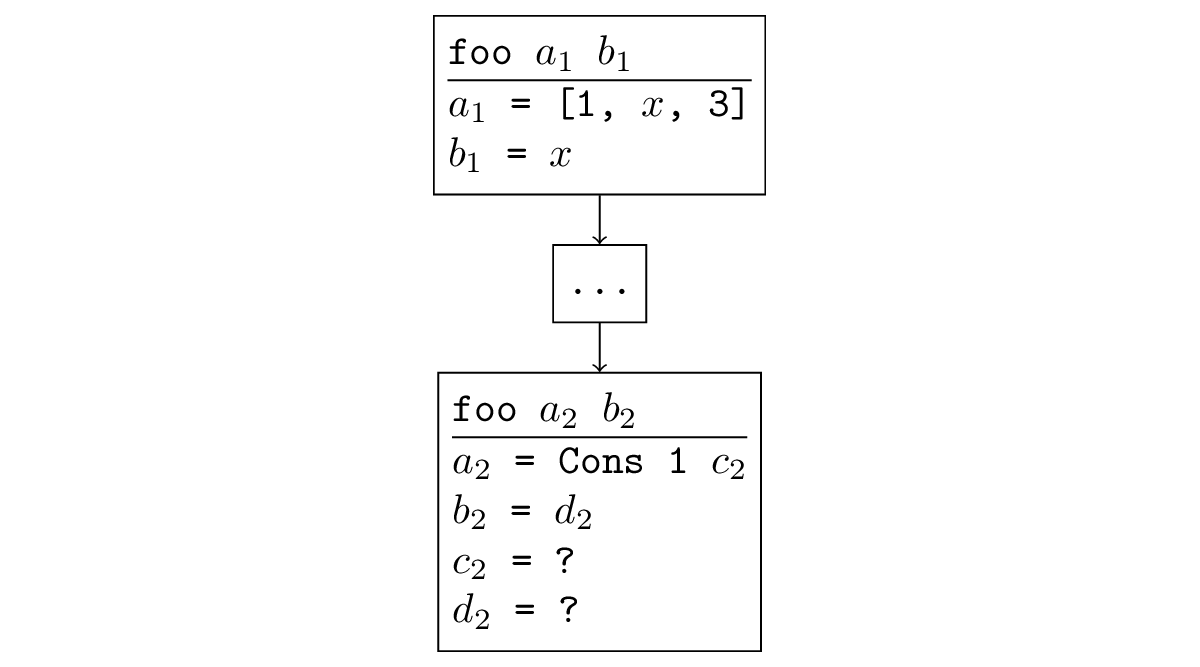
Pode-se traçar que essa situação também ocorre nos exemplos de divergência que já conhecemos. Como escrevi anteriormente, quando você executa o appendo na direção oposta, uma chamada recursiva será feita com variáveis ​​livres em vez de todas as variáveis, o que, é claro, é menos específico que a chamada original, na qual o terceiro argumento foi corrigido.

Se executarmos reverso com x =? e xr = [1, 2, 3], pode-se ver que a primeira chamada recursiva ocorrerá novamente com duas variáveis ​​livres, de modo que novos argumentos poderão ser obviamente transferidos novamente para os anteriores.

 reverso x x_r  (* x = ?, x_r = [1, 2, 3] *) fresh (ht t_r) (x === Cons (h, t)) (* x_r = [1, 2, 3] = Cons 1 (Cons 2 (Cons 3 Nil))) x = Cons (h, t) *) (reverso t t_r) (* :   t=x, t_r=[1,2,3],    *) 

Usando esse critério, podemos detectar divergências no processo de execução do programa, entender que tudo está ruim com essa ordem e alterá-la dinamicamente para outra. Graças a isso, idealmente, a ordem certa será selecionada para cada chamada.
Você pode fazer isso de forma ingênua: se for encontrada divergência no conjunto, martelamos todas as respostas que ele já encontrou e adiamos sua execução para mais tarde, “pulando para a frente” no próximo conjunto. Então, talvez, quando continuarmos a executá-lo, mais informações já serão conhecidas e divergências não surgirão. Em nossos exemplos, isso levará aos conjuntos de trocas desejados.

Existem maneiras menos ingênuas que permitem, por exemplo, não perder o trabalho já realizado, adiando o desempenho. Já com a variante mais estúpida de mudar a ordem, a divergência desapareceu em todos os exemplos simples que sofrem com a não comutatividade da conjunção que conhecemos, incluindo

• ordenar a lista de números (é também a geração de todas as permutações da lista),
  
• Aritmética peano e aritmética binária,
  
• geração de árvores binárias de um determinado tamanho.
  

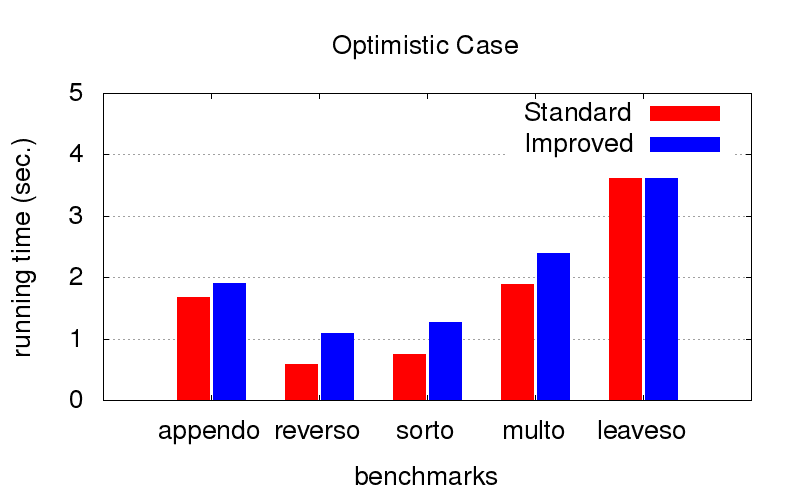
Foi uma surpresa inesperada para nós. Além da divergência, a otimização também combate a desaceleração do programa. Os diagramas abaixo mostram o tempo de execução de programas com duas ordens diferentes em conjunções (relativamente falando, uma das melhores e uma das muitas ruins). Foi lançado em um computador com a configuração da CPU Intel Core i7 M 620, 2,67 GHz x 4, 8 GB de RAM com o sistema operacional Ubuntu 16.04.

Quando a ordem já é ótima (nós a selecionamos manualmente), a otimização diminui um pouco a execução, mas não é crítica


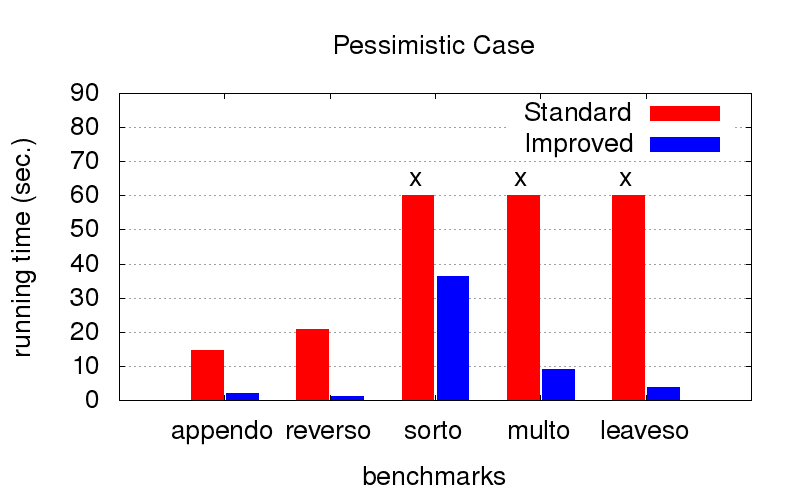
Mas quando o pedido não é o ideal (por exemplo, adequado apenas para o lançamento na direção oposta), com a otimização, o resultado é muito mais rápido. As cruzes significam que mal podíamos esperar pelo fim, funciona muito mais tempo

Como quebrar nada

Tudo isso foi baseado puramente na intuição e queríamos provar isso estritamente. Teoria, afinal.

Para provar algo, precisamos de semântica formal da linguagem. Descrevemos a semântica operacional para o miniKanren. Esta é uma versão simplificada e matematizada de uma implementação de linguagem real. Ele usa uma versão muito limitada (portanto fácil de usar), na qual você pode especificar apenas a execução final dos programas (a pesquisa deve ser final). Mas, para nossos propósitos, é exatamente isso que é necessário.

Para provar o critério, o lema é formulado primeiro: a execução do programa a partir de um estado mais geral funcionará mais. Formalmente: a árvore de saída na semântica tem uma grande altura. Isso é provado por indução, mas a afirmação deve ser generalizada com muito cuidado, caso contrário, a hipótese indutiva não será suficientemente forte. Segue-se desse lema que, se um critério funcionou durante a execução do programa, a árvore de saída possui sua própria subárvore de altura maior ou igual. Isso contradiz, pois para a semântica indutivamente dada, todas as árvores são finitas. Isso significa que, em nossa semântica, a execução deste programa é inexprimível, o que implica que a pesquisa nele não termina.

O método proposto é conservador: só mudamos algo quando estamos convencidos de que tudo já está completamente ruim e impossível de piorar; portanto, não quebramos nada em termos de conclusão do programa.

A prova principal contém muitos detalhes; portanto, tínhamos o desejo de verificá-la formalmente escrevendo para a Coq . No entanto, tecnicamente, era bastante difícil, então acalmamos nosso ardor e nos envolvemos seriamente na verificação automática apenas na magistratura.

Postagem

No meio do trabalho, apresentamos este estudo na sessão de pôsteres do ICFP-2017 no Student Research Competition . Lá nos encontramos com os criadores da linguagem - Will Bird e Daniel Friedman - e eles disseram que isso é significativo e precisamos analisá-la com mais detalhes. A propósito, Will geralmente é amigo de nosso laboratório na JetBrains Research. Toda a nossa pesquisa sobre o miniKanren começou quando, em 2015, Will realizou uma escola de verão em programação relacional em São Petersburgo.

Um ano depois, levamos nosso trabalho a um formulário mais ou menos completo e apresentamos o artigo nos Princípios e Práticas da Programação Declarativa 2018.

O que eu faço na pós-graduação

Queríamos continuar engajados na semântica formal do miniKanren e na prova rigorosa de todas as suas propriedades. Na literatura, geralmente propriedades (geralmente longe de óbvias) são simplesmente postuladas e demonstradas usando exemplos, mas ninguém prova nada. Por exemplo, o livro principal sobre programação relacional é uma lista de perguntas e respostas, cada uma dedicada a um pedaço de código específico. Mesmo para a declaração de integridade da pesquisa intercalada (e essa é uma das vantagens mais importantes do miniKanren sobre o Prolog padrão), é impossível encontrar uma redação rigorosa. Você não pode viver assim, decidimos e, tendo recebido uma bênção de Will, começamos a trabalhar.

Deixe-me lembrá-lo de que a semântica que desenvolvemos no estágio anterior tinha uma limitação significativa: apenas os programas com pesquisa finita foram descritos. No miniKanren, os programas em execução também são interessantes porque podem listar um número infinito de respostas. Portanto, precisávamos de uma semântica mais interessante.

Existem muitas maneiras padrão diferentes de definir a semântica de uma linguagem de programação, apenas tivemos que escolher uma delas e adaptá-la a um caso específico. Descrevemos a semântica como um sistema de transição rotulado - um conjunto de estados possíveis no processo de pesquisa e transições entre esses estados, alguns dos quais são marcados, o que significa que, nesta etapa da pesquisa, outra resposta foi encontrada. A execução de um programa em particular é determinada pela sequência de tais transições. Essas seqüências podem ser finitas (chegando ao estado terminal) ou infinitas, descrevendo simultaneamente a finalização e a não conclusão de programas. Para especificar completamente matematicamente esse objeto, é necessário usar uma definição coindutiva.

— . , (, , — ..). , miniKanren' ( ).

, , — . . ( ), , .
( ): , , , .

, , / .

Coq'a. , , «. Qed». .