🎗️ 🤞 👍 Wolfensteiny 3D - engenharia reversa 251 bytes de JavaScript 📤 🐱 🦀

Ao escrever código, muitos não pensam em outra coisa senão na lógica do próprio programa. Menos pessoas pensam em otimizar o código ao longo do tempo, a partir da memória. Mas apenas alguns atingem o último nível - compactando o programa para um tamanho pequeno recorde.

Veja, por exemplo, o resultado de apenas 251 bytes de JavaScript:

Bem, vamos descobrir como funciona!

De onde é?

Esse código, bem como o que eu abordei neste artigo, está localizado no site p01.org do magnífico Mathieu 'p01' Henri, um desenvolvedor de JavaScript e não apenas frequentemente envolvido na compactação de código para tamanhos impossíveis. O material de origem deste artigo está aqui .

Portanto, antes de você ter os 251 bytes do código fonte.

<body onload=E=c.getContext("2d"),setInterval(F="t+=.2,Q=Math.cos;c.height=300;for(x=h;x--;)for(y=h;y--;E.fillRect(x*4,y*4,bd?4:D/2,D/2))for(D=0;'.'<F[D*y/hD/2|0?1:(d=t+D*Q(T=x/h-.5+Q(t)/8)&7)|(3.5+D*Q(T-8))<<3]&&D<8;b=d)D+=.1",t=h=75)><canvas id=c>

É claro que nada está claro.

Tornando o código legível

Primeiro, coloquei todo o código JavaScript em uma tag separada, por conveniência.

Pode-se observar que as variáveis E , h , Q , F e outras são constantes que podem ser substituídas por seus próprios valores / objetos, além de alterar os nomes.

 var context = c.getContext("2d") var F="t+=.2,Q=Math.cos;c.height=300;for(x=h;x--;)for(y=h;y--;E.fillRect(x*4,y*4,bd?4:D/2,D/2))for(D=0;'.'<F[D*y/hD/2|0?1:(d=t+D*Q(T=x/h-.5+Q(t)/8)&7)|(3.5+D*Q(T-8))<<3]&&D<8;b=d)D+=.1" var t = 75 var size = 75 function render(){ t += 0.2; c.height=300; for(let x = size; x--;) for(let y = size; y--; context.fillRect(x * 4,y * 4,b - d? 4 : D / 2, D / 2)) for(var D = 0; '.' < F[D * y / size - D / 2 | 0 ? 1 : (d = t + D * Math.cos(T = x / size - 0.5 + Math.cos(t) / 8) & 7) | (3.5 + D * Math.cos(T - 8)) << 3] && D < 8; b = d) D += 0.1 } setInterval(render, 75);

Aqui, o código da string já foi retirado para a função e a própria string não foi tocada, precisaremos no futuro.

Agora converta os dois loops externos em while .

 function render(){ t += 0.2; c.height=300; let x = size; while(x > 0){ let y = size; while(y > 0){ for(var D = 0; '.' < F[D * y / size - D / 2 | 0 ? 1 : (d = t + D * Math.cos(T = x / size - 0.5 + Math.cos(t) / 8) & 7) | (3.5 + D * Math.cos(T - 8)) << 3] && D < 8; b = d) D += 0.1 context.fillRect(x * 4,y * 4,b - d? 4 : D / 2, D / 2); y--; } x--; } }

Como vemos isso?

Vamos entender por que vemos isso. Se você olhar a foto novamente, poderá entender muito.

Imagem clicável

Aqui está o que vemos:

Quanto mais distante o assunto, mais escuro é
A parte oblíqua dos obstáculos encontrados é inundada de maneira diferente por linhas, não por pontos.

No código, o desenho é refletido assim:

 // ,  ,       //   ||     // | | || | | // ↓ ↓ ↓↓ ↓ ↓ context.fillRect(x * 4,y * 4,b - d? 4 : D / 2, D / 2);

Por que vemos objetos volumétricos nessa enxurrada de pontos pretos? Afinal, precisamos nos contentar com apenas diferentes tons de preto - o tamanho dos pontos pretos (não podemos mudar a cor, o E.fillStyle é muito longo!). De fato, funciona simplesmente porque, em uma imagem bidimensional, nossos olhos se baseiam principalmente na sombra e no brilho da luz.

Imagine-se caminhando por um corredor escuro com apenas uma lanterna nas mãos. Você brilha à sua frente e vê que alguns objetos estão mais próximos e mais brilhantes (uma lanterna brilha, um obstáculo é brilhante, não há sombras), enquanto outros são mais distantes e mais escuros (a luz é dispersa, fraca e vemos a escuridão - e sentimos a distância). Então aqui - quanto mais longe o objeto (maior D ), maior em tamanho, desenhamos um quadrado preto na tela.
Mas como sabemos o que precisa ser brilhante e o que não é?

Contar o pixel

Agora vamos lidar com esse monstro:

 for(var D = 0; '.' < F[D * y / size - D / 2 | 0 ? 1 : (d = t + D * Math.cos(T = x / size - 0.5 + Math.cos(t) / 8) & 7) | (3.5 + D * Math.cos(T - 8)) << 3] && D < 8; b = d) D += 0.1

Então Toda essa expressão é um algoritmo de raymarching de passo fixo que permite encontrar a interseção da viga com os blocos. Para cada pixel da tela, lançamos um feixe e o seguimos com uma etapa fixa de 0.1 e, assim que encontramos um obstáculo, terminamos o algoritmo e desenhamos um pixel na tela, sabendo a distância do obstáculo.

Vamos começar a ler este código em partes.

Condição D * y / size - D / 2 | 0 D * y / size - D / 2 | 0 pode ser representado como

D * (f r a c y t a m a n h o - f r a c 12) = D * (f r a c y - t a m a n h o / 2 t a m a n h o) < 1

$D * (\ frac {y} {tamanho} - \ frac {1} {2}) = D * (\ frac {y - tamanho / 2} {tamanho}) <1$ , a expressão entre parênteses mostrará o "desvio" y do centro da tela (em frações da tela). Então, estamos tentando entender se a viga está entre o chão e o teto ou não. Portanto, se tocarmos o chão (ou teto), sairemos ainda mais do loop, para desenhar e desenhar um pixel.
E se não tocarmos, continuamos os cálculos: procuramos as coordenadas atuais da viga.

 var T = x / size - .5 + Math.cos(t) / 8; // Math.cos(t)   //    var xcoord = t + depth * Math.cos(T); var ycoord = 3.5 + depth * Math.cos(T - 8); //

Por que cos (T - 8)?

Então acontece que

c o s (x - 8) a p r o x s i n (x)

$cos (x-8) \ aprox sin (x)$ com uma precisão de 0,15 radianos. Tudo porque

f r a c 5 p i 2 a p r o x . 8, 15 a p r o x . 8

$\ frac {5 \ pi} {2} \ aprox. 8,15 \ aprox. 8$

e então

c o s (a l p h a - 8) a p p r o x c o s (a l p h a - f r a c 5 p i 2) = c o s (a l p h a - f r a c p i 2) = s i n (a l p h a)

$cos (\ alpha-8) \ approx cos (\ alpha- \ frac {5 \ pi} {2}) = cos (\ alpha - \ frac {\ pi} {2}) = sin (\ alpha)$

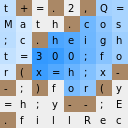
Vale a pena falar sobre como um ponto no espaço é verificado para um bloco em geral. O cartão em si é retirado do código fonte ( F ) e tem a seguinte aparência:

 t+=.2,Q= ----> ░█░█░█░░ Math.cos ----> ░░░░█░░░ ;c.heigh ----> ░░█░░░░░   - t=300;fo ----> ░░░░░░░░ <----  , r(x=h;x- ----> ░█░░░░░█     -;)for(y ----> █░█░░░█░ =h;y--;E ----> ░░░░██░░ .fillRec ----> █░░░░░░░

Assim, parece que está em movimento, o campo de visão da câmera é indicado aqui.

As células cujo código de símbolo é menor que o código de ponto - "." Estão marcadas em escuro "." - isto é, os caracteres !"#$%&'()*+,-. Agora, arredondamos as coordenadas da viga e tentamos descobrir se a letra no índice" coordenadas "é escura (obstáculo) ou não (vire a viga mais adiante).

Como o índice é um e as coordenadas são duas, usamos o hack:

 var boxIndex = xcoord & 7 | ycoord << 3;

Como resultado, obtemos um número que reflete o número do bloco (bom ou vazio).

Vamos voltar ao código. Agora ele parece decente.

O código é um pouco gordo

 function render(){ t += 0.2; c.height=300; let x = size; while(x > 0){ let y = size; while(y > 0){ var depth = 0 while(depth < 8){ depth += 0.1 var T = x / size - .5 + Math.cos(t) / 8; //   var isFloorOrCeiling = depth * y / size - depth / 2 | 0; //      ? if(isFloorOrCeiling) break; var xcoord = t + depth * Math.cos(T) & 7; var ycoord = 3.5 + depth * Math.sin(T); // cos - 8 -> sin boxIndex = xcoord | ycoord << 3; //     , //    if ('.' >= F[boxIndex]) break; b = xcoord; //  ?  ! } context.fillRect(x * 4, y * 4, b - xcoord ? 4 : depth / 2, depth / 2) y--; } x--; } }

Voltar ao desenho

Por que precisamos de tudo isso? Agora, depois de executar esse algoritmo, sabemos a distância do objeto e podemos desenhá-lo. Mas uma pergunta permaneceu sem resposta: como distinguir o teto de uma unidade separada? Afinal, a distância até o teto e o bloco são números que não são diferentes! De fato, já respondemos a essa pergunta.

 // ,  ,      // || // ↓↓ context.fillRect(x * 4, y * 4, b - xcoord ? 4 : depth / 2, depth / 2);

Há uma condição no código relacionada à variável b afetar a largura do "grande pixel preto": b - xcoord ? 4 : depth / 2 b - xcoord ? 4 : depth / 2 . Vamos remover essa condição e ver o que acontece sem ela:

Não há fronteiras entre os blocos e o teto! (clicável)

A condição b - xcoord nos dará uma largura constante quando a mudança de coordenadas é 0. E quando isso não pode acontecer? Isso não acontece apenas quando não chegamos à linha (2) no código:

 // .... var xcoord = t + depth * Math.cos(T) & 7; // <---    (1) // ... if ('.' >= F[boxIndex]) // <---    (3) break; b = xcoord; // <---     (2) // ....

Isso significa que o programa sai do ciclo mais cedo, na linha (3) , quando o feixe entra em um bloco opaco na direção quase perpendicular à sua parede, ou seja, cai na face “frontal” do bloco. Assim, todos os blocos são diferentes do piso e do teto.

Então, é assim que esta linda imagem 3D é exibida, o que não só agrada aos olhos, mas também faz você pensar como e por que ela funciona. Você pode ver esse código em ação aqui (off. Site do desenvolvedor deste milagre).

Wolfensteiny 3D - engenharia reversa 251 bytes de JavaScript

Tornando o código legível

Como vemos isso?

Contar o pixel

Voltar ao desenho

More articles: