Em 1974, o matemático britânico Roger Penrose criou um conjunto revolucionário de peças que podem ser usadas para preencher um plano infinito com um padrão que nunca se repete. Em 1982, o cristalógrafo israelense Daniel Shekhtman descobriu uma liga de metal cujos átomos estavam dispostos em uma ordem nunca antes encontrada na ciência dos materiais. Penrose alcançou reconhecimento público maciço, raramente dado a matemáticos. Shekhtman recebeu o Prêmio Nobel. Ambos os cientistas desafiaram a intuição humana e mudaram o básico da compreensão da estrutura da natureza, descobrindo que uma variabilidade infinita pode ocorrer mesmo em um ambiente altamente ordenado.
No centro de suas descobertas está uma "simetria proibida", chamada assim porque contradiz a conexão profundamente enraizada entre simetria e repetibilidade. A simetria é baseada nos eixos de reflexão - tudo o que está em um lado da linha é duplicado no outro. Em matemática, essa conexão é expressa por padrões de espaço lado a lado. Formas simétricas, como retângulos e triângulos, podem preencher o plano sem espaços e superposições, criando um padrão de repetição constante. Os padrões de repetição são chamados de "periódicos" e dizem ter "simetria de transferência". Se você mover o padrão (padrão) de um lugar para outro, ele terá a mesma aparência.
Como um cientista ousado e ambicioso, Penrose estava mais interessado não nos mesmos padrões e repetibilidade, mas na variabilidade infinita. Mais especificamente, ele estava interessado em ladrilhos "aperiódicos", isto é, conjuntos de figuras que podem preencher um plano infinito sem espaços e superposições, e o padrão de ladrilhos nunca é repetido. Essa foi uma tarefa difícil, porque ele não podia usar figuras (peças) com dois, três, quatro ou seis eixos de simetria - retângulos, triângulos, quadrados ou hexágonos - porque em um plano infinito eles criavam padrões periódicos ou repetitivos. Ou seja, ele precisava usar figuras que pensavam deixar lacunas ao preencher o avião - figuras que proibiam a simetria.
Para criar seu próprio plano de padrões não repetitivos, Penrose voltou-se para a simetria de cinco eixos - para pentágonos, em particular porque, segundo ele, é "apenas bom olhar para pentágonos". O que é notável nas figuras de Penrose é que, embora ele as tenha obtido das linhas e cantos dos retângulos, elas não deixaram lacunas feias. Eles se encaixam firmemente um no outro, dobrando e girando o avião, sempre próximos da repetibilidade, mas nunca alcançando-o.
O mosaico de Penrose conquistou a atenção do público por duas razões principais. Primeiro, ele encontrou uma maneira de gerar padrões infinitamente variáveis a partir de apenas dois tipos de formas. Em segundo lugar, seus azulejos eram figuras simples e simétricas, que por si só não mostravam sinais de propriedades incomuns.

Penrose criou várias variedades de seus conjuntos de figuras aperiódicas. Um dos mais famosos é chamado de "cobra" e "dardo". A "pipa" parece uma pipa infantil e o "dardo" parece um esboço simplificado de um bombardeiro furtivo. Ambos estão claramente divididos ao longo dos eixos de simetria e cada um deles possui arcos simétricos simples na superfície. Penrose definiu uma regra para a colocação de formas: para o posicionamento "adequado" dos ladrilhos, esses arcos devem corresponder, criando curvas inextricáveis. Sem essa regra, "cobras" e "dardos" podem ser organizados em padrões repetidos. Se você seguir esta regra, a repetição nunca ocorrerá. "Cobra" e "dardo" enchem infinitamente o avião, dançando em torno de seus cinco eixos, criando estrelas e decágonos, curvas curvas, borboletas e flores. As figuras são repetidas, mas novas variações aparecem nelas.
O professor clínico de matemática Edmund Harriss, da Universidade de Arkansas, que escreveu um doutorado sobre os azulejos de Penrose, oferece essa comparação. “Imagine que você vive em um mundo de quadrados. Você começa a andar e, quando chega ao fim da praça, a próxima é exatamente a mesma e você sabe o que verá se continuar se movendo sem parar. " Os azulejos de Penrose têm exatamente a natureza oposta. “Qualquer informação que você tenha, qualquer parte do padrão que você veja, você nunca pode prever o que acontecerá a seguir. Sempre haverá algo que você nunca viu antes.
Um dos aspectos curiosos da divisão aperiódica de um avião é que as informações de posicionamento são de alguma forma transmitidas a longas distâncias - o ladrilho Penrose, colocado em um só lugar, impede a colocação de outros ladrilhos em centenas (e também milhares e milhões) de ladrilhos. "Uma restrição local de alguma forma cria uma restrição global", diz Harriss. "Isso sugere que em nenhuma escala essas peças criarão algo periódico". Você pode optar por colocar, por exemplo, uma “cobra” em uma área ou um “dardo” em algum lugar remoto. Qualquer uma das peças serve, mas não as duas.
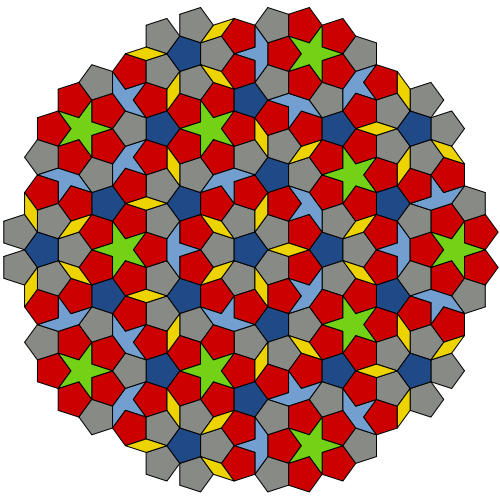
Esses ladrilhos, formando um padrão interminável e não repetitivo, expressam a proporção de Fibonacci, também conhecida como "proporção áurea". Diz-se que dois números têm uma proporção áurea se a proporção de um número menor para um maior for a mesma que a proporção de um número maior para a soma de dois números. Nesse caso, a proporção da área da "cobra" com a área do "dardo" é a proporção áurea. A proporção do lado comprido da "cobra" para o lado mais curto também é a proporção áurea.
As peças de Penrose também podem ser subdivididas em versões menores de si mesmas. Uma "cobra" consiste em duas "cobras" menores e duas metades de um "dardo". O "dardo" consiste em uma "cobra" menor e dois tapetes "dardo". (Em qualquer mosaico adequado de Penrose, essas metades dos "dardos" estão alinhadas entre si. Do ponto de vista da matemática, isso permite que elas sejam consideradas como "dardos" inteiros.)) Diz Harriss. "Se eu os subdividir, receberei 2
A +
B " cobras "e
A +
B " dardos "".
Se você fizer essa substituição um número infinito de vezes, poderá calcular a participação total de cada tipo de bloco, como se estivesse disposto em um plano infinito. Nesses cálculos, um padrão de
repetição sempre leva a um número racional. Se a proporção for um número irracional, isso significa que o padrão nunca se repetirá completamente. Nos cálculos para as peças de Penrose, não é apenas o número irracional obtido, sua proporção é a razão de Fibonacci - a proporção de "dardos" para "cobras" é igual à proporção de "cobras" para o número total de peças.
Dado que a proporção de Fibonacci é onipresente por natureza - de abacaxi a populações de coelhos - é ainda mais estranho que essa proporção seja fundamental para o sistema de ladrilhos, que, ao que parece, não tem nada a ver com o mundo físico. Penrose criou algo novo na ciência, intrigante precisamente ali, que não deveria funcionar como a natureza. Era como se Penrose tivesse escrito uma história de ficção científica sobre uma nova espécie de animal, e então o zoólogo descobriu essa espécie vivendo na Terra. De fato, as peças de Penrose estão associadas à proporção áurea, à matemática que inventamos e à matemática do mundo ao nosso redor.

Iniciando o estudo da simetria proibida, Penrose não poderia ter adivinhado que havia se tornado parte da mudança de pensamento que levou à descoberta de um novo campo da ciência matemática. Afinal, a simetria é fundamental para a matemática pura e para o mundo natural. O astrofísico Mario Livio chamou a simetria de "uma das ferramentas mais necessárias para decifrar a estrutura da natureza". A natureza usa quadrados e hexágonos pela mesma razão que os seres humanos: eles são simples, eficientes e ordenados. Se os pentágonos pareciam impraticáveis, mesmo para uma tarefa tão simples como o preenchimento de pisos em design de interiores, acreditava-se que eles não podiam ser usados para criar átomos em materiais sólidos, como cristais.
Os cristais consistem em redes tridimensionais de átomos. Os cristais crescem adicionando novos átomos e expandindo as redes. Isso acontece com mais eficiência quando os átomos se alinham em padrões repetidos. Por décadas, a história terminou aí: os cristais estavam repetindo estruturas. O ponto.
Mas então, em 1982, Shekhtman saiu de licença criativa da Universidade Technion em Haifa e começou a trabalhar no Departamento Nacional de Padrões. Ele se atrapalhou em um laboratório de ligas de alumínio e manganês. Os padrões de difração criados por suas estruturas cristalinas não pareciam se assemelhar a nenhuma das simetrias padrão conhecidas pelos cristalógrafos. De fato, os átomos alinhados nos próprios pentágonos, losangos, "cobras" e "dardos" que Penrose descobriu no mundo da matemática.
"É claro que eu estava familiarizado com os azulejos da Penrose", diz Schechtman. Mas ele não tinha motivos para suspeitar da conexão deles com essa liga. “Eu não entendi o que é. Nos meses seguintes, repeti minhas experiências repetidas vezes. No final das minhas férias criativas, eu sabia exatamente o que não era, mas ainda não fazia ideia do que era. ”
Para entender o que ele descobriu, Schechtman, como Penrose, teve que questionar suas idéias intuitivas habituais. Ele teve que aceitar a simetria proibida e sua confusão pentagonal com uma falta de repetibilidade. Enquanto estava em Israel, ele relutou em reconhecer que havia descoberto uma estrutura atômica cristalina não repetitiva. No entanto, ninguém no mundo da ciência dos materiais poderia, a princípio, atribuir essa descoberta aos cristais. Portanto, eles foram chamados de "quase-cristais".
A matemática bizarra de Penrose parecia ter surgido no mundo natural. "Por 80 anos, os cristais foram definidos como estruturas" ordenadas e periódicas ", porque todos os cristais que estudamos desde 1912 eram periódicos", explica Schechtman. “Somente em 1992 a União Internacional de Cristalógrafos organizou um comitê para selecionar uma nova definição para a palavra cristal. Essa nova definição é uma mudança de paradigma para a cristalografia. ”
Não foi apenas a simples inércia do pensamento que impediu a compreensão e a aceitação de Shekhtman da descoberta. As estruturas cristalinas aperiódicas não eram apenas desconhecidas - elas eram consideradas não naturais. Lembre-se de que a localização de um bloco Penrose pode afetar as formas dos milhares de blocos - as restrições locais criam as globais. Mas se um cristal é formado átomo por átomo, não deve haver uma lei da natureza que crie as restrições inerentes às peças de Penrose.
Descobriu-se que os cristais nem sempre formam átomo por átomo. “Em compostos intermetálicos muito complexos, os elementos são enormes. Eles não são locais ”, diz Schechtman. Quando grandes fragmentos de cristal são formados ao mesmo tempo, e não pelo crescimento gradual de átomos, os átomos localizados muito longe um do outro podem influenciar a posição mútua, como nos ladrilhos Penrose.
Como é o caso de muitos tabus, a simetria proibida foi reconhecida como uma das formas aceitáveis de existência na natureza. Os quasicristais não apenas se tornaram um objeto de estudo em um novo campo de pesquisa científica: descobriu-se que eles têm muitas propriedades úteis que surgem devido à sua estrutura incomum. Por exemplo, sua configuração assimétrica de átomos lhes fornece baixa energia superficial, isto é, pouco pode aderir a eles. Assim, revestimentos quase cristalinos começaram a ser utilizados em utensílios de cozinha antiaderentes. (Quando Penrose criou seus novos ladrilhos, ele não podia imaginar que eles seriam usados na cristalografia, sem mencionar a fritura de ovos.) Além disso, os quase-cristais geralmente têm baixo atrito e desgaste, por isso são revestimentos ideais para máquinas de barbear e cirúrgicas. instrumentos ou quaisquer outros instrumentos afiados relacionados ao corpo humano.

Como as estruturas quase-cristalinas nunca são repetidas, elas criam padrões de difração exclusivos de radiação eletromagnética. Pesquisadores fotônicos estão interessados em como eles afetam a transmissão de luz, refletividade e fotoluminescência. Se forem resfriados, sua resistência elétrica cai para quase zero nível. Mas eles também absorvem a radiação infravermelha e aquecem muito rapidamente a altas temperaturas. Por esse motivo, elas se tornam uma adição muito útil às impressoras 3D, nas quais o pó de plástico é usado como material de partida. Shekhtman explica: se um pó quasiperiódico é misturado com ele e exposto à radiação infravermelha, o pó quasiperiódico "esquenta muito rapidamente e derrete as partículas plásticas circundantes, o que as faz grudar".
Ninguém sabe como termina a história da simetria proibida. Os matemáticos continuam a explorar as propriedades dos ladrilhos Penrose. Os quase-cristais continuam sendo objeto de estudo tanto na pesquisa fundamental quanto na aplicada. Mas até agora essa jornada tem sido incrível. Nos últimos 40 anos, a simetria de cinco eixos passou de impraticável para valiosa, de antinatural para completamente natural, de proibida para dominante. E por essa transformação, devemos agradecer a dois cientistas que abandonaram suas idéias habituais para descobrir uma nova e extraordinária forma de infinitas variações da natureza.
Sobre o autor: Patchen Bars é um jornalista e autor baseado em Toronto. Atualmente, ele está trabalhando em um livro sobre a relação entre a matemática pura e o mundo natural.