Fractais em números irracionais

Este artigo é uma continuação do meu primeiro artigo , Fractals in Prime Numbers .

Próximo artigo: Fractais em números irracionais. Parte 2



Em um artigo anterior, aprendemos a desenhar padrões auto-semelhantes usando números primos entre si. Neste artigo, mostrarei a natureza fractal do número $$$\ sqrt {2}$.
Sem um prefácio. Sob gato.

Definiremos terminologia e notação. Em matemática, os sistemas descritos abaixo são chamados de bilhar . Além disso, usaremos esse termo. As dimensões dos bilhar retangulares serão indicadas por $$$M$(largura) e $$$N$(altura).

Bilhar binário

No artigo anterior, pegamos um bilhar retangular com lados $$$M$e $$$N$, lançou uma bola e marcou a trajetória com uma linha tracejada através da célula:



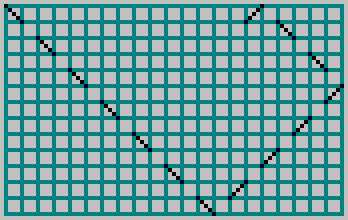
Para mutuamente simples $$$M$e $$$N$nós obtemos o padrão:



Na versão binária, marcamos a trajetória não com uma linha tracejada, mas preenchendo alternadamente as células com preto e branco (formamos uma matriz binária, colocamos 0 para preto e 1 para branco na célula correspondente):



Regras de reflexão de borda:



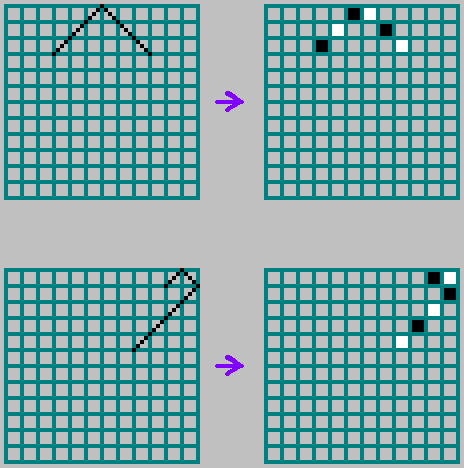
Para mutuamente simples $$$M$e $$$N$a trajetória passa por cada célula:




Se as partes tiverem um divisor comum, a bola entra no canto antes de passar por cada célula:



É conveniente considerar este caso como bilhar em um retângulo com lados $$$\ frac {M} {GCD}$e $$$\ frac {N} {GCD}$(GCD é o maior fator comum):



Antes de prosseguir , preencha a tabela proposta pelo usuário Captain1312 em seu artigo (dividiremos os lados do bilhar em GCD).

$$$(1, 0)$um pouco

Para cada mesa de bilhar $$$M$e $$$N$demorar um pouco com coordenadas $$$(1, 0)$.



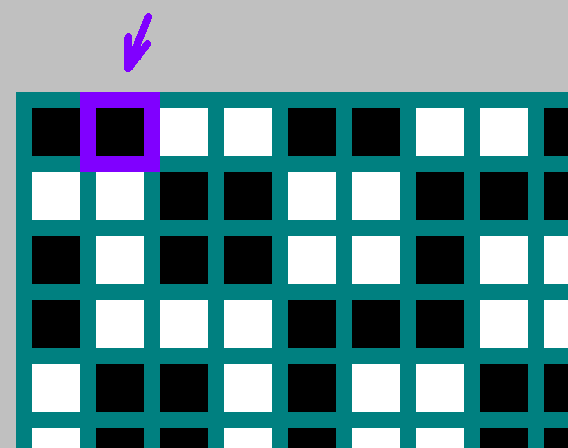
Se $$$M$é um divisor $$$N$- então um pouco com coordenadas $$$(1, 0)$ausente ( $$$\ frac {M} {GCD} = 1$) Nesse caso, pegamos o bit invertido com as coordenadas $$$(0, 1)$.

Preencha a tabela. A origem é o canto superior esquerdo. Por $$$x$- largura dos bilhares $$$M$por $$$y$- altura $$$N$. Para cada bilhar marcamos um pouco $$$(1, 0)$ou bit invertido $$$(0, 1)$(retornaremos a este tópico abaixo).

Sequência binária

Por que invertemos o bit quando a largura dos bilhares $$$M = 1$? Para mutuamente simples $$$M$e $$$N$, a trajetória da bola passa por cada célula. Entre as paredes superior e esquerda do bilhar, a bola passa a cada vez um número par de células.





Os bits na coluna da esquerda são os bits invertidos da linha superior. Não aceitamos o zero - a trajetória começa com ele:



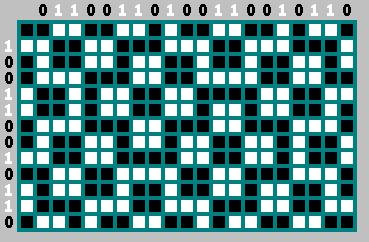
Além disso, podemos remover com segurança cada segundo bit dessa sequência (bit $$$2_ {n-1}$- bit invertido $$$2_ {n}$):



Tem a sequência $$ para bilhar $$$(21,13)$. A sequência é exclusiva para todos. $$$M$e $$$N$.

Qualquer altura $$$N$nós não pegamos - a bola sempre segue a trajetória $$$2N$entre duas reflexões da parede superior. Na parede superior, o movimento sempre começa com um bit "0" (célula preta) e termina com um bit "1" (célula branca):



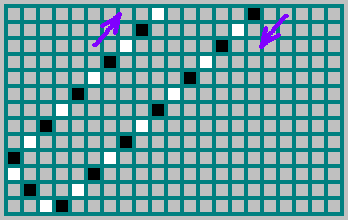
De fato, a sequência (que destacamos acima - $$ ) mostra de que lado a bola voou: 1 - se a bola voou, refletida na parede direita e 0 - se a bola voou, refletida na parede esquerda. Na figura, a trajetória da bola é marcada em preto se a bola se moveu para a direita e branca se se move para a esquerda:




Esta sequência ( $$ ) contém todas as informações necessárias sobre o padrão. Com ele, podemos restaurar o padrão original (e até olhar além da borda inferior do padrão). Pegue um quadrado com os lados $$$M$. Organizamos os bits de nossa sequência nos locais em que a bola bate na parede superior (a distância entre os toques adjacentes da bola é de 2 células).



Se o bit correspondente = 1 - começamos a mover para a esquerda, marcando a trajetória através da célula. Se bit = 0 - mova para a direita.



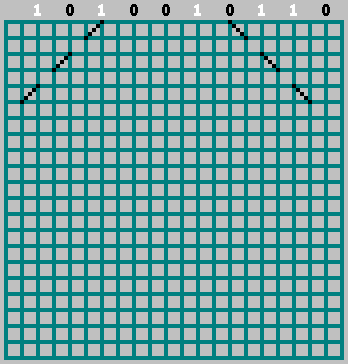
Nesse caso, não esqueça o bit zero:



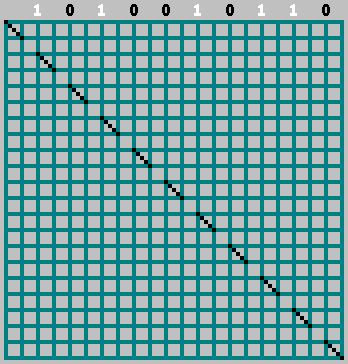
Gif:



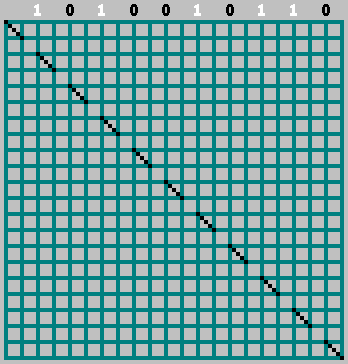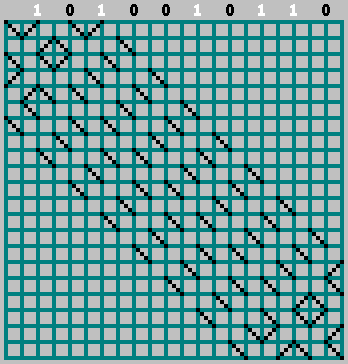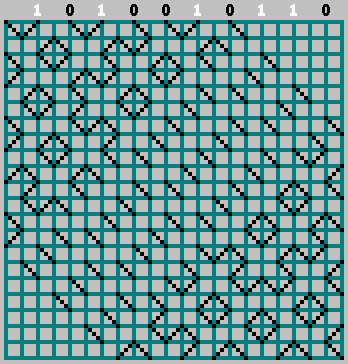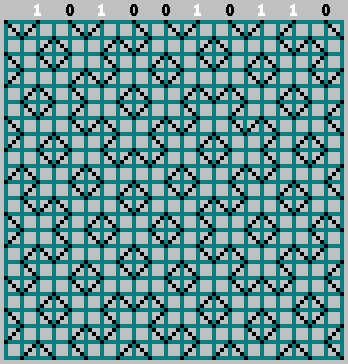
Obtivemos o padrão original (e parecíamos um pouco além da borda inferior):



Script para visualizar sequências binárias

Podemos construir essa sequência usando o restante da divisão.

Bilhar unidimensional

No eixo numérico $$$X$pegue dois pontos: $$$0$e $$$M$.



Movendo-se de um ponto para outro, meça a distância $$$N$:



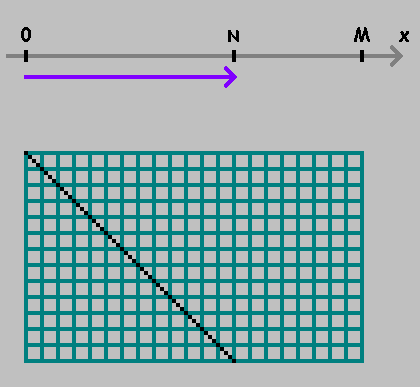
Marcou o ponto. Continuamos a medir a distância a partir deste ponto, mantendo a direção. Se você chegou ao ponto $$$0$ou $$$M$- mudar de direção:



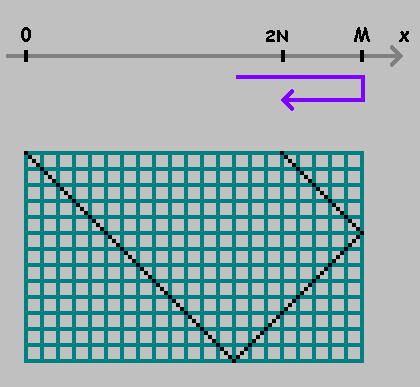
Como pode ser visto nas figuras acima, o primeiro ponto mostra o local em que a bola toca a parede inferior do bilhar. Este ponto não nos interessa. Nós só vamos consertar pontos $$$2kN$para $$$k = 0,1,2, ...$.

Como marcar esses pontos? Vire nossos bilhar no eixo $$$X$. Marque os pontos $$$0, M, 2M, 3M, ...$. Agora chegando ao ponto $$$M$não mudamos a direção do movimento, mas continuamos a ir ao ponto $$ .



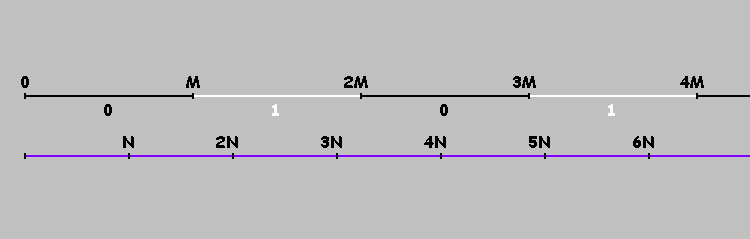
Múltiplos $$$M$, divida nosso eixo em segmentos. Marcamos condicionalmente esses segmentos com uns e zeros (alternados). Nos segmentos marcados com zeros, a bola (em um bilhar retangular) se move da esquerda para a direita. Nos segmentos marcados com unidades - da direita para a esquerda. Ou mais simples: a bola se move da esquerda para a direita se $$$Q_k = 0$para

$$

$$Q_k = \ lfloor \ frac {2kN} {M} \ rfloor \; (\ textrm {mod} \; 2); \ quad k = 0,1,2, ...$$

(Atenção especial deve ser dada a esta fórmula. A seguir, retornaremos a ela)

É fácil ver que o ponto em que a bola tocou a parede superior do bilhar é o restante da divisão $$$2kN$em $$$M$. Nesse caso, não podemos fixar o movimento da bola na direção oposta. Tomamos toda a parte da divisão $$$2kN$em $$$M$se for par - consideramos o restante da divisão $$$2kN$em $$$M$. Divida o restante resultante por 2 (a distância entre pontos de contato adjacentes é de duas células). Obteve os índices dos elementos da matriz, que precisamos preencher com zeros. Os demais elementos são preenchidos com unidades (a bola se move da parede direita para a esquerda).

Comprimento da sequência = $$$\ frac {M} {2}$.

function sequence(m,n){ var md=m/2; var array=[]; for(var k=0;k<md;k++) array[k]=1; for(var k=0;k<md;k++) if(Math.floor(2*k*n/m)%2==0) array[((2*k*n)%m)/2]=0; return array; } console.log(sequence(55, 34).join('')); // -> 0101001011010010110101101001 

Agora podemos construir uma sequência binária para bilhar com qualquer lado $$$M$e $$$N$(por números naturais).
Alguns exemplos:
144x89 (números de Fibonacci):
010100101101001011010110100101101001010010110100101101011010010110100101

169x70 (números de Pell):
0101011010100101011010100101011010110101001010110101001010110101001010010101101010010

233x55 (números ímpares de Fibonacci $$$F_n$e $$$F_ {n-3}$):
0100100110110110010011011011001001001101100100100110110010010011011011001001101101100
10010011011001001001101100100100


Nós temos sequências. De que outra forma você pode visualizar sequências binárias? Usando gráficos da tartaruga .

Gráficos de tartaruga

Desenhe uma linha. Em seguida, pegamos alternadamente os bits da nossa sequência. Se bit = 1 - gire o segmento em relação ao anterior $$$60 ^ {\ circ}$(sentido horário). Se bit = 0 - gire o segmento $$$-60 ^ {\ circ}$. O início do próximo segmento é o fim do anterior.



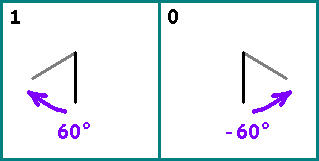
Tome dois números de Fibonacci grandes o suficiente: $$$F_ {29} = 514229$e $$$F_ {28} = 317811$.

Construiu a sequência:
00101101001011010010100101101001011010110100101101001010010110100101 ... (257114 caracteres mais zero bits).

Nós visualizamos usando gráficos de tartarugas. O tamanho do segmento inicial é de 10 pixels (o segmento inicial no canto inferior direito):



O tamanho do segmento inicial é de 5 pixels:



O tamanho do segmento inicial é de 1 pixel:



O próximo exemplo são os números de Pell.

$$

$$P_n = \ begin {cases} 0, n = 0; \\ 1, n = 1 \\ 2P_ {n-1} + P_ {n-2}, n> 1 \ end {cases}$$

Tome $$$P_ {16} = 470832$e $$$P_ {15} = 195025$.

Sequência:
0010100101011010100101011010100101001010110101001010110101000010101101 (235415 caracteres mais bit zero).

O tamanho do segmento inicial é de 1 pixel:



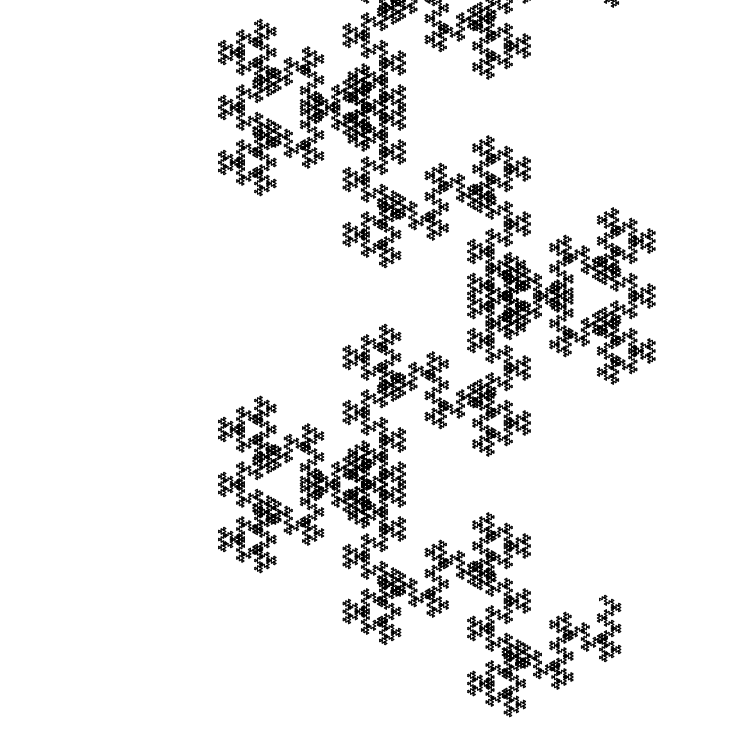
Outro exemplo são números ímpares de Fibonacci $$$F_n$e $$$F_ {n-3}$.
Tome $$$F_ {28} = 317811$e $$$F_ {25} = 75025$.
Sequência:
00110110010010011111001001001001101101100100110110110010010011011011001001 ... (158905 mais zero bit).
Em vez de cantos $$$60 ^ {\ circ}$e $$$-60 ^ {\ circ}$vamos usar os cantos $$$90 ^ {\ circ}$e $$$-90 ^ {\ circ}$.
O tamanho do segmento inicial é de 5 pixels:



O tamanho do segmento inicial é de 0,4 pixels:



Esta curva tem um nome - " palavra fractal de Fibonacci ". A dimensão Hausdorff para esta curva é conhecida:

$$

$$D = 3 {\ frac {\ log \ Phi} {\ log (1 + {\ sqrt {2}})}} = 1,6379; \ quad \ Phi = \ frac {1 + {\ sqrt {5}}} {2}$$

Script para visualizar seqüências binárias usando Turtle Graphics

O problema

É possível desenhar um padrão para bilhar, cujos lados são incomensuráveis ​​(um dos lados é um número irracional)? A tarefa não é trivial. Tentando resolver esse problema, enfrentaremos várias perguntas:

1. Se as partes são incomensuráveis ​​- não podemos pavimentar os bilhares com células do mesmo tamanho.
2. Se os lados forem incomensuráveis ​​- a bola será refletida infinitamente e nunca atingirá o canto.
3. Sequências de bilhar são preenchidas não em ordem, mas aleatoriamente.



As duas primeiras perguntas, obviamente, não têm solução. Mas se houvesse uma maneira de preencher a sequência em ordem, poderíamos, movendo a sequência da esquerda para a direita, restaurar o padrão da maneira que usamos acima. E assim, ver como o padrão fica no canto superior esquerdo dos bilhar, cujos lados são incomensuráveis.

Magia negra

Tome bilhar, cujos lados são iguais aos números de Fibonacci (com outros números, esse truque pode não funcionar). Coloque a bola nela e fixe o número da bola tocando na parede superior. Preencha os números com branco - se a bola se mover da direita para a esquerda e preto - se a bola se mover da esquerda para a direita:



A cor branca corresponde a uma na sequência, preto - zero. Agora vamos organizar os números em ordem:



Temos exatamente a mesma sequência de uns e zeros.


De fato, em alguns casos, não precisamos pegar o restante da divisão. Para números de Fibonacci, basta verificar a paridade da parte inteira da divisão $$$2kN$em $$$M$:

$$

$$Q_k = \ piso \ frac {2kN} {M} \ piso \; (\ textrm {mod} \; 2); \ quad k = 0,1,2, ...$$

No numerador, temos $$$F_ {n}$. No denominador - $$$F_ {n + 1}$.

Como você sabe:

$$

$$\ lim_ {n \ to \ infty} \ frac {F_n} {F_ {n + 1}} = \ frac {1} {\ Phi}$$

$$$\ Phi$- A proporção áurea. Número irracional. Agora podemos escrever nossa fórmula como:

$$

$$Q_k = \ lfloor \ frac {2k} {\ Phi} \ rfloor \; (\ textrm {mod} \; 2); \ quad k = 0,1,2, ...$$

Temos uma fórmula com a qual podemos preencher a sequência de bilhar em ordem, cuja largura é igual a $$$\ Phi$e altura $$$1$. Comprimento da sequência = $$$\ infty$, mas podemos restaurar parte do padrão, movendo-se da esquerda para a direita em sequência e olhando para o canto superior esquerdo da mesa de bilhar. Resta descobrir como contar $$$\ Phi$

A unidade dividida pela proporção áurea pode ser reescrita como:

$$

$$\ frac {1} {\ Phi} = \ frac {-1 + {\ sqrt {5}}} {2}$$

Podemos nos livrar de dois:

$$

$$\ frac {2k} {\ Phi} = \ frac {2k (-1 + {\ sqrt {5}})} {2} = k \ sqrt {5} -k$$

Nossa fórmula assume a forma:

$$

$$Q_k = \ lfloor k \ sqrt {5} -k \ rfloor \; (\ textrm {mod} \; 2); \ quad k = 0,1,2, ...$$

Para maior clareza, desenhei uma mesa. Na terceira coluna, descartamos a parte fracionária e deixamos o todo. Na quarta coluna, verificamos a paridade da parte inteira:



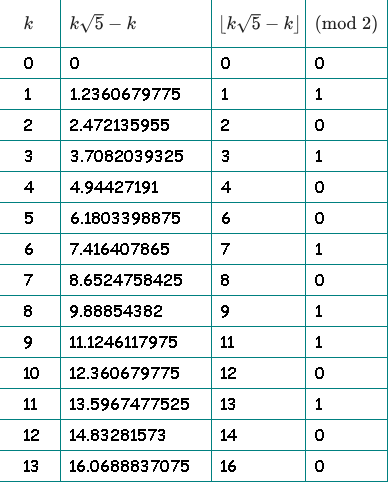
Na quarta coluna, temos nossa sequência: 01010010110100 ...

Continuamos a calcular os bits para o resto $$$k$. Restaurando parte do padrão de bilhar com lados $$$1$e $$$\ Phi$:



Se você não tira o tempo todo $$$k$- então cada segundo bit na sequência é invertido. Temos a fórmula geral:

$$

$$Q_k = \ lfloor k \ sqrt {x} \ rfloor \; (\ textrm {mod} \; 2); \ quad k = 0,1,2, ...$$

O que nos impede de usar a raiz quadrada de três ou, digamos, de dois, em vez da raiz quadrada de cinco? Nada.

Construímos uma sequência para $$$k \ sqrt {3} + k$

 var x=3; var q=[]; for(var k=0;k<256000;k++) q[k]=Math.floor(k*Math.sqrt(x)+k)%2; 

Os primeiros bits da sequência:
00100101101001001011010010110110100101101001001011010010010110100101 ...

Vamos visualizar usando gráficos de tartarugas. Ângulos de 90 e -90 graus. O tamanho inicial do segmento é de 5 pixels:



O tamanho do segmento inicial é de 0,5 pixels:



Construímos uma sequência para $$$k \ sqrt {2}$

 var x=2; var q=[]; for(var k=0;k<256000;k++) q[k]=Math.floor(k*Math.sqrt(x))%2; 

Os primeiros bits da sequência ( A083035 ):
01001101100100110010011011001101100100110110011011001001100100110110 ...

Ângulos de 90 e -90 graus. O tamanho inicial do segmento é de 5 pixels:



O tamanho do segmento inicial é de 0,5 pixels:





Ângulos de 60 e -60 graus. O tamanho inicial do segmento é de 5 pixels:



Script de visualização

Alguém pode duvidar que a paridade da parte inteira de $$$k \ sqrt {2}$dá uma sequência fractal. Visualizamos parte dessa sequência da segunda maneira:



Para maior clareza, pintei a curva mais longa no padrão resultante:



Esta curva tem um nome - "palavra fractal de Fibonacci".

Como obter essa sequência usando bilhar? Pegamos bilhar, cuja largura = 1 e altura = $$$\ sqrt {2}$. Nos limites superior e inferior, fixamos a direção do movimento da bola. Se a bola se moveu da esquerda para a direita - escreva 0, se da direita para a esquerda - escreva 1.



Dois gráficos:

$$

$$z = \ lfloor y \ sqrt {x} \ rfloor \; (\ textrm {mod} \; 2)$$

$$

$$z = \ lfloor yx \ sqrt {2} \ rfloor \; (\ textrm {mod} \; 2)$$

Você pode continuar nessa linha por muito tempo - os padrões têm muitas propriedades interessantes. Mas o artigo já era muito pesado. Vou contar sobre uma das propriedades interessantes no final.