
Durante o desenvolvimento do
meshoptimizer , surge a pergunta: "Esse algoritmo pode usar SIMD?"
A biblioteca é orientada para o desempenho, mas o SIMD nem sempre oferece vantagens significativas de velocidade. Infelizmente, o SIMD pode tornar o código menos portátil e menos sustentável. Portanto, em cada caso, é necessário buscar um compromisso. Quando o desempenho é fundamental, é necessário desenvolver e manter implementações SIMD separadas para os conjuntos de instruções SSE e NEON. Em outros casos, você precisa entender qual é o efeito do uso do SIMD. Hoje tentaremos acelerar o simplificador de malha superficial, um novo algoritmo recentemente adicionado à biblioteca, usando os conjuntos de instruções SSEn / AVXn.
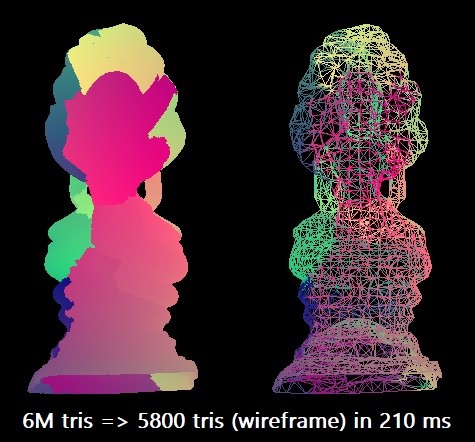
Para nossa referência, simplificamos o modelo do Buda tailandês de 6 milhões de triângulos para 0,1% desse número. Usamos o compilador Microsoft Visual Studio 2019 para a arquitetura x64 de destino. O algoritmo escalar pode executar essa racionalização em aproximadamente 210 ms em um único segmento Intel Core i7-8700K (a ~ 4,4 GHz). Isso corresponde a aproximadamente 28,5 milhões de triângulos por segundo. Talvez isso seja suficiente na prática, mas eu estava curioso para explorar as capacidades máximas do equipamento.
Em alguns casos, o procedimento pode ser paralelo dividindo a grade em partes, mas, para isso, é necessário realizar uma análise adicional da conectividade para manter os limites; portanto, por enquanto, nos restringiremos às otimizações puramente do SIMD.
Sete medições
Para entender as possibilidades de otimização, realizaremos a criação de perfil usando o Intel VTune. Execute o procedimento 100 vezes para garantir que haja dados suficientes.

Aqui, ativei o modo de microarquitetura para fixar o tempo de execução de cada função, além de encontrar gargalos. Vemos que a racionalização é realizada usando um conjunto de funções, cada uma das quais requer um certo número de ciclos. A lista de funções é classificada por tempo. Aqui estão eles em ordem de execução para facilitar a compreensão do algoritmo:
rescalePositions normaliza as posições de todos os vértices em um único cubo para se preparar para quantização usando computeVertexIdscomputeVertexIds calcula um identificador quantificado de 30 bits para cada vértice em uma grade uniforme de um determinado tamanho, em que cada eixo é quantizado em uma grade (tamanho da grade 10 bits, portanto, o identificador é 30)countTriangles calcula o número aproximado de triângulos que o inovador criará para um determinado tamanho de grade, assumindo a união de todos os vértices em uma célula da gradefillVertexCells preenche uma tabela que fillVertexCells todos os vértices para as células correspondentes; todos os vértices com o mesmo ID correspondem a uma célulafillCellQuadrics preenche a estrutura Quadric (matriz simétrica Quadric ) de cada célula para refletir informações agregadas sobre a geometria correspondentefillCellRemap calcula o índice de vértices para cada célula, escolhendo um dos vértices nessa célula e minimiza a distorção geométricafilterTriangles exibe o conjunto final de triângulos de acordo com as tabelas de vértice-célula-vértice construídas anteriormente; a tradução ingênua pode produzir uma média de aproximadamente 5% de triângulos duplicados; portanto, a função filtra as duplicatas.
computeVertexIds e
countTriangles são executados várias vezes: o algoritmo determina o tamanho da grade para mesclar vértices, realizando uma pesquisa binária acelerada para atingir o número alvo de triângulos (no nosso caso 6000) e calcula o número de triângulos que cada tamanho de grade gerará a cada iteração. Outras funções são iniciadas uma vez. Em nosso arquivo, cinco passes de pesquisa fornecem um tamanho de malha de destino de 40
3 .
O VTune relata com presteza que a função que mais consome recursos é a que calcula os quadráticos: leva quase metade do tempo total de execução de 21 s. Este é o primeiro objetivo para otimizar o SIMD.
SIMD peça por peça
Vamos dar uma olhada no código fonte do
fillCellQuadrics para entender melhor o que exatamente ele calcula:
static void fillCellQuadrics(Quadric* cell_quadrics, const unsigned int* indices, size_t index_count, const Vector3* vertex_positions, const unsigned int* vertex_cells) { for (size_t i = 0; i < index_count; i += 3) { unsigned int i0 = indices[i + 0]; unsigned int i1 = indices[i + 1]; unsigned int i2 = indices[i + 2]; unsigned int c0 = vertex_cells[i0]; unsigned int c1 = vertex_cells[i1]; unsigned int c2 = vertex_cells[i2]; bool single_cell = (c0 == c1) & (c0 == c2); float weight = single_cell ? 3.f : 1.f; Quadric Q; quadricFromTriangle(Q, vertex_positions[i0], vertex_positions[i1], vertex_positions[i2], weight); if (single_cell) { quadricAdd(cell_quadrics[c0], Q); } else { quadricAdd(cell_quadrics[c0], Q); quadricAdd(cell_quadrics[c1], Q); quadricAdd(cell_quadrics[c2], Q); } } }
A função itera sobre todos os triângulos, calcula um quadriculado para cada um deles e o adiciona aos quadricíclicos de cada célula. Quadric - uma matriz simétrica 4 × 4, apresentada como 10 números de ponto flutuante:
struct Quadric { float a00; float a10, a11; float a20, a21, a22; float b0, b1, b2, c; };
O cálculo de um quadriculado requer a solução da equação do plano para um triângulo, a construção de uma matriz quadrática e a pesagem usando a área do triângulo:
static void quadricFromPlane(Quadric& Q, float a, float b, float c, float d) { Q.a00 = a * a; Q.a10 = b * a; Q.a11 = b * b; Q.a20 = c * a; Q.a21 = c * b; Q.a22 = c * c; Q.b0 = d * a; Q.b1 = d * b; Q.b2 = d * c; Qc = d * d; } static void quadricFromTriangle(Quadric& Q, const Vector3& p0, const Vector3& p1, const Vector3& p2, float weight) { Vector3 p10 = {p1.x - p0.x, p1.y - p0.y, p1.z - p0.z}; Vector3 p20 = {p2.x - p0.x, p2.y - p0.y, p2.z - p0.z}; Vector3 normal = { p10.y * p20.z - p10.z * p20.y, p10.z * p20.x - p10.x * p20.z, p10.x * p20.y - p10.y * p20.x }; float area = normalize(normal); float distance = normal.x*p0.x + normal.y*p0.y + normal.z*p0.z; quadricFromPlane(Q, normal.x, normal.y, normal.z, -distance); quadricMul(Q, area * weight); }
Parece que existem muitas operações de ponto flutuante, para que possam ser paralelizadas usando o SIMD. Primeiro, representamos cada vetor como um vetor SIMD de
Quadric e também
Quadric estrutura
Quadric para 12 números de ponto flutuante em vez de 10 para que ele se encaixe exatamente em três registros SIMD (aumentar o tamanho não afeta o desempenho) e alteramos a ordem dos campos para que os cálculos
quadricFromPlane tornou-se mais uniforme:
struct Quadric { float a00, a11, a22; float pad0; float a10, a21, a20; float pad1; float b0, b1, b2, c; };
Aqui, alguns cálculos, em particular o produto escalar, não são muito consistentes com as versões anteriores do SSE. Felizmente, uma instrução para um produto escalar apareceu no SSE4.1, o que é muito útil para nós.
static void fillCellQuadrics(Quadric* cell_quadrics, const unsigned int* indices, size_t index_count, const Vector3* vertex_positions, const unsigned int* vertex_cells) { const int yzx = _MM_SHUFFLE(3, 0, 2, 1); const int zxy = _MM_SHUFFLE(3, 1, 0, 2); const int dp_xyz = 0x7f; for (size_t i = 0; i < index_count; i += 3) { unsigned int i0 = indices[i + 0]; unsigned int i1 = indices[i + 1]; unsigned int i2 = indices[i + 2]; unsigned int c0 = vertex_cells[i0]; unsigned int c1 = vertex_cells[i1]; unsigned int c2 = vertex_cells[i2]; bool single_cell = (c0 == c1) & (c0 == c2); __m128 p0 = _mm_loadu_ps(&vertex_positions[i0].x); __m128 p1 = _mm_loadu_ps(&vertex_positions[i1].x); __m128 p2 = _mm_loadu_ps(&vertex_positions[i2].x); __m128 p10 = _mm_sub_ps(p1, p0); __m128 p20 = _mm_sub_ps(p2, p0); __m128 normal = _mm_sub_ps( _mm_mul_ps( _mm_shuffle_ps(p10, p10, yzx), _mm_shuffle_ps(p20, p20, zxy)), _mm_mul_ps( _mm_shuffle_ps(p10, p10, zxy), _mm_shuffle_ps(p20, p20, yzx))); __m128 areasq = _mm_dp_ps(normal, normal, dp_xyz);
Não há nada particularmente interessante nesse código; estamos usando abundantemente instruções de carregamento / armazenamento desalinhadas. Embora a entrada do Vector3 possa ser alinhada, parece não haver uma penalidade perceptível para leituras desalinhadas. Observe que na primeira metade dos vetores de função não são usados, o que é bom - nossos vetores têm três componentes e, em alguns casos, apenas um (consulte cálculo de áreasq / área / distância), enquanto o processador realiza 4 operações em paralelo. De qualquer forma, vamos ver como a paralelização ajudou.

Agora, centenas de partidas do
fillCellQuadrics executadas em 5,3 s em vez de 9,8 s, o que economiza cerca de 45 ms em cada operação - nada mal, mas não muito impressionante. Em muitas instruções, usamos três em vez de quatro componentes, bem como multiplicação precisa, o que fornece um atraso bastante significativo. Se você escreveu anteriormente instruções para o SIMD, sabe como executar o produto escalar corretamente.
Para fazer isso, você precisa fazer quatro vetores de uma só vez. Em vez de armazenar um vetor completo em um registro SIMD, usamos três registros - em um armazenamos quatro componentes de
x , no outro, armazenamos
e no terceiro
z . Aqui são necessários quatro vetores para trabalhar ao mesmo tempo: significa que processaremos quatro triângulos simultaneamente.
Temos muitas matrizes com indexação dinâmica. Geralmente, ajuda a transferir dados para matrizes preparadas de componentes
x /
y /
z (ou melhor, pequenos registros SIMD são geralmente usados, por exemplo,
float x[8], y[8], z[8] , para cada um dos 8 vértices na entrada data: isso é chamado de AoSoA (matrizes de estruturas de matriz) e oferece um bom equilíbrio entre a localidade do cache e a facilidade de carregamento nos registros SIMD), mas aqui a indexação dinâmica não funciona muito bem; portanto, carregue os dados para quatro triângulos como de costume e transponha os vetores usando um conveniente macro
_MM_TRANSPOSE .
Teoricamente, você precisa calcular cada componente de quatro quadríceps finitos em seu próprio registro SIMD (por exemplo, teremos
__m128 Q_a00 com quatro componentes de
a00 finitos). Nesse caso, as operações nos quadráticos se encaixam muito bem nas instruções SIMD de 4 amplas, e a conversão realmente reduz o código - portanto, transpomos apenas os vetores iniciais e depois transpomos as equações do plano de volta e executamos o mesmo código que usamos para calcular os quadráticos, mas repita-os quatro vezes Aqui está o código que calcula as equações do plano (as partes restantes são omitidas por questões de brevidade):
unsigned int i00 = indices[(i + 0) * 3 + 0]; unsigned int i01 = indices[(i + 0) * 3 + 1]; unsigned int i02 = indices[(i + 0) * 3 + 2]; unsigned int i10 = indices[(i + 1) * 3 + 0]; unsigned int i11 = indices[(i + 1) * 3 + 1]; unsigned int i12 = indices[(i + 1) * 3 + 2]; unsigned int i20 = indices[(i + 2) * 3 + 0]; unsigned int i21 = indices[(i + 2) * 3 + 1]; unsigned int i22 = indices[(i + 2) * 3 + 2]; unsigned int i30 = indices[(i + 3) * 3 + 0]; unsigned int i31 = indices[(i + 3) * 3 + 1]; unsigned int i32 = indices[(i + 3) * 3 + 2];
O código ficou um pouco mais longo: agora processamos quatro triângulos em cada iteração e não precisamos mais das instruções SSE4.1 para isso. Em teoria, as unidades SIMD devem ser usadas com mais eficiência. Vamos ver como isso ajudou.

Ok, tudo bem. O código acelerou muito levemente, embora a função
fillCellQuadrics agora execute quase duas vezes mais rápido que a função original sem SIMD, mas não está claro se isso justifica um aumento significativo na complexidade. Teoricamente, você pode usar o AVX2 e processar 8 triângulos por iteração, mas aqui você precisará girar o loop manualmente (idealmente, todo esse código é gerado usando o ISPC, mas minhas tentativas ingênuas de fazê-lo gerar um bom código não foram bem-sucedidas: em vez de carregar / armazenar sequências ele emitiu persistentemente uma coleta / dispersão, o que diminui significativamente a execução). Vamos tentar outra coisa.
AVX2 = SSE2 + SSE2
O AVX2 é um conjunto de instruções ligeiramente idiossincrático. Possui registradores de ponto flutuante de 8 largos e uma instrução pode executar 8 operações; mas, de fato, essa instrução não difere de duas instruções SSE2 executadas em duas metades do registro (pelo que entendi, os primeiros processadores com suporte ao AVX2 decodificaram cada instrução em duas ou mais microoperações, portanto o ganho de desempenho foi limitado pela fase de extração de instruções). Por exemplo,
_mm_dp_ps executa um produto escalar entre dois registros SSE2 e
_mm256_dp_ps produz dois produtos escalares entre duas metades de dois registros AVX2, portanto, é limitado a 4 por cada metade.
Por esse motivo, o código AVX2 geralmente difere do universal “SIM-8-wide SIM”, mas aqui funciona a nosso favor: em vez de tentar melhorar a vetorização através da transposição de vetores de 4-largura, retornamos à primeira versão do SIMD e dobramos o loop usando as instruções AVX2 em vez do SSE2 / SSE4. Ainda precisamos carregar e armazenar vetores de quatro largos, mas, em geral,
__m128 para
__m256 e
_mm_ para
_mm256 no
_mm256 com várias configurações:
unsigned int i00 = indices[(i + 0) * 3 + 0]; unsigned int i01 = indices[(i + 0) * 3 + 1]; unsigned int i02 = indices[(i + 0) * 3 + 2]; unsigned int i10 = indices[(i + 1) * 3 + 0]; unsigned int i11 = indices[(i + 1) * 3 + 1]; unsigned int i12 = indices[(i + 1) * 3 + 2]; __m256 p0 = _mm256_loadu2_m128( &vertex_positions[i10].x, &vertex_positions[i00].x); __m256 p1 = _mm256_loadu2_m128( &vertex_positions[i11].x, &vertex_positions[i01].x); __m256 p2 = _mm256_loadu2_m128( &vertex_positions[i12].x, &vertex_positions[i02].x); __m256 p10 = _mm256_sub_ps(p1, p0); __m256 p20 = _mm256_sub_ps(p2, p0); __m256 normal = _mm256_sub_ps( _mm256_mul_ps( _mm256_shuffle_ps(p10, p10, yzx), _mm256_shuffle_ps(p20, p20, zxy)), _mm256_mul_ps( _mm256_shuffle_ps(p10, p10, zxy), _mm256_shuffle_ps(p20, p20, yzx))); __m256 areasq = _mm256_dp_ps(normal, normal, dp_xyz); __m256 area = _mm256_sqrt_ps(areasq); __m256 areanz = _mm256_cmp_ps(area, _mm256_setzero_ps(), _CMP_NEQ_OQ); normal = _mm256_and_ps(_mm256_div_ps(normal, area), areanz); __m256 distance = _mm256_dp_ps(normal, p0, dp_xyz); __m256 negdistance = _mm256_sub_ps(_mm256_setzero_ps(), distance); __m256 normalnegdist = _mm256_blend_ps(normal, negdistance, 0x88); __m256 Qx = _mm256_mul_ps(normal, normal); __m256 Qy = _mm256_mul_ps( _mm256_shuffle_ps(normal, normal, _MM_SHUFFLE(3, 2, 2, 1)), _mm256_shuffle_ps(normal, normal, _MM_SHUFFLE(3, 0, 1, 0))); __m256 Qz = _mm256_mul_ps(negdistance, normalnegdist);
Aqui você pode pegar cada metade de 128 bits dos
Qz Qx /
Qz /
Qz recebidos e executar o mesmo código que usamos para adicionar os quadráticos. Em vez disso, assumimos que, se o triângulo tiver três vértices em uma célula (
single_cell == true ), é muito provável que o outro triângulo tenha três vértices em outra célula e executemos a agregação final dos quadráticos também usando o AVX2:
unsigned int c00 = vertex_cells[i00]; unsigned int c01 = vertex_cells[i01]; unsigned int c02 = vertex_cells[i02]; unsigned int c10 = vertex_cells[i10]; unsigned int c11 = vertex_cells[i11]; unsigned int c12 = vertex_cells[i12]; bool single_cell = (c00 == c01) & (c00 == c02) & (c10 == c11) & (c10 == c12); if (single_cell) { area = _mm256_mul_ps(area, _mm256_set1_ps(3.f)); Qx = _mm256_mul_ps(Qx, area); Qy = _mm256_mul_ps(Qy, area); Qz = _mm256_mul_ps(Qz, area); Quadric& q00 = cell_quadrics[c00]; Quadric& q10 = cell_quadrics[c10]; __m256 q0x = _mm256_loadu2_m128(&q10.a00, &q00.a00); __m256 q0y = _mm256_loadu2_m128(&q10.a10, &q00.a10); __m256 q0z = _mm256_loadu2_m128(&q10.b0, &q00.b0); _mm256_storeu2_m128(&q10.a00, &q00.a00, _mm256_add_ps(q0x, Qx)); _mm256_storeu2_m128(&q10.a10, &q00.a10, _mm256_add_ps(q0y, Qy)); _mm256_storeu2_m128(&q10.b0, &q00.b0, _mm256_add_ps(q0z, Qz)); } else {
O código resultante é mais simples, conciso e mais rápido que nossa abordagem sem êxito do SSE2:

Obviamente, não alcançamos uma aceleração de 8 vezes, mas apenas 2,45 vezes. As operações de carregamento e armazenamento ainda são de quatro dimensões, pois somos forçados a trabalhar com um layout de memória desconfortável devido à indexação dinâmica, e os cálculos não são ideais para o SIMD. Mas agora o
fillCellQuadrics não
fillCellQuadrics mais o gargalo em nosso pipeline de perfis e você pode se concentrar em outras funções.
Se reúnem, crianças
Economizamos 4,8 segundos na execução do teste (48 ms em cada execução) e agora nosso principal invasor é
countTriangles . Parece ser uma função simples, mas é executada não uma vez, mas cinco vezes:
static size_t countTriangles(const unsigned int* vertex_ids, const unsigned int* indices, size_t index_count) { size_t result = 0; for (size_t i = 0; i < index_count; i += 3) { unsigned int id0 = vertex_ids[indices[i + 0]]; unsigned int id1 = vertex_ids[indices[i + 1]]; unsigned int id2 = vertex_ids[indices[i + 2]]; result += (id0 != id1) & (id0 != id2) & (id1 != id2); } return result; }
A função enumera todos os triângulos de origem e calcula o número de triângulos não degenerados comparando os identificadores dos vértices. Não está claro imediatamente como paralelizar usando o SIMD ... a menos que você use as instruções de coleta.
O conjunto de instruções AVX2 adicionou a família de instruções de coleta / dispersão ao x64 SIMD; cada um deles usa um registro vetorial com 4 ou 8 valores - e simultaneamente executa 4 ou 8 operações de carregamento ou salvamento. Se você usar o reunir aqui, poderá fazer o download de três índices, executar o reunir todos de uma vez (ou em grupos de 4 ou 8) e comparar os resultados. Reunir-se nos processadores Intel tem sido historicamente muito lento, mas vamos tentar. Por uma questão de simplicidade, fazemos upload de dados para 8 triângulos, transpomos vetores de maneira semelhante à nossa tentativa anterior e comparamos os elementos correspondentes de cada vetor:
for (size_t i = 0; i < (triangle_count & ~7); i += 8) { __m256 tri0 = _mm256_loadu2_m128( (const float*)&indices[(i + 4) * 3 + 0], (const float*)&indices[(i + 0) * 3 + 0]); __m256 tri1 = _mm256_loadu2_m128( (const float*)&indices[(i + 5) * 3 + 0], (const float*)&indices[(i + 1) * 3 + 0]); __m256 tri2 = _mm256_loadu2_m128( (const float*)&indices[(i + 6) * 3 + 0], (const float*)&indices[(i + 2) * 3 + 0]); __m256 tri3 = _mm256_loadu2_m128( (const float*)&indices[(i + 7) * 3 + 0], (const float*)&indices[(i + 3) * 3 + 0]); _MM_TRANSPOSE8_LANE4_PS(tri0, tri1, tri2, tri3); __m256i i0 = _mm256_castps_si256(tri0); __m256i i1 = _mm256_castps_si256(tri1); __m256i i2 = _mm256_castps_si256(tri2); __m256i id0 = _mm256_i32gather_epi32((int*)vertex_ids, i0, 4); __m256i id1 = _mm256_i32gather_epi32((int*)vertex_ids, i1, 4); __m256i id2 = _mm256_i32gather_epi32((int*)vertex_ids, i2, 4); __m256i deg = _mm256_or_si256( _mm256_cmpeq_epi32(id1, id2), _mm256_or_si256( _mm256_cmpeq_epi32(id0, id1), _mm256_cmpeq_epi32(id0, id2))); result += 8 - _mm_popcnt_u32(_mm256_movemask_epi8(deg)) / 4; }
A macro
_MM_TRANSPOSE8_LANE4_PS no AVX2 é equivalente a
_MM_TRANSPOSE4_PS , que não é encontrada no cabeçalho padrão, mas é facilmente exibida. Ele pega quatro vetores AVX2 e transpõe duas matrizes 4 × 4 independentemente uma da outra:
#define _MM_TRANSPOSE8_LANE4_PS(row0, row1, row2, row3) \ do { \ __m256 __t0, __t1, __t2, __t3; \ __t0 = _mm256_unpacklo_ps(row0, row1); \ __t1 = _mm256_unpackhi_ps(row0, row1); \ __t2 = _mm256_unpacklo_ps(row2, row3); \ __t3 = _mm256_unpackhi_ps(row2, row3); \ row0 = _mm256_shuffle_ps(__t0, __t2, _MM_SHUFFLE(1, 0, 1, 0)); \ row1 = _mm256_shuffle_ps(__t0, __t2, _MM_SHUFFLE(3, 2, 3, 2)); \ row2 = _mm256_shuffle_ps(__t1, __t3, _MM_SHUFFLE(1, 0, 1, 0)); \ row3 = _mm256_shuffle_ps(__t1, __t3, _MM_SHUFFLE(3, 2, 3, 2)); \ } while (0)
Devido a alguns recursos dos conjuntos de instruções SSE2 / AVX2, devemos usar operações de registro de ponto flutuante ao transpor vetores. Estamos carregando os dados um pouco descuidadamente; mas basicamente não importa, porque o desempenho da coleta nos limita:

Agora o
countTriangles é cerca de 27% mais rápido e percebe o terrível CPI (ciclos por instrução): enviamos cerca de quatro vezes menos instruções, mas a coleta leva muito tempo. É ótimo que acelere o trabalho geral, mas, é claro, o ganho de desempenho é um pouco deprimente. Conseguimos ultrapassar
fillCellQuadrics no perfil, o que nos leva à última função no topo da lista, que ainda não analisamos.
Capítulo 6, onde tudo começa a funcionar como deveria
A última função é
computeVertexIds . No algoritmo, é realizado 6 vezes, portanto, também representa uma excelente meta para otimização. Pela primeira vez, vemos uma função que parece ter sido criada para uma otimização clara no SIMD:
static void computeVertexIds(unsigned int* vertex_ids, const Vector3* vertex_positions, size_t vertex_count, int grid_size) { assert(grid_size >= 1 && grid_size <= 1024); float cell_scale = float(grid_size - 1); for (size_t i = 0; i < vertex_count; ++i) { const Vector3& v = vertex_positions[i]; int xi = int(vx * cell_scale + 0.5f); int yi = int(vy * cell_scale + 0.5f); int zi = int(vz * cell_scale + 0.5f); vertex_ids[i] = (xi << 20) | (yi << 10) | zi; } }
Após as otimizações anteriores, sabemos o que fazer: desenrolar o ciclo 4 ou 8 vezes, pois não há sentido em tentar acelerar apenas uma iteração, transpor os componentes do vetor e executar os cálculos em paralelo. Vamos fazer isso com o AVX2, processando 8 vértices por vez:
__m256 scale = _mm256_set1_ps(cell_scale); __m256 half = _mm256_set1_ps(0.5f); for (size_t i = 0; i < (vertex_count & ~7); i += 8) { __m256 vx = _mm256_loadu2_m128( &vertex_positions[i + 4].x, &vertex_positions[i + 0].x); __m256 vy = _mm256_loadu2_m128( &vertex_positions[i + 5].x, &vertex_positions[i + 1].x); __m256 vz = _mm256_loadu2_m128( &vertex_positions[i + 6].x, &vertex_positions[i + 2].x); __m256 vw = _mm256_loadu2_m128( &vertex_positions[i + 7].x, &vertex_positions[i + 3].x); _MM_TRANSPOSE8_LANE4_PS(vx, vy, vz, vw); __m256i xi = _mm256_cvttps_epi32( _mm256_add_ps(_mm256_mul_ps(vx, scale), half)); __m256i yi = _mm256_cvttps_epi32( _mm256_add_ps(_mm256_mul_ps(vy, scale), half)); __m256i zi = _mm256_cvttps_epi32( _mm256_add_ps(_mm256_mul_ps(vz, scale), half)); __m256i id = _mm256_or_si256( zi, _mm256_or_si256( _mm256_slli_epi32(xi, 20), _mm256_slli_epi32(yi, 10))); _mm256_storeu_si256((__m256i*)&vertex_ids[i], id); }
E veja os resultados: aceleramos
aceleramos computeVertexIdsduas vezes. Considerando todas as otimizações, o tempo total de execução do programa foi reduzido para aproximadamente 120 ms, o que corresponde ao cálculo de 50 milhões de triângulos por segundo.Pode parecer que não atingimos novamente o aumento esperado de produtividade: computeVertexIdsnão deveria acelerar mais do que duas vezes após a paralelização? Para responder a essa pergunta, vamos tentar ver quanto trabalho essa função executa.computeVertexIdsé executado seis vezes para um início do programa: cinco vezes durante a pesquisa binária e uma vez no final para calcular os identificadores finais que são usados para processamento adicional. Cada vez, essa função processa 3 milhões de vértices, lendo 12 bytes para cada vértice e escrevendo 4 bytes.No total, mais de 100 execuções do inovador, essa função processa 1,8 bilhão de vértices, lendo 21 GB e retornando 7 GB. O processamento de 28 GB em 1,46 segundos requer uma largura de banda de barramento de 19 GB / s. Podemos verificar a largura de banda da memória executando memcmp(block1, block2, 512 MB). O resultado é 45 ms, ou seja, cerca de 22 GB / s em um núcleo (embora o benchmark AIDA64 mostre velocidades de leitura no meu sistema de até 31 GB / s, mas use vários núcleos). De fato, chegamos perto do limite máximo de memória alcançável e um aumento adicional no desempenho exigirá um empacotamento mais próximo desses vértices, para que ocupem menos de 12 bytes.Conclusão
Adotamos um algoritmo bastante otimizado que simplifica grades muito grandes a uma velocidade de 28 milhões de triângulos por segundo e usamos os conjuntos de instruções SSE e AVX para acelerar quase duas vezes, para 50 milhões de triângulos por segundo. Durante essa jornada, tivemos que aprender diferentes maneiras de usar o SIMD: registros para armazenar vetores de 3 largos, transposição de SoA, instruções AVX2 para armazenar dois vetores de 3 largos, reunir instruções para acelerar o carregamento de dados em comparação com instruções escalares e, finalmente, aplicamos diretamente o AVX2 para processamento de streaming.O SIMD geralmente não é o melhor ponto de partida para otimização: o racionalizador de malha passou por muitas iterações de otimização algorítmica e microoptimização sem usar instruções específicas da plataforma. Mas, em algum momento, essas possibilidades estão esgotadas e, se o desempenho for crítico, o SIMD é uma ferramenta fantástica que pode ser usada, se necessário.Não tenho certeza de qual dessas otimizações cairá no ramo principal meshoptimizer: no final, isso é apenas um experimento para ver como o código está com overclock sem alterar drasticamente os algoritmos. Espero que o artigo tenha sido informativo e tenha idéias para otimizar o código. As fontes finais deste artigo estão aqui ; este trabalho é baseado na versão do meshoptimizer 99ab49, e o modelo do Buda tailandês é publicado no Sketchfab .