1. Introdução
Vários artigos [1,2,3] foram publicados no Habr que direta ou indiretamente se relacionam com este tópico. Nesse sentido, não se pode deixar de observar a publicação [1] com o título “Matemática nos dedos: regulador linear-quadrático”, que popularmente explica o princípio de operação do controlador LQR ideal.
Eu queria continuar esse tópico, tendo examinado a aplicação prática do método de otimização dinâmica, mas já em um exemplo concreto usando Python. Primeiro, algumas palavras sobre a terminologia e o método de otimização dinâmica.
Os métodos de otimização são divididos em estático e dinâmico. O objeto de controle está em um estado de movimento contínuo sob a influência de vários fatores externos e internos. Portanto, a avaliação do resultado do controle é fornecida para o tempo de controle T, e essa é a tarefa da otimização dinâmica.
Usando métodos de otimização dinâmica, são resolvidos os problemas associados à distribuição de recursos limitados por um período de tempo, e a função objetivo é escrita como uma funcionalidade integral.
O aparato matemático para resolver tais problemas são métodos variacionais: cálculo clássico de variações, o princípio do L.S. máximo Pontryagin e programação dinâmica R. Bellman.
A análise e síntese dos sistemas de controle são realizadas nos espaços de tempo, frequência e estado. A análise e síntese de sistemas de controle no espaço de estados é introduzida no currículo, no entanto, as técnicas apresentadas nos materiais de treinamento usando o controlador SQR foram projetadas para o Matlab e não contêm exemplos práticos de análise.
O objetivo desta publicação é considerar os métodos de análise e síntese de sistemas de controle linear no espaço de estados usando o conhecido exemplo de otimização do sistema de controle de um acionamento elétrico e de uma aeronave usando a linguagem de programação Python.
Fundamentação matemática do método de otimização dinâmica
Para otimização, são utilizados os critérios de amplitude (MO), simétrica (CO) e ótimos de compromisso (KO).
Ao resolver problemas de otimização no espaço de estados, um sistema estacionário linear é dado por equações de matriz vetorial:
pontox= fracdxdt=A cdotx+B cdotu;y=C cdotx, (1)
Os critérios integrais para o consumo mínimo de energia de controle e a velocidade máxima são definidos pelos funcionais:
Jx= int infty0(xTQx+uTRu+2xTNu)dt rightarrowmin, 2)
Ju= int infty0(yTQy+uTRu+2yTNu)dt rightarrowmin. (3)
A lei de controle u está na forma de feedback linear nas variáveis de estado x ou nas variáveis de saída y:
u= pmKx,u= pmKyEsse controle minimiza os critérios de qualidade quadráticos (2), (3). Nas relações (1) ÷ (3), Q e R são matrizes definidas positivas simétricas de dimensão [n × n] e [m × m], respectivamente; K é uma matriz de coeficientes constantes de dimensão [m × n], cujos valores não são limitados. Se o parâmetro de entrada N for omitido, será considerado zero.
A solução para esse problema, que é chamado de problema de otimização quadrática integral linear (otimização LQR), no espaço de estados é determinada pela expressão:
u=R−1BTPxonde a matriz P deve satisfazer a equação de Ricatti:
ATP+PA+PBR−1BTP+Q=0Os critérios (2), (3) também são contraditórios, pois a implementação do primeiro termo requer uma fonte de potência infinitamente alta e, para o segundo, uma fonte de potência infinitamente baixa. Isso pode ser explicado pela seguinte expressão:
Jx= int infty0xTQxdt ,
qual é a norma
Mod(x) vetor x, isto é uma medida de sua oscilação no processo de regulação e, portanto, assume valores menores em transientes rápidos com menos oscilação e a expressão:
Ju= int infty0uTRudté uma medida da quantidade de energia usada para controle, é uma penalidade pelos custos de energia do sistema.
As matrizes de ponderação Q, R e N dependem das restrições das coordenadas correspondentes. Se qualquer elemento dessas matrizes for igual a zero, a coordenada correspondente não terá restrições. Na prática, a escolha dos valores das matrizes Q, R, N é realizada pelo método de estimativas de especialistas, tentativa, erro e depende da experiência e do conhecimento do engenheiro de projeto.
Para resolver esses problemas, foram utilizados os seguintes operadores do MATLAB:
beginbmatrixR,S,E endbmatrix=lqr(A,B,Q,R,N) e
beginbmatrixR,S,E endbmatrix=lqry(Ps,Q,R,N) que minimizam os funcionais (2), (3) pelo vetor de estado x ou pelo vetor de saída y.
Modelo de Objetos de Gerenciamento
Ps=ss(A,B,C,D). O resultado do cálculo é a matriz K de feedbacks ótimos em relação às variáveis de estado x, a solução da equação de Ricatti S e os valores próprios E = eiq (A-BK) do sistema de controle em malha fechada.
Componentes funcionais:
Jx=x0TP1x0,Ju=x0TP2x0onde x0 é o vetor de condições iniciais;
P1 e
P2 - matrizes desconhecidas que são uma solução das equações da matriz de Lyapunov. Eles são encontrados usando funções;
P1=lyap(NN,Q) e
P2=lyap(NN,KTRK) ,
NN=(A+BK)TRecursos da implementação do método de otimização dinâmica usando Python
Embora a Biblioteca de Sistemas de Controle Python [4] tenha funções: control.lqr, control.lyap, o uso de control.lqr é possível apenas se o módulo slycot estiver instalado, o que é um problema [5]. Ao usar a função lyap no contexto de uma tarefa, a otimização resulta em um control.exception.ControlArgument: Q deve ser um erro de matriz simétrica [6].
Portanto, para implementar as funções lqr () e lyap (), usei o scipy.linalg:
from numpy import* from scipy.linalg import* def lqr(A,B,Q,R): S =matrix(solve_continuous_are(A, B, Q, R)) K = matrix(inv(R)*(BT*S)) E= eig(AB*K)[0] return K, S, E P1=solve_lyapunov(NN,Ct*Q*C)
A propósito, você não deve abandonar completamente o controle, pois as funções step (), pole (), ss (), tf (), feedback (), acker (), place () e outras funcionam bem.
Um exemplo de otimização de LQR em um inversor elétrico
(um exemplo é retirado da publicação [7])Considere a síntese de um controlador quadrático-linear que satisfaça o critério (2) para um objeto de controle definido no espaço de estados por matrizes:
A = \ begin {bmatrix} & -100 & 0 & 0 \\ & 143.678 & -16.667 & -195.402 \\ & 0 & 1.046 & 0 \ end {bmatrix}; B = \ begin {bmatrix} 2300 \\ 0 \\ 0 \\ end {bmatrix}; C = \ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix}; D = 0
A = \ begin {bmatrix} & -100 & 0 & 0 \\ & 143.678 & -16.667 & -195.402 \\ & 0 & 1.046 & 0 \ end {bmatrix}; B = \ begin {bmatrix} 2300 \\ 0 \\ 0 \\ end {bmatrix}; C = \ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix}; D = 0
Os seguintes itens são considerados como variáveis de estado:
x1 - tensão do conversor, V;
x2 - corrente do motor, A;
x3 - velocidade angular
c−1 . Este é o sistema TP - DPT com HB: motor R nom = 30 kW; Unom = 220 V; Inom = 147 A ;;
omegaω 0 = 169
c−1 ;
omegaω max = 187
c−1 ; momento nominal de resistência Mnom = 150 N * m; multiplicidade da corrente de partida = 2; conversor de tiristores: Unom = 230 V; Uy = 10 B; Inom = 300 A; multiplicidade de sobrecorrente de curto prazo = 1,2.
Ao resolver o problema, aceitamos a matriz Q na diagonal. Como resultado da modelagem, verificou-se que os valores mínimos dos elementos da matriz R = 84 e
Q=[[0,01,0,0],[0,0,01,0],[0,0,0,01]]. Nesse caso, é observado um processo de transição monotônica da velocidade angular do motor (fig. 1). Em R = 840
Q=[[0,01,0,0],[0,0,01,0],[0,0,0,01]] processo transitório (Fig. 2) atende ao critério de MO. O cálculo das matrizes P1 e P2 foi realizado em x0 = [220 147 162].
Listando o programa (Fig. 1). 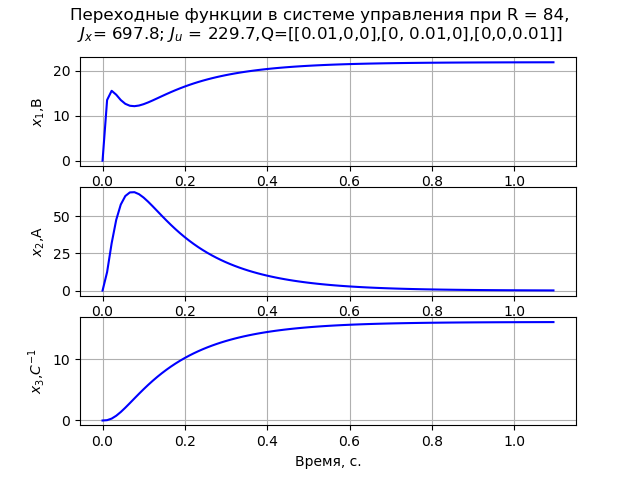 Fig. 1
Fig. 1Listando o programa (Fig. 2). 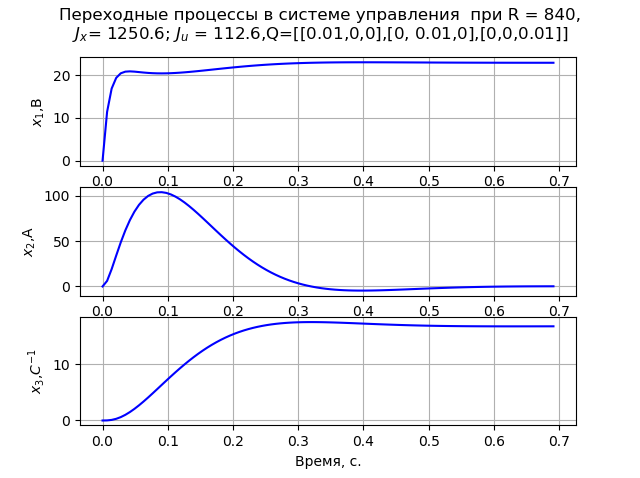 Fig. 2
Fig. 2Pela seleção apropriada das matrizes R e Q, é possível reduzir a corrente de partida do motor para valores aceitáveis iguais a (2–2,5) In (Fig. 3). Por exemplo, com R = 840 e
Q = ([[[0,01,0,0]], [0,0,88,0], [0,0,0,01]], seu valor é 292 A e o tempo de processo de transição sob essas condições é 1,57 s.
Listando o programa (Fig. 3). 
Fig.3
Em todos os casos considerados, os feedbacks sobre tensão e corrente são negativos e na velocidade, positivos, o que é indesejável de acordo com os requisitos de estabilidade. Além disso, o sistema sintetizado é astático para a tarefa e estático para a carga. Portanto, consideramos a síntese de um controlador PI no espaço de estados com uma variável de estado adicional
x4 - coeficiente de transferência do integrador.
Representamos as informações iniciais na forma de matrizes:
A = \ begin {bmatrix} & -100 & 0 & 0 & 0 \\ & 143.678 & -16.667 & -195.402 & 0 \\ & 0 & 1.046 & 0 & 0 \ 0 & 0 & 0 & 1 & 0 \ end {bmatrix}; B = \ begin {bmatrix} 2300 \\ 0 \\ 0 \\ 0 \\\ end {bmatrix}; C = olho (4)); D = 0Os transitórios de tarefas correspondentes ao critério MO foram obtidos em R = 100, q11 = q22 = q33 = 0,001 e q44 = 200. A Figura 4 mostra os transitórios das variáveis de estado confirmando o astatismo do sistema por tarefa e por carga.
Listagem de programas (Fig. 4). 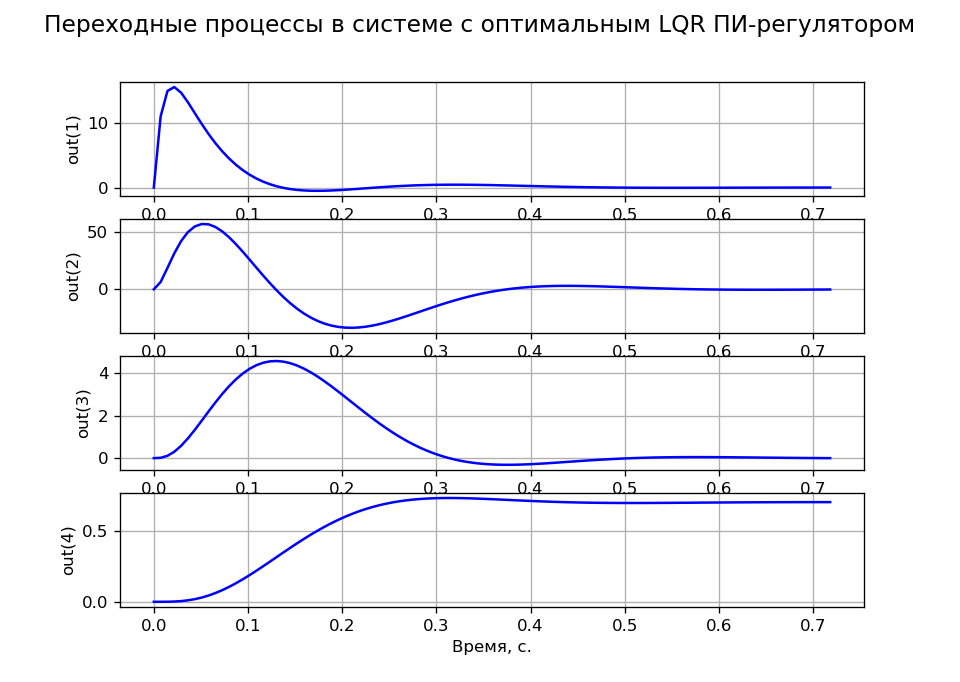 Fig. 4
Fig. 4Para determinar a matriz K, a Biblioteca de Sistemas de Controle Python possui duas funções K = acker (A, B, s) e K = place (A, B, s), onde s é o vetor - a linha dos polos desejados da função de transferência do sistema de controle de circuito fechado. O primeiro comando pode ser usado apenas para sistemas com uma entrada em u para n≤5. O segundo não possui essas restrições, mas a multiplicidade dos polos não deve exceder a classificação da matriz B. Um exemplo do uso do operador acker () é mostrado na listagem e na (Fig. 5).
Listagem de programas (Fig. 5).  Fig. 5
Fig. 5Conclusão
A implementação da otimização do drive LQR apresentada na publicação, levando em consideração o uso das novas funções lqr () e lyap (), permitirá abandonar o uso do programa MATLAB licenciado ao estudar a seção correspondente da teoria de controle.
Um exemplo de otimização de LQR em uma aeronave (LA)
(um exemplo é retirado da publicação de Astrom e Mruray, capítulo 5 [8] e finalizado pelo autor do artigo em termos de substituição da função lqr () e redução da terminologia para a geralmente aceita)A parte teórica, uma breve teoria, a otimização do LQR já foi considerada acima, então vamos para a análise de código com os comentários correspondentes:
Bibliotecas necessárias e função do controlador LQR. from scipy.linalg import*
Condições iniciais e matrizes básicas modelos A, B, C, D. xe = [0, 0, 0, 0, 0, 0];
Construímos entradas e saídas correspondentes a alterações passo a passo na posição xy. Os vetores xd e yd correspondem ao estado estacionário desejado no sistema. Matrizes Cx e Cy são as saídas correspondentes do modelo. Para descrever a dinâmica do sistema, usamos um sistema de equações da matriz vetorial:
\ left \ {\ begin {matrix} xdot = Ax + Bu => xdot = (A-BK) x + xd \\ u = -K (x-xd) \\ y = Cx \\ \ end {matriz} \ right.
A dinâmica de um loop fechado pode ser modelada usando a função step (), para K \ cdot xd e K \ cdot xd como vetores de entrada, onde:
xd = matrix([[1], [0], [0], [0], [0], [0]]); yd = matrix([[0], [1], [0], [0], [0], [0]]);
A biblioteca de controle atual 0.8.1 suporta apenas parte das funções do SISO Matlab para criar controladores de feedback; portanto, para ler dados do controlador, é necessário criar vetores de índice lat (), alt () para a dinâmica lateral -x e vertical -y.
lat = (0,2,3,5); alt = (1,4);
Os gráficos são exibidos sequencialmente, um para cada tarefa.
figure(); title(" x y") plot(Tx.T, Yx.T, '-', Ty.T, Yy.T, '--'); plot([0, 10], [1, 1], 'k-'); axis([0, 10, -0.1, 1.4]); ylabel(' '); xlabel(''); legend(('x', 'y'), loc='lower right'); grid() show()
Gráfico: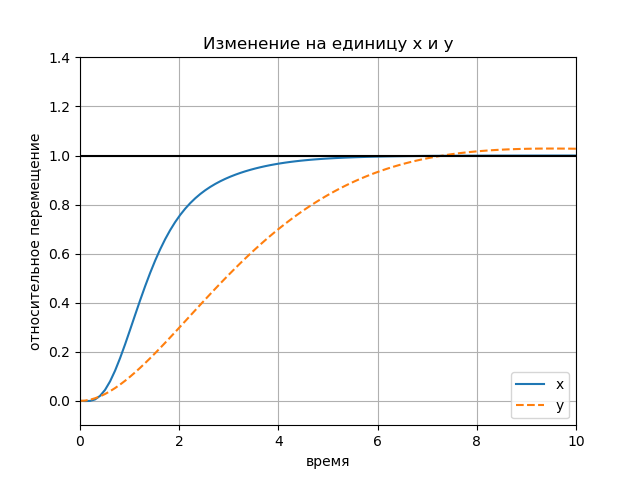
A influência da amplitude das ações de entrada Gráfico: Gráfico:
Gráfico: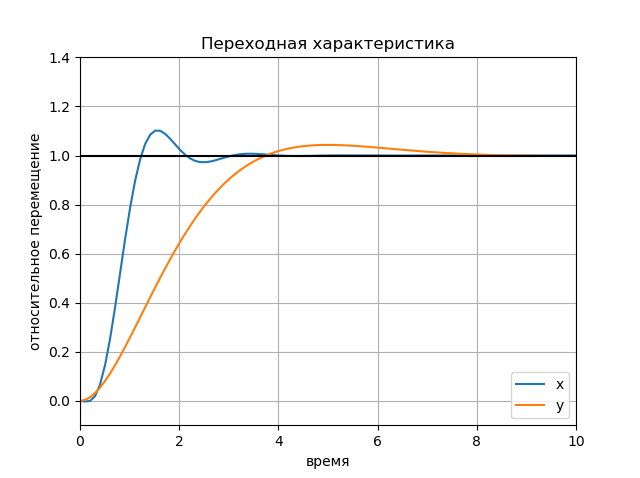
Resposta transitória fisicamente baseada Gráfico: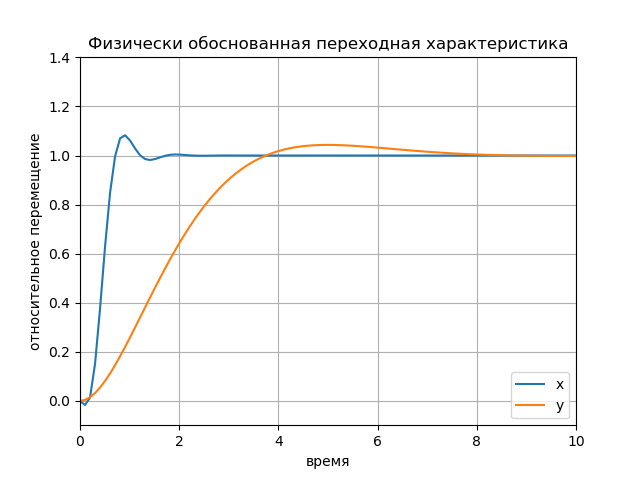
Conclusão:
A implementação da otimização do LQR na aeronave apresentada na publicação, levando em consideração o uso da nova função lqr (), permite abandonar o uso do programa licenciado MATLAB ao estudar a seção correspondente da teoria de controle.
Referências
1.
Matemática nos dedos: controlador linear-quadrático.2.
O espaço de estados nos problemas de projetar sistemas de controle ideais.3.
Usando a Biblioteca de Sistemas de Controle Python para projetar sistemas de controle automático.4.
Biblioteca de sistemas de controle Python.5.
Python - não é possível importar o módulo slycot para o spyder (RuntimeError & ImportError).6.
Biblioteca de sistemas de controle Python.7.
Critérios para controle ideal e otimização do lqr em um inversor elétrico.