Como um quebra-cabeça infantil ajuda a revelar os segredos do magnetismo

Os ímãs são familiares às pessoas desde os tempos antigos, mas a física do ferromagnetismo permanece um mistério. Agora, um quebra-cabeça familiar aproxima os físicos de responder perguntas

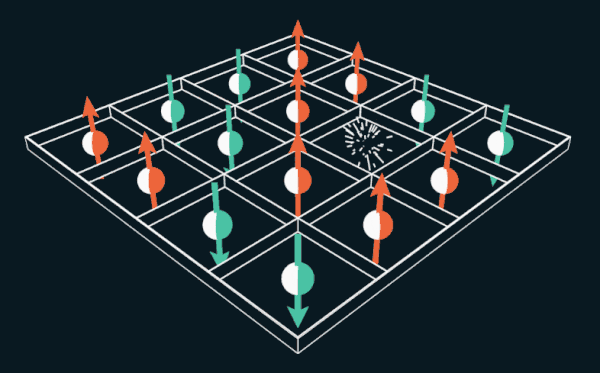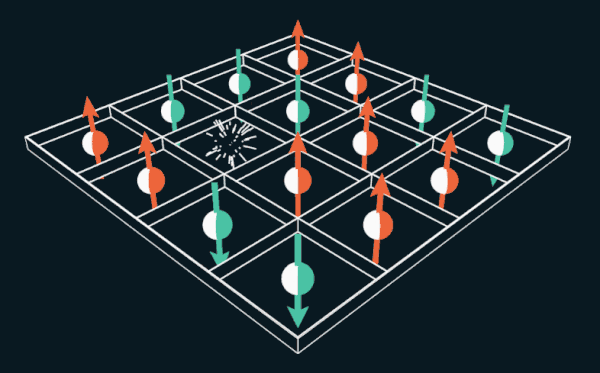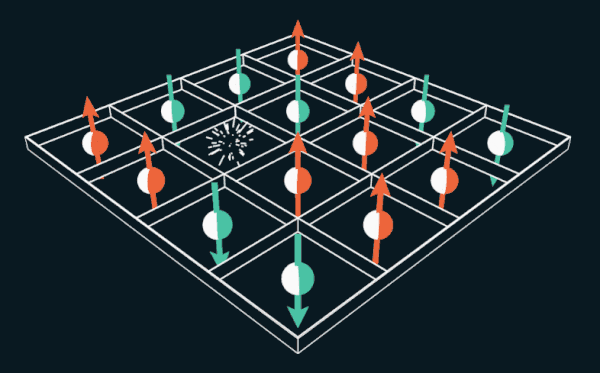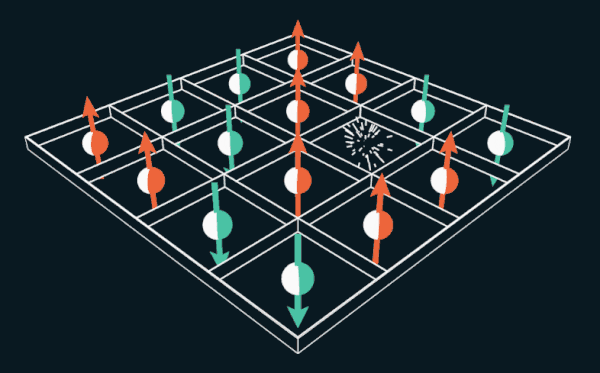O jogo de 15 oferece ao jogador para mover as peças numeradas dentro da grade. Se você substituir os números pelos giros dos elétrons, o quebra-cabeça pode ser usado para explicar como os ímãs permanentes funcionam.

Por vários meses no ano de 1880, regiões inteiras dos Estados Unidos sucumbiram ao vício, análogos dos quais ninguém havia visto anteriormente. "Uma epidemia literalmente eclodiu em todo o país", escreveu a revista The Weekly News-Democrat em Imperia, Kansas, em 12 de março de 1880. "Cidades inteiras são atraídas, as pessoas perdem o sono e ficam loucas". A epidemia se espalhou pela Europa e chegou à Austrália com a Nova Zelândia.

A doença tornou-se uma nova paixão: desencorajar o simples quebra-cabeça mecânico "15". Ainda é conhecido e consiste em um campo quadrado 4x4 no qual você pode mover 15 peças numeradas para organizá-las.

Pelos padrões de hoje, o jogo parece antiquado, mas em 1880 estava no auge da popularidade. "Nenhuma criança pode resistir a esse entretenimento, nenhum adulto será tão forte ou arrogante para escapar de seu charme", escreveu o jornal. E a decepção pode ter decorrido do fato matematicamente comprovado de que apenas metade das configurações deste quebra-cabeça pode ser resolvida com sucesso (o que provavelmente era desconhecido para aqueles que sofreram sua influência).

Hoje, quase 140 anos depois, o interesse pelo jogo "15" ressurgiu novamente, mas desta vez não funciona como uma distração, mas como uma maneira de entender um quebra-cabeça aparentemente não relacionado e muito mais complicado: como os ímãs funcionam.

Ímãs permanentes, como os que ficam pendurados na porta da geladeira, são atraídos por um fenômeno como o ferromagnetismo . Em um ferro-ímã, os spins dos elétrons são alinhados e juntos geram um campo magnético. Mais precisamente, metais como ferro, cobalto e níquel exibem magnetismo de banda, pois seus elétrons são capazes de se mover livremente dentro do material. Cada elétron tem seu próprio momento magnético, mas, para entender como e por que todos esses momentos se alinham em um ímã, é necessário calcular as interações quânticas entre todos os elétrons, o que é excessivamente difícil.

"O magnetismo de zona é realmente um dos maiores desafios da física teórica da matéria condensada", disse Wai Lee, físico da Universidade Johns Hopkins.

No entanto, Lee e dois estudantes de graduação, Eric Bobrov e Keaton Stewbis, podem ter chegado um pouco mais perto de resolver esse problema. Usando o quebra-cabeça matemático "15", eles expandiram o teorema conhecido que descreve o estado idealizado do magnetismo da zona. Em sua nova análise , publicada na Physical Review B, eles estendem o teorema para explicar um sistema mais amplo e realista, o que poderia levar a um modelo mais preciso de ímãs.

"É um ótimo trabalho", disse Daniel Arovas , físico da Universidade da Califórnia, em San Diego. "Gosto especialmente deste trabalho devido ao fato de haver poucos resultados detalhados sobre o magnetismo de zona e eles serem muito fragmentados."

Buraco pulando

No nível mais básico, os elétrons em um metal devem obedecer a duas restrições principais. Em primeiro lugar, todos são carregados negativamente, portanto se repelem. Em segundo lugar, os elétrons são obrigados a obedecer aos chamados o princípio de Pauli, que postula que duas partículas [com um giro meio inteiro / aprox. trans.] não pode estar no mesmo estado quântico. Isso significa que elétrons com o mesmo spin - proporcional ao momento magnético de um elétron - não podem ocupar o mesmo estado em um átomo de metal. E dois elétrons com giros opostos podem.

Acontece que a maneira mais simples de satisfazer tanto a repulsão mútua quanto as limitações do princípio de Pauli para um grupo de elétrons será separar e alinhar os spins - como resultado do qual o material se torna ferromagnético.

No entanto, esta é apenas uma imagem simplificada. Os físicos não conseguiram construir um modelo detalhado da aparência de um padrão tão organizado de rotações alinhadas a partir de inúmeras interações quânticas entre elétrons individuais. Por exemplo, como Lee explicou, a função de onda de um elétron - uma descrição matemática complexa de suas propriedades quânticas - pode ser confundida com a função de onda de outro elétron. Para entender completamente como o comportamento de partículas individuais leva ao aparecimento de um fenômeno coletivo como o ferromagnetismo, você precisará monitorar a função de onda de cada elétron no sistema, enquanto ele altera continuamente a função de onda de cada um dos elétrons restantes no processo de interação. Na prática, esse emaranhado generalizado torna impossível escrever as equações completas e abrangentes necessárias para descrever o ferromagnetismo.

Em vez disso, os físicos, incluindo Lee, estão tentando coletar informações estudando modelos simplificados e idealizados que descrevem a física por trás do ferromagnetismo. Em particular, seu último trabalho estende uma importante descoberta feita há mais de 50 anos.

Em meados da década de 1960, dois físicos de lados opostos do globo obtiveram evidências independentes que provam por que os elétrons devem se alinhar e criar um estado ferromagnético. David Tules, então físico que trabalhou na Universidade de Cambridge e acabou ganhando o Prêmio Nobel de 2016, e Yosuke Nagaoka, físico da Universidade de Nagoya que estava visitando a Universidade de San Diego na época, publicou suas evidências em 1965 e 1966, respectivamente. . Seu resultado, chamado teorema de Nagaoki-Tules (ou simplesmente o teorema de Nagaoki), baseia-se em um sistema idealizado de elétrons localizado em uma rede atômica. Portanto, embora não explique o comportamento de ímãs reais, ainda era importante, mostrando pela primeira vez em princípio por que os spins de elétrons deveriam estar alinhados. E como a análise deles era evidência matemática, eles eram precisos, não sobrecarregados com aproximações típicas da física.

Para entender o teorema, imagine uma rede quadrada bidimensional. Cada nó pode colocar dois elétrons com giros opostos, mas o teorema sugere que colocar dois elétrons em um único local exigirá uma quantidade infinita de energia. Isso garante que apenas um elétron esteja em cada lugar. Nesta configuração, cada elétron pode direcionar sua rotação para cima ou para baixo. Eles não precisam se alinhar, portanto esse sistema não deve ser um ferro-ímã.


Wai Lee, físico da Universidade Johns Hopkins

Agora nós removemos um elétron. Como resultado, haverá um local vago chamado de buraco. Um elétron vizinho pode deslizar para dentro de um buraco, deixando para trás um novo espaço vazio. Outro elétron pode se mover para um novo local vazio, deixando outro buraco para trás. Neste exemplo, um buraco, de fato, salta de um lugar para outro, movendo-se ao redor da grade. Thules e Nagaoka descobriram que, neste caso, quando um único orifício é adicionado, os elétrons se alinham espontaneamente. Eles provaram que seria o estado com menos energia, o estado de um ferro-ímã.

Arovas explica que, para que um sistema entre em um estado com a menor energia, um buraco deve poder se mover livremente sem perturbar a configuração dos spins de elétrons - esse processo exigirá energia adicional. Mas quando um buraco se move, os elétrons também devem se mover. Para que os elétrons se movam sem perturbar a configuração dos spins, eles devem estar alinhados.

"O teorema de Nagaoka é um dos poucos exemplos que podem provar matematicamente casos individuais de ferromagnetismo", disse Masaki Oshikawa , físico da Universidade de Tóquio. "Mas, do ponto de vista da física, tudo isso é muito artificial."

Por exemplo, os elétrons requerem muita energia para superar sua repulsa mútua e se estabelecerem em um só lugar - mas não infinitos, como exige o teorema. Além disso, a figura desenhada por Nagaoka e Tules se aplica apenas a redes simples: redes bidimensionais que consistem em quadrados ou triângulos ou redes tridimensionais cúbicas. Na natureza, o ferromagnetismo surge em muitos metais com estruturas de todo tipo.

Se o teorema de Nagaoka-Tules realmente explica o ferromagnetismo, ele deve ser aplicável a todas as redes. As pessoas supunham que sim, disse Lee. "Mas ninguém deu evidências reais e claras." Bem, isto é, ainda.

Azulejos com encosto

Em 1989, Hal Tasaki, físico da Universidade Gakushuin do Japão, estendeu esse teorema para descobrir que ele seria aplicável desde que a estrutura tivesse uma propriedade matemática como conectividade. Tome o caso simples de uma treliça quadrada com um furo em movimento. Se, ao mover um furo, você puder reproduzir qualquer configuração de rotações, mantendo o número de elétrons, com rotações direcionadas para cima e para baixo, a condição de conexão será satisfeita.

Mas, além de redes quadradas e triangulares e cubos tridimensionais, não estava claro se a condição conectada seria satisfeita em outros casos - e, portanto, quão amplamente esse teorema poderia ser aplicado.

Para lidar com esse problema, Lee começou com uma grade hexagonal em favo de mel. Seus alunos, Bobrov e Stubis, trabalhando nessa tarefa, perceberam que ela se assemelha a uma mania do século XIX: o quebra-cabeça "15". Troque as etiquetas dos números dos números para as costas, para cima e para baixo, e o quebra-cabeça se torna equivalente ao ferro-ímã Nagaoki, com um buraco se movendo ao longo da rede de elétrons.

O quebra-cabeça é permitido quando você tem a oportunidade de redistribuir os blocos em qualquer sequência, que coincida totalmente com a condição de conectividade. Portanto, a questão de saber se a condição de conexão é satisfeita para uma dada rede torna-se a questão de se é possível resolver um quebra-cabeça equivalente em uma rede de tal estrutura.

Acontece que em 1974 o matemático Richard Wilson, agora trabalhando no Instituto de Tecnologia da Califórnia, resolveu esse problema resumindo e resolvendo o quebra-cabeça "15" para todas as grades. Como parte da prova, ele mostrou que em quase todas as redes inseparáveis ​​(nas quais todos os nós permanecem conectados mesmo após a remoção de uma delas), é possível mover os blocos e obter qualquer configuração, enquanto o número de movimentos permanece uniforme. A única exceção é que polígonos únicos são maiores que um triângulo e algo chamado “gráfico θnulo”, no qual o vértice no centro do hexágono é conectado a dois vértices opostos.

Os pesquisadores foram capazes de aplicar diretamente a prova de Wilson ao teorema de Nagaoka-Tules. Eles provaram que a condição de conectividade é satisfeita para um sistema de elétrons e um único furo em quase todas as redes, incluindo estruturas comuns como favos de mel bidimensionais e redes tridimensionais em forma de diamante. Duas exceções - polígonos maiores que um triângulo e o gráfico θnull - em qualquer caso, não ocorrem em ferromagnetos reais.

Explosão buraco

Usar o quebra-cabeça "15" é uma abordagem nova e potencialmente frutífera, disse Sriram Shastri , físico da Universidade da Califórnia em Santa Cruz. "Gosto do fato de ele ter trazido para o trabalho uma nova linguagem, um novo conjunto de conexões com a teoria dos grafos", disse ele. "Acho que essa é uma conexão rica - no futuro, pode se tornar uma rica fonte de idéias". Mas, embora a pesquisa esteja dando um passo significativo adiante, os problemas permanecem.

Uma complicação é que o teorema de Nagaoki-Tules nem sempre funciona quando um buraco em movimento precisa dar um número ímpar de passos enquanto se move ao longo da rede, disse Shastri. Talvez o problema mais impressionante seja que o teorema requer a presença de exatamente um buraco - nem mais nem menos. No entanto, os metais estão cheios de buracos; eles costumam ocupar até a metade da rede.

Mas os físicos tentaram generalizar o teorema de sistemas com muitos buracos. Usando métodos numéricos, os físicos mostraram que o ferromagnetismo de Nagaoki parece funcionar para uma treliça quadrada de tamanho finito, até 30% dos quais são buracos. No trabalho atual, os pesquisadores aplicaram técnicas analíticas precisas em favos de mel bidimensionais e em treliças tridimensionais em forma de diamante. Aparentemente, o ferromagnetismo de Nagaoki existe desde que o número de furos não exceda o número de nós da rede no grau 1/2 para as células e no grau 2/5 na rede em forma de diamante.

Essas soluções exatas podem levar a um modelo mais completo de magnetismo de zona. "Este é apenas um pequeno passo para estabelecer um ponto de partida matemático rigoroso para pesquisas futuras", disse Lee.