Alguns dias atrás eu tinha um
concurso online para o jogo .
1.199 pessoas participaram do concurso on-line e houve mais de 5.000 decisões, entre as quais 61 tentativas de contornar o sistema, identificando vulnerabilidades. Isso é muito legal, obrigado a todos que participaram.
Este jogo é um tipo de "
jogos do coronel Blotto ". Dois jogadores participam. Cada um tem o mesmo número de recursos que devem ser colocados no campo NxM. O vencedor é aquele que recebe mais células (ou seja, o número de seus recursos nele é maior que o do oponente). Esta é a condição para a nossa tarefa
Condição1. Dois estão jogando.
2. O campo de jogo é um tabuleiro 3 por 3.
3. Cada jogador tem um exército de 100 fuzileiros espaciais.
4. Antes da batalha noturna, cada lado secretamente coloca suas tropas de maneira aleatória em 9 células. Em cada célula, você pode colocar qualquer número inteiro de fuzileiros espaciais de 0 a 100.
5. De manhã, a batalha pelo próximo planeta começa. Em cada uma das 9 células, o jogador que tiver mais Astartes nessa célula vence. Para uma vitória em cada uma das 9 células, é dado 1 ponto. Se o mesmo número estiver em um determinado quadrado, a batalha nesse quadrado terminará empatada e os dois jogadores receberão 0,5 pontos.
6. A batalha é vencida por quem ganhou mais campos. Se ambos os jogadores venceram 4,5 campos, a batalha termina em empate.
Quando iniciei esse experimento, ainda não sabia que este jogo não tinha uma solução ideal, mas graças aos comentários pude entender melhor esse tópico.
Vamos começar com os vencedores deste jogo.
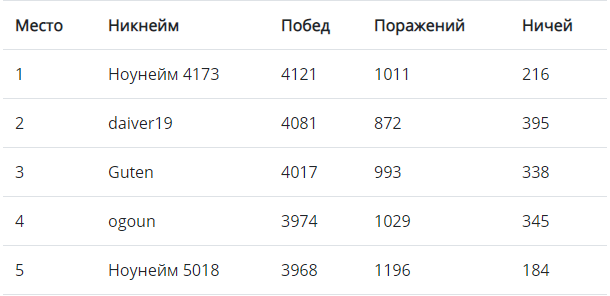
A melhor decisão marcou 4121 vitórias - um resultado muito bom. Mas o que aconteceria se apenas as soluções TOP-100 participassem do jogo?
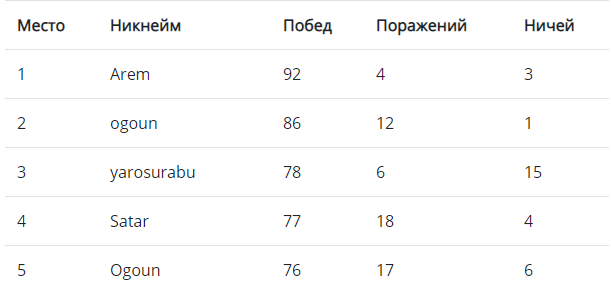
Surpreendentemente, ele nem chegou ao top5 (no 8º lugar), e o primeiro lugar foi tomado pela decisão do 68º lugar.
Isso apenas mostra que não há solução melhor. Outros resultados podem ser vistos em
game.pavlukhinlab.comMas o que mais você pode aprender?
Os jogadores colocam os maiores números no centro, em média, todos os jogadores preenchem a primeira linha com grandes números, enquanto os melhores resultados dão mais ênfase aos resultados finais.
valores médios para todos os jogos (à esquerda) e TOP-100 (à direita)Bem, e mais exemplos das melhores estratégias:
Exemplos de estratégias Ogoun (6 soluções no TOP-100) Exemplos de estratégias de Guten (8 soluções no TOP-100) As melhores estratégias selecionaram 5 células principais, as células restantes foram preenchidas com pequenos valores. O que é lógico, porque para vencer basta levar 5 células.
Bem, agora alguns gráficos.
Distribuição probabilística de números:
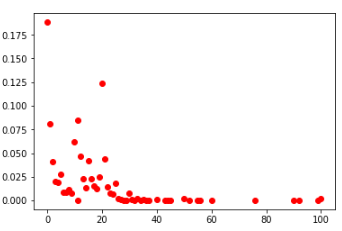
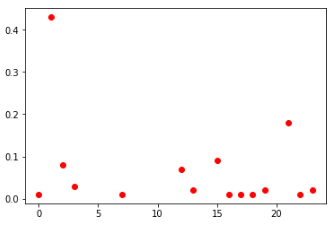segundas células entre todos os jogadores (esquerda) e TOP-100 (direita)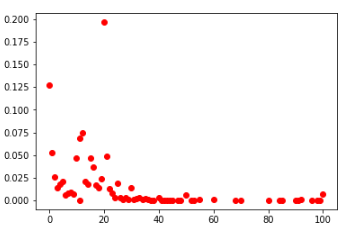
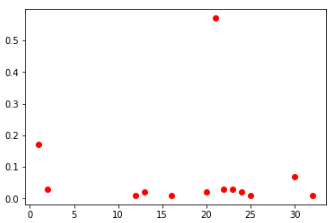células centrais entre todos e TOP-100
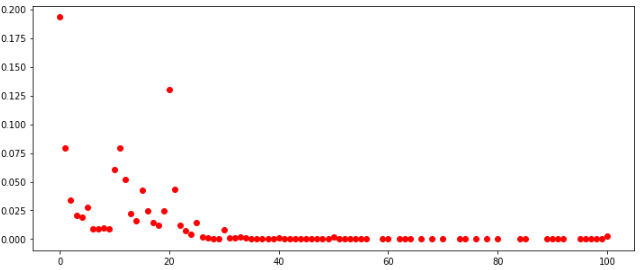distribuição de números em todos os jogos
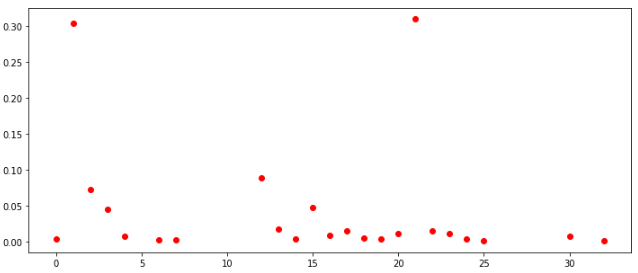distribuição de números de acordo com TOP-100Se você observar a distribuição em todas as células entre todos os jogadores, eles geralmente serão semelhantes. Pode-se concluir também que, nessas condições, não faz sentido preencher as células com valores maiores que 30.
É aqui que o estudo termina - é tudo o que consegui extrair desses dados. Talvez um de vocês possa oferecer outra coisa que possa verificar - estou esperando por você nos comentários. Procure jogos impessoais
aqui .
Py.Sy. Em um post anterior, eu falei sobre um neurônio que estava aprendendo a jogar esse jogo. Infelizmente, nada disso ainda foi alcançado. Dois neurônios decidiram que a melhor estratégia é jogar zeros na saída e aproveitar o sorteio. Mas talvez eu descubra novamente e faça um post separado sobre os erros que cometi ao criar um neurônio e, possivelmente, sucesso.