Equações diferenciais ordinárias neurais

Uma proporção significativa de processos é descrita por equações diferenciais; pode ser a evolução do sistema físico ao longo do tempo, a condição médica do paciente, características fundamentais do mercado de ações, etc. Os dados sobre esses processos são de natureza consistente e contínua, no sentido de que as observações são simplesmente manifestações de algum tipo de estado em constante mudança.

Há também outro tipo de dados seriais, são dados discretos, por exemplo, dados de tarefas da PNL. O estado desses dados varia discretamente: de um caractere ou palavra para outro.

Agora, ambos os tipos de dados seriais são geralmente processados por redes recursivas, embora sejam de natureza diferente e pareçam exigir abordagens diferentes.

Um artigo muito interessante foi apresentado na última conferência do NIPS , que pode ajudar a resolver esse problema. Os autores propõem uma abordagem que eles chamaram de EDOs Neurais .

Aqui, tentei reproduzir e resumir os resultados deste artigo para facilitar um pouco a familiarização com a ideia dela. Parece-me que essa nova arquitetura pode muito bem encontrar um lugar nas ferramentas padrão de um cientista de dados, além de redes convolucionais e recorrentes.

Figura 1: A retropropagação em gradiente contínuo requer a solução da equação diferencial aumentada no tempo.

As setas representam o ajuste dos gradientes propagados para trás pelos gradientes das observações.

Ilustração do artigo original.

Declaração do problema

Que haja um processo que obedeça a alguma ODE desconhecida e que haja várias observações (barulhentas) ao longo da trajetória do processo

$\ frac {dz} {dt} = f (z (t), t) \; (1)$

$\ {(z_0, t_0), (z_1, t_1), ..., (z_M, t_M) \} - \ text {apresentações}$

Como encontrar uma aproximação $\ widehat {f.} (z, t, \ teta)$ funções do alto-falante f (z, t)

?

Primeiro, considere uma tarefa mais simples: existem apenas duas observações, no início e no final da trajetória, (z_0, t_0), (z_1, t_1)

.

A evolução do sistema começa a partir do estado z_0, t_0

a tempo

com algumas funções dinâmicas parametrizadas usando qualquer método de evolução de sistemas ODE. Depois que o sistema estiver em um novo estado $\ hat {z_1}, t_1$ , é comparado com o estado z_1

e a diferença entre eles é minimizada variando os parâmetros $\ theta$ funções dinâmicas.

Ou, formalmente, considere minimizar a função de perda $L (\ hat {z_1})$ :

$L (z (t_1)) = L \ Big (\ int_ {t_0} ^ {t_1} f (z (t), t, \ theta) dt \ Big) = L \ big (\ text {ODESolve} (z ( t_0), f, t_0, t_1, \ theta) \ grande) \; 2)$

Para minimizar

, você precisa calcular os gradientes para todos os seus parâmetros: $z (t_0), t_0, t_1, \ theta$ . Para fazer isso, primeiro você precisa determinar como

depende do estado a cada momento no tempo (z (t))

$a (t) = - \ frac {\ L parcial} {\ parcial z (t)} \; (3)$

é chamado estado adjunto , sua dinâmica é dada por outra equação diferencial, que pode ser considerada um análogo contínuo da diferenciação de uma função complexa ( regra da cadeia ):

$\ frac {d a (t)} {d t} = -a (t) \ frac {\ f parcial (z (t), t, \ teta)} {\ z parcial} \; 4)$

O resultado desta fórmula pode ser encontrado no apêndice do artigo original.

Os vetores neste artigo devem ser considerados vetores em minúsculas, embora o artigo original use uma representação de linha e coluna.

Resolvendo o diffur (4) no tempo, obtemos uma dependência do estado inicial z (t_0)

$\ frac {\ L parcial} {\ parcial z (t_0)} = \ int_ {t_1} ^ {t_0} a (t) \ frac {\ parcial f (z (t), t, \ theta)} {\ parcial z} dt \; (5)$

Para calcular o gradiente em relação a

e $\ theta$ , você pode simplesmente considerá-los parte do estado. Essa condição é chamada de aumentada . A dinâmica desse estado é trivialmente obtida a partir da dinâmica original:

$\ frac {d} {dt} \ begin {bmatrix} z \\ \ theta \\ t \ end {bmatrix} (t) = f _ {\ text {aug}} ([z, \ theta, t]): = \ begin {bmatrix} f ([z, \ theta, t]) \\ 0 \\ 1 \ end {bmatrix} \; (6)$

Em seguida, o estado conjugado para esse estado aumentado:

$a _ {\ text {aug}}: = \ begin {bmatrix} a \\ a _ {\ theta} \\ a_t \ end {bmatrix}, a _ {\ theta} (t): = \ frac {\ L parcial} \ parcial \ teta (t)}, a_t (t): = \ frac {\ parcial L} {\ parcial t (t)} \; (7)$

Dinâmica aumentada de gradiente:

$\ frac {\ parcial f _ {\ text {aug}}} {\ parcial [z, \ theta, t]} = \ begin {bmatrix} \ frac {\ parcial f} {\ parcial z} &; \ frac {\ parcial f} {\ parcial \ theta} &; \ frac {\ parcial f} {\ parcial t} \\ 0 &; 0 &; 0 \\ 0 &; 0 &; 0 \ end {bmatrix} \; (8)$

A equação diferencial do estado aumentado conjugado da fórmula (4) então:

$\ frac {d a _ {\ text {aug}}} {dt} = - \ begin {bmatrix} a \ frac {\ parcial f} {\ parcial z} &; a \ frac {\ parcial f} {\ parcial \ theta} &; a \ frac {\ parcial f} {\ parcial t} \ end {bmatrix} \; (9)$

A solução desse ODE de volta no tempo produz:

$\ frac {\ L parcial} {\ parcial z (t_0)} = \ int_ {t_1} ^ {t_0} a (t) \ frac {\ parcial f (z (t), t, \ theta)} {\ parcial z} dt \; (10)$

$\ frac {\ L parcial} {\ parcial \ theta} = \ int_ {t_1} ^ {t_0} a (t) \ frac {\ parcial f (z (t), t, \ theta)} {\ parcial \ theta } dt \; 11)$

$\ frac {\ L parcial} {\ parcial t_0} = \ int_ {t_1} ^ {t_0} a (t) \ frac {\ parcial f (z (t), t, \ teta)} {\ parcial t} dt \; (12)$

O que há com

$\ frac {\ L parcial} {\ parcial t_1} = - a (t) \ frac {\ parcial f (z (t), t, \ teta)} {\ parcial t} \; (13)$

fornece gradientes em todos os parâmetros de entrada ao solucionador ODESolve ODE.

Todos os gradientes (10), (11), (12), (13) podem ser calculados juntos em uma chamada ODESolve com a dinâmica do estado aumentado conjugado (9).

Ilustração do artigo original.

O algoritmo acima descreve a propagação reversa do gradiente da solução ODE para observações sucessivas.

No caso de várias observações em uma trajetória, tudo é calculado da mesma maneira, mas, nos momentos das observações, o inverso do gradiente distribuído deve ser ajustado com gradientes da observação atual, como mostra a Figura 1 .

Implementação

O código abaixo é minha implementação de ODEs Neurais . Fiz isso puramente para uma melhor compreensão do que está acontecendo. No entanto, está muito próximo do que é implementado no repositório dos autores do artigo. Ele contém todo o código que você precisa entender em um só lugar; também é um pouco mais comentado. Para aplicações e experimentos reais, ainda é melhor usar a implementação dos autores do artigo original.

import math import numpy as np from IPython.display import clear_output from tqdm import tqdm_notebook as tqdm import matplotlib as mpl import matplotlib.pyplot as plt %matplotlib inline import seaborn as sns sns.color_palette("bright") import matplotlib as mpl import matplotlib.cm as cm import torch from torch import Tensor from torch import nn from torch.nn import functional as F from torch.autograd import Variable use_cuda = torch.cuda.is_available()

Primeiro, você precisa implementar qualquer método para a evolução dos sistemas ODE. Por uma questão de simplicidade, o método Euler é implementado aqui, embora qualquer método explícito ou implícito seja adequado.

 def ode_solve(z0, t0, t1, f): """     -   """ h_max = 0.05 n_steps = math.ceil((abs(t1 - t0)/h_max).max().item()) h = (t1 - t0)/n_steps t = t0 z = z0 for i_step in range(n_steps): z = z + h * f(z, t) t = t + h return z

Também descreve a superclasse de uma função dinâmica parametrizada com alguns métodos úteis.

Primeiro: você precisa retornar todos os parâmetros dos quais a função depende na forma de um vetor.

Segundo: é necessário calcular a dinâmica aumentada. Essa dinâmica depende do gradiente da função parametrizada em termos de parâmetros e dados de entrada. Para não precisar registrar o gradiente com cada ponteiro para cada nova arquitetura, usaremos o método torch.autograd.grad .

 class ODEF(nn.Module): def forward_with_grad(self, z, t, grad_outputs): """Compute f and a df/dz, a df/dp, a df/dt""" batch_size = z.shape[0] out = self.forward(z, t) a = grad_outputs adfdz, adfdt, *adfdp = torch.autograd.grad( (out,), (z, t) + tuple(self.parameters()), grad_outputs=(a), allow_unused=True, retain_graph=True ) #  grad       , #  expand   if adfdp is not None: adfdp = torch.cat([p_grad.flatten() for p_grad in adfdp]).unsqueeze(0) adfdp = adfdp.expand(batch_size, -1) / batch_size if adfdt is not None: adfdt = adfdt.expand(batch_size, 1) / batch_size return out, adfdz, adfdt, adfdp def flatten_parameters(self): p_shapes = [] flat_parameters = [] for p in self.parameters(): p_shapes.append(p.size()) flat_parameters.append(p.flatten()) return torch.cat(flat_parameters)

O código abaixo descreve a propagação para a frente e para trás dos ODEs Neurais . É necessário separar esse código do módulo torch.nn.Module na forma da função torch.autograd.Function porque nesse último você pode implementar um método arbitrário de retropropagação , em oposição a um módulo. Então isso é apenas uma muleta.

Esse recurso está subjacente a toda a abordagem da ODE Neural .

 class ODEAdjoint(torch.autograd.Function): @staticmethod def forward(ctx, z0, t, flat_parameters, func): assert isinstance(func, ODEF) bs, *z_shape = z0.size() time_len = t.size(0) with torch.no_grad(): z = torch.zeros(time_len, bs, *z_shape).to(z0) z[0] = z0 for i_t in range(time_len - 1): z0 = ode_solve(z0, t[i_t], t[i_t+1], func) z[i_t+1] = z0 ctx.func = func ctx.save_for_backward(t, z.clone(), flat_parameters) return z @staticmethod def backward(ctx, dLdz): """ dLdz shape: time_len, batch_size, *z_shape """ func = ctx.func t, z, flat_parameters = ctx.saved_tensors time_len, bs, *z_shape = z.size() n_dim = np.prod(z_shape) n_params = flat_parameters.size(0) #   , #       def augmented_dynamics(aug_z_i, t_i): """   -     t_i -   : bs, 1 aug_z_i -   : bs, n_dim*2 + n_params + 1 """ #     z_i, a = aug_z_i[:, :n_dim], aug_z_i[:, n_dim:2*n_dim] # Unflatten z and a z_i = z_i.view(bs, *z_shape) a = a.view(bs, *z_shape) with torch.set_grad_enabled(True): t_i = t_i.detach().requires_grad_(True) z_i = z_i.detach().requires_grad_(True) faug = func.forward_with_grad(z_i, t_i, grad_outputs=a) func_eval, adfdz, adfdt, adfdp = faug adfdz = adfdz if adfdz is not None else torch.zeros(bs, *z_shape) adfdp = adfdp if adfdp is not None else torch.zeros(bs, n_params) adfdt = adfdt if adfdt is not None else torch.zeros(bs, 1) adfdz = adfdz.to(z_i) adfdp = adfdp.to(z_i) adfdt = adfdt.to(z_i) # Flatten f and adfdz func_eval = func_eval.view(bs, n_dim) adfdz = adfdz.view(bs, n_dim) return torch.cat((func_eval, -adfdz, -adfdp, -adfdt), dim=1) dLdz = dLdz.view(time_len, bs, n_dim) # flatten dLdz   with torch.no_grad(): ##      #    , #       adj_z = torch.zeros(bs, n_dim).to(dLdz) adj_p = torch.zeros(bs, n_params).to(dLdz) #    z  p,        adj_t = torch.zeros(time_len, bs, 1).to(dLdz) for i_t in range(time_len-1, 0, -1): z_i = z[i_t] t_i = t[i_t] f_i = func(z_i, t_i).view(bs, n_dim) #      dLdz_i = dLdz[i_t] dLdt_i = torch.bmm(torch.transpose(dLdz_i.unsqueeze(-1), 1, 2), f_i.unsqueeze(-1))[:, 0] #     adj_z += dLdz_i adj_t[i_t] = adj_t[i_t] - dLdt_i #      aug_z = torch.cat(( z_i.view(bs, n_dim), adj_z, torch.zeros(bs, n_params).to(z) adj_t[i_t]), dim=-1 ) #  ()      aug_ans = ode_solve(aug_z, t_i, t[i_t-1], augmented_dynamics) #       adj_z[:] = aug_ans[:, n_dim:2*n_dim] adj_p[:] += aug_ans[:, 2*n_dim:2*n_dim + n_params] adj_t[i_t-1] = aug_ans[:, 2*n_dim + n_params:] del aug_z, aug_ans ##         #    dLdz_0 = dLdz[0] dLdt_0 = torch.bmm(torch.transpose(dLdz_0.unsqueeze(-1), 1, 2), f_i.unsqueeze(-1))[:, 0] #  adj_z += dLdz_0 adj_t[0] = adj_t[0] - dLdt_0 return adj_z.view(bs, *z_shape), adj_t, adj_p, None

Agora, por conveniência, envolva essa função no nn.Module .

 class NeuralODE(nn.Module): def __init__(self, func): super(NeuralODE, self).__init__() assert isinstance(func, ODEF) self.func = func def forward(self, z0, t=Tensor([0., 1.]), return_whole_sequence=False): t = t.to(z0) z = ODEAdjoint.apply(z0, t, self.func.flatten_parameters(), self.func) if return_whole_sequence: return z else: return z[-1]

Aplicação

Recuperação da função dinâmica real (verificação de abordagem)

Como teste básico, vamos agora verificar se o ODE Neural pode restaurar a verdadeira função da dinâmica usando dados observacionais.

Para isso, primeiro determinamos a função dinâmica do ODE, evoluímos a trajetória com base nele e tentamos restaurá-lo a partir da função dinâmica parametrizada aleatoriamente.

Primeiro, vamos verificar o caso mais simples de uma EDO linear. A função dinâmica é apenas a ação de uma matriz.

$\ frac {dz} {dt} = \ begin {bmatrix} -0,1 &; -1,0 \\ 1,0 &; -0,1 \ end {bmatrix} z$

A função treinada é parametrizada por uma matriz aleatória.

Além disso, uma dinâmica um pouco mais sofisticada (sem gif, porque o processo de aprendizado não é tão bonito :))
A função de aprendizado aqui é uma rede totalmente conectada com uma camada oculta.

Código

 class LinearODEF(ODEF): def __init__(self, W): super(LinearODEF, self).__init__() self.lin = nn.Linear(2, 2, bias=False) self.lin.weight = nn.Parameter(W) def forward(self, x, t): return self.lin(x)

A função dinâmica é apenas uma matriz

 class SpiralFunctionExample(LinearODEF): def __init__(self): matrix = Tensor([[-0.1, -1.], [1., -0.1]]) super(SpiralFunctionExample, self).__init__(matrix)

Matriz aleatoriamente parametrizada

 class RandomLinearODEF(LinearODEF): def __init__(self): super(RandomLinearODEF, self).__init__(torch.randn(2, 2)/2.)

Dinâmica para trajetórias mais sofisticadas

 class TestODEF(ODEF): def __init__(self, A, B, x0): super(TestODEF, self).__init__() self.A = nn.Linear(2, 2, bias=False) self.A.weight = nn.Parameter(A) self.B = nn.Linear(2, 2, bias=False) self.B.weight = nn.Parameter(B) self.x0 = nn.Parameter(x0) def forward(self, x, t): xTx0 = torch.sum(x*self.x0, dim=1) dxdt = torch.sigmoid(xTx0) * self.A(x - self.x0) + torch.sigmoid(-xTx0) * self.B(x + self.x0) return dxdt

Dinâmica de aprendizado na forma de uma rede totalmente conectada

 class NNODEF(ODEF): def __init__(self, in_dim, hid_dim, time_invariant=False): super(NNODEF, self).__init__() self.time_invariant = time_invariant if time_invariant: self.lin1 = nn.Linear(in_dim, hid_dim) else: self.lin1 = nn.Linear(in_dim+1, hid_dim) self.lin2 = nn.Linear(hid_dim, hid_dim) self.lin3 = nn.Linear(hid_dim, in_dim) self.elu = nn.ELU(inplace=True) def forward(self, x, t): if not self.time_invariant: x = torch.cat((x, t), dim=-1) h = self.elu(self.lin1(x)) h = self.elu(self.lin2(h)) out = self.lin3(h) return out def to_np(x): return x.detach().cpu().numpy() def plot_trajectories(obs=None, times=None, trajs=None, save=None, figsize=(16, 8)): plt.figure(figsize=figsize) if obs is not None: if times is None: times = [None] * len(obs) for o, t in zip(obs, times): o, t = to_np(o), to_np(t) for b_i in range(o.shape[1]): plt.scatter(o[:, b_i, 0], o[:, b_i, 1], c=t[:, b_i, 0], cmap=cm.plasma) if trajs is not None: for z in trajs: z = to_np(z) plt.plot(z[:, 0, 0], z[:, 0, 1], lw=1.5) if save is not None: plt.savefig(save) plt.show() def conduct_experiment(ode_true, ode_trained, n_steps, name, plot_freq=10): # Create data z0 = Variable(torch.Tensor([[0.6, 0.3]])) t_max = 6.29*5 n_points = 200 index_np = np.arange(0, n_points, 1, dtype=np.int) index_np = np.hstack([index_np[:, None]]) times_np = np.linspace(0, t_max, num=n_points) times_np = np.hstack([times_np[:, None]]) times = torch.from_numpy(times_np[:, :, None]).to(z0) obs = ode_true(z0, times, return_whole_sequence=True).detach() obs = obs + torch.randn_like(obs) * 0.01 # Get trajectory of random timespan min_delta_time = 1.0 max_delta_time = 5.0 max_points_num = 32 def create_batch(): t0 = np.random.uniform(0, t_max - max_delta_time) t1 = t0 + np.random.uniform(min_delta_time, max_delta_time) idx = sorted(np.random.permutation( index_np[(times_np > t0) & (times_np < t1)] )[:max_points_num]) obs_ = obs[idx] ts_ = times[idx] return obs_, ts_ # Train Neural ODE optimizer = torch.optim.Adam(ode_trained.parameters(), lr=0.01) for i in range(n_steps): obs_, ts_ = create_batch() z_ = ode_trained(obs_[0], ts_, return_whole_sequence=True) loss = F.mse_loss(z_, obs_.detach()) optimizer.zero_grad() loss.backward(retain_graph=True) optimizer.step() if i % plot_freq == 0: z_p = ode_trained(z0, times, return_whole_sequence=True) plot_trajectories(obs=[obs], times=[times], trajs=[z_p], save=f"assets/imgs/{name}/{i}.png") clear_output(wait=True) ode_true = NeuralODE(SpiralFunctionExample()) ode_trained = NeuralODE(RandomLinearODEF()) conduct_experiment(ode_true, ode_trained, 500, "linear") func = TestODEF(Tensor([[-0.1, -0.5], [0.5, -0.1]]), Tensor([[0.2, 1.], [-1, 0.2]]), Tensor([[-1., 0.]])) ode_true = NeuralODE(func) func = NNODEF(2, 16, time_invariant=True) ode_trained = NeuralODE(func) conduct_experiment(ode_true, ode_trained, 3000, "comp", plot_freq=30)

Como você pode ver, o Neural ODE faz um bom trabalho ao restaurar a dinâmica. Ou seja, o conceito como um todo funciona.
Agora verifique um problema um pouco mais complicado (MNIST, haha).

ODE neural inspirado em ResNets

No ResNet'ax, o estado latente muda de acordo com a fórmula

$h_ {t + 1} = h_ {t} + f (h_ {t}, \ theta_ {t})$

onde $t \ in \ {0 ... T \}$ O número do bloco e

esta é uma função aprendida pelas camadas dentro do bloco.

No limite, se dermos um número infinito de blocos com etapas cada vez menores, obteremos a dinâmica contínua da camada oculta na forma de uma ODE, exatamente como o que estava acima.

$\ frac {dh (t)} {dt} = f (h (t), t, \ teta)$

A partir da camada de entrada h (0)

podemos definir a camada de saída h (T)

como uma solução para este ODE no tempo T.

Agora podemos contar $\ theta$ como parâmetros distribuídos ( compartilhados ) entre todos os blocos infinitesimais.

Validando a arquitetura Neural ODE no MNIST

Nesta parte, testaremos a capacidade do ODE Neural de ser usado como componentes em arquiteturas mais familiares.

Em particular, substituiremos os blocos residuais pelo ODE Neural no classificador MNIST.

Código

 def norm(dim): return nn.BatchNorm2d(dim) def conv3x3(in_feats, out_feats, stride=1): return nn.Conv2d(in_feats, out_feats, kernel_size=3, stride=stride, padding=1, bias=False) def add_time(in_tensor, t): bs, c, w, h = in_tensor.shape return torch.cat((in_tensor, t.expand(bs, 1, w, h)), dim=1) class ConvODEF(ODEF): def __init__(self, dim): super(ConvODEF, self).__init__() self.conv1 = conv3x3(dim + 1, dim) self.norm1 = norm(dim) self.conv2 = conv3x3(dim + 1, dim) self.norm2 = norm(dim) def forward(self, x, t): xt = add_time(x, t) h = self.norm1(torch.relu(self.conv1(xt))) ht = add_time(h, t) dxdt = self.norm2(torch.relu(self.conv2(ht))) return dxdt class ContinuousNeuralMNISTClassifier(nn.Module): def __init__(self, ode): super(ContinuousNeuralMNISTClassifier, self).__init__() self.downsampling = nn.Sequential( nn.Conv2d(1, 64, 3, 1), norm(64), nn.ReLU(inplace=True), nn.Conv2d(64, 64, 4, 2, 1), norm(64), nn.ReLU(inplace=True), nn.Conv2d(64, 64, 4, 2, 1), ) self.feature = ode self.norm = norm(64) self.avg_pool = nn.AdaptiveAvgPool2d((1, 1)) self.fc = nn.Linear(64, 10) def forward(self, x): x = self.downsampling(x) x = self.feature(x) x = self.norm(x) x = self.avg_pool(x) shape = torch.prod(torch.tensor(x.shape[1:])).item() x = x.view(-1, shape) out = self.fc(x) return out func = ConvODEF(64) ode = NeuralODE(func) model = ContinuousNeuralMNISTClassifier(ode) if use_cuda: model = model.cuda() import torchvision img_std = 0.3081 img_mean = 0.1307 batch_size = 32 train_loader = torch.utils.data.DataLoader( torchvision.datasets.MNIST("data/mnist", train=True, download=True, transform=torchvision.transforms.Compose([ torchvision.transforms.ToTensor(), torchvision.transforms.Normalize((img_mean,), (img_std,)) ]) ), batch_size=batch_size, shuffle=True ) test_loader = torch.utils.data.DataLoader( torchvision.datasets.MNIST("data/mnist", train=False, download=True, transform=torchvision.transforms.Compose([ torchvision.transforms.ToTensor(), torchvision.transforms.Normalize((img_mean,), (img_std,)) ]) ), batch_size=128, shuffle=True ) optimizer = torch.optim.Adam(model.parameters()) def train(epoch): num_items = 0 train_losses = [] model.train() criterion = nn.CrossEntropyLoss() print(f"Training Epoch {epoch}...") for batch_idx, (data, target) in tqdm(enumerate(train_loader), total=len(train_loader)): if use_cuda: data = data.cuda() target = target.cuda() optimizer.zero_grad() output = model(data) loss = criterion(output, target) loss.backward() optimizer.step() train_losses += [loss.item()] num_items += data.shape[0] print('Train loss: {:.5f}'.format(np.mean(train_losses))) return train_losses def test(): accuracy = 0.0 num_items = 0 model.eval() criterion = nn.CrossEntropyLoss() print(f"Testing...") with torch.no_grad(): for batch_idx, (data, target) in tqdm(enumerate(test_loader), total=len(test_loader)): if use_cuda: data = data.cuda() target = target.cuda() output = model(data) accuracy += torch.sum(torch.argmax(output, dim=1) == target).item() num_items += data.shape[0] accuracy = accuracy * 100 / num_items print("Test Accuracy: {:.3f}%".format(accuracy)) n_epochs = 5 test() train_losses = [] for epoch in range(1, n_epochs + 1): train_losses += train(epoch) test() import pandas as pd plt.figure(figsize=(9, 5)) history = pd.DataFrame({"loss": train_losses}) history["cum_data"] = history.index * batch_size history["smooth_loss"] = history.loss.ewm(halflife=10).mean() history.plot(x="cum_data", y="smooth_loss", figsize=(12, 5), title="train error")

 Testing... 100% 79/79 [00:01<00:00, 45.69it/s] Test Accuracy: 9.740% Training Epoch 1... 100% 1875/1875 [01:15<00:00, 24.69it/s] Train loss: 0.20137 Testing... 100% 79/79 [00:01<00:00, 46.64it/s] Test Accuracy: 98.680% Training Epoch 2... 100% 1875/1875 [01:17<00:00, 24.32it/s] Train loss: 0.05059 Testing... 100% 79/79 [00:01<00:00, 46.11it/s] Test Accuracy: 97.760% Training Epoch 3... 100% 1875/1875 [01:16<00:00, 24.63it/s] Train loss: 0.03808 Testing... 100% 79/79 [00:01<00:00, 45.65it/s] Test Accuracy: 99.000% Training Epoch 4... 100% 1875/1875 [01:17<00:00, 24.28it/s] Train loss: 0.02894 Testing... 100% 79/79 [00:01<00:00, 45.42it/s] Test Accuracy: 99.130% Training Epoch 5... 100% 1875/1875 [01:16<00:00, 24.67it/s] Train loss: 0.02424 Testing... 100% 79/79 [00:01<00:00, 45.89it/s] Test Accuracy: 99.170%

Após um treinamento muito duro durante apenas 5 eras e 6 minutos de treinamento, o modelo já atingiu um erro de teste inferior a 1%. Podemos dizer que as EDOs Neurais se integram bem como um componente em redes mais tradicionais.

Em seu artigo, os autores também comparam esse classificador (ODE-Net) com uma rede regular totalmente conectada, com o ResNet com arquitetura semelhante e com exatamente a mesma arquitetura, na qual o gradiente se propaga diretamente por meio de operações no ODESolve (sem o método do gradiente conjugado) ( RK-Net).

Ilustração do artigo original.

Segundo eles, uma rede totalmente conectada em uma camada com aproximadamente o mesmo número de parâmetros que o Neural ODE tem um erro muito maior no teste, o ResNet com o mesmo erro tem muito mais parâmetros e o RK-Net sem o método de gradiente conjugado apresenta um erro um pouco maior e com o aumento linear do consumo de memória (quanto menor o erro permitido, mais etapas o ODESolve deve executar , o que aumenta linearmente o consumo de memória com o número de etapas).

Os autores usam o método implícito de Runge-Kutta com tamanho de etapa adaptável em sua implementação, diferentemente do método mais simples de Euler aqui. Eles também estudam algumas propriedades da nova arquitetura.

Recurso ODE-Net (NFE Forward - o número de cálculos de funções em um passe direto)
Ilustração do artigo original.

(a) Alterar o nível aceitável de erro numérico altera o número de etapas na distribuição direta.
(b) O tempo gasto na distribuição direta é proporcional ao número de cálculos de funções.
(c) O número de cálculos da função na propagação reversa é aproximadamente metade da propagação direta, o que indica que o método do gradiente conjugado pode ser mais computacionalmente eficiente do que a propagação do gradiente diretamente através do ODESolve .
(d) À medida que a ODE-Net se torna cada vez mais treinada, exige cada vez mais cálculos de uma função (uma etapa cada vez menor), possivelmente adaptando-se à crescente complexidade do modelo.

Função Generativa Oculta para Modelagem de Séries Temporais

O ODE neural é adequado para processar dados seriais contínuos, mesmo quando o caminho está em um espaço oculto desconhecido.

Nesta seção, experimentaremos e mudaremos a geração de seqüências contínuas usando o Neural ODE e daremos uma olhada no espaço oculto aprendido.

Os autores também comparam isso com seqüências semelhantes geradas por redes recorrentes.

O experimento aqui é um pouco diferente do exemplo correspondente no repositório dos autores; aqui há um conjunto mais diversificado de caminhos.

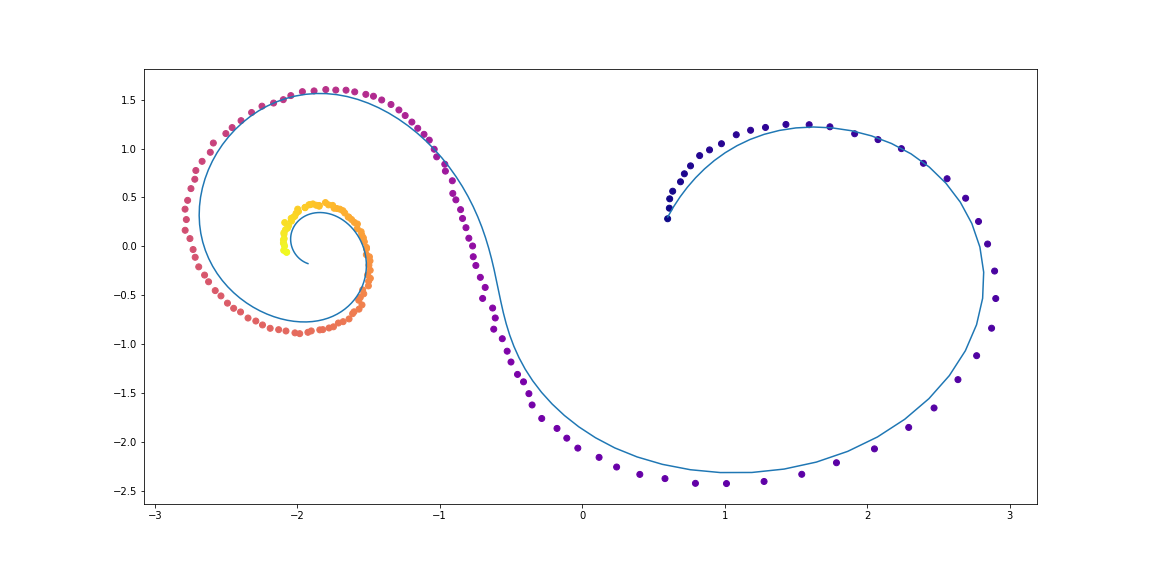
Dados

Os dados do treinamento consistem em espirais aleatórias, metade das quais no sentido horário e a segunda no sentido anti-horário. Além disso, subsequências aleatórias são amostradas dessas espirais, processadas pelo modelo de recorrência de codificação na direção oposta, dando origem a um estado oculto inicial, que depois evolui, criando uma trajetória no espaço oculto. Esse caminho latente é então mapeado para o espaço de dados e comparado com a subsequência amostrada. Assim, o modelo aprende a gerar trajetórias semelhantes a um conjunto de dados.

Exemplos de espirais de conjunto de dados

VAE como modelo generativo

Modelo generativo através de um procedimento de amostragem:

$z_ {t_0} \ sim \ mathcal {N} (0, I)$

$z_ {t_1}, z_ {t_2}, ..., z_ {t_M} = \ text {ODESolve} (z_ {t_0}, f, \ theta_f, t_0, ..., t_M)$

$x_ {t_i} \ sim p (x \ médio z_ {t_i}; \ theta_x)$

Que pode ser treinado usando a abordagem variada de codificador automático.

Passe por um codificador recorrente por uma sequência de tempo no tempo para obter os parâmetros $\ mu_ {z_ {t_0}}$ , $\ sigma_ {z_ {t_0}}$ distribuição posterior variacional e depois faça uma amostra:

$z_ {t_0} \ sim q \ left (z_ {t_0} \ mid x_ {t_0}, ..., x_ {t_M}; t_0, ..., t_M; \ theta_q \ right) = \ mathcal {N} \ esquerda (z_ {t_0} \ mid \ mu_ {z_ {t_0}} \ sigma_ {z_ {t_0}} \ direita)$

Obtenha trajetória oculta:

$z_ {t_1}, z_ {t_2}, ..., z_ {t_N} = \ text {ODESolve} (z_ {t_0}, f, \ theta_f, t_0, ..., t_N), \ text {where} \ frac {dz} {dt} = f (z, t; \ theta_f)$

Mapeie um caminho oculto para um caminho nos dados usando outra rede neural: $\ hat {x_ {t_i}} (z_ {t_i}, t_i; \ theta_x)$
Maximize a avaliação do limite inferior de validade (ELBO) para o caminho amostrado:

$\ text {ELBO} \ approx N \ Big (\ sum_ {i = 0} ^ {M} \ log p (x_ {t_i} \ meio z_ {t_i} (z_ {t_0}; \ theta_f); \ theta_x) + KL \ left (q (z_ {t_0} \ mid x_ {t_0}, ..., x_ {t_M}; t_0, ..., t_M; \ theta_q) \ paralela \ mathcal {N} (0, I) \ à direita) \ Big)$

E no caso de uma distribuição posterior gaussiana $p (x \ mid z_ {t_i}; \ theta_x)$ e nível de ruído conhecido $\ sigma_x$ :

$\ text {ELBO} \ approx -N \ Big (\ sum_ {i = 1} ^ {M} \ frac {(x_i - \ hat {x_i}) ^ 2} {\ sigma_x ^ 2} - \ log \ sigma_ { z_ {t_0}} ^ 2 + \ mu_ {z_ {t_0}} ^ 2 + \ sigma_ {z_ {t_0}} ^ 2 \ Big) + C$

O gráfico de computação de um modelo ODE oculto pode ser representado da seguinte maneira

Ilustração do artigo original.

Esse modelo pode ser testado para saber como ele interpola o caminho usando apenas as observações iniciais.

Código

Definir modelos

 class RNNEncoder(nn.Module): def __init__(self, input_dim, hidden_dim, latent_dim): super(RNNEncoder, self).__init__() self.input_dim = input_dim self.hidden_dim = hidden_dim self.latent_dim = latent_dim self.rnn = nn.GRU(input_dim+1, hidden_dim) self.hid2lat = nn.Linear(hidden_dim, 2*latent_dim) def forward(self, x, t): # Concatenate time to input t = t.clone() t[1:] = t[:-1] - t[1:] t[0] = 0. xt = torch.cat((x, t), dim=-1) _, h0 = self.rnn(xt.flip((0,))) # Reversed # Compute latent dimension z0 = self.hid2lat(h0[0]) z0_mean = z0[:, :self.latent_dim] z0_log_var = z0[:, self.latent_dim:] return z0_mean, z0_log_var class NeuralODEDecoder(nn.Module): def __init__(self, output_dim, hidden_dim, latent_dim): super(NeuralODEDecoder, self).__init__() self.output_dim = output_dim self.hidden_dim = hidden_dim self.latent_dim = latent_dim func = NNODEF(latent_dim, hidden_dim, time_invariant=True) self.ode = NeuralODE(func) self.l2h = nn.Linear(latent_dim, hidden_dim) self.h2o = nn.Linear(hidden_dim, output_dim) def forward(self, z0, t): zs = self.ode(z0, t, return_whole_sequence=True) hs = self.l2h(zs) xs = self.h2o(hs) return xs class ODEVAE(nn.Module): def __init__(self, output_dim, hidden_dim, latent_dim): super(ODEVAE, self).__init__() self.output_dim = output_dim self.hidden_dim = hidden_dim self.latent_dim = latent_dim self.encoder = RNNEncoder(output_dim, hidden_dim, latent_dim) self.decoder = NeuralODEDecoder(output_dim, hidden_dim, latent_dim) def forward(self, x, t, MAP=False): z_mean, z_log_var = self.encoder(x, t) if MAP: z = z_mean else: z = z_mean + torch.randn_like(z_mean) * torch.exp(0.5 * z_log_var) x_p = self.decoder(z, t) return x_p, z, z_mean, z_log_var def generate_with_seed(self, seed_x, t): seed_t_len = seed_x.shape[0] z_mean, z_log_var = self.encoder(seed_x, t[:seed_t_len]) x_p = self.decoder(z_mean, t) return x_p

Geração de conjunto de dados

 t_max = 6.29*5 n_points = 200 noise_std = 0.02 num_spirals = 1000 index_np = np.arange(0, n_points, 1, dtype=np.int) index_np = np.hstack([index_np[:, None]]) times_np = np.linspace(0, t_max, num=n_points) times_np = np.hstack([times_np[:, None]] * num_spirals) times = torch.from_numpy(times_np[:, :, None]).to(torch.float32) # Generate random spirals parameters normal01 = torch.distributions.Normal(0, 1.0) x0 = Variable(normal01.sample((num_spirals, 2))) * 2.0 W11 = -0.1 * normal01.sample((num_spirals,)).abs() - 0.05 W22 = -0.1 * normal01.sample((num_spirals,)).abs() - 0.05 W21 = -1.0 * normal01.sample((num_spirals,)).abs() W12 = 1.0 * normal01.sample((num_spirals,)).abs() xs_list = [] for i in range(num_spirals): if i % 2 == 1: # Make it counter-clockwise W21, W12 = W12, W21 func = LinearODEF(Tensor([[W11[i], W12[i]], [W21[i], W22[i]]])) ode = NeuralODE(func) xs = ode(x0[i:i+1], times[:, i:i+1], return_whole_sequence=True) xs_list.append(xs) orig_trajs = torch.cat(xs_list, dim=1).detach() samp_trajs = orig_trajs + torch.randn_like(orig_trajs) * noise_std samp_ts = times fig, axes = plt.subplots(nrows=3, ncols=3, figsize=(15, 9)) axes = axes.flatten() for i, ax in enumerate(axes): ax.scatter(samp_trajs[:, i, 0], samp_trajs[:, i, 1], c=samp_ts[:, i, 0], cmap=cm.plasma) plt.show() import numpy.random as npr def gen_batch(batch_size, n_sample=100): n_batches = samp_trajs.shape[1] // batch_size time_len = samp_trajs.shape[0] n_sample = min(n_sample, time_len) for i in range(n_batches): if n_sample > 0: probs = [1. / (time_len - n_sample)] * (time_len - n_sample) t0_idx = npr.multinomial(1, probs) t0_idx = np.argmax(t0_idx) tM_idx = t0_idx + n_sample else: t0_idx = 0 tM_idx = time_len frm, to = batch_size*i, batch_size*(i+1) yield samp_trajs[t0_idx:tM_idx, frm:to], samp_ts[t0_idx:tM_idx, frm:to]

Treinamento

 vae = ODEVAE(2, 64, 6) vae = vae.cuda() if use_cuda: vae = vae.cuda() optim = torch.optim.Adam(vae.parameters(), betas=(0.9, 0.999), lr=0.001) preload = False n_epochs = 20000 batch_size = 100 plot_traj_idx = 1 plot_traj = orig_trajs[:, plot_traj_idx:plot_traj_idx+1] plot_obs = samp_trajs[:, plot_traj_idx:plot_traj_idx+1] plot_ts = samp_ts[:, plot_traj_idx:plot_traj_idx+1] if use_cuda: plot_traj = plot_traj.cuda() plot_obs = plot_obs.cuda() plot_ts = plot_ts.cuda() if preload: vae.load_state_dict(torch.load("models/vae_spirals.sd")) for epoch_idx in range(n_epochs): losses = [] train_iter = gen_batch(batch_size) for x, t in train_iter: optim.zero_grad() if use_cuda: x, t = x.cuda(), t.cuda() max_len = np.random.choice([30, 50, 100]) permutation = np.random.permutation(t.shape[0]) np.random.shuffle(permutation) permutation = np.sort(permutation[:max_len]) x, t = x[permutation], t[permutation] x_p, z, z_mean, z_log_var = vae(x, t) z_var = torch.exp(z_log_var) kl_loss = -0.5 * torch.sum(1 + z_log_var - z_mean**2 - z_var, -1) loss = 0.5 * ((x-x_p)**2).sum(-1).sum(0) / noise_std**2 + kl_loss loss = torch.mean(loss) loss /= max_len loss.backward() optim.step() losses.append(loss.item()) print(f"Epoch {epoch_idx}") frm, to, to_seed = 0, 200, 50 seed_trajs = samp_trajs[frm:to_seed] ts = samp_ts[frm:to] if use_cuda: seed_trajs = seed_trajs.cuda() ts = ts.cuda() samp_trajs_p = to_np(vae.generate_with_seed(seed_trajs, ts)) fig, axes = plt.subplots(nrows=3, ncols=3, figsize=(15, 9)) axes = axes.flatten() for i, ax in enumerate(axes): ax.scatter(to_np(seed_trajs[:, i, 0]), to_np(seed_trajs[:, i, 1]), c=to_np(ts[frm:to_seed, i, 0]), cmap=cm.plasma) ax.plot(to_np(orig_trajs[frm:to, i, 0]), to_np(orig_trajs[frm:to, i, 1])) ax.plot(samp_trajs_p[:, i, 0], samp_trajs_p[:, i, 1]) plt.show() print(np.mean(losses), np.median(losses)) clear_output(wait=True) spiral_0_idx = 3 spiral_1_idx = 6 homotopy_p = Tensor(np.linspace(0., 1., 10)[:, None]) vae = vae if use_cuda: homotopy_p = homotopy_p.cuda() vae = vae.cuda() spiral_0 = orig_trajs[:, spiral_0_idx:spiral_0_idx+1, :] spiral_1 = orig_trajs[:, spiral_1_idx:spiral_1_idx+1, :] ts_0 = samp_ts[:, spiral_0_idx:spiral_0_idx+1, :] ts_1 = samp_ts[:, spiral_1_idx:spiral_1_idx+1, :] if use_cuda: spiral_0, ts_0 = spiral_0.cuda(), ts_0.cuda() spiral_1, ts_1 = spiral_1.cuda(), ts_1.cuda() z_cw, _ = vae.encoder(spiral_0, ts_0) z_cc, _ = vae.encoder(spiral_1, ts_1) homotopy_z = z_cw * (1 - homotopy_p) + z_cc * homotopy_p t = torch.from_numpy(np.linspace(0, 6*np.pi, 200)) t = t[:, None].expand(200, 10)[:, :, None].cuda() t = t.cuda() if use_cuda else t hom_gen_trajs = vae.decoder(homotopy_z, t) fig, axes = plt.subplots(nrows=2, ncols=5, figsize=(15, 5)) axes = axes.flatten() for i, ax in enumerate(axes): ax.plot(to_np(hom_gen_trajs[:, i, 0]), to_np(hom_gen_trajs[:, i, 1])) plt.show() torch.save(vae.state_dict(), "models/vae_spirals.sd")

É o que acontece depois de uma noite de treinamento

Pontos são observações ruidosas da trajetória original (azul), o
amarelo é reconstruído e trajetórias interpoladas, usando pontos como entradas.

A cor do ponto mostra o tempo.

As reconstruções de alguns exemplos não parecem muito boas. Talvez o modelo não seja suficientemente complexo ou não seja estudado por tempo suficiente. De qualquer forma, a reconstrução parece bastante razoável.

Agora vamos ver o que acontece se interpolarmos uma variável oculta em uma trajetória no sentido horário para uma trajetória no sentido anti-horário.

Os autores também comparam reconstruções e interpolações de caminho entre o ODE Neural e uma rede recursiva simples.

Ilustração do artigo original.

Fluxos de normalização contínua

O artigo original também traz muito para o tópico Normalização de fluxos. Os fluxos de normalização são usados quando você precisa coletar amostras de alguma distribuição complexa que aparece através de uma alteração de variáveis de uma distribuição simples (gaussiana, por exemplo), e ainda conhece a densidade de probabilidade no ponto de cada amostra.
Os autores mostram que o uso de substituição contínua de variáveis é muito mais eficiente em termos de computação e interpretável que os métodos anteriores.

Os fluxos de normalização são muito úteis em modelos como AutoCoders de Variação , Redes Neurais Bayesianas e outros da abordagem bayesiana.

Este tópico, no entanto, está fora do escopo desteartigos e os interessados devem ler o artigo científico original.

Para sementes:

Visualização da transformação de ruído (distribuição simples) em dados (distribuição complexa) para dois conjuntos de dados;

O eixo X mostra a transformação da densidade e das amostras ao longo do "tempo" (para NS) e "profundidade" (para NS).

Ilustração do artigo original.

Agradecimentos ao bekemax pela ajuda na edição da versão em inglês do texto e por comentários físicos interessantes.

Isso conclui minha pequena pesquisa sobre EDOs Neurais . Obrigado pela atenção!

Apresentando ODE Neural

Equações diferenciais ordinárias neurais

Declaração do problema

Implementação

Aplicação

Recuperação da função dinâmica real (verificação de abordagem)

ODE neural inspirado em ResNets

Validando a arquitetura Neural ODE no MNIST

Função Generativa Oculta para Modelagem de Séries Temporais

Dados

VAE como modelo generativo

Definir modelos

Geração de conjunto de dados

Treinamento

Fluxos de normalização contínua

Links úteis

More articles: