Tarefas do livro escolar II

Parte I
Parte II
Parte III

Este artigo discute o método de estimar o intervalo de valores aceitos e o relacionamento desse método com tarefas que contêm um módulo.

Ao resolver alguns problemas, é necessário considerar o intervalo dentro do qual o valor desejado pode estar.

Considere o método de estimativa para resolver desigualdades.

Suponha que o preço por unidade de mercadorias possa variar de 5 a 10 RUB. Atribuir um limite superior significa determinar o valor máximo que a quantidade desejada pode receber. Para duas unidades de mercadorias cujo preço não excede 10, a estimativa superior será 10 + 10 = 20 .

Considere o problema no perfil do perfil do problema MI Bashmakova
37. Estimativas conhecidas para variáveis $$$x$ e$$ $ inline $ y: 0 <x <5, 2 <y <3. $ inline $

Dê as melhores notas para as seguintes expressões:
1 $$$2x + 3y$
2) $$$xy$

5) $$$\ frac {1} {y}$
6 $$$\ frac {x} {y}$

8) $$$x-y$
9 $$$3x-2y$


Em geral, a análise de quantidades infinitesimais usa um critério de avaliação. Um módulo (como vizinhança) encontra aplicação na definição de um limite.

$$$$ display $$ \ left | x_ {n} -a \ right | <\ varepsilon $$ display $$

Considere o exemplo do "Curso de cálculo diferencial e integral" 363 (6)

Fácil de definir divergência de linha

$$

$$\ sum \ frac {1} {\ sqrt {n}} = 1+ \ frac {1} {\ sqrt {2}} + \ frac {1} {\ sqrt {3}} + ... + \ frac {1} {\ sqrt {n}} + ...$$

De fato, uma vez que seus membros diminuem, a enésima soma parcial

$$exibição $$ $$ 1+ \ frac {1} {\ sqrt {2}} + ... + \ frac {1} {\ sqrt {n}}> n \ cdot \ frac {1} {\ sqrt {n }} = \ sqrt {n} $$ exibir $$

e cresce ad infinitum com $$$n$ .

Para provar que $$$1+ \ frac {1} {\ sqrt {2}} + ... + \ frac {1} {\ sqrt {n}}$ realmente mais $$$\ sqrt {n}$ , você precisa fazer uma estimativa mais baixa dessa expressão. Obtemos o sistema de desigualdades

$$exibição $$ $$ \ esquerda \ {\! \ begin {align} e \ frac {1} {\ sqrt {n-1}}> \ frac {1} {\ sqrt {n}} \\ & frac { 1} {\ sqrt {n-2}}> \ frac {1} {\ sqrt {n}} \\ & \ frac {1} {\ sqrt {n-3}}> \ frac {1} {\ sqrt {n}} \\ & ... \ end {alinhado} \ right. $$ display $$

Depois de adicionar todas as desigualdades deste sistema, obtemos

$$$$ display $$ 1+ \ frac {1} {\ sqrt {2}} + \ frac {1} {\ sqrt {3}} + ... + \ frac {1} {\ sqrt {n}}> \ frac {1} {\ sqrt {n}} + \ frac {1} {\ sqrt {n}} + \ frac {1} {\ sqrt {n}} + ... + \ frac {1} {\ sqrt {n}} = n \ cdot \ frac {1} {\ sqrt {n}} $$ display $$

Isso prova que essa série diverge.

Para uma série harmônica, esse método não funciona, porque $$$n$ série harmônica parcial parcial

$$$$ display $$ 1+ \ frac {1} {2} + \ frac {1} {3} + ... + \ frac {1} {n}> n \ cdot \ frac {1} {n} = 1 $$ exibição $$

Voltar para a tarefa

38. Calcular a quantidade ("Tarefas para crianças de 5 a 15 anos")

$$

$$\ frac {1} {1 \ cdot2} + \ frac {1} {2 \ cdot3} + \ frac {1} {3 \ cdot4} + ... + \ frac {1} {99 \ cdot100}$$

(com um erro não superior a 1% da resposta)

Melhor estimativa da série $$$\ frac {n} {n + 1}$ dá o número 1.

Abandone o primeiro mandato $$$\ frac {1} {1 \ cdot2}$

(define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* (+ n 1.0 )(+ n 2.0))) (series_sum_1(- n 1.0))) ) ) ) (writeln (series_sum_1 10)) (writeln (series_sum_1 100)) (writeln (series_sum_1 1000)) (writeln (series_sum_1 10000)) (writeln (series_sum_1 100000)) (writeln (series_sum_1 1000000)) 

Nós temos $$$1 - \ frac {1} {1 \ cdot2} = \ frac {1} {2}$
0.4166666666666666363
0.49019607843137253
0.4990019960079833
0.4999000199960005
0.49999000019998724
0.4999990000019941

Você pode conferir ideone.com aqui


Solte os dois primeiros termos $$$\ frac {1} {1 \ cdot2} + \ frac {1} {2 \ cdot3}$

 (define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* (+ n 2.0) (+ n 3.0))) (series_sum_1(- n 1.0))) ) ) ) (series_sum_1 1000000) 

Nós vamos obter 0.33333233333632745
Somas parciais da série são delimitadas acima.

A linha positiva sempre tem uma quantidade; essa soma será finita (e, portanto, a série convergente) se as somas parciais da série forem delimitadas acima, e infinita (e a série divergente) caso contrário.

Jogue fora $$$n$ termos iniciais da série harmônica.
Prove (usando o limite inferior) que

$$exibição $$ $$ \ frac {1} {n + 1} + \ frac {1} {n + 2} + ... + \ frac {1} {2n}> \ frac {1} {2} $$ exibir $$

Se, descartando os dois primeiros termos, os membros restantes da série harmônica são divididos em grupos por $$$2,4,8, ..., 2 ^ {k-1}, ...$ membros em cada

$$

$$\ frac {1} {3} + \ frac {1} {4}; \ frac {1} {5} + \ frac {1} {6} + \ frac {1} {7} + \ frac {1} {8}; \ frac {1} {9} + ... \ frac {1} {16}; ...;$$

$$

$$\ frac {1} {2 ^ {k-1} +1} + ... + \ frac {1} {2 ^ {k}}; ...,$$

então cada um desses valores individualmente será maior $$$\ frac {1} {2}$ .
... Vemos que somas parciais não podem ser delimitadas acima: a série tem uma soma infinita.

Calculamos os valores parciais que são obtidos descartando $$$2 ^ {k}$ termos.

 #lang racket (* 1.0 (+ 1/3 1/4)) (* 1.0 (+ 1/5 1/6 1/7 1/8)) (* 1.0 (+ 1/9 1/10 1/11 1/12 1/13 1/14 1/15 1/16)) 

Temos:
0.583333333333333434
0.6345238095238095
0.6628718503718504
Escrevemos um programa que calcula a soma das séries harmônicas de $$$\ frac {n} {2}$ antes $$$n$ onde $$$n = 2 ^ {k}$ às $$$k \ in \ mathbb {N}$

 #lang racket (define (Hn n ) (define half_arg (/ n 2.0)) (define (series_sum n) (if (= n half_arg ) 0 (+ (/ 1.0 n) (series_sum(- n 1)) ) ) ) (series_sum n) ) (Hn 4) (Hn 8) (Hn 16) (Hn 32) 

Temos:
0.583333333333333333
0.6345238095238095
0.6628718503718504
0.6777662022075267

Você pode fazer o check-in de ide online no link
Para alcance $$$\ left [1 + 2 ^ {70}; 2 ^ {71} \ right]$ temos 0,693147 ...
Confira mojo na Wolfram Cloud aqui .

Esse algoritmo recursivo causa um estouro rápido da pilha.
Este artigo tem um exemplo de cálculo de fatorial usando um algoritmo iterativo. Modificamos esse algoritmo iterativo para calcular a soma parcial Hn dentro de certos limites; chame esses limites de aeb

 (define (Hn ab) (define (iteration product counter) (if (> counter b) product (iteration (+ product (/ 1.0 counter)) (+ counter 1)))) (iteration 0 a)) 

O limite inferior é o número $$$1 + 2 ^ {k}$ , o limite superior é o número $$$2 \ cdot 2 ^ {k}$
Escrevemos uma função que calcula a potência de dois

 (define (power_of_two k) (define (iteration product counter) (if (> counter k) product (iteration (* product 2) (+ counter 1)))) (iteration 1 1)) 

Substituiremos (+ 1 (power_of_two k)) como limite inferior e usaremos a função (* 2 (power_of_two k)) ou sua função equivalente (power_of_two (+ 1 k)) como limite superior
Reescreva a função Hn

 (define (Hn k) (define a (+ 1 (power_of_two k)) ) (define b (* 2 (power_of_two k)) ) (define (iteration product counter) (if (> counter b) product (iteration (+ product (/ 1.0 counter)) (+ counter 1)))) (iteration 0 a )) 

Agora você pode calcular Hn para valores grandes $$$k$ .

Escrevemos em C um programa que mede o tempo necessário para calcular o Hn . Usaremos a função clock () da biblioteca padrão <time.h>
Um artigo sobre como medir o tempo do processador está em Habré aqui .

 #include <math.h> #include <stdio.h> #include <time.h> int main(int argc, char **argv) { double count; // k  1+2^30  2^31 for(unsigned long long int i=1073741825 ;i<=2147483648 ;i++) { count=count+1.0/i; } printf("Hn = %.12f ", count); double seconds = clock() / (double) CLOCKS_PER_SEC; printf("  %f  \n", seconds); return 0; } 

Geralmente, o ide online limita o tempo de execução dos programas em execução a cinco segundos, portanto esse programa pode ser verificado apenas em alguns ide online, por exemplo, onlinegdb.com ou repl.it
Para k de 1 + 2 ^ 30 a 2 ^ 31, o tempo de operação será de ~ 5 segundos.
Para k de 1 + 2 ^ 31 a 2 ^ 32, o tempo de operação será de ~ 10 segundos.
Para k de 1 + 2 ^ 32 a 2 ^ 33, o tempo de operação será de ~ 20 segundos.
Para k de 1 + 2 ^ 33 a 2 ^ 34, o tempo de operação será de ~ 40 segundos.
Para k de 1 + 2 ^ 34 a 2 ^ 35, o tempo de operação será mais de um minuto.
...
Para k de 1 + 2 ^ 45 a 2 ^ 46, o tempo de operação será superior a 24 horas.

Suponha que para k de 1 + 2 ^ 30 a 2 ^ 31, o tempo de execução do algoritmo seja ~ 2 segundos.
Então, para k = 2 ^ (30 + n), o tempo de execução do algoritmo é 2 ^ n seg. (em $$$n \ in \ mathbb {N}$ )
Este algoritmo tem complexidade exponencial .

Voltar para os módulos.
No cálculo integral, o módulo é usado na fórmula

$$

$$\ int \ frac {1} {x} dx = \ int \ frac {dx} {x} = ln \ esquerda | x \ right | + C$$

Em Habré, havia um artigo O logaritmo mais natural em que essa integral é considerada e com base em seu cálculo do número $$$e$ .

A presença do módulo na fórmula $$$\ int \ frac {dx} {x} = ln \ esquerda | x \ right | + C$ mais substanciado no "Curso de cálculo diferencial e integral"

Se ...$$ $ inline $ x <0 $ inline $ , então, por diferenciação, é fácil verificar se $$$\ left [ln (-x) \ right] '= \ frac {1} {x}$

Aplicação física da integral $$$\ int \ frac {dx} {x}$

Essa integral é usada para calcular a diferença de potencial das placas de um capacitor cilíndrico.


"Eletricidade e magnetismo":

A diferença de potencial entre as placas é encontrada pela integração:

$$

$$\ varphi_ {1} - \ varphi_ {2} = \ int \ limits_ {R_ {1}} ^ {R_ {2}} E (r) dr = \ frac {q} {2 \ pi \ varepsilon_ {0} \ varepsilon l} \ int \ limits_ {R_ {1}} ^ {R_ {2}} \ frac {dr} {r} = \ frac {q} {2 \ pi \ varepsilon_ {0} \ varepsilon l} \ frac {R_ {2}} {R_ {1}}$$

( $$$R_ {1}$ e $$$R_ {2}$ - os raios das placas interna e externa).

O sinal do módulo não é usado aqui sob o sinal do logaritmo natural $$$ln \ esquerda | \ frac {R_ {2}} {R_ {1}} \ right |$ porque $$$R_ {1}$ e $$$R_ {2}$ estritamente positivo e essa forma de gravação é redundante.

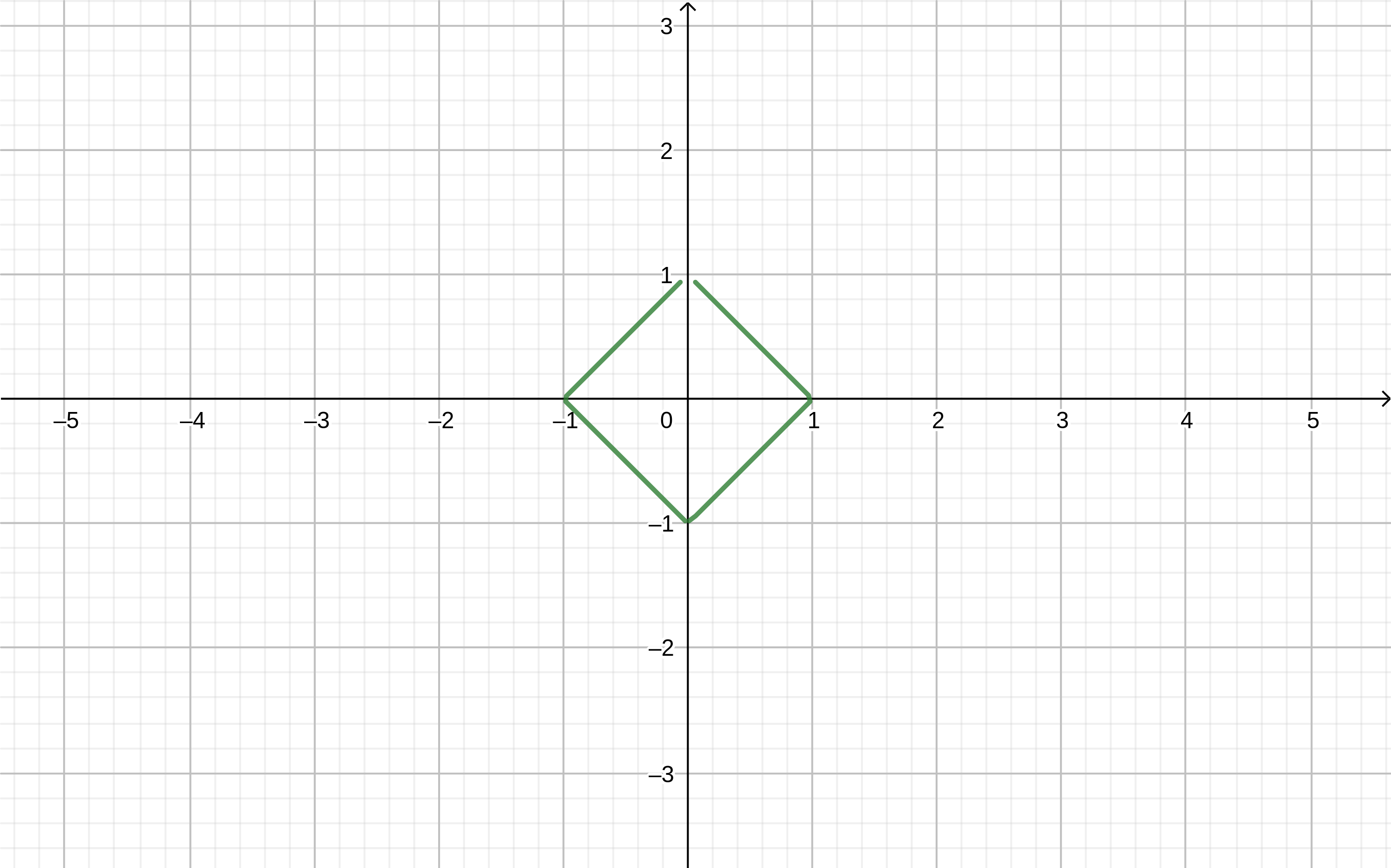
Desenho "modular"

Usando módulos, você pode desenhar várias formas.

Se no programa geogebra , escreva a fórmula $$$abs (x) + abs (y) = 1$ nós temos



Você pode desenhar formas mais complexas. Vamos desenhar, por exemplo, uma "borboleta" na nuvem WolframAlpha

$$

$$\ sum \ frac {\ left | x \ right | } {n- \ esquerda | x \ right | } + \ frac {\ left | x + n \ direita | } {n} + \ frac {\ left | x-n \ direita | } {n}$$

Traçar [Soma [abs (x) / (n-abs (x)) + abs (x + n) / (n) + abs (xn) / (n), {n, 1,20}], {x, -60,60}]
Nessa expressão $$$n$ encontra-se na faixa de $$$1$ antes $$$20$ , $$$x$ encontra-se na faixa de $$$-60$ antes $$$60$ .
Link para a imagem.

Livros:

"O livro de tarefas de orientação de perfil" M.I. Bashmakov
Curso geral de física: em 3 volumes T. 2. "Eletricidade e magnetismo" I.V. Savelyev