Olá Habr! Trago a sua atenção uma tradução do artigo de Rudy Gilman e Katherine Wang RL intuitiva: Introdução ao Advantage-Actor-Critic (A2C) .

Os Especialistas em Aprendizado Reforçado (RL) produziram muitos tutoriais excelentes. A maioria, no entanto, descreve RL em termos de equações matemáticas e diagramas abstratos. Gostamos de pensar sobre o assunto de uma perspectiva diferente. A própria RL é inspirada na maneira como os animais aprendem; então, por que não converter o mecanismo subjacente da RL novamente em fenômenos naturais que ele pretende simular? As pessoas aprendem melhor através de histórias.
Esta é a história do modelo Actor Advantage Critic (A2C). O modelo sujeito-crítico é uma forma popular do modelo Gradiente de Política, que por si só é um algoritmo tradicional de RL. Se você entende A2C, entende RL profunda.
Depois de obter uma compreensão intuitiva do A2C, verifique:
Ilustrações @embermarke
Em RL, o agente, a raposa Klyukovka, percorre estados cercados por ações, tentando maximizar as recompensas ao longo do caminho.
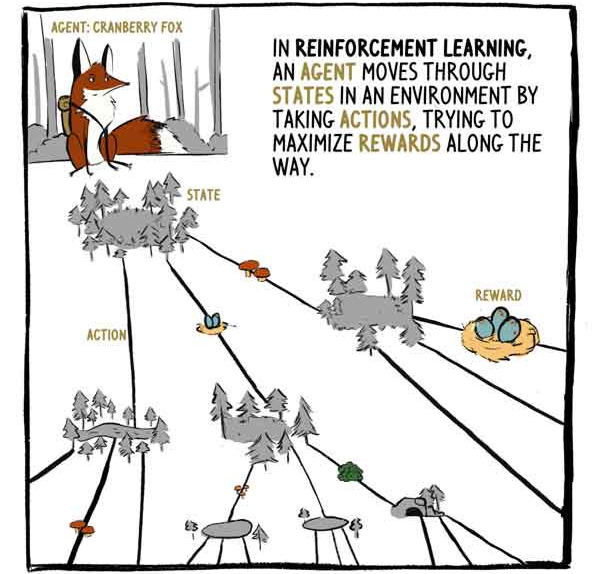
A2C recebe entradas de status - entradas de sensor no caso de Klukovka - e gera duas saídas:
1) Uma avaliação de quanto a remuneração será recebida, a partir do momento do estado atual, com exceção da remuneração atual (existente).
2) Uma recomendação sobre que ação tomar (política).
Crítico: uau, que vale maravilhoso! Será um dia frutífero para forragear! Aposto que hoje colecionarei 20 pontos antes do pôr do sol.
"Assunto": essas flores estão lindas, sinto um desejo por "A".

Os modelos Deep RL são máquinas de mapeamento de entrada e saída, como qualquer outro modelo de classificação ou regressão. Em vez de categorizar imagens ou texto, os modelos RL profundos levam estados a ações e / ou estados a valores de estado. A2C faz as duas coisas.


Esse conjunto de recompensa-ação-estado é uma observação. Ela escreverá essa linha de dados em seu diário, mas ainda não pensará nisso. Ela o preencherá quando parar para pensar.
Alguns autores associam a recompensa 1 à etapa 1 do tempo, outros a associam à etapa 2, mas todos têm em mente o mesmo conceito: a recompensa está relacionada ao estado e a ação imediatamente o precede.

Enganchar repete o processo novamente. Primeiro, ela percebe seu entorno e desenvolve uma função V (S) e uma recomendação de ação.
Crítico: Este vale parece bastante padrão. V (S) = 19.
Assunto: As opções de ação são muito semelhantes. Eu acho que vou apenas na pista "C".
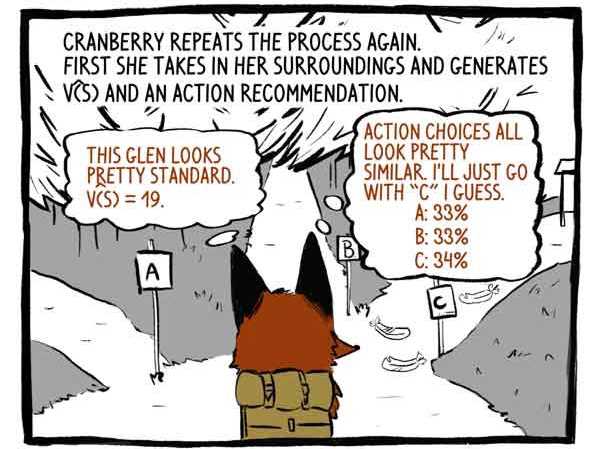
Então ele age.

Recebe uma recompensa de +20! E registra a observação.

Ela repete o processo novamente.

Depois de coletar três observações, Klyukovka pára para pensar.
Outras famílias de modelos esperam até o final do dia (Monte Carlo), enquanto outras pensam após cada etapa (uma etapa).
Antes que ela possa estabelecer sua crítica interna, Klukovka precisa calcular quantos pontos ela realmente receberá em cada estado.
Mas primeiro!
Vejamos como a prima de Klukovka, Lis Monte Carlo, calcula o verdadeiro significado de cada estado.
Os modelos de Monte Carlo não refletem sua experiência até o final do jogo e, como o valor do último estado é zero, é muito simples encontrar o verdadeiro valor desse estado anterior como a soma das recompensas recebidas após esse momento.
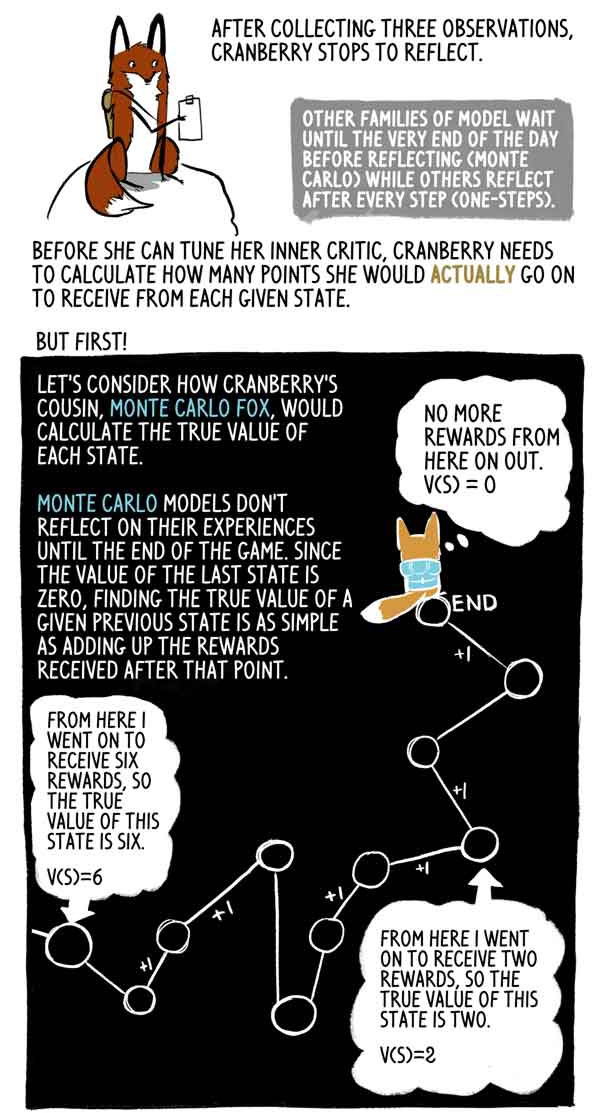
De fato, esta é apenas uma amostra de alta dispersão V (S). O agente poderia facilmente seguir uma trajetória diferente do mesmo estado, recebendo assim uma recompensa agregada diferente.
Mas Klyukovka vai, para e reflete muitas vezes até o dia chegar ao fim. Ela quer saber quantos pontos ela realmente receberá de cada estado até o final do jogo, porque faltam várias horas para o final do jogo.
É aí que ela faz algo realmente inteligente - a raposa Klyukovka estima quantos pontos receberá pelo último estado neste conjunto. Felizmente, ela tem uma avaliação correta de sua condição - sua crítica.
Com essa avaliação, Klyukovka pode calcular os valores "corretos" dos estados anteriores exatamente como a raposa de Monte Carlo.
Lis Monte Carlo avalia as marcas de alvo, realizando a trajetória e acrescentando recompensas a partir de cada estado. A2C corta essa trajetória e a substitui por uma avaliação de seu crítico. Essa carga inicial reduz a variação da pontuação e permite que o A2C seja executado continuamente, embora introduzindo um pequeno viés.

As recompensas são muitas vezes reduzidas para refletir o fato de que a remuneração é agora melhor do que no futuro. Por uma questão de simplicidade, Klukovka não reduz suas recompensas.

O Klukovka agora pode percorrer cada linha de dados e comparar suas estimativas de valores de estado com seus valores reais. Ela usa a diferença entre esses números para aperfeiçoar suas habilidades de previsão. A cada três etapas ao longo do dia, Klyukovka coleta uma experiência valiosa que vale a pena considerar.
“Classifiquei mal os estados 1 e 2. O que fiz de errado? Sim! A próxima vez que eu ver penas como essas, aumentarei V (S).
Pode parecer louco que Klukovka seja capaz de usar sua classificação V (S) como base para compará-la com outras previsões. Mas os animais (incluindo nós) fazem isso o tempo todo! Se você acha que as coisas estão indo bem, não precisa treinar novamente as ações que o levaram a esse estado.

Cortando nossas saídas calculadas e substituindo-as por uma estimativa de carga inicial, substituímos a grande variação de Monte Carlo por uma pequena inclinação. Os modelos de RL normalmente sofrem de alta dispersão (representando todos os caminhos possíveis), e essa substituição geralmente vale a pena.
Klukovka repete esse processo o dia todo, coletando três observações de recompensa de ação-estado e refletindo sobre elas.
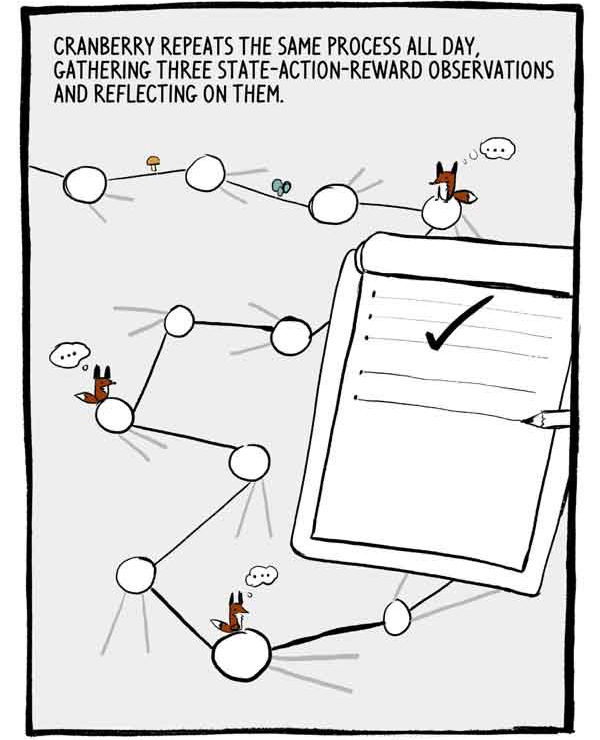
Cada conjunto de três observações é uma pequena série autocorrelacionada de dados de treinamento rotulados. Para reduzir essa autocorrelação, muitos A2Cs treinam muitos agentes em paralelo, somando sua experiência antes de enviá-la para uma rede neural comum.

O dia está finalmente chegando ao fim. Apenas dois passos restantes.
Como dissemos anteriormente, as recomendações das ações de Klukovka são expressas em porcentagem de confiança sobre suas capacidades. Em vez de apenas escolher a opção mais confiável, Klukovka escolhe essa distribuição de ações. Isso garante que ela nem sempre aceite ações seguras, mas potencialmente medíocres.
Eu poderia me arrepender, mas ... Às vezes, explorando coisas desconhecidas, você pode chegar a novas descobertas emocionantes ...

Para incentivar ainda mais a pesquisa, um valor chamado entropia é subtraído da função de perda. Entropia significa o "escopo" da distribuição de ações.
- Parece que o jogo valeu a pena!

Ou não?
Às vezes, o agente está em um estado em que todas as ações levam a resultados negativos. A2C, no entanto, lida bem com situações ruins.


Quando o sol se pôs, Klyukovka refletiu sobre o último conjunto de soluções.

Conversamos sobre como Klyukovka cria seu crítico interno. Mas como ela ajusta seu "sujeito" interno? Como ela aprende a fazer escolhas tão requintadas?
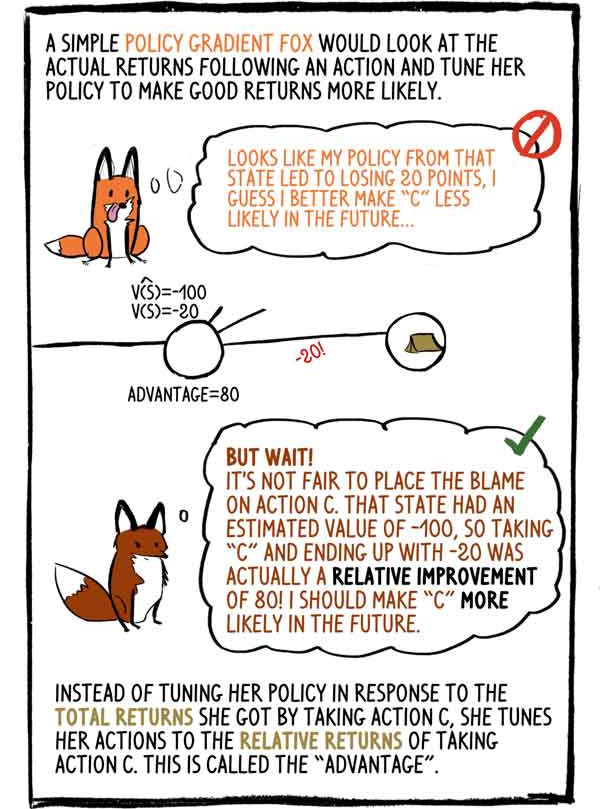
A política gradiente-raposa de mente simples examinaria a renda real após a ação e ajustaria sua política para aumentar a probabilidade de uma boa renda: - Parece que minha política nesse estado levou a uma perda de 20 pontos, acho que no futuro é melhor fazer "C" menos provável.
- Mas espera! É injusto culpar a ação "C". Esse estado tinha um valor estimado de -100, portanto, escolher "C" e terminar com -20 foi na verdade uma melhoria relativa de 80! Eu tenho que tornar "C" mais provável no futuro.
Em vez de ajustar sua política em resposta à receita total que recebeu ao selecionar a ação C, ela ajusta sua ação às receitas relativas da ação C. Isso é chamado de “vantagem”.
O que chamamos de vantagem é simplesmente um erro. Como vantagem, Klukovka o usa para tornar mais surpreendentemente boas atividades surpreendentemente boas. Por engano, ela usa a mesma quantia para pressionar seu crítico interno para melhorar sua avaliação do valor do status.
O sujeito tira proveito de:
- "Uau, isso funcionou melhor do que eu pensava, a ação C deve ser uma boa idéia."
O crítico usa o erro:
“Mas por que fiquei surpresa? Provavelmente não deveria ter avaliado essa condição tão negativamente. "
Agora podemos mostrar como as perdas totais são calculadas - minimizamos essa função para melhorar nosso modelo.
“Perda total = perda de ação + perda de valor - entropia”
Observe que, para calcular os gradientes de três tipos qualitativamente diferentes, consideramos os valores "através de um". Isso é eficaz, mas pode dificultar a convergência.

Como todos os animais, à medida que Klyukovka envelhece, ele aprimora sua capacidade de prever os valores dos estados, ganha mais confiança em suas ações e menos frequentemente se surpreende com os prêmios.
Os agentes de RL, como Klukovka, não apenas geram todos os dados necessários, simplesmente interagindo com o ambiente, mas também avaliam os próprios rótulos de destino. É isso mesmo, os modelos RL atualizam as notas anteriores para corresponder melhor às notas novas e melhoradas.
Como o Dr. David Silver, chefe do grupo de RL do Google Deepmind, diz: AI = DL + RL. Quando um agente como Klyukovka pode definir sua própria inteligência, as possibilidades são infinitas ...
