O livro “Algoritmo Perfeito. O básico

Oi, habrozhiteli! Este livro é baseado nos cursos algorítmicos on-line que Tim Rafgarden ministra no Coursera e Stanford Lagunita, e esses cursos surgiram graças às palestras que ele vem dando aos estudantes da Universidade de Stanford há muitos anos.

Algoritmos são o coração e a alma da ciência da computação. Você não pode ficar sem eles, eles estão por toda parte - desde roteamento de rede e cálculos genômicos até criptografia e aprendizado de máquina. O "Algoritmo Perfeito" o transformará em um verdadeiro profissional que definirá tarefas e as solucionará com maestria na vida e em uma entrevista ao contratar qualquer empresa de TI. Tim Rafgarden falará sobre análise assintótica, notação O-grande, algoritmos de divisão e conquista, randomização, classificação e seleção. O livro é dirigido a quem já possui experiência em programação. Você passará para um novo nível para ver o panorama geral, entender os conceitos de baixo nível e as nuances matemáticas.

* 6.3. DSelecione o algoritmo

O algoritmo RSelect é executado em tempo linear para cada entrada, na qual a expectativa matemática está associada a escolhas aleatórias executadas pelo algoritmo. A randomização é necessária para a seleção linear? Nesta seção e mais, esse problema é resolvido usando um algoritmo linear determinístico para o problema de escolha.

Para a tarefa de classificação, o tempo de execução médio do algoritmo QuickSort aleatório O (n log n) é igual ao algoritmo determinístico MergeSort, e ambos os algoritmos QuickSort e MergeSort são algoritmos úteis para uso prático. Por outro lado, embora o algoritmo de seleção linear determinístico descrito nesta seção funcione bem na prática, ele não compete com o algoritmo RSelect. Isso acontece por duas razões: devido aos grandes fatores constantes no tempo de operação do algoritmo DSelect e ao trabalho realizado pelo algoritmo associado à alocação e gerenciamento de RAM adicional. No entanto, as idéias do algoritmo são tão legais que não posso deixar de contar sobre elas.

6.3.1 Idéia brilhante: mediana de medianas

O algoritmo RSelect é rápido, porque existe uma alta probabilidade de que os elementos de suporte aleatório sejam bastante bons, fornecendo uma divisão aproximadamente equilibrada da matriz de entrada após a separação; além disso, bons elementos de suporte progridem rapidamente. Se não podemos usar a randomização, como podemos calcular um bom elemento de referência sem fazer muito trabalho?

A idéia engenhosa de uma escolha linear determinística é usar a "mediana das medianas" como proxy da verdadeira mediana. O algoritmo considera os elementos da matriz de entrada como equipes esportivas e realiza um torneio eliminatório em duas rodadas, cujo campeão é o elemento de apoio; veja também a fig. 6.1


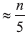
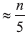
A primeira rodada é uma fase de grupo com elementos nas posições 1 a 5 da matriz de entrada como o primeiro grupo, elementos nas posições 6 a 10 como o segundo grupo e assim por diante. O vencedor da primeira rodada de um grupo de cinco elementos é definido como a mediana do elemento (ou seja, o terceiro menor). Uma vez que existe grupos de cinco elementos, existem primeiros vencedores. (Como sempre, ignoramos frações por simplicidade.) Um campeão de torneio é definido como a mediana dos vencedores da primeira rodada.

6.3.2 Pseudocódigo para o algoritmo DSelect

Como realmente calcular a mediana das medianas? A implementação da primeira etapa do torneio de eliminação é simples, uma vez que cada cálculo da mediana inclui apenas cinco elementos. Por exemplo, cada um desses cálculos pode ser realizado por força bruta (para cada uma das cinco possibilidades, verifique em detalhes se é um elemento do meio) ou usando nossas informações sobre o problema de classificação (seção 6.1.2). 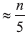Para implementar o segundo estágio, calculamos a mediana de vencedores da primeira rodada recursivamente.


As linhas 1–2 e 6–13 são idênticas ao algoritmo RSelect. As linhas 3 a 5 são a única parte nova do algoritmo; eles calculam a mediana da mediana da matriz de entrada, substituindo a linha no algoritmo RSelect, que seleciona o elemento de referência aleatoriamente.

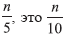
As linhas 3 e 4 calculam os vencedores da primeira rodada do torneio de eliminação, onde o elemento do meio de cada grupo de cinco elementos é calculado usando o método de força bruta ou o algoritmo de classificação e copia esses vencedores para o novo array C. A linha 5 calcula o campeão do torneio calculando recursivamente a mediana do array C; desde C tem um comprimento (provisoriamente) -ª estatística ordinal da matriz C. Nenhuma randomização é usada em nenhuma etapa do algoritmo.

6.3.3 Compreendendo o algoritmo DSelect

Uma chamada recursiva ao algoritmo DSelect ao calcular um elemento de referência pode parecer perigosamente cíclica. Para entender o que está acontecendo, primeiro designemos o número total de chamadas recursivas.


A resposta correta é: (c). Descartando o caso base e o caso feliz em que o elemento de referência são as estatísticas de pedidos necessárias, o algoritmo DSelect faz duas chamadas recursivas. Para entender o porquê, não exagere; basta verificar o pseudocódigo do algoritmo DSelect linha por linha. A linha 5 tem uma chamada recursiva e outra na linha 11 ou 13.

Há duas perguntas comuns confusas sobre essas duas chamadas recursivas. Primeiro, não é fato que o algoritmo RSelect faça apenas uma chamada recursiva, a razão pela qual ele funciona mais rápido que nossos algoritmos de classificação? O DSelect não abandona essa melhoria fazendo duas chamadas recursivas? A Seção 6.4 mostra que, como a chamada extra recursiva na linha 5 deve resolver apenas uma subtarefa relativamente pequena (com 20% dos elementos na matriz original), ainda podemos salvar a análise linear.

Em segundo lugar, duas chamadas recursivas desempenham papéis fundamentalmente diferentes. O objetivo da chamada recursiva na linha 5 é determinar um bom elemento de referência para a chamada recursiva atual. O objetivo da chamada recursiva na linha 11 ou 13 é o usual - resolver recursivamente a tarefa restante menor deixada pela chamada recursiva atual. No entanto, a estrutura recursiva no algoritmo DSelect segue completamente a tradição de todos os outros algoritmos de divisão e conquista que estudamos: cada chamada recursiva faz um pequeno número de chamadas recursivas subsequentes com subtarefas estritamente mais refinadas e faz algum trabalho extra. Se não estivéssemos preocupados com o fato de algoritmos como MergeSort ou QuickSort funcionarem para sempre, não devemos nos preocupar com o algoritmo DSelect.

6.3.4 Tempo de execução do algoritmo DSelect

O algoritmo DSelect não é apenas um programa bem definido que é concluído em uma quantidade limitada de tempo - ele é executado em tempo linear, realizando mais trabalhos apenas em um fator constante do que o necessário para ler os dados de entrada.

Teorema 6.6 (tempo de operação do algoritmo DSelect). Para cada matriz de entrada de comprimento n ≥ 1, o tempo de execução do algoritmo DSelect é O (n).

Diferentemente do tempo de execução do algoritmo RSelect, que em princípio não pode ser maior que Θ (n2), o tempo de execução do algoritmo DSelect é sempre igual a O (n). No entanto, na prática, você deve preferir o RSelect ao algoritmo DSelect, porque o primeiro funciona no mesmo local, e a constante oculta no tempo médio de operação “O (n)” no Teorema 6.1 é menor que a constante oculta no Teorema 6.6.

»Mais informações sobre o livro podem ser encontradas no site do editor
» Conteúdo
» Trecho

Para Khabrozhiteley 20% de desconto no cupom - Algoritmos

Após o pagamento da versão em papel do livro, uma versão eletrônica do livro é enviada por e-mail.

PS: 7% do custo do livro será destinado à tradução de novos livros de informática; a lista de livros entregues à gráfica está aqui .