Entendendo o Q-learning, o problema “Andar sobre uma pedra”

Olá Habr! Trago à sua atenção uma tradução do artigo "Entendendo o Q-Learning, o problema da caminhada no penhasco", de Lucas Vazquez .

No último post, apresentamos o problema “Andar sobre uma pedra” e nos debruçamos sobre um algoritmo terrível que não fazia sentido. Desta vez, vamos revelar os segredos desta caixa cinza e ver que ela não é tão assustadora.

Sumário

Concluímos que, maximizando a quantidade de recompensas futuras, também encontramos o caminho mais rápido para a meta; portanto, nossa meta agora é encontrar uma maneira de fazer isso!

Introdução ao Q-Learning

• Vamos começar criando uma tabela que mede o desempenho de uma determinada ação em qualquer estado (podemos medi-la com um valor escalar simples; portanto, quanto maior o valor, melhor a ação)
• Esta tabela terá uma linha para cada estado e uma coluna para cada ação. Em nosso mundo, a grade possui 48 (4 por Y por 12 por X) estados e 4 ações são permitidas (cima, baixo, esquerda, direita), portanto a tabela será 48 x 4.
• Os valores armazenados nesta tabela são chamados de "valores Q".
• Essas são estimativas da quantidade de recompensas futuras. Em outras palavras, eles estimam quanto mais recompensas podemos obter antes do final do jogo, estando no estado S e realizando a ação A.
• Inicializamos a tabela com valores aleatórios (ou alguma constante, por exemplo, todos os zeros).

A “tabela Q” ideal possui valores que nos permitem realizar as melhores ações em cada estado, dando-nos a melhor maneira de vencer no final. O problema está resolvido, aplausos, Robot Lords :).

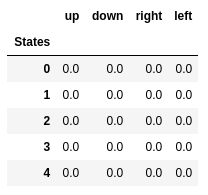Valores Q dos cinco primeiros estados.

Q-learning

• Q-learning é um algoritmo que "aprende" esses valores.
• A cada passo, obtemos mais informações sobre o mundo.
• Esta informação é usada para atualizar os valores na tabela.

Por exemplo, suponha que estamos a um passo do alvo (quadrado [2, 11]) e, se decidirmos descer, obteremos uma recompensa de 0 em vez de -1.
Podemos usar essas informações para atualizar o valor do par de ação de estado em nossa tabela e, na próxima vez em que o visitarmos, já saberemos que a descida nos dá uma recompensa de 0.

Agora podemos espalhar essas informações ainda mais! Como agora sabemos o caminho para o objetivo a partir do quadrado [2, 11], qualquer ação que nos leve ao quadrado [2, 11] também será boa, portanto atualizamos o valor Q do quadrado, o que nos leva a [2, 11] estar mais perto de 0.

E isso, senhoras e senhores, é a essência do Q-learning!

Observe que toda vez que atingimos a meta, aumentamos nosso "mapa" de como alcançá-la em um quadrado. Portanto, após um número suficiente de iterações, teremos um mapa completo que nos mostrará como chegar à meta de cada estado.

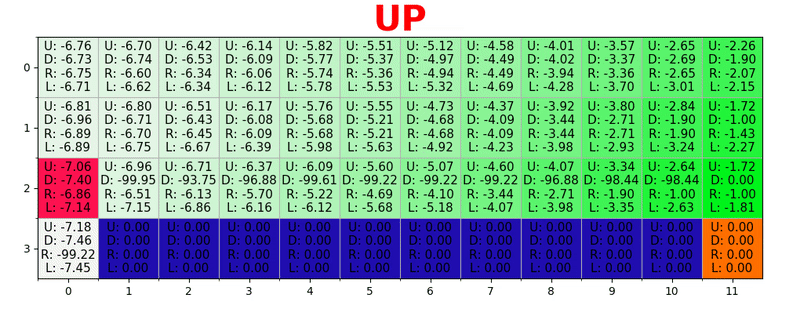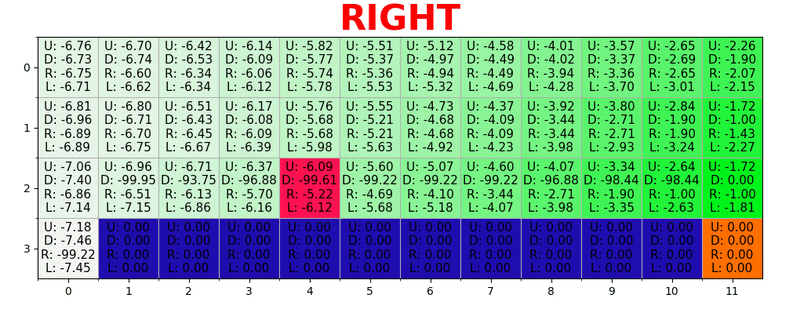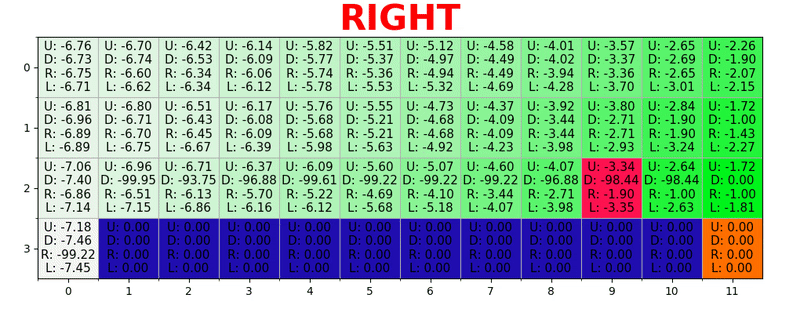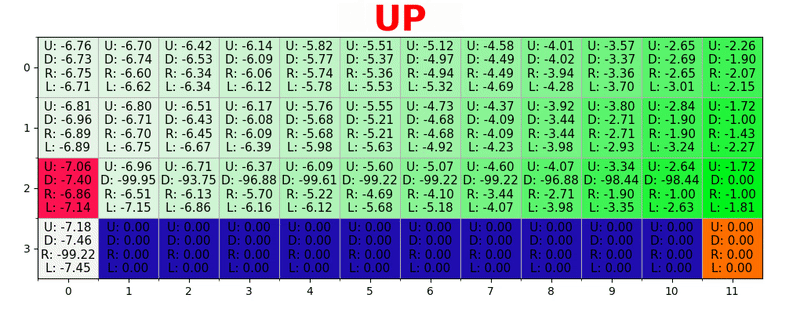Um caminho é gerado executando a melhor ação em todos os estados. Chave verde representa o significado de uma ação melhor, chaves mais saturadas representam um valor mais alto. O texto representa um valor para cada ação (cima, baixo, direita, esquerda).

Equação de Bellman

Antes de falarmos sobre código, vamos falar sobre matemática: o conceito básico de Q-learning, a equação de Bellman.

• Primeiro vamos esquecer γ nesta equação
• A equação afirma que o valor Q para um determinado par de ação e estado deve ser a recompensa recebida na transição para um novo estado (executando esta ação), adicionado ao valor da melhor ação no próximo estado.

Em outras palavras, divulgamos informações sobre os valores das ações, um passo de cada vez!

Mas podemos decidir que receber uma recompensa agora é mais valioso do que receber uma recompensa no futuro e, portanto, temos γ, um número de 0 a 1 (geralmente de 0,9 a 0,99) que é multiplicado por uma recompensa no futuro descontando recompensas futuras.

Portanto, dado γ = 0,9 e aplicando isso a alguns estados do nosso mundo (grade), temos:

Podemos comparar esses valores com os itens acima no GIF e ver se eles são iguais.

Implementação

Agora que temos um entendimento intuitivo de como o Q-learning funciona, podemos começar a pensar em implementar tudo isso, e usaremos o pseudocódigo do Q-learning do livro de Sutton como um guia.

Pseudocódigo do livro de Sutton.

Código:

# Initialize Q arbitrarily, in this case a table full of zeros q_values = np.zeros((num_states, num_actions)) # Iterate over 500 episodes for _ in range(500): state = env.reset() done = False # While episode is not over while not done: # Choose action action = egreedy_policy(q_values, state, epsilon=0.1) # Do the action next_state, reward, done = env.step(action) # Update q_values td_target = reward + gamma * np.max(q_values[next_state]) td_error = td_target - q_values[state][action] q_values[state][action] += learning_rate * td_error # Update state state = next_state 

• Primeiro, dizemos: “Para todos os estados e ações, inicializamos Q (s) a arbitrariamente”, isso significa que podemos criar nossa tabela de valores Q com quaisquer valores que desejamos, eles podem ser aleatórios, podem ser qualquer tipo de permanente não importa. Vemos que na linha 2 criamos uma tabela cheia de zeros.

Também dizemos: “O valor de Q para os estados finais é zero”, não podemos executar nenhuma ação nos estados finais; portanto, consideramos o valor de todas as ações nesse estado como zero.

• Para cada episódio, precisamos “inicializar S”, essa é apenas uma maneira elegante de dizer “reinicie o jogo”; no nosso caso, significa colocar o jogador na posição inicial; em nosso mundo, existe um método que faz exatamente isso, e o chamamos na linha 6.
• Para cada etapa do tempo (toda vez que precisamos agir), devemos escolher a ação obtida de Q.

Lembre-se, eu disse, “estamos tomando as ações que são mais valiosas em todas as condições?

Quando fazemos isso, usamos nossos valores Q para criar a política; nesse caso, será uma política gananciosa, porque sempre tomamos ações que, em nossa opinião, são as melhores em todos os estados; portanto, diz-se que agimos com avidez.

Lixo eletrônico

Mas há um problema com essa abordagem: imagine que estamos em um labirinto que possui duas recompensas, uma delas é +1 e a outra é +100 (e toda vez que encontramos uma delas, o jogo termina). Como sempre realizamos ações que consideramos as melhores, ficaremos presos ao primeiro prêmio encontrado, sempre retornando a ele; portanto, se reconhecermos primeiro o prêmio +1, perderemos o grande prêmio +100.

Solução

Precisamos garantir que estudemos o mundo o suficiente (essa é uma tarefa incrivelmente difícil). É aqui que ε entra em jogo. ε no algoritmo ganancioso significa que devemos agir ansiosamente, MAS executar ações aleatórias como uma porcentagem de ε ao longo do tempo, portanto, com um número infinito de tentativas, devemos examinar todos os estados.

A ação é selecionada de acordo com esta estratégia na linha 12, com epsilon = 0,1, o que significa que estamos pesquisando o mundo 10% do tempo. A implementação da política é a seguinte:

 def egreedy_policy(q_values, state, epsilon=0.1): # Get a random number from a uniform distribution between 0 and 1, # if the number is lower than epsilon choose a random action if np.random.random() < epsilon: return np.random.choice(4) # Else choose the action with the highest value else: return np.argmax(q_values[state]) 

Na linha 14 da primeira listagem, chamamos o método step para executar a ação, o mundo nos devolve o próximo estado, recompensa e informações sobre o final do jogo.

De volta à matemática:

Temos uma equação longa, vamos pensar sobre isso:

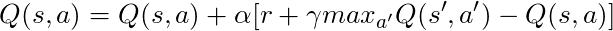
Se tomarmos α = 1:

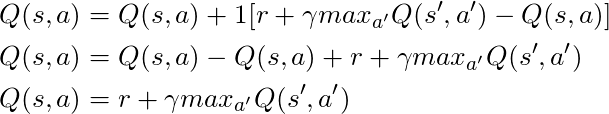
O que corresponde exatamente à equação de Bellman, que vimos alguns parágrafos atrás! Portanto, já sabemos que essa é a linha responsável pela disseminação de informações sobre os valores do estado.

Mas geralmente α (conhecido principalmente como velocidade de aprendizado) é muito menor que 1, seu objetivo principal é evitar grandes alterações em uma atualização; portanto, em vez de voar para o objetivo, abordamos-o lentamente. Em nossa abordagem tabular, definir α = 1 não causa problemas, mas ao trabalhar com redes neurais (mais sobre isso nos artigos a seguir), tudo pode facilmente sair do controle.

Observando o código, vemos que na linha 16 da primeira listagem que definimos td_target, esse é o valor que devemos aproximar, mas em vez de ir diretamente para esse valor na linha 17, calculamos td_error, usaremos esse valor em combinação com a velocidade aprendendo a avançar lentamente em direção à meta.

Lembre-se de que esta equação é uma entidade de Q-Learning.

Agora só precisamos atualizar nosso estado, e tudo está pronto, esta é a linha 20. Repetimos esse processo até chegarmos ao final do episódio, morrendo nas rochas ou atingindo a meta.

Conclusão

Agora, intuitivamente entendemos e sabemos como codificar o Q-Learning (pelo menos uma versão tabular), verifique todo o código usado para esta postagem, disponível no GitHub .

Visualização do teste do processo de aprendizagem:

Observe que todas as ações começam com um valor que excede seu valor final; esse é um truque para estimular a exploração do mundo.