Já discutimos o mecanismo de indexação do PostgreSQL e a interface dos métodos de acesso , bem como o índice de hash , um dos métodos de acesso. Vamos agora considerar a árvore B, o índice mais tradicional e amplamente usado. Este artigo é grande, portanto, seja paciente.

Btree

Estrutura

O tipo de índice B-tree, implementado como método de acesso "btree", é adequado para dados que podem ser classificados. Em outras palavras, os operadores "maior", "maior ou igual", "menor", "menor ou igual" e "igual" devem ser definidos para o tipo de dados. Observe que às vezes os mesmos dados podem ser classificados de maneira diferente, o que nos leva de volta ao conceito de família de operadores.

Como sempre, as linhas de índice da árvore B são compactadas em páginas. Nas páginas folha, essas linhas contêm dados a serem indexados (chaves) e referências a linhas da tabela (TIDs). Nas páginas internas, cada linha faz referência a uma página filha do índice e contém o valor mínimo nessa página.

As árvores B têm algumas características importantes:

• As árvores B são balanceadas, ou seja, cada página de folha é separada da raiz pelo mesmo número de páginas internas. Portanto, a pesquisa de qualquer valor leva o mesmo tempo.
  
• As árvores B são multi-ramificadas, ou seja, cada página (geralmente 8 KB) contém muitos TIDs (centenas). Como resultado, a profundidade das árvores B é bem pequena, na verdade, de 4 a 5 para tabelas muito grandes.
  
• Os dados no índice são classificados em ordem não decrescente (entre as páginas e dentro de cada página) e as páginas do mesmo nível são conectadas umas às outras por uma lista bidirecional. Portanto, podemos obter um conjunto de dados ordenados apenas por uma lista percorrendo uma ou outra direção sem retornar à raiz a cada vez.
  

Abaixo está um exemplo simplificado do índice em um campo com chaves inteiras.



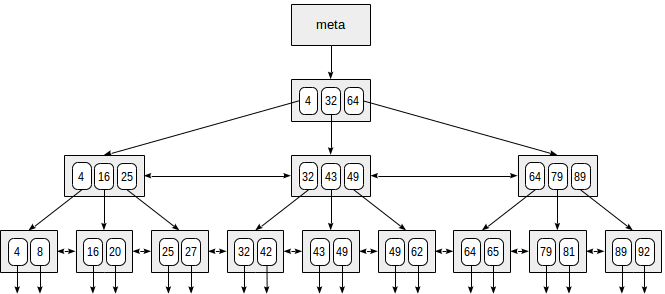
A primeira página do índice é uma metapágina, que faz referência à raiz do índice. Os nós internos estão localizados abaixo da raiz e as páginas folha estão na linha inferior. As setas para baixo representam referências de nós folha para linhas de tabela (TIDs).

Pesquisa por igualdade

Vamos considerar a pesquisa de um valor em uma árvore pela condição " indexed-field = expression ". Digamos, estamos interessados ​​na chave de 49.



A pesquisa começa com o nó raiz e precisamos determinar para qual dos nós filhos descer. Conhecendo as chaves no nó raiz (4, 32, 64), descobrimos, portanto, os intervalos de valores nos nós filhos. Desde 32 ≤ 49 <64, precisamos descer para o segundo nó filho. Em seguida, o mesmo processo é repetido recursivamente até chegarmos a um nó folha a partir do qual as TIDs necessárias podem ser obtidas.

Na realidade, vários detalhes complicam esse processo aparentemente simples. Por exemplo, um índice pode conter chaves não exclusivas e pode haver tantos valores iguais que eles não cabem em uma página. Voltando ao nosso exemplo, parece que deveríamos descer do nó interno sobre a referência ao valor de 49. Mas, como mostra a figura, dessa forma, pularemos uma das teclas "49" na folha anterior . Portanto, uma vez que encontramos uma chave exatamente igual em uma página interna, precisamos descer uma posição para a esquerda e, em seguida, examinar as linhas de índice do nível subjacente da esquerda para a direita em busca da chave procurada.

(Outra complicação é que, durante a pesquisa, outros processos podem alterar os dados: a árvore pode ser reconstruída, as páginas podem ser divididas em duas etc. Todos os algoritmos são projetados para que essas operações simultâneas não interfiram entre si e não causem bloqueios extras sempre que possível. Mas evitaremos expandir isso.)

Pesquisa por desigualdade

Ao pesquisar pela condição " campo indexado ≤ expressão " (ou " campo indexado ≥ expressão "), primeiro encontramos um valor (se houver) no índice pela condição de igualdade " campo indexado = expressão " e depois percorremos páginas da folha na direção apropriada até o fim.

A figura ilustra esse processo para n ≤ 35:



Os operadores "maior" e "menos" são suportados de maneira semelhante, exceto que o valor encontrado inicialmente deve ser descartado.

Pesquisa por faixa

Ao pesquisar pelo intervalo " expressão1 ≤ campo indexado ≤ expressão2 ", encontramos um valor pela condição " campo indexado = expressão1 " e continuamos percorrendo as páginas das folhas enquanto a condição " campo indexado ≤ expressão2 " é atendida; ou vice-versa: comece com a segunda expressão e caminhe em uma direção oposta até alcançarmos a primeira expressão.

A figura mostra esse processo para a condição 23 ≤ n ≤ 64:

Exemplo

Vejamos um exemplo de como são os planos de consulta. Como sempre, usamos o banco de dados de demonstração e, desta vez, consideraremos a tabela da aeronave. Ele contém apenas nove linhas e o planejador optaria por não usar o índice, pois a tabela inteira cabe uma página. Mas esta tabela é interessante para nós com um propósito ilustrativo.

demo=# select * from aircrafts; 

  aircraft_code | model | range ---------------+---------------------+------- 773 | Boeing 777-300 | 11100 763 | Boeing 767-300 | 7900 SU9 | Sukhoi SuperJet-100 | 3000 320 | Airbus A320-200 | 5700 321 | Airbus A321-200 | 5600 319 | Airbus A319-100 | 6700 733 | Boeing 737-300 | 4200 CN1 | Cessna 208 Caravan | 1200 CR2 | Bombardier CRJ-200 | 2700 (9 rows) 

 demo=# create index on aircrafts(range); demo=# set enable_seqscan = off; 

(Ou explicitamente, "crie índice em aeronaves usando btree (range)", mas é uma árvore B criada por padrão.)

Pesquisa por igualdade:

 demo=# explain(costs off) select * from aircrafts where range = 3000; 

  QUERY PLAN --------------------------------------------------- Index Scan using aircrafts_range_idx on aircrafts Index Cond: (range = 3000) (2 rows) 

Pesquisa por desigualdade:

 demo=# explain(costs off) select * from aircrafts where range < 3000; 

  QUERY PLAN --------------------------------------------------- Index Scan using aircrafts_range_idx on aircrafts Index Cond: (range < 3000) (2 rows) 

E por faixa:

 demo=# explain(costs off) select * from aircrafts where range between 3000 and 5000; 

  QUERY PLAN ----------------------------------------------------- Index Scan using aircrafts_range_idx on aircrafts Index Cond: ((range >= 3000) AND (range <= 5000)) (2 rows) 

Classificação

Vamos enfatizar novamente que, com qualquer tipo de verificação (índice, somente índice ou bitmap), o método de acesso "btree" retorna dados ordenados, que podemos ver claramente nas figuras acima.

Portanto, se uma tabela tiver um índice na condição de classificação, o otimizador considerará as duas opções: varredura de índice da tabela, que retorna prontamente os dados classificados e varredura seqüencial da tabela com a classificação subsequente do resultado.

Ordem de classificação

Ao criar um índice, podemos especificar explicitamente a ordem de classificação. Por exemplo, podemos criar um índice por faixas de vôo desta maneira em particular:

 demo=# create index on aircrafts(range desc); 

Nesse caso, valores maiores apareceriam na árvore à esquerda, enquanto valores menores apareceriam à direita. Por que isso pode ser necessário se podemos percorrer os valores indexados em qualquer direção?

O objetivo é índices com várias colunas. Vamos criar uma exibição para mostrar modelos de aeronaves com uma divisão convencional em embarcações de curto, médio e longo alcance:

 demo=# create view aircrafts_v as select model, case when range < 4000 then 1 when range < 10000 then 2 else 3 end as class from aircrafts; demo=# select * from aircrafts_v; 

  model | class ---------------------+------- Boeing 777-300 | 3 Boeing 767-300 | 2 Sukhoi SuperJet-100 | 1 Airbus A320-200 | 2 Airbus A321-200 | 2 Airbus A319-100 | 2 Boeing 737-300 | 2 Cessna 208 Caravan | 1 Bombardier CRJ-200 | 1 (9 rows) 

E vamos criar um índice (usando a expressão):

 demo=# create index on aircrafts( (case when range < 4000 then 1 when range < 10000 then 2 else 3 end), model); 

Agora podemos usar esse índice para obter dados classificados por ambas as colunas em ordem crescente:

 demo=# select class, model from aircrafts_v order by class, model; 

  class | model -------+--------------------- 1 | Bombardier CRJ-200 1 | Cessna 208 Caravan 1 | Sukhoi SuperJet-100 2 | Airbus A319-100 2 | Airbus A320-200 2 | Airbus A321-200 2 | Boeing 737-300 2 | Boeing 767-300 3 | Boeing 777-300 (9 rows) 

 demo=# explain(costs off) select class, model from aircrafts_v order by class, model; 

  QUERY PLAN -------------------------------------------------------- Index Scan using aircrafts_case_model_idx on aircrafts (1 row) 

Da mesma forma, podemos executar a consulta para classificar os dados em ordem decrescente:

 demo=# select class, model from aircrafts_v order by class desc, model desc; 

  class | model -------+--------------------- 3 | Boeing 777-300 2 | Boeing 767-300 2 | Boeing 737-300 2 | Airbus A321-200 2 | Airbus A320-200 2 | Airbus A319-100 1 | Sukhoi SuperJet-100 1 | Cessna 208 Caravan 1 | Bombardier CRJ-200 (9 rows) 

 demo=# explain(costs off) select class, model from aircrafts_v order by class desc, model desc; 

  QUERY PLAN ----------------------------------------------------------------- Index Scan BACKWARD using aircrafts_case_model_idx on aircrafts (1 row) 

No entanto, não podemos usar esse índice para obter dados classificados por uma coluna em ordem decrescente e pela outra coluna em ordem crescente. Isso exigirá classificação separadamente:

 demo=# explain(costs off) select class, model from aircrafts_v order by class ASC, model DESC; 

  QUERY PLAN ------------------------------------------------- Sort Sort Key: (CASE ... END), aircrafts.model DESC -> Seq Scan on aircrafts (3 rows) 

(Observe que, como último recurso, o planejador escolheu a varredura sequencial, independentemente da configuração "enable_seqscan = off" feita anteriormente. Isso ocorre porque, na verdade, essa configuração não proíbe a varredura de tabela, mas apenas define seu custo astronômico - consulte o plano com "Custos".)

Para fazer essa consulta usar o índice, o último deve ser criado com a direção de classificação necessária:

 demo=# create index aircrafts_case_asc_model_desc_idx on aircrafts( (case when range < 4000 then 1 when range < 10000 then 2 else 3 end) ASC, model DESC); demo=# explain(costs off) select class, model from aircrafts_v order by class ASC, model DESC; 

  QUERY PLAN ----------------------------------------------------------------- Index Scan using aircrafts_case_asc_model_desc_idx on aircrafts (1 row) 

Ordem das colunas

Outro problema que surge ao usar índices de várias colunas é a ordem de listar colunas em um índice. Para a árvore B, essa ordem é de enorme importância: os dados dentro das páginas serão classificados pelo primeiro campo, depois pelo segundo e assim por diante.

Podemos representar o índice que construímos em intervalos e modelos de intervalo de maneira simbólica, da seguinte maneira:



Na verdade, um índice tão pequeno certamente caberá em uma página raiz. Na figura, ele é deliberadamente distribuído entre várias páginas para maior clareza.

Está claro neste gráfico que a pesquisa por predicados como "class = 3" (pesquisa apenas no primeiro campo) ou "class = 3 e model = 'Boeing 777-300'" (pesquisa nos dois campos) funcionará com eficiência.

No entanto, a pesquisa pelo predicado “model = 'Boeing 777-300'” será muito menos eficiente: começando pela raiz, não podemos determinar para qual nó filho descer, portanto, teremos que descer para todos eles. Isso não significa que um índice como esse nunca possa ser usado - sua eficiência está em questão. Por exemplo, se tivéssemos três classes de aeronaves e muitos modelos em cada classe, teríamos que examinar cerca de um terço do índice e isso poderia ter sido mais eficiente do que a verificação completa da tabela ... ou não.

No entanto, se criarmos um índice como este:

 demo=# create index on aircrafts( model, (case when range < 4000 then 1 when range < 10000 then 2 else 3 end)); 

a ordem dos campos será alterada:



Com esse índice, a pesquisa pelo predicado "model = 'Boeing 777-300'" funcionará eficientemente, mas a pesquisa pelo predicado "class = 3" não funcionará.

Nulos

O método de acesso "Btree" indexa NULLs e suporta a pesquisa por condições É NULL e NÃO É NULL.

Vamos considerar a tabela de vôos, onde ocorrem NULLs:

 demo=# create index on flights(actual_arrival); demo=# explain(costs off) select * from flights where actual_arrival is null; 

  QUERY PLAN ------------------------------------------------------- Bitmap Heap Scan on flights Recheck Cond: (actual_arrival IS NULL) -> Bitmap Index Scan on flights_actual_arrival_idx Index Cond: (actual_arrival IS NULL) (4 rows) 

NULLs estão localizados em uma ou na outra extremidade dos nós folha, dependendo de como o índice foi criado (NULLS FIRST ou NULLS LAST). Isso é importante se uma consulta incluir classificação: o índice poderá ser usado se o comando SELECT especificar a mesma ordem de NULLs na sua cláusula ORDER BY que a ordem especificada para o índice criado (NULLS FIRST ou NULLS LAST).

No exemplo a seguir, esses pedidos são os mesmos, portanto, podemos usar o índice:

 demo=# explain(costs off) select * from flights order by actual_arrival NULLS LAST; 

  QUERY PLAN -------------------------------------------------------- Index Scan using flights_actual_arrival_idx on flights (1 row) 

E aqui esses pedidos são diferentes, e o otimizador escolhe a varredura seqüencial com a classificação subsequente:

 demo=# explain(costs off) select * from flights order by actual_arrival NULLS FIRST; 

  QUERY PLAN ---------------------------------------- Sort Sort Key: actual_arrival NULLS FIRST -> Seq Scan on flights (3 rows) 

Para usar o índice, ele deve ser criado com NULLs localizados no início:

 demo=# create index flights_nulls_first_idx on flights(actual_arrival NULLS FIRST); demo=# explain(costs off) select * from flights order by actual_arrival NULLS FIRST; 

  QUERY PLAN ----------------------------------------------------- Index Scan using flights_nulls_first_idx on flights (1 row) 

Problemas como esse certamente são causados ​​por NULLs não serem classificados, ou seja, o resultado da comparação de NULL e qualquer outro valor é indefinido:

 demo=# \pset null NULL demo=# select null < 42; 

  ?column? ---------- NULL (1 row) 

Isso contraria o conceito de árvore B e não se encaixa no padrão geral. Os NULLs, no entanto, desempenham um papel tão importante nos bancos de dados que sempre precisamos abrir exceções para eles.

Como os NULLs podem ser indexados, é possível usar um índice mesmo sem as condições impostas à tabela (já que o índice contém informações sobre todas as linhas da tabela). Isso pode fazer sentido se a consulta exigir ordem de dados e o índice garantir a ordem necessária. Nesse caso, o planejador pode escolher o acesso ao índice para salvar em uma classificação separada.

Propriedades

Vamos examinar as propriedades do método de acesso "btree" (as consultas já foram fornecidas ).

  amname | name | pg_indexam_has_property --------+---------------+------------------------- btree | can_order | t btree | can_unique | t btree | can_multi_col | t btree | can_exclude | t 

Como vimos, o B-tree pode solicitar dados e suporta exclusividade - e este é o único método de acesso que nos fornece propriedades como essas. Os índices de várias colunas também são permitidos, mas outros métodos de acesso (embora nem todos eles) também possam suportar esses índices. Discutiremos o suporte à restrição EXCLUDE da próxima vez, e não sem razão.

  name | pg_index_has_property ---------------+----------------------- clusterable | t index_scan | t bitmap_scan | t backward_scan | t 

O método de acesso "Btree" suporta as duas técnicas para obter valores: verificação de índice, bem como verificação de bitmap. E como pudemos ver, o método de acesso pode percorrer a árvore "para frente" e "para trás".

  name | pg_index_column_has_property --------------------+------------------------------ asc | t desc | f nulls_first | f nulls_last | t orderable | t distance_orderable | f returnable | t search_array | t search_nulls | t 

As primeiras quatro propriedades dessa camada explicam como exatamente os valores de uma determinada coluna específica são ordenados. Neste exemplo, os valores são classificados em ordem crescente ("asc") e os NULLs são fornecidos por último ("nulls_last"). Mas, como já vimos, outras combinações são possíveis.

A propriedade "Search_array" indica suporte para expressões como esta pelo índice:

 demo=# explain(costs off) select * from aircrafts where aircraft_code in ('733','763','773'); 

  QUERY PLAN ----------------------------------------------------------------- Index Scan using aircrafts_pkey on aircrafts Index Cond: (aircraft_code = ANY ('{733,763,773}'::bpchar[])) (2 rows) 

A propriedade "Retornável" indica suporte à varredura apenas de índice, o que é razoável, pois as linhas do índice armazenam os valores indexados (diferentemente do índice de hash, por exemplo). Aqui faz sentido dizer algumas palavras sobre a cobertura de índices baseados em árvore B.

Índices exclusivos com linhas adicionais

Como discutimos anteriormente , um índice de cobertura é aquele que armazena todos os valores necessários para uma consulta, não sendo necessário o acesso à própria tabela (quase). Um índice exclusivo pode ser especificamente coberto.

Mas vamos assumir que queremos adicionar colunas extras necessárias para uma consulta ao índice exclusivo. No entanto, a exclusividade de tais valores compostos não garante a exclusividade da chave e serão necessários dois índices nas mesmas colunas: um exclusivo para suportar a restrição de integridade e outro para ser usado como cobertura. Isso é ineficiente, com certeza.

Em nossa empresa, a Anastasiya Lubennikova lubennikovaav aprimorou o método "btree" para que colunas adicionais, não exclusivas, pudessem ser incluídas em um índice exclusivo. Esperamos que esse patch seja adotado pela comunidade para se tornar parte do PostgreSQL, mas isso não acontecerá tão cedo quanto na versão 10. Neste momento, o patch está disponível no Pro Standard 9.5+ e é isso que parece gosto.

De fato, este patch foi confirmado no PostgreSQL 11.

Vamos considerar a tabela de reservas:

 demo=# \d bookings 

  Table "bookings.bookings" Column | Type | Modifiers --------------+--------------------------+----------- book_ref | character(6) | not null book_date | timestamp with time zone | not null total_amount | numeric(10,2) | not null Indexes: "bookings_pkey" PRIMARY KEY, btree (book_ref) Referenced by: TABLE "tickets" CONSTRAINT "tickets_book_ref_fkey" FOREIGN KEY (book_ref) REFERENCES bookings(book_ref) 

Nesta tabela, a chave primária (book_ref, código de reserva) é fornecida por um índice "btree" regular. Vamos criar um novo índice exclusivo com uma coluna adicional:

 demo=# create unique index bookings_pkey2 on bookings(book_ref) INCLUDE (book_date); 

Agora substituímos o índice existente por um novo (na transação, para aplicar todas as alterações simultaneamente):

 demo=# begin; demo=# alter table bookings drop constraint bookings_pkey cascade; demo=# alter table bookings add primary key using index bookings_pkey2; demo=# alter table tickets add foreign key (book_ref) references bookings (book_ref); demo=# commit; 

Isto é o que obtemos:

 demo=# \d bookings 

  Table "bookings.bookings" Column | Type | Modifiers --------------+--------------------------+----------- book_ref | character(6) | not null book_date | timestamp with time zone | not null total_amount | numeric(10,2) | not null Indexes: "bookings_pkey2" PRIMARY KEY, btree (book_ref) INCLUDE (book_date) Referenced by: TABLE "tickets" CONSTRAINT "tickets_book_ref_fkey" FOREIGN KEY (book_ref) REFERENCES bookings(book_ref) 

Agora, um e o mesmo índice funciona como exclusivo e serve como um índice de cobertura para esta consulta, por exemplo:

 demo=# explain(costs off) select book_ref, book_date from bookings where book_ref = '059FC4'; 

  QUERY PLAN -------------------------------------------------- Index Only Scan using bookings_pkey2 on bookings Index Cond: (book_ref = '059FC4'::bpchar) (2 rows) 

Criação do índice

É sabido, mas não menos importante, que, para uma tabela de tamanho grande, é melhor carregar dados sem índices e criar os índices necessários posteriormente. Isso não é apenas mais rápido, mas provavelmente o índice terá um tamanho menor.

O fato é que a criação do índice "btree" usa um processo mais eficiente do que a inserção de valores por linha na árvore. Aproximadamente, todos os dados disponíveis na tabela são classificados e as páginas em folha desses dados são criadas. As páginas internas são "construídas sobre" essa base até que toda a pirâmide converja para a raiz.

A velocidade desse processo depende do tamanho da RAM disponível, limitada pelo parâmetro "maintenance_work_mem". Portanto, aumentar o valor do parâmetro pode acelerar o processo. Para índices exclusivos, a memória do tamanho "work_mem" é alocada além de "maintenance_work_mem".

Semântica de comparação

A última vez que mencionamos que o PostgreSQL precisa saber quais funções hash exigem valores de tipos diferentes e que essa associação é armazenada no método de acesso "hash". Da mesma forma, o sistema deve descobrir como ordenar valores. Isso é necessário para classificações, agrupamentos (algumas vezes), junções de mesclagem e assim por diante. O PostgreSQL não se liga a nomes de operadores (como>, <, =), pois os usuários podem definir seu próprio tipo de dados e atribuir nomes diferentes aos operadores correspondentes. Uma família de operadores usada pelo método de acesso "btree" define os nomes dos operadores.

Por exemplo, esses operadores de comparação são usados ​​na família de operadores "bool_ops":

 postgres=# select amop.amopopr::regoperator as opfamily_operator, amop.amopstrategy from pg_am am, pg_opfamily opf, pg_amop amop where opf.opfmethod = am.oid and amop.amopfamily = opf.oid and am.amname = 'btree' and opf.opfname = 'bool_ops' order by amopstrategy; 

  opfamily_operator | amopstrategy ---------------------+-------------- <(boolean,boolean) | 1 <=(boolean,boolean) | 2 =(boolean,boolean) | 3 >=(boolean,boolean) | 4 >(boolean,boolean) | 5 (5 rows) 

Aqui podemos ver cinco operadores de comparação, mas como já mencionado, não devemos confiar em seus nomes. Para descobrir qual comparação cada operador faz, o conceito de estratégia é introduzido. Cinco estratégias são definidas para descrever a semântica do operador:

• 1 - menos
• 2 - menor ou igual
• 3 - igual
• 4 - maior ou igual
• 5 - maior

Algumas famílias de operadores podem conter vários operadores que implementam uma estratégia. Por exemplo, a família de operadores "integer_ops" contém os seguintes operadores para a estratégia 1:

 postgres=# select amop.amopopr::regoperator as opfamily_operator from pg_am am, pg_opfamily opf, pg_amop amop where opf.opfmethod = am.oid and amop.amopfamily = opf.oid and am.amname = 'btree' and opf.opfname = 'integer_ops' and amop.amopstrategy = 1 order by opfamily_operator; 

  opfamily_operator ---------------------- <(integer,bigint) <(smallint,smallint) <(integer,integer) <(bigint,bigint) <(bigint,integer) <(smallint,integer) <(integer,smallint) <(smallint,bigint) <(bigint,smallint) (9 rows) 

Graças a isso, o otimizador pode evitar a conversão de tipos ao comparar valores de diferentes tipos contidos em uma família de operadores.

Suporte de índice para um novo tipo de dados

A documentação fornece um exemplo de criação de um novo tipo de dados para números complexos e de uma classe de operador para classificar valores desse tipo. Este exemplo usa a linguagem C, que é absolutamente razoável quando a velocidade é crítica. Mas nada nos impede de usar SQL puro para o mesmo experimento, apenas para tentar entender melhor a semântica da comparação.

Vamos criar um novo tipo composto com dois campos: partes reais e imaginárias.

 postgres=# create type complex as (re float, im float); 

Podemos criar uma tabela com um campo do novo tipo e adicionar alguns valores à tabela:

 postgres=# create table numbers(x complex); postgres=# insert into numbers values ((0.0, 10.0)), ((1.0, 3.0)), ((1.0, 1.0)); 

Agora surge uma pergunta: como ordenar números complexos se nenhuma relação de ordem é definida para eles no sentido matemático?

Como se vê, os operadores de comparação já estão definidos para nós:

 postgres=# select * from numbers order by x; 

  x -------- (0,10) (1,1) (1,3) (3 rows) 

Por padrão, a classificação é componente por componente para um tipo composto: os primeiros campos são comparados, os segundos campos e assim por diante, aproximadamente da mesma maneira que as seqüências de texto são comparadas caractere por caractere. Mas podemos definir uma ordem diferente. Por exemplo, números complexos podem ser tratados como vetores e ordenados pelo módulo (comprimento), que é calculado como a raiz quadrada da soma dos quadrados das coordenadas (o teorema de Pitágoras). Para definir essa ordem, vamos criar uma função auxiliar que calcula o módulo:

 postgres=# create function modulus(a complex) returns float as $$ select sqrt(a.re*a.re + a.im*a.im); $$ immutable language sql; 

Agora definiremos sistematicamente funções para todos os cinco operadores de comparação usando esta função auxiliar:

 postgres=# create function complex_lt(a complex, b complex) returns boolean as $$ select modulus(a) < modulus(b); $$ immutable language sql; postgres=# create function complex_le(a complex, b complex) returns boolean as $$ select modulus(a) <= modulus(b); $$ immutable language sql; postgres=# create function complex_eq(a complex, b complex) returns boolean as $$ select modulus(a) = modulus(b); $$ immutable language sql; postgres=# create function complex_ge(a complex, b complex) returns boolean as $$ select modulus(a) >= modulus(b); $$ immutable language sql; postgres=# create function complex_gt(a complex, b complex) returns boolean as $$ select modulus(a) > modulus(b); $$ immutable language sql; 

E criaremos operadores correspondentes. Para ilustrar que eles não precisam ser chamados ">", "<" e assim por diante, vamos dar a eles nomes "estranhos".

 postgres=# create operator #<#(leftarg=complex, rightarg=complex, procedure=complex_lt); postgres=# create operator #<=#(leftarg=complex, rightarg=complex, procedure=complex_le); postgres=# create operator #=#(leftarg=complex, rightarg=complex, procedure=complex_eq); postgres=# create operator #>=#(leftarg=complex, rightarg=complex, procedure=complex_ge); postgres=# create operator #>#(leftarg=complex, rightarg=complex, procedure=complex_gt); 

Neste ponto, podemos comparar números:

 postgres=# select (1.0,1.0)::complex #<# (1.0,3.0)::complex; 

  ?column? ---------- t (1 row) 

Além de cinco operadores, o método de acesso "btree" exige que mais uma função (excessiva, mas conveniente) seja definida: ele deve retornar -1, 0 ou 1 se o primeiro valor for menor que, igual a ou maior que o segundo um. Essa função auxiliar é chamada de suporte. Outros métodos de acesso podem exigir a definição de outras funções de suporte.

 postgres=# create function complex_cmp(a complex, b complex) returns integer as $$ select case when modulus(a) < modulus(b) then -1 when modulus(a) > modulus(b) then 1 else 0 end; $$ language sql; 

Agora estamos prontos para criar uma classe de operadores (e a família de operadores com o mesmo nome será criada automaticamente):

 postgres=# create operator class complex_ops default for type complex using btree as operator 1 #<#, operator 2 #<=#, operator 3 #=#, operator 4 #>=#, operator 5 #>#, function 1 complex_cmp(complex,complex); 

Agora a classificação funciona como desejado:

 postgres=# select * from numbers order by x; 

  x -------- (1,1) (1,3) (0,10) (3 rows) 

E certamente será suportado pelo índice "btree".

Para concluir a imagem, você pode obter funções de suporte usando esta consulta:

 postgres=# select amp.amprocnum, amp.amproc, amp.amproclefttype::regtype, amp.amprocrighttype::regtype from pg_opfamily opf, pg_am am, pg_amproc amp where opf.opfname = 'complex_ops' and opf.opfmethod = am.oid and am.amname = 'btree' and amp.amprocfamily = opf.oid; 

  amprocnum | amproc | amproclefttype | amprocrighttype -----------+-------------+----------------+----------------- 1 | complex_cmp | complex | complex (1 row) 

Internals

Podemos explorar a estrutura interna do B-tree usando a extensão "pageinspect".

 demo=# create extension pageinspect; 

Metapagem do índice:

 demo=# select * from bt_metap('ticket_flights_pkey'); 

  magic | version | root | level | fastroot | fastlevel --------+---------+------+-------+----------+----------- 340322 | 2 | 164 | 2 | 164 | 2 (1 row) 

O mais interessante aqui é o nível do índice: o índice em duas colunas para uma tabela com um milhão de linhas, exigindo apenas dois níveis (não incluindo a raiz).

Informação estatística no bloco 164 (raiz):

 demo=# select type, live_items, dead_items, avg_item_size, page_size, free_size from bt_page_stats('ticket_flights_pkey',164); 

  type | live_items | dead_items | avg_item_size | page_size | free_size ------+------------+------------+---------------+-----------+----------- r | 33 | 0 | 31 | 8192 | 6984 (1 row) 

E os dados no bloco (o campo "dados", que é sacrificado aqui para a largura da tela, contém o valor da chave de indexação na representação binária):

 demo=# select itemoffset, ctid, itemlen, left(data,56) as data from bt_page_items('ticket_flights_pkey',164) limit 5; 

  itemoffset | ctid | itemlen | data ------------+---------+---------+---------------------------------------------------------- 1 | (3,1) | 8 | 2 | (163,1) | 32 | 1d 30 30 30 35 34 33 32 33 30 35 37 37 31 00 00 ff 5f 00 3 | (323,1) | 32 | 1d 30 30 30 35 34 33 32 34 32 33 36 36 32 00 00 4f 78 00 4 | (482,1) | 32 | 1d 30 30 30 35 34 33 32 35 33 30 38 39 33 00 00 4d 1e 00 5 | (641,1) | 32 | 1d 30 30 30 35 34 33 32 36 35 35 37 38 35 00 00 2b 09 00 (5 rows) 

O primeiro elemento refere-se a técnicas e especifica o limite superior de todos os elementos no bloco (um detalhe de implementação que não discutimos), enquanto os dados em si começam com o segundo elemento. É claro que o nó filho mais à esquerda é o bloco 163, seguido pelo bloco 323 e assim por diante. Eles, por sua vez, podem ser explorados usando as mesmas funções.

Agora, seguindo uma boa tradição, faz sentido ler a documentação, o README e o código-fonte.

Ainda mais uma extensão potencialmente útil é o " amcheck ", que será incorporado no PostgreSQL 10, e para versões inferiores, você pode obtê-lo no github . Essa extensão verifica a consistência lógica dos dados nas árvores B e nos permite detectar falhas com antecedência.

Isso é verdade, "amcheck" faz parte do PostgreSQL a partir da versão 10.

Continue lendo .