Finalmente, um guia em russo para o idioma Julia apareceu. Ele fornece uma introdução completa à linguagem para aqueles que têm pouca experiência em programação (o restante será útil para o desenvolvimento geral), há também uma introdução ao aprendizado de máquina e várias tarefas para consolidar o material.
Durante a pesquisa, deparei-me com um curso de programação para economistas (além de Julia, também há Python). Os experientes podem fazer um curso rápido ou ler o livro Como pensar como um cientista da computação
A seguir, uma tradução do material do blog Christopher Rackauckas 7 Julia Gotchas e como lidar com eles
Deixe-me começar dizendo que Julia é uma linguagem maravilhosa. Eu a amo, é isso que considero a linguagem mais poderosa e intuitiva que já usei. Este é sem dúvida o meu idioma favorito. No entanto, existem algumas "armadilhas", pequenas coisas complicadas que você precisa saber. Cada idioma os possui, e uma das primeiras coisas que você deve fazer para dominar o idioma é descobrir o que são e como evitá-los. O objetivo desta publicação é ajudá-lo a acelerar esse processo, expondo alguns dos
Julia é uma boa linguagem para entender o que está acontecendo, porque não há mágica nela. Os desenvolvedores de Julia queriam ter regras de conduta claramente definidas. Isso significa que todo comportamento pode ser explicado. No entanto, isso pode significar que você precisa esforçar a cabeça para entender por que isso e não o outro estão acontecendo. É por isso que não vou apenas explicar alguns problemas comuns, mas também vou explicar por que eles surgem. Você verá que existem alguns padrões muito semelhantes e, uma vez que você se conscientiza deles, não se diverte mais com nenhum deles. Por esse motivo, Julia possui uma curva de aprendizado um pouco mais íngreme em comparação com linguagens mais simples, como MATLAB / R / Python . No entanto, depois de dominar isso, você poderá usar totalmente o laconicismo de Julia para obter o desempenho do C / Fortran . Agora vá mais fundo.
Inesperadamente: REPL (terminal) tem um escopo global
Esse é de longe o problema mais comum relatado pelos novos usuários de Julia. Alguém dirá: “Ouvi dizer que Julia é rápida!”, Abra o REPL, anote rapidamente algum algoritmo conhecido e execute esse script. Após sua execução, eles olham para o tempo e dizem: “Espere um segundo, por que é lento, como no Python?” Como esse é um problema tão importante e comum, vamos dedicar algum tempo a explorar as razões pelas quais isso acontece para descobrir como evitar isso.
Uma pequena digressão: por que Julia é rápida
Você deve entender que Julia não é apenas uma compilação de código, mas também uma especialização de tipos (ou seja, compilação de código que é específica para esses tipos). Deixe-me reiterar: Julia não é rápida, porque o código é compilado usando o compilador JIT, mas o segredo da velocidade é que o código específico do tipo é compilado.
Se você precisar de uma história completa, confira algumas das anotações que escrevi para o próximo seminário . A especificidade do tipo é determinada pelo princípio básico do design de Julia: despacho múltiplo . Quando você escreve o código:
function f(a,b) return 2a+b end
Parece que essa é apenas uma f(2.0,3.0) , Julia executará o código compilado, que pega dois números de ponto flutuante e retorna 2a + b . Se você chamar f(2,3) , Julia executará outro código compilado que usa dois números inteiros e retorna 2a + b . A função f é uma abstração ou abreviação para muitos métodos diferentes que têm a mesma forma, e esse esquema de usar o símbolo f para chamar todos esses métodos diferentes é chamado de despacho múltiplo. E isso se aplica a todos os lugares: o operador + é na verdade uma função que chamará métodos, dependendo dos tipos que vê. Julia realmente obtém sua velocidade porque o código compilado conhece seus tipos e, portanto, o código compilado que chama f (2.0,3.0) é exatamente o código compilado que você obtém definindo a mesma função no C / Fortran . Você pode verificar isso com a macro code_native para ver o assembly compilado:
@code_native f(2.0,3.0)
pushq %rbp movq %rsp, %rbp Source line: 2 vaddsd %xmm0, %xmm0, %xmm0 vaddsd %xmm1, %xmm0, %xmm0 popq %rbp retq nop
Este é o mesmo assembly compilado que você espera de uma função no C / Fortran e difere do código do assembly para números inteiros:
@code_native f(2,3) pushq %rbp movq %rsp, %rbp Source line: 2 leaq (%rdx,%rcx,2), %rax popq %rbp retq nopw (%rax,%rax)
Essência: REPL / Global Scope não permite especificidade de tipo
Isso nos leva ao ponto principal: o REPL / Global Scope é lento porque não permite a especificação de tipos. Antes de tudo, observe que o REPL é um escopo global porque Julia permite escopo aninhado para funções. Por exemplo, se definirmos
function outer() a = 5 function inner() return 2a end b = inner() return 3a+b end
veremos que esse código funciona. Isso ocorre porque Julia permite capturar
a=2.0; b=3.0 function linearcombo() return 2a+b end ans = linearcombo()
e
a = 2; b = 3 ans2= linearcombo()
Pergunta: Quais tipos o compilador deve aceitar para a e b ? Observe que neste exemplo, alteramos os tipos e ainda chamamos a mesma função. Ele pode lidar com quaisquer tipos que adicionamos a ele: flutuante, números inteiros, matrizes, tipos de usuários estranhos etc. Na linguagem Julia, isso significa que as variáveis devem ser encaixotadas e os tipos são verificados toda vez que são usados. Como você acha que o código compilado se parece?
Volumoso pushq %rbp movq %rsp, %rbp pushq %r15 pushq %r14 pushq %r12 pushq %rsi pushq %rdi pushq %rbx subq $96, %rsp movl $2147565792, %edi # imm = 0x800140E0 movabsq $jl_get_ptls_states, %rax callq *%rax movq %rax, %rsi leaq -72(%rbp), %r14 movq $0, -88(%rbp) vxorps %xmm0, %xmm0, %xmm0 vmovups %xmm0, -72(%rbp) movq $0, -56(%rbp) movq $10, -104(%rbp) movq (%rsi), %rax movq %rax, -96(%rbp) leaq -104(%rbp), %rax movq %rax, (%rsi) Source line: 3 movq pcre2_default_compile_context_8(%rdi), %rax movq %rax, -56(%rbp) movl $2154391480, %eax # imm = 0x806967B8 vmovq %rax, %xmm0 vpslldq $8, %xmm0, %xmm0 # xmm0 = zero,zero,zero,zero,zero,zero,zero,zero,xmm0[0,1,2,3,4,5,6,7] vmovdqu %xmm0, -80(%rbp) movq %rdi, -64(%rbp) movabsq $jl_apply_generic, %r15 movl $3, %edx movq %r14, %rcx callq *%r15 movq %rax, %rbx movq %rbx, -88(%rbp) movabsq $586874896, %r12 # imm = 0x22FB0010 movq (%r12), %rax testq %rax, %rax jne L198 leaq 98096(%rdi), %rcx movabsq $jl_get_binding_or_error, %rax movl $122868360, %edx # imm = 0x752D288 callq *%rax movq %rax, (%r12) L198: movq 8(%rax), %rax testq %rax, %rax je L263 movq %rax, -80(%rbp) addq $5498232, %rdi # imm = 0x53E578 movq %rdi, -72(%rbp) movq %rbx, -64(%rbp) movq %rax, -56(%rbp) movl $3, %edx movq %r14, %rcx callq *%r15 movq -96(%rbp), %rcx movq %rcx, (%rsi) addq $96, %rsp popq %rbx popq %rdi popq %rsi popq %r12 popq %r14 popq %r15 popq %rbp retq L263: movabsq $jl_undefined_var_error, %rax movl $122868360, %ecx # imm = 0x752D288 callq *%rax ud2 nopw (%rax,%rax)
Para idiomas dinâmicos sem especialização de tipo, esse código inchado com todas as instruções extras é o melhor possível, então Julia diminui a velocidade. Para entender por que isso é tão importante, observe que cada código que você escreve em Julia é compilado. Digamos que você escreva um loop em seu script:
a = 1 for i = 1:100 a += a + f(a) end
O compilador precisará compilar esse loop, mas, como não pode garantir que os tipos não sejam alterados, envolve um calçado em todos os tipos, o que leva a uma execução lenta.
Como evitar um problema
Existem várias maneiras de evitar esse problema. A maneira mais fácil é sempre envolver seus scripts em funções. Por exemplo, o código anterior assumirá o formato:
function geta(a) # can also just define a=1 here for i = 1:100 a += a + f(a) end return a end a = geta(1)
Isso fornecerá o mesmo resultado, mas como o compilador pode se especializar no tipo a , ele fornecerá o código compilado que você deseja. Outra coisa que você pode fazer é definir suas variáveis como constantes.
const b = 5
Ao fazer isso, você informa ao compilador que a variável não será alterada e, portanto, poderá especializar todo o código que a usa no tipo que está atualmente. Há uma pequena peculiaridade de que Julia realmente permite que você altere o valor de uma constante, mas não de um tipo. Assim, você pode usar const para informar ao compilador que você não alterará o tipo. No entanto, observe que existem algumas pequenas peculiaridades:
const a = 5 f() = a println(f()) # Prints 5 a = 6 println(f()) # Prints 5 # WARNING: redefining constant a
isso não funciona como esperado, porque o compilador, percebendo que ele sabe a resposta para f () = a (já que a é uma constante), simplesmente substituiu a chamada de função pela resposta, dando um comportamento diferente do que se a não a constante.
Moral: não escreva seus scripts diretamente no REPL, envolva-os sempre em uma função.
Nezhdanchik dois: instabilidade de tipo
Então, acabei de expressar uma opinião sobre a importância da especialização de código para os tipos de dados. Deixe-me fazer uma pergunta, o que acontece quando seus tipos podem mudar? Se você adivinhou: “Bem, neste caso, você não pode especializar o código compilado”, então você está certo. Esse problema é conhecido como instabilidade de tipo. Eles podem aparecer de maneira diferente, mas um exemplo comum é que você inicializa o valor com o simples, mas não necessariamente o tipo que deve ser. Por exemplo, vejamos:
function g() x=1 for i = 1:10 x = x/2 end return x end
Observe que 1/2 é um número de ponto flutuante em Julia. Portanto, se começamos com x = 1 , o número inteiro mudará para um número de ponto flutuante e, portanto, a função deve compilar o loop interno, como se pudesse ser de qualquer tipo. Se tivéssemos:
function h() x=1.0 for i = 1:10 x = x/2 end return x end
então toda a função poderá compilar de maneira ideal, sabendo que x permanecerá um número de ponto flutuante (essa capacidade do compilador de determinar tipos é chamada de inferência de tipo). Podemos verificar o código compilado para ver a diferença:
Calçado nativo pushq %rbp movq %rsp, %rbp pushq %r15 pushq %r14 pushq %r13 pushq %r12 pushq %rsi pushq %rdi pushq %rbx subq $136, %rsp movl $2147565728, %ebx # imm = 0x800140A0 movabsq $jl_get_ptls_states, %rax callq *%rax movq %rax, -152(%rbp) vxorps %xmm0, %xmm0, %xmm0 vmovups %xmm0, -80(%rbp) movq $0, -64(%rbp) vxorps %ymm0, %ymm0, %ymm0 vmovups %ymm0, -128(%rbp) movq $0, -96(%rbp) movq $18, -144(%rbp) movq (%rax), %rcx movq %rcx, -136(%rbp) leaq -144(%rbp), %rcx movq %rcx, (%rax) movq $0, -88(%rbp) Source line: 4 movq %rbx, -104(%rbp) movl $10, %edi leaq 477872(%rbx), %r13 leaq 10039728(%rbx), %r15 leaq 8958904(%rbx), %r14 leaq 64(%rbx), %r12 leaq 10126032(%rbx), %rax movq %rax, -160(%rbp) nopw (%rax,%rax) L176: movq %rbx, -128(%rbp) movq -8(%rbx), %rax andq $-16, %rax movq %r15, %rcx cmpq %r13, %rax je L272 movq %rbx, -96(%rbp) movq -160(%rbp), %rcx cmpq $2147419568, %rax # imm = 0x7FFF05B0 je L272 movq %rbx, -72(%rbp) movq %r14, -80(%rbp) movq %r12, -64(%rbp) movl $3, %edx leaq -80(%rbp), %rcx movabsq $jl_apply_generic, %rax vzeroupper callq *%rax movq %rax, -88(%rbp) jmp L317 nopw %cs:(%rax,%rax) L272: movq %rcx, -120(%rbp) movq %rbx, -72(%rbp) movq %r14, -80(%rbp) movq %r12, -64(%rbp) movl $3, %r8d leaq -80(%rbp), %rdx movabsq $jl_invoke, %rax vzeroupper callq *%rax movq %rax, -112(%rbp) L317: movq (%rax), %rsi movl $1488, %edx # imm = 0x5D0 movl $16, %r8d movq -152(%rbp), %rcx movabsq $jl_gc_pool_alloc, %rax callq *%rax movq %rax, %rbx movq %r13, -8(%rbx) movq %rsi, (%rbx) movq %rbx, -104(%rbp) Source line: 3 addq $-1, %rdi jne L176 Source line: 6 movq -136(%rbp), %rax movq -152(%rbp), %rcx movq %rax, (%rcx) movq %rbx, %rax addq $136, %rsp popq %rbx popq %rdi popq %rsi popq %r12 popq %r13 popq %r14 popq %r15 popq %rbp retq nop
contra
Feitiço de montador puro pushq %rbp movq %rsp, %rbp movabsq $567811336, %rax # imm = 0x21D81D08 Source line: 6 vmovsd (%rax), %xmm0 # xmm0 = mem[0],zero popq %rbp retq nopw %cs:(%rax,%rax)
Essa diferença no número de cálculos para obter o mesmo valor!
Como encontrar e lidar com a instabilidade de tipo

Nesse ponto, você pode perguntar: "Bem, por que não usar C para não precisar dessas instabilidades?" A resposta é:
- Fácil de encontrar
- Eles podem ser úteis.
Você pode lidar com a instabilidade com barreiras funcionais
Julia fornece a macro code_warntype para mostrar onde estão as instabilidades de tipo. Por exemplo, se usarmos isso na função g que criamos:
@code_warntype g()
obtenha a análise Variables: #self#::#g x::ANY #temp#@_3::Int64 i::Int64 #temp#@_5::Core.MethodInstance #temp#@_6::Float64 Body: begin x::ANY = 1 # line 3: SSAValue(2) = (Base.select_value)((Base.sle_int)(1,10)::Bool,10,(Base.box)(Int64,(Base.sub_int)(1,1)))::Int64 #temp#@_3::Int64 = 1 5: unless (Base.box)(Base.Bool,(Base.not_int)((#temp#@_3::Int64 === (Base.box)(Int64,(Base.add_int)(SSAValue(2),1)))::Bool)) goto 30 SSAValue(3) = #temp#@_3::Int64 SSAValue(4) = (Base.box)(Int64,(Base.add_int)(#temp#@_3::Int64,1)) i::Int64 = SSAValue(3) #temp#@_3::Int64 = SSAValue(4) # line 4: unless (Core.isa)(x::UNION{FLOAT64,INT64},Float64)::ANY goto 15 #temp#@_5::Core.MethodInstance = MethodInstance for /(::Float64, ::Int64) goto 24 15: unless (Core.isa)(x::UNION{FLOAT64,INT64},Int64)::ANY goto 19 #temp#@_5::Core.MethodInstance = MethodInstance for /(::Int64, ::Int64) goto 24 19: goto 21 21: #temp#@_6::Float64 = (x::UNION{FLOAT64,INT64} / 2)::Float64 goto 26 24: #temp#@_6::Float64 = $(Expr(:invoke, :(#temp#@_5), :(Main./), :(x::Union{Float64,Int64}), 2)) 26: x::ANY = #temp#@_6::Float64 28: goto 5 30: # line 6: return x::UNION{FLOAT64,INT64} end::UNION{FLOAT64,INT64}
Observe que no começo dizemos que o tipo x é Any . Ele usará qualquer tipo que não seja designado como strict type , ou seja, é um tipo abstrato que precisa ser encaixotado / verificado em cada etapa. Vemos que, no final, retornamos x como UNION {FLOAT64, INT64} , que é outro tipo não estrito. Isso nos diz que o tipo code_warntype para h , obteremos todos os tipos estritos:
@code_warntype h() Variables: #self#::#h x::Float64 #temp#::Int64 i::Int64 Body: begin x::Float64 = 1.0 # line 3: SSAValue(2) = (Base.select_value)((Base.sle_int)(1,10)::Bool,10,(Base.box)(Int64,(Base.sub_int)(1,1)))::Int64 #temp#::Int64 = 1 5: unless (Base.box)(Base.Bool,(Base.not_int)((#temp#::Int64 === (Base.box)(Int64,(Base.add_int)(SSAValue(2),1)))::Bool)) goto 15 SSAValue(3) = #temp#::Int64 SSAValue(4) = (Base.box)(Int64,(Base.add_int)(#temp#::Int64,1)) i::Int64 = SSAValue(3) #temp#::Int64 = SSAValue(4) # line 4: x::Float64 = (Base.box)(Base.Float64,(Base.div_float)(x::Float64,(Base.box)(Float64,(Base.sitofp)(Float64,2)))) 13: goto 5 15: # line 6: return x::Float64 end::Float64
Isso indica que a função é do tipo estável e será compilada essencialmente em um código C ideal. Portanto, não é difícil encontrar instabilidade de tipo. O mais difícil é encontrar o design certo. Por que resolver instabilidade de tipo? Esse é um problema de longa data que levou ao fato de que as linguagens dinamicamente digitadas dominam o campo de jogo dos scripts. A ideia é que, em muitos casos, você queira encontrar um compromisso entre desempenho e confiabilidade.
Por exemplo, você pode ler uma tabela de uma página da Web na qual números inteiros são misturados com números de ponto flutuante. Em Julia, você pode escrever sua função para que, se todos fossem números inteiros, ele compila bem e, se todos forem números de ponto flutuante, também compile bem. E se eles são misturados? Isso ainda vai funcionar. Essa é a flexibilidade / conveniência que conhecemos e amamos em uma linguagem como Python / R. Mas Julia dirá diretamente ( via code_warntype ) quando você sacrifica o desempenho.
Como lidar com instabilidades de tipo
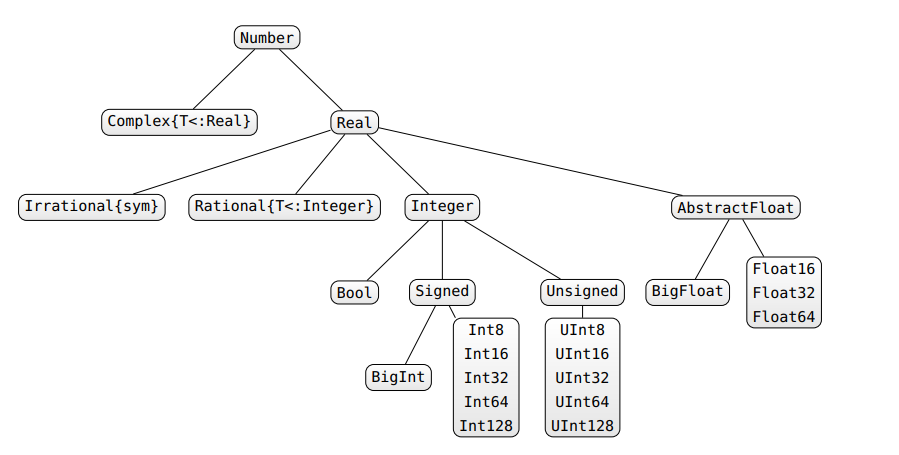
Existem várias maneiras de lidar com instabilidades de tipo. Primeiro de tudo, se você gosta de algo como C / Fortran, onde seus tipos são declarados e não podem mudar (o que garante a estabilidade do tipo), você pode fazer isso em Julia:
local a::Int64 = 5
Isso cria a número inteiro de 64 bits e, se o código futuro tentar alterá-lo, será gerada uma mensagem de erro (ou a conversão correta será executada. Mas, como a conversão não será arredondada automaticamente, provavelmente ocorrerá erros). Polvilhe-os em torno de seu código e você obterá estabilidade de tipo, ala, C / Fortran . Uma maneira menos complicada de lidar com isso é com as instruções de tipo. Aqui você coloca a mesma sintaxe do outro lado do sinal de igual. Por exemplo:
a = (b/c)::Float64
Parece dizer: "calcule b / c e certifique-se de que a saída seja Float64. Caso contrário, tente executar uma conversão automática. Se a conversão não puder ser realizada facilmente, produza um erro". A colocação de tais projetos ajudará você a saber quais tipos estão envolvidos. No entanto, em alguns casos, a instabilidade do tipo é necessária. Por exemplo, digamos que você queira ter um código confiável, mas o usuário fornece algo louco, como:
arr = Vector{Union{Int64,Float64}}(undef, 4) arr[1]=4 arr[2]=2.0 arr[3]=3.2 arr[4]=1
que é uma matriz de números inteiros 4x1 e números de ponto flutuante. O tipo de elemento real para a matriz é Union {Int64, Float64} , que, como vimos anteriormente, não era rigoroso, o que poderia levar a problemas. O compilador sabe apenas que cada valor pode ser um número inteiro ou um número de ponto flutuante, mas não qual elemento de qual tipo. Isso significa que é ingênuo fazer aritmética com essa matriz, por exemplo:
function foo{T,N}(array::Array{T,N}) for i in eachindex(array) val = array[i] # do algorithm X on val end end
será lento, pois as operações serão encaixotadas. No entanto, podemos usar vários despachos para executar códigos de maneira especializada. Isso é conhecido como usar barreiras funcionais. Por exemplo:
function inner_foo{T<:Number}(val::T) # Do algorithm X on val end function foo2{T,N}(array::Array{T,N}) for i in eachindex(array) inner_foo(array[i]) end end
Observe que, devido ao envio múltiplo, chamar inner_foo chama um método especialmente compilado para números de ponto flutuante ou um método especialmente compilado para números inteiros. Assim, você pode colocar um cálculo longo em inner_foo e ainda fazê-lo funcionar bem, não inferior à digitação estrita que a barreira funcional fornece.
Portanto, espero que você veja que Julia ofereça uma boa combinação de forte desempenho de digitação e a conveniência da digitação dinâmica. Uma boa programadora, Julia, tem as duas opções para maximizar a produtividade e / ou a produtividade, se necessário.
Surpresa 3: Eval trabalha globalmente

Um dos maiores pontos fortes de Julia é sua capacidade de metaprogramação. Isso permite que você escreva facilmente programas geradores de código, reduzindo efetivamente a quantidade de código necessária para gravar e manter. Uma macro é uma função que é executada em tempo de compilação e (geralmente) cospe código. Por exemplo:
macro defa() :(a=5) end
substituirá qualquer instância defa pelo código a = 5 ( :(a = 5) é uma expressão citada . O código de Julia é expressões e, portanto, metaprogramação é uma coleção de expressões).
Você pode usar isso para criar qualquer programa Julia complexo que desejar e colocá-lo em uma função como um tipo de atalho realmente inteligente. No entanto, às vezes você pode precisar avaliar diretamente o código gerado. Julia fornece uma função eval ou macro @eval para fazer isso. Em geral, você deve tentar evitar a avaliação, mas existem alguns códigos nos quais é necessário, por exemplo, minha nova biblioteca para transferir dados entre diferentes processos para a programação paralela . , , :
@eval :(a=5)
(REPL). , / . Por exemplo:
function testeval() @eval :(a=5) return 2a+5 end
, a REPL. , , :
function testeval() @eval :(a=5) b = a::Int64 return 2b+5 end
b — , , , , , . eval , , REPL .
4:
Julia , . : , .
, ? , , . Por exemplo:
a = 2 + 3 + 4 + 5 + 6 + 7 +8 + 9 + 10+ 11+ 12+ 13 a
, 90, 27. ? a = 2 + 3 + 4 + 5 + 6 + 7 , a = 27 , +8 + 9 + 10+ 11+ 12+ 13 , , , :
a = 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10+ 11+ 12+ 13
90, . , .
. — , . rssdev10
. Por exemplo:
x = rand(2,2) a = [cos(2*pi.*x[:,1]).*cos(2*pi.*x[:,2])./(4*pi) -sin(2.*x[:,1]).*sin(2.*x[:,2])./(4)] b = [cos(2*pi.*x[:,1]).*cos(2*pi.*x[:,2])./(4*pi) - sin(2.*x[:,1]).*sin(2.*x[:,2])./(4)]
, a b — , ! (2,2) , — (1-) 2. , , :
a = [1 -2] b = [1 - 2]
: 1 -2 . : 1-2 . - . :
a = [1 2 3 -4 2 -3 1 4]
2x4. , . : hcat :
a = hcat(cos(2*pi.*x[:,1]).*cos(2*pi.*x[:,2])./(4*pi),-sin(2.*x[:,1]).*sin(2.*x[:,2])./(4))
!
№5: ,

(View) — () , ( ), .
, , . , . , .
— "". ""
a = [3;4;5] b = a b[1] = 1
, a — [1; 4; 5] , . . b a . , b = a b a . , , b , , ( b a ). , . , , :
a = rand(2,2) # Makes a random 2x2 matrix b = vec(a) # Makes a view to the 2x2 matrix which is a 1-dimensional array
b , b a , b . , , ( , ). . , . Por exemplo:
c = a[1:2,1]
c a ). , , , , . , , :
d = @view a[1:2,1] e = view(a,1:2,1)
d , e — , d e a , , , reshape , .) , . Por exemplo:
a[1:2,1] = [1;2]
a , a[1:2,1] view (a, 1:2,1) , , a . -? , :
b = copy(a)
, b a , , b a . a , copy! (B, a) , a a ( , b ). . , Vector {Vector} :
a = [ [1, 2, 3], [4, 5], [6, 7, 8, 9] ]
b = copy(a) b[1][1] = 10 a
3-element Array{Array{Int64,1},1}: [10, 2, 3] [4, 5] [6, 7, 8, 9]
, a[1][1] 10! ? copy a . a , b , b . , deepcopy :
b = deepcopy(a)
, . , , .
№6: , In-Place
MATLAB / Python / R . Julia , , , " ".
function f() x = [1;5;6] for i = 1:10 x = x + inner(x) end return x end function inner(x) return 2x end
, inner , , 2x . , . , - y , :
function f() x = [1;5;6] y = Vector{Int64}(3) for i = 1:10 inner(y,x) for i in 1:3 x[i] = x[i] + y[i] end copy!(y,x) end return x end function inner!(y,x) for i=1:3 y[i] = 2*x[i] end nothing end
. inner!(y, x) , y . y , y , , , inner! (y, x) ! ( ).
, inner!(y, x) . copy!(y, x) — , x y , . , , . : x y . , x + inner(x) , , , 11 . , .
, , , . - ( loop-fusion ). Julia v0.5 . ( ( broadcast ), f.(x) — , f x , , . f x , x = x + f. (x) . :
x .= x .+ f.(x)
.= , , ,
for i = 1:length(x) x[i] = x[i] + f(x[i]) end
, :
function f() x = [1;5;6] for i = 1:10 x .= x .+ inner.(x) end return x end function inner(x) return 2x end
MATLAB / R / Python , , , .
: ,
: , . , . , . , , . , .
- , C / Fortran , . - , , !
: ? , . , , ? [ , Javascript var x = 3 x , x = 3 x . ? , - Javascript!]