Algoritmos para recomendações, previsões de eventos ou avaliações de risco são uma decisão de tendência em bancos, companhias de seguros e muitos outros setores de negócios. Por exemplo, esses programas ajudam, com base na análise de dados, a sugerir quando um cliente devolverá um empréstimo bancário, qual será a demanda no varejo, qual a probabilidade de um evento segurado ou uma saída de clientes em telecomunicações, etc. Para uma empresa, essa é uma oportunidade valiosa para otimizar suas despesas, aumentar a velocidade do trabalho e, geralmente, melhorar o serviço.
No entanto, abordagens tradicionais, como classificação e regressão, não são adequadas para a construção de tais programas. Considere esse problema como um exemplo de caso que prevê episódios médicos: analisamos as nuances da natureza dos dados e as possíveis abordagens para modelagem, construímos um modelo e analisamos sua qualidade.
O desafio de prever episódios médicos
A previsão de episódios é baseada em uma análise de dados históricos. O conjunto de dados neste caso consiste em duas partes. O primeiro são os dados sobre serviços prestados anteriormente ao paciente. Esta parte do conjunto de dados inclui dados sociodemográficos sobre o paciente, como idade e sexo, além de diagnósticos feitos a ele em diferentes momentos nos procedimentos de codificação ICD10-CM [1] e HCPCS realizados [2]. Esses dados formam sequências no tempo que permitem que você tenha uma idéia da condição do paciente no momento de seu interesse. Para modelos de treinamento e para trabalhar na produção, dados personalizados são suficientes.
A segunda parte do conjunto de dados é uma lista de episódios que ocorrem para o paciente. Para cada episódio, indicamos seu tipo e data de ocorrência, bem como o período de tempo, serviços incluídos e outras informações. A partir desses dados, variáveis de destino para previsão são geradas.
O aspecto do tempo é importante no problema que está sendo resolvido: estamos interessados apenas em episódios que possam surgir em um futuro próximo. Por outro lado, o conjunto de dados à nossa disposição foi coletado por um período limitado de tempo, além do qual não há dados. Assim, não podemos dizer se os episódios ocorrem fora do período de observação, quais são eles, em que momento exato eles surgem. Essa situação é chamada de censura correta.
Da mesma forma, a censura à esquerda ocorre: para alguns pacientes, um episódio pode começar a se desenvolver antes do que está disponível para nossa observação. Para nós, parecerá um episódio que surgiu sem qualquer pano de fundo.
Existe outro tipo de censura dos dados - interrupção da observação (se o período de observação não for concluído e o evento não tiver ocorrido). Por exemplo, devido à movimentação de um paciente, uma falha no sistema de coleta de dados e assim por diante.
Na fig. 1 mostra esquematicamente diferentes tipos de censura de dados. Todos eles distorcem as estatísticas e dificultam a construção de um modelo.
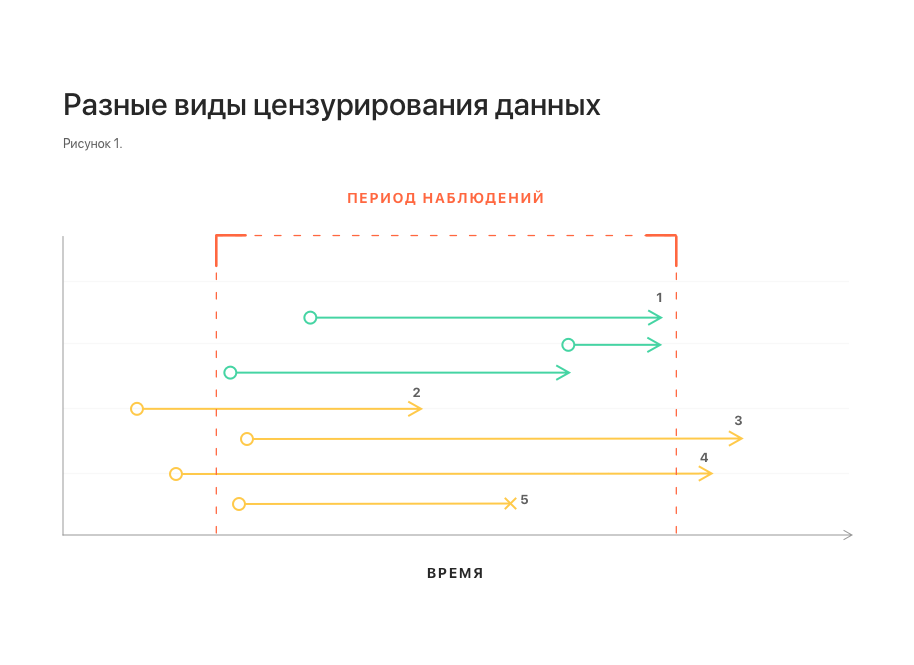Notas: 1 - observações sem censura; 2, 3 - censura esquerda e direita, respectivamente; 4 - censura esquerda e direita ao mesmo tempo;
5 - interrupção da observação.Outro recurso importante do conjunto de dados está relacionado à natureza do fluxo de dados na vida real. Alguns dados podem chegar atrasados, caso em que não estão disponíveis no momento da previsão. Para levar esse recurso em consideração, é necessário complementar o conjunto de dados jogando vários elementos da cauda de cada sequência.
Classificação e Regressão
Naturalmente, o primeiro pensamento será reduzir o problema à bem conhecida classificação e regressão. No entanto, essas abordagens encontram sérias dificuldades.
Por que a regressão não nos convém, fica claro a partir dos fenômenos considerados de censura à direita e à esquerda: a distribuição do tempo de ocorrência de um episódio no conjunto de dados pode ser alterada. Além disso, a magnitude e o fato da presença desse viés não podem ser determinados usando o próprio conjunto de dados. O modelo construído pode mostrar resultados arbitrariamente bons com qualquer abordagem de validação, mas isso, muito provavelmente, não terá nada a ver com sua adequação à previsão de dados de produção.
Mais promissor, à primeira vista, é uma tentativa de reduzir o problema à classificação: definir um determinado período de tempo e determinar o episódio que surgirá nesse período. A principal dificuldade aqui é a ligação do intervalo de tempo de interesse para nós. Ele pode ser vinculado de maneira confiável apenas ao momento da última atualização do histórico do paciente. Ao mesmo tempo, a solicitação para a previsão do episódio não está vinculada ao tempo e pode ocorrer a qualquer momento, tanto dentro desse período (e, em seguida, o período de interesse efetivo é encurtado) quanto completamente fora dele - e então a previsão geralmente perde seu significado (ver Fig. 2) Isso naturalmente induz um aumento no período de interesse, o que acaba reduzindo o valor da previsão de qualquer maneira.
Notas: 1 - atualiza a história do paciente; 2 - a atualização mais recente e o período de tempo associado a ela; 3, 4 - solicitações de previsão de episódios recebidas durante esse período. É visto que o intervalo de previsão efetivo para eles é menor; 5 - solicitação recebida fora do intervalo. Para ele, a previsão é impossível.Análise de sobrevivência
Como alternativa, podemos considerar a abordagem, na literatura russa chamada análise de sobrevivência (análise de sobrevivência ou análise de tempo até o evento) [3]. Esta é uma família de modelos projetados especificamente para trabalhar com dados censurados. Baseia-se na aproximação da função de risco (função de risco, intensidade de ocorrência de eventos), que estima a distribuição de probabilidade da ocorrência de um evento ao longo do tempo. Essa abordagem permite considerar corretamente a presença de diferentes tipos de censura.
Para o problema que está sendo resolvido, essa abordagem também permite combinar os dois aspectos do problema em um modelo: determinar o tipo de episódio e prever o tempo de sua ocorrência. Para fazer isso, basta criar um modelo separado para cada tipo de episódio, semelhante à abordagem one-vs-all na classificação. Em seguida, a ocorrência de um episódio não alvo pode ser interpretada como a exclusão de um objeto da amostra observada sem a ocorrência de um evento, que é outro tipo de censura aos dados e também é corretamente levado em consideração pelo modelo. Essa interpretação está correta do ponto de vista da lógica comercial: se um paciente é submetido a uma cirurgia de catarata, isso não exclui a ocorrência de outros episódios para ele no futuro.
Entre a família de modelos para análise de sobrevivência, duas variedades podem ser distinguidas: analítica e regressão. Os modelos analíticos são puramente descritivos, são construídos para toda a população, não levam em consideração as características de seus membros individuais e, portanto, só podem prever a ocorrência de um evento para algum membro típico da população. Diferentemente da analítica, os modelos de regressão são construídos levando em consideração as características de membros individuais da população e permitem que sejam feitas previsões também para membros individuais levando em consideração suas características. nesse problema, foi essa variação que foi usada, ou melhor, o modelo de Risco Proporcional de Cox (doravante - CoxPH).
Regressão de sobrevivência e cirurgia de catarata
A abordagem mais simples será semelhante à regressão convencional: considere a expectativa matemática do tempo do início do evento como a saída. Como o CoxPH recebe dados como um vetor numérico na entrada e nosso conjunto de dados é, de fato, uma sequência de códigos e procedimentos de diagnóstico (dados categóricos), é necessária uma transformação preliminar dos dados:
- Tradução de códigos em uma representação incorporada usando o modelo GloVe previamente treinado [4];
- Agregação de todos os códigos disponíveis no último período da história do paciente em um único vetor;
- Codificação one-hot do sexo do paciente e escala da idade.
Utilizamos os vetores de recursos obtidos para o treinamento do modelo e sua validação. O modelo resultante demonstra os seguintes valores do índice de concordância (índice c ou estatística c) [5]:
- 0,71 para validação 5 vezes;
- 0,69 na amostra pendente.
Isso é comparável ao nível de 0,6-0,7 habitual para esses modelos [6].
No entanto, se você observar o erro absoluto médio entre o tempo previsto previsto de ocorrência do episódio e o real, o erro é de 5 dias. A razão para um erro tão grande é que a otimização para o índice c garante apenas a ordem correta dos valores: se um evento ocorrer antes do outro, os valores previstos do tempo esperado para os eventos serão um menor que o outro, respectivamente. Além disso, nenhuma declaração é feita com relação aos valores previstos.
Outra variante possível do valor de saída do modelo é uma tabela de valores da função de risco em momentos diferentes. Essa opção possui uma estrutura mais complexa, é mais difícil de interpretar do que a anterior, mas ao mesmo tempo fornece mais informações.
Alterar o formato de saída requer uma maneira diferente de avaliar a qualidade do modelo: precisamos garantir que, para exemplos positivos (quando um episódio ocorra), o nível de risco seja mais alto do que para exemplos negativos (quando um episódio não ocorrer). Para fazer isso, para cada distribuição prevista da função de risco na amostra atrasada, passaremos da tabela de valores para um valor - o máximo. Tendo contado os valores medianos para exemplos positivos e negativos, veremos que eles diferem de maneira confiável: 0,13 versus 0,04, respectivamente.
Em seguida, usamos esses valores para construir a curva ROC e calcular a área abaixo dela - ROC AUC, que é 0,92, o que é aceitável para o problema que está sendo resolvido.
Conclusão
Assim, vimos que a análise de sobrevivência é a melhor abordagem para solucionar o problema de previsão de episódios médicos, levando em consideração todas as nuances do problema e os dados disponíveis. No entanto, sua aplicação implica um formato diferente da saída do modelo e uma abordagem diferente para avaliar sua qualidade.
A aplicação do modelo CoxPH na previsão de episódios de cirurgia de catarata nos permitiu alcançar indicadores aceitáveis de qualidade do modelo. Uma abordagem semelhante pode ser aplicada a outros tipos de episódios, mas os indicadores específicos de qualidade dos modelos só podem ser avaliados diretamente no processo de modelagem.
Literatura
[1] Modificação clínica da CID-10
en.wikipedia.org/wiki/ICD-10_Clinical_Modification[2] Sistema de codificação de procedimentos comuns de assistência
médica en.wikipedia.org/wiki/Healthcare_Common_Procedure_Coding_System[3] Análise de sobrevivência
en.wikipedia.org/wiki/Survival_analysis[4] GloVe: vetores globais para representação de palavras
nlp.stanford.edu/projects/glove[5] Estatística C: definição, exemplos, ponderação e importância
www.statisticshowto.datasciencecentral.com/c-statistic[6] VC Raykar et al. Sobre a classificação na análise de sobrevivência: limites no índice de concordância
papers.nips.cc/paper/3375-on-ranking-in-survival-analysis-bounds-on-the-concordance-index.pdf