Introdução:Um grande número dos mais diversos problemas relacionados a quase todos os ramos mais importantes da física matemática e projetados para responder a questões técnicas tópicas está associado à aplicação das funções de Bessel.
As funções de Bessel são amplamente utilizadas na resolução de problemas de acústica, radiofísica, hidrodinâmica, problemas de física atômica e nuclear. Numerosas aplicações das funções de Bessel à teoria da condutividade térmica e à teoria da elasticidade (problemas nas vibrações de placas, problemas na teoria da casca, problemas na determinação da concentração de tensão nas trincas).
Essa popularidade das funções de Bessel é explicada pelo fato de que resolver equações da física matemática contendo o operador Laplace em coordenadas cilíndricas pelo método clássico de separação de variáveis leva a uma equação diferencial ordinária, que serve para determinar essas funções [1].
As funções de Bessel são nomeadas em homenagem ao astrônomo alemão Friedrich Bessel, que em 1824, estudando o movimento dos planetas ao redor do sol, derivou relações de recorrência para funções de Bessel
Jv(x) recebido por números inteiros
v representação integral de uma função
Jv(x) , comprovou a existência de inúmeros zeros de função
J0(x) e compilou as primeiras tabelas para funções
J1(x) e
J2(x) .
Contudo, pela primeira vez, uma das funções de Bessel
J0(x) Foi considerado em 1732 por Daniel Bernoulli em um trabalho dedicado à oscilação de cadeias pesadas. D. Bernoulli encontrou uma expressão de função
J0(x) na forma de uma série de potências e notou (sem prova) que a equação
J0(x)=0 tem inúmeras raízes válidas.
O próximo trabalho, no qual as funções de Bessel são encontradas, foi o trabalho de Leonardo Euler em 1738, dedicado ao estudo das vibrações de uma membrana circular. Neste trabalho, L. Euler encontrou para números inteiros
v Expressão da função Bessel
Jv(x) sob a forma de uma série de poderes
x , e em artigos subsequentes estendeu essa expressão ao caso de valores arbitrários de índice
v . Além disso, L. Euler provou que, para
v igual a um inteiro e meio, funções
Jv(x) expresso através de funções elementares.
Ele observou (sem evidência) que, com validade
v as funções
Jv(x) inúmeros zeros reais e deu uma representação integral para
Jv(x) . Alguns pesquisadores acreditam que os principais resultados relacionados às funções de Bessel e suas aplicações na física matemática estão relacionados ao nome de L. Euler.
Estudar a propriedade das funções de Bessel e, ao mesmo tempo, dominar métodos para resolver equações reduzidas a funções de Bessel, permite o programa de matemática simbólica distribuído gratuitamente SymPy - a biblioteca Python.
No programa de matemática simbólica SymPy, gráficos das funções de Bessel do primeiro tipo de ordens inteiras podem ser construídos usando a relação para a soma de uma série:
Jp(x)= sum inftym=0 fracx2m+p(−1)m22m+pm! Gama(p+m+1)
Funções de Bessel do primeiro tipofrom sympy import* from sympy.plotting import plot x,n, p=var('x,n, p') def besselj(p,x): return summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]) st="J_{p}(x)" p1=plot(besselj(0,x),(x,-20,20),line_color='b',title=' $'+st+ '$',show=False) p2=plot(besselj(1,x),(x,-20,20),line_color='g',show=False) p3=plot(besselj(2,x),(x,-20,20),line_color='r',show=False) p4=plot(besselj(3,x),(x,-20,20),line_color='c',show=False) p1.extend(p2) p1.extend(p3) p1.extend(p4) p1.show()
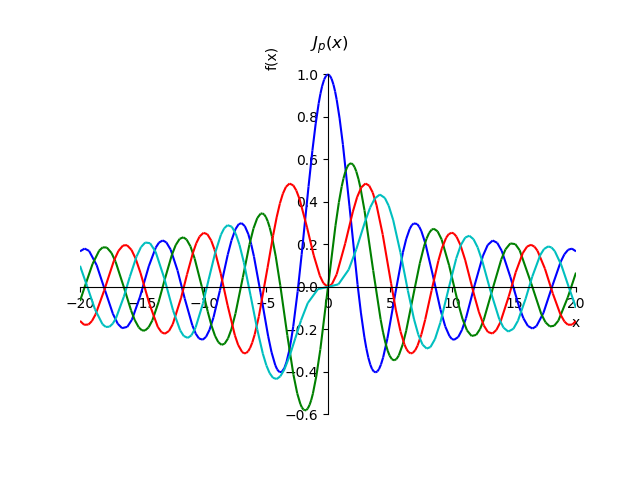
Usando a relação para a soma de uma série, podemos provar a propriedade dessas funções para pedidos inteiros
J1(x)=−J−1(x):
Propriedade da função de Bessel do primeiro tipo from sympy import* from sympy.plotting import plot x,n, p=var('x,n, p') def besselj(p,x): return summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]) st="J_{1}(x)=-J_{-1}(x)" p1=plot(besselj(1,x),(x,-10,10),line_color='b',title=' $'+st+ '$',show=False) p2=plot(besselj(-1,x),(x,-10,10),line_color='r',show=False) p1.extend(p2) p1.show()

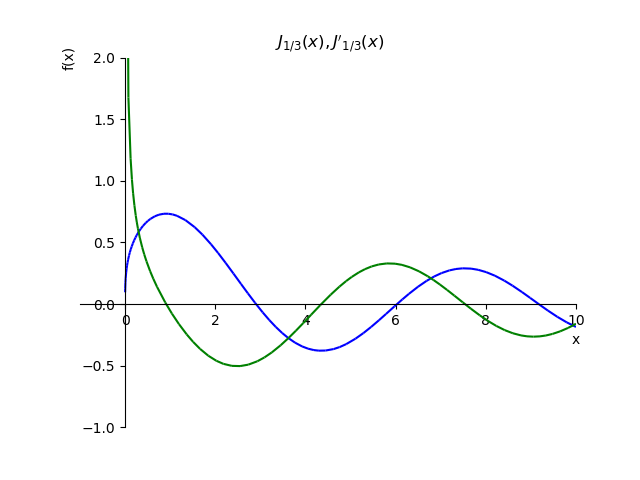
Para demonstrar as condições de Cauchy, construímos uma função
J1/3(x) e seu derivado
fracdJ1/3(x)dx: :
Função de ordem fracionária e sua derivada from sympy import* from sympy.plotting import plot x,n, p=var('x,n, p') def besselj(p,x): return summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]) st="J_{1/3}(x),J{}'_{1/3}(x)" p1=plot(besselj(1/3,x),(x,-1,10),line_color='b',title=' $'+st+ '$',ylim=(-1,2),show=False) def dbesselj(p,x): return diff(summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]),x) p2=plot(dbesselj(1/3,x),(x,-1,10),line_color='g',show=False) p1.extend(p2) p1.show()
No entanto, para cálculos práticos, é usado o maravilhoso módulo mpmath, que permite resolver numericamente não apenas equações com funções de Bessel do primeiro e segundo tipo, incluindo as modificadas de todas as ordens admissíveis, mas também construir gráficos com escala automática.
Além disso, o módulo mpmath não requer ferramentas especiais para compartilhar matemática simbólica e numérica. A história da criação deste módulo e a possibilidade de seu uso para a transformada inversa de Laplace que eu já considerei na publicação [2]. Agora continuamos a discussão sobre mpmath para trabalhar com funções de Bessel [3].
Função de Bessel do primeiro tipo JN(x)mpmath.besselj (n, x, derivativa = 0) - fornece uma função de Bessel do primeiro tipo
Jn(x) . Funções
JN(x) é uma solução para a seguinte equação diferencial:
x2y″+xy′+(x2−n2)y=0
Para todo o positivo
n comporta-se como um seno ou cosseno, multiplicado por um coeficiente que diminui lentamente com
x rightarrow pm inftyFunção de Bessel do primeiro tipo
JN(x) é um caso especial de função hipergeométrica
oF1 :
Jn(x)= fracxn2n Gama(n+1)oF1(n+1, fracx24)
A função Bessel pode ser diferenciada
m vezes, desde que a m-ésima derivada não seja igual a zero:
fracdmdxmJn(x)
Função de Bessel do primeiro tipo
JN(x) para ordens inteiras positivas n = 0,1,2,3 - a solução da equação de Bessel:
from mpmath import* j0 = lambda x: besselj(0,x) j1 = lambda x: besselj(1,x) j2 = lambda x: besselj(2,x) j3 = lambda x: besselj(3,x) plot([j0,j1,j2,j3],[0,14]

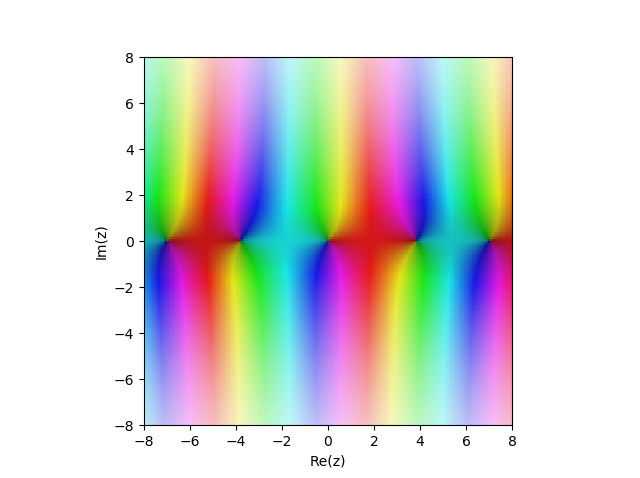
Função de Bessel do primeiro tipo
JN(x) no plano complexo:
from sympy import* from mpmath import* cplot(lambda z: besselj(1,z), [-8,8], [-8,8], points=50000)
Exemplos:
Função
besselj(N,x) fornece um resultado com um determinado número de dígitos
(mp.dps) após vírgula:
from mpmath import* mp.dps = 15; mp.pretty = True print(besselj(2, 1000)) nprint(besselj(4, 0.75)) nprint(besselj(2, 1000j)) mp.dps = 25 nprint( besselj(0.75j, 3+4j)) mp.dps = 50 nprint( besselj(1, pi))
Um argumento de função pode ser um número grande:
from mpmath import* mp.dps = 25 nprint( besselj(0, 10000)) nprint(besselj(0, 10**10)) nprint(besselj(2, 10**100)) nprint( besselj(2, 10**5*j))
As funções de Bessel do primeiro tipo atendem simetrias simples com relação a
x=0 :
from sympy import* from mpmath import* mp.dps = 15 nprint([besselj(n,0) for n in range(5)]) nprint([besselj(n,pi) for n in range(5)]) nprint([besselj(n,-pi) for n in range(5)])
As raízes não são periódicas, mas a distância entre raízes sucessivas se aproxima assintoticamente
2π . As funções de Bessel do primeiro tipo têm o seguinte código:
from mpmath import* print(quadosc(j0, [0, inf], period=2*pi)) print(quadosc(j1, [0, inf], period=2*pi))
Para
n=1/2 ou
n=−1/2 A função de Bessel é reduzida a uma função trigonométrica:
from sympy import* from mpmath import* x = 10 print(besselj(0.5, x)) print(sqrt(2/(pi*x))*sin(x)) print(besselj(-0.5, x)) print(sqrt(2/(pi*x))*cos(x))
É possível calcular derivativos de qualquer ordem,
ordens negativas correspondem à integração :
from mpmath import* mp.dps = 25 print(besselj(0, 7.5, 1)) print(diff(lambda x: besselj(0,x), 7.5)) print(besselj(0, 7.5, 10)) print(diff(lambda x: besselj(0,x), 7.5, 10)) print(besselj(0,7.5,-1) - besselj(0,3.5,-1)) print(quad(j0, [3.5, 7.5]))
A diferenciação com ordem não-número inteiro fornece uma derivada fracionária no sentido da integral diferencial de Riemann-Liouville, calculada usando a função
difint() :
from mpmath import* mp.dps = 15 print(besselj(1, 3.5, 0.75)) print(differint(lambda x: besselj(1, x), 3.5, 0.75))
Outras maneiras de chamar a função Bessel do primeiro tipo de zero e primeiras ordens
mpmath.j0 (x) - Calcula a função Bessel
J0(x) ;
mpmath.j1 (x) - Calcula a função Bessel
J1(x) ;
Funções de Bessel do segundo tipobessely (n, x, derivada = 0) Calcula a função de Bessel de segundo tipo a partir da relação:
Yn(x)= fracJn(x)cos( pi cdotn)−J−n(x)sin( pi cdotn)
Para um número inteiro
n A fórmula a seguir deve ser entendida como o limite. A função Bessel pode ser diferenciada
m vezes desde que a m-ésima derivada não seja igual a zero:
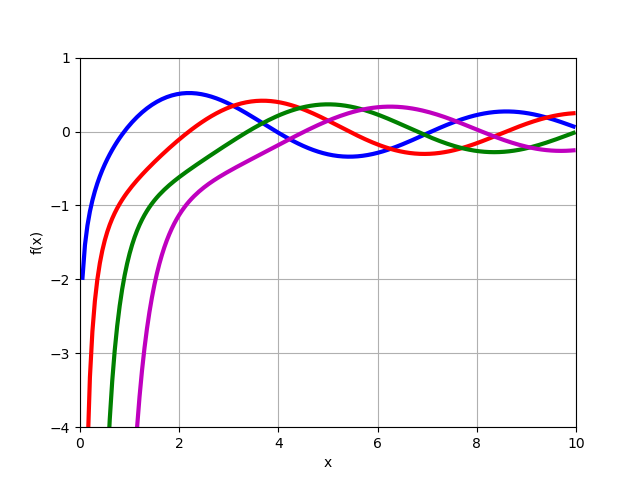
fracdmdxmYn(x)Função de Bessel do segundo tipo
Yn(x) para pedidos positivos inteiros
n=0,1,2,3 .
from sympy import* from mpmath import* y0 = lambda x: bessely(0,x) y1 = lambda x: bessely(1,x) y2 = lambda x: bessely(2,x) y3 = lambda x: bessely(3,x) plot([y0,y1,y2,y3],[0,10],[-4,1])
2ª função tipo Bessel
Yn(x) no plano complexo
from sympy import* from mpmath import* cplot(lambda z: bessely(1,z), [-8,8], [-8,8], points=50000)
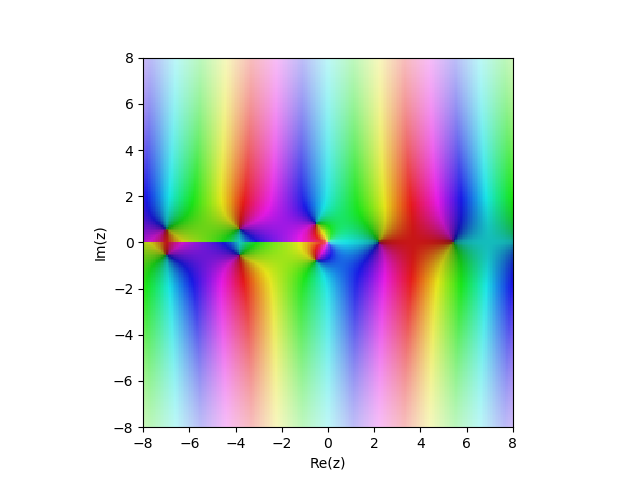
Exemplos:
Alguns valores de função
Yn(x) :
from sympy import* from mpmath import* mp.dps = 25; mp.pretty = True print(bessely(0,0)) print(bessely(1,0)) print(bessely(2,0)) print(bessely(1, pi)) print(bessely(0.5, 3+4j))
Os argumentos podem ser grandes:
from sympy import* from mpmath import* mp.dps = 25; mp.pretty = True print(bessely(0, 10000)) print(bessely(2.5, 10**50)) print(bessely(2.5, -10**50))
Derivados de qualquer ordem, inclusive negativos, podem ser calculados:
from sympy import* from mpmath import* mp.dps = 25; mp.pretty = True print(bessely(2, 3.5, 1)) print(diff(lambda x: bessely(2, x), 3.5)) print(bessely(0.5, 3.5, 1)) print(diff(lambda x: bessely(0.5, x), 3.5)) print(diff(lambda x: bessely(2, x), 0.5, 10)) print(bessely(2, 0.5, 10)) print(bessely(2, 100.5, 100)) print(quad(lambda x: bessely(2,x), [1,3])) print(bessely(2,3,-1) - bessely(2,1,-1))
Função de Bessel modificada do primeiro tipo
mpmath.besseli(n, x, derivative=0)
besseli (n, x, derivada = 0) modificou a função de Bessel do primeiro tipo
In(x)= mathiti−nJn(ix)
fracdmdxmIn(x)
Função de Bessel Modificada
In(x) para pedidos reais
n=0,1,2,3 :
from mpmath import* i0 = lambda x: besseli(0,x) i1 = lambda x: besseli(1,x) i2 = lambda x: besseli(2,x) i3 = lambda x: besseli(3,x) plot([i0,i1,i2,i3],[0,5],[0,5])
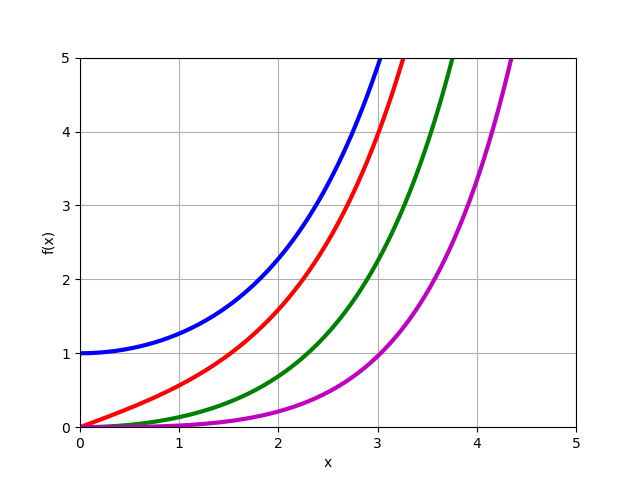
Função de Bessel Modificada
In(x) no plano complexo
from mpmath import* cplot(lambda z: besseli(1,z), [-8,8], [-8,8], points=50000)

Exemplos:
Alguns significados
In(x) from mpmath import* mp.dps = 25; mp.pretty = True print(besseli(0,0)) print(besseli(1,0)) print(besseli(0,1)) print(besseli(3.5, 2+3j))
Os argumentos podem ser grandes:
from mpmath import* mp.dps = 25; mp.pretty = True print(besseli(2, 1000)) print(besseli(2, 10**10)) print(besseli(2, 6000+10000j))
Para números inteiros n, a seguinte representação integral é válida:
from mpmath import* mp.dps = 15; mp.pretty = True n = 3 x = 2.3 print(quad(lambda t: exp(x*cos(t))*cos(n*t), [0,pi])/pi) print(besseli(n,x))
Derivados de qualquer ordem podem ser calculados:
from mpmath import* mp.dps = 25; mp.pretty = True print(besseli(2, 7.5, 1)) print(diff(lambda x: besseli(2,x), 7.5)) print(besseli(2, 7.5, 10)) print(diff(lambda x: besseli(2,x), 7.5, 10)) print(besseli(2,7.5,-1) - besseli(2,3.5,-1)) print(quad(lambda x: besseli(2,x), [3.5, 7.5]))
Funções modificadas de Bessel do segundo tipo,
mpmath.besselk(n, x)
besselk (n, x) funções de Bessel de segundo tipo modificadas
Kn(x)= frac pi4 fracI−n(x)−In(x)sin( pi cdotn)
Para um número inteiro
n essa fórmula deve ser entendida como um limite.
Função de Bessel modificada do 2º tipo
Kn(x) para material
n=0,1,2,3 :
from mpmath import* k0 = lambda x: besselk(0,x) k1 = lambda x: besselk(1,x) k2 = lambda x: besselk(2,x) k3 = lambda x: besselk(3,x) plot([k0,k1,k2,k3],[0,8],[0,5])
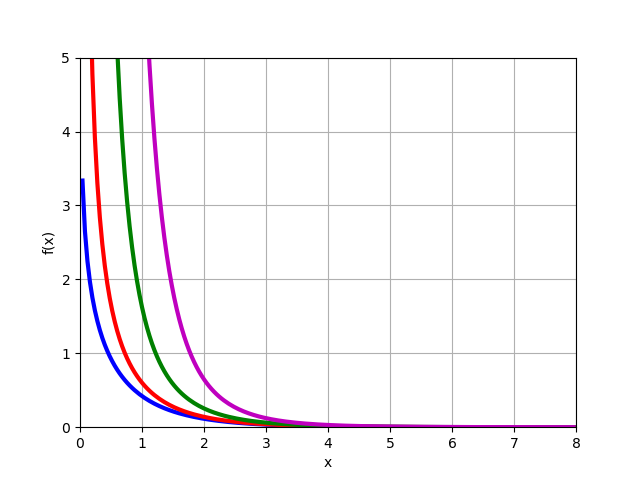
Função de Bessel modificada do 2º tipo
Kn(x)) no plano complexo
from mpmath import* cplot(lambda z: besselk(1,z), [-8,8], [-8,8], points=50000)
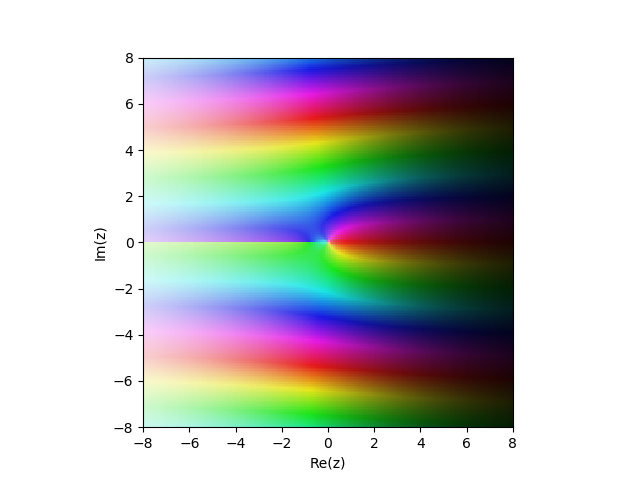
Exemplos:
Argumentos complicados e complexos:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselk(0,1)) print(besselk(0, -1)) print(besselk(3.5, 2+3j)) print(besselk(2+3j, 0.5))
Argumentos são grandes números
from mpmath import * mp.dps = 25; mp.pretty = True print(besselk(0, 100)) print(besselk(1, 10**6)) print(besselk(1, 10**6*j)) print(besselk(4.5, fmul(10**50, j, exact=True)))
Características do comportamento de uma função em um ponto
x=0 :
from mpmath import * print(besselk(0,0)) print(besselk(1,0)) for n in range(-4, 5): print(besselk(n, '1e-1000'))
Zeros da função de Bessel besseljzero() mpmath.besseljzero(v, m, derivative=0)
Por ordem real
mathit nu geq0 e um número inteiro positivo
m retorna
j nu,m , o mésimo zero positivo da função Bessel do primeiro tipo
J nu(z) (veja
besselj () ). Alternativamente, com
derivado=1 dá o primeiro zero primo não negativo
j′ nu,m de
J′ nu(z) . Designações de contratos de indexação usando Abramowitz & Stegun e DLMF. Preste atenção a um caso especial.
j′0,1=0 enquanto todos os outros zeros são positivos.
Na realidade, apenas zeros simples são calculados (todos os zeros das funções de Bessel são simples, exceto quando
z=0 ) e
j nu,m torna-se uma função monotônica de
nu e
m . Os zeros se alternam de acordo com as desigualdades:
j′ nu,k<j nu,k<j′ nu,k+1
j nu,1<j nu+1,2<j nu,2<j nu+1,2<j nu,3 cdots
Exemplos:
Zeros à esquerda das funções de Bessel
J0(z) ,
J1(z) ,
J2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0,1)) print(besseljzero(0,2)) print(besseljzero(0,3)) print(besseljzero(1,1)) print(besseljzero(1,2)) print(besseljzero(1,3)) print(besseljzero(2,1)) print(besseljzero(2,2)) print(besseljzero(2,3))
Zeros à esquerda de derivadas de funções de Bessel
J′0(z) ,
J′1(z) ,
J′2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0,1,1)) print(besseljzero(0,2,1)) print(besseljzero(0,3,1)) print(besseljzero(1,1,1)) print(besseljzero(1,2,1)) print(besseljzero(1,3,1)) print(besseljzero(2,1,1)) print(besseljzero(2,2,1)) print(besseljzero(2,3,1))
Zeros com um índice grande:
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0,100)) print(besseljzero(0,1000)) print(besseljzero(0,10000)) print(besseljzero(5,100)) print(besseljzero(5,1000)) print(besseljzero(5,10000)) print(besseljzero(0,100,1)) print(besseljzero(0,1000,1)) print(besseljzero(0,10000,1))
Zeros de funções com uma ordem grande:
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(50,1)) print(besseljzero(50,2)) print(besseljzero(50,100)) print(besseljzero(50,1,1)) print(besseljzero(50,2,1)) print(besseljzero(50,100,1))
Zeros de funções com ordem fracionária:
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0.5,1)) print(besseljzero(1.5,1)) print(besseljzero(2.25,4))
E
J nu(z) . e
J′ nu(z) pode ser expresso como produtos infinitos em seus zeros:
from mpmath import * mp.dps = 6; mp.pretty = True v,z = 2, mpf(1) nprint((z/2)**v/gamma(v+1) * \ nprod(lambda k: 1-(z/besseljzero(v,k))**2, [1,inf])) print(besselj(v,z)) nprint((z/2)**(v-1)/2/gamma(v) * \ nprod(lambda k: 1-(z/besseljzero(v,k,1))**2, [1,inf])) print(besselj(v,z,1))
besselyzero() mpmath.besselyzero(v, m, derivative=0)
Por ordem real
mathit nu geq0 e um número inteiro positivo
m retorna
y nu,m ,
m , mésimo zero positivo do segundo tipo de função Bessel
Y nu(z) (veja
Bessely () ). Alternativamente, com
derivado=1 dá o primeiro zero positivo
y′ nu,m de
Y′ nu(z) . Os zeros se alternam de acordo com as desigualdades:
y nu,k<y′ nu,k<y nu,k+1
y nu,1<y nu+1,2<y nu,2<y nu+1,2<y nu,3 cdots
Exemplos:
Zeros à esquerda das funções de Bessel
Y0(z) ,
Y1(z) ,
Y2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0,1)) print(besselyzero(0,2)) print(besselyzero(0,3)) print(besselyzero(1,1)) print(besselyzero(1,2)) print(besselyzero(1,3)) print(besselyzero(2,1)) print(besselyzero(2,2)) print(besselyzero(2,3))
Zeros à esquerda de derivadas de funções de Bessel
Y′0(z) ,
Y′1(z) ,
Y′2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0,1,1)) print(besselyzero(0,2,1)) print(besselyzero(0,3,1)) print(besselyzero(1,1,1)) print(besselyzero(1,2,1)) print(besselyzero(1,3,1)) print(besselyzero(2,1,1)) print(besselyzero(2,2,1)) print(besselyzero(2,3,1))
Zeros com um índice grande:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0,100)) print(besselyzero(0,1000)) print(besselyzero(0,10000)) print(besselyzero(5,100)) print(besselyzero(5,1000)) print(besselyzero(5,10000)) print(besselyzero(0,100,1)) print(besselyzero(0,1000,1)) print(besselyzero(0,10000,1))
Zeros de funções com uma ordem grande:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(50,1)) print(besselyzero(50,2)) print(besselyzero(50,100)) print(besselyzero(50,1,1)) print(besselyzero(50,2,1)) print(besselyzero(50,100,1))
Zeros de funções com ordem fracionária:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0.5,1)) print(besselyzero(1.5,1)) print(besselyzero(2.25,4))
Aplicações da Função BesselA importância das funções de Bessel se deve não apenas ao aparecimento frequente da equação de Bessel em aplicações, mas também ao fato de que as soluções de muitas outras equações diferenciais lineares de segunda ordem podem ser expressas em termos de funções de Bessel. Para ver como eles aparecem, começamos com a equação de ordem de Bessel
p sob a forma de:
z2 fracd2wdz2+z fracdwdz+(z2−p2)w=0,(1)
e substitua aqui
w=x− alpha,z=kx beta,(2)
Em seguida, usando (2) e introduzindo as constantes
A,B,C da equação (1), obtemos:
x2y″+Axy′+(B+Cxq)y=0,(3)
A=1−2 alpha,B= alpha2− beta2p2,C= beta2k2,q=2 beta,(4)
Da equação (4) obtemos:
\ left \ {\ begin {matrix} \ alpha = \ frac {1-A} {2}, \\ \ beta = \ frac {q} {2}, \\ k = \ frac {2 \ sqrt {C }} {q} \\ p = \ frac {\ sqrt {(1-A ^ {2} -4B}} {q} \\ \ end {matrix} \ right. (5)
Se
C>0 ,
q neq0 ,
(1−A)2 geqslant4B , a solução geral (para
x>0 ) da equação (3) tem a forma:
y(x)=x alpha left[c1Jp(kx beta)+c2J−p(kx beta) direita](6)
onde:
alpha ,
beta ,
k são determinados a partir do sistema (5). Se
p É um número inteiro então
Jp precisa ser substituído por
Yp .
Flexão longitudinal da coluna verticalVamos agora considerar uma tarefa que é importante para aplicações práticas. Nesta tarefa, é necessário determinar quando uma coluna vertical uniforme é dobrada com seu próprio peso. Nós supomos
x=0 na extremidade superior livre da coluna e
x=L>0 na sua base; assumimos que a base é rigidamente inserida (isto é, fixa imóvel) na base (no solo), possivelmente no concreto.
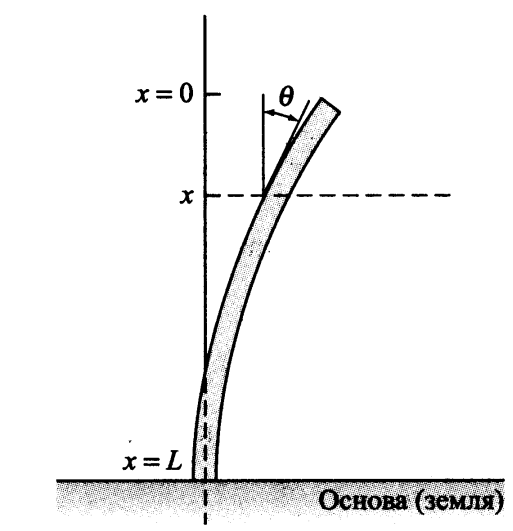
Indique o desvio angular da coluna no ponto
x através de
theta(x) . Da teoria da elasticidade sob essas condições, segue-se que:
EI fracd2 thetadx2+g rhox theta=0,(7)
onde
E - módulo de Young do material da coluna,
I - momento de inércia de sua seção transversal,
rho - densidade linear da coluna e
g - aceleração gravitacional. As condições de contorno são da forma:
theta′(0)=0, theta(L)=0,(8)
Resolveremos o problema usando (7) e (8) com:
lambda= gama2= fracg rhoEI(9)
Reescrevemos (7) levando em conta (9) na condição (8):
fracd2 thetadx2+ gama2x theta=0; fracd thetadx=0, theta(L)=0.(10)
Uma coluna pode ser deformada apenas se houver uma solução não trivial para o problema (10); caso contrário, a coluna permanecerá em uma posição não desviada da vertical (ou seja, fisicamente incapaz de se desviar da vertical).
A equação diferencial (10) é uma equação Airy. A equação (10) tem a forma da equação (3) para
A=B=0 ,
C= gama2 ,
q=3 . Do sistema de equações (5) obtemos
alpha= frac12 ,
beta= frac32 ,
k= frac23 gama ,
p= frac13 .
Portanto, a solução geral tem a forma:
theta(x)=x1/2 left[c1J1/3( frac23 gamax3/2)+c2J−1/3( frac23 gamax3/2) right].(11)
Para aplicar as condições iniciais, substituímos
p= pm frac13 em
Jp= sum inftym=0 frac(−1)mm! Gamma(p+m+1) left( fracx2 direita)2m+p(12)
Após a transformação (12), considerando a solução (11), obtemos:
theta(x)= fracc1 gamma1/331/3 Gamma(4/3) left(x− frac gamma2x412+ frac gama4x7504− cdot cdot cdot right)++ fracc231/3 gamma1/3 Gamma( frac23) left(1− frac gamma2x36+ frac gama4x6180− cdot cdot cdot right).(13)
Fornecido no ponto de partida
theta′(0)=0 nós temos
c1=0 , então (11) assume a forma:
theta(x)=c2x1/2J−1/3( frac23 gamax3/2),(14)
Fornecido no ponto final
theta(L)=0 , de (14), obtemos:
J−1/3( frac23 gamaL3/2)=0(15)
Note-se que as transformações (13), (14) não poderiam ser feitas se os gráficos de funções fossem construídos
J1/3(x),J−1/3(x) usando os recursos considerados do módulo mpmath:
from mpmath import* mp.dps = 6; mp.pretty = True f=lambda x: besselj(-1/3,x) f1=lambda x: besselj(1/3,x) plot([f,f1], [0, 15])
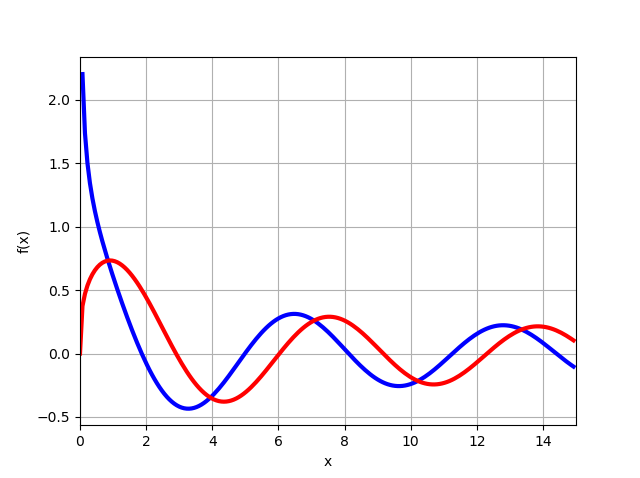
A partir do gráfico, segue-se que para x = 0 a função
J1/3(0)=0 e considerando a solução (11), obtemos imediatamente a equação necessária (15), resta apenas encontrar z, como será mostrado abaixo.
Assim, a coluna é deformada apenas se
z= frac23 gamaL3/2 É a raiz da equação
J−1/3(z)=0 . Construir uma função
J−1/3(z) em um gráfico separado:
from mpmath import* mp.dps = 6; mp.pretty = True f=lambda x: besselj(-1/3,x) plot(f, [0, 15])

O gráfico mostra que a primeira raiz é um pouco menor que 2. Encontre a raiz
z0 da equação
J−1/3(z)=0 Você pode, usando a função
findroot (f, z0) , aceitar, de acordo com o gráfico, o ponto de pesquisa
x0=1 e seis casas decimais
mp.dps = 6 :
from mpmath import* mp.dps = 6; mp.pretty = True f=lambda x: besselj(-1/3,x) print("z0=%s"%findroot(f, 1)
Temos:
z0=1.86635Calculamos o comprimento crítico, por exemplo, um mastro de bandeira, usando a fórmula (15):
Altura do mastro para diferentes parâmetros na seção from numpy import* def LRr(R,r): E=2.9*10**11
Temos:
8.47 m
10,25 m
Um mastro oco pode ser maior que um sólido.
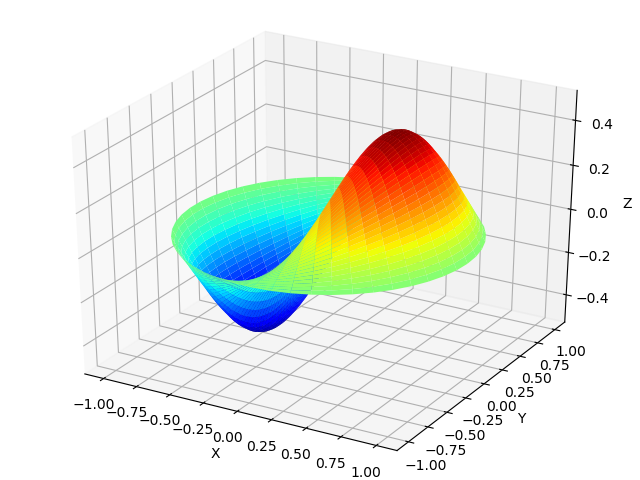
Propagação de ondas em uma membrana fina.
Uma fina membrana quando as ondas sonoras entram, não apenas oscila com a frequência das ondas. A forma de vibrações de membrana pode ser obtida nas funções de Bessel, de acordo com a listagem a seguir, usando as fórmulas
besselj () e
besseljzero () :
Forma de onda da membrana from mpmath import* from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm def Membrana(r): mp.dps=25 return cos(0.5) * cos( theta) *float(besselj(1,r*besseljzero(1,1) ,0)) theta =linspace(0,2*pi,50) radius = linspace(0,1,50) x = array([r * cos(theta) for r in radius]) y = array([r * sin(theta) for r in radius]) z = array([Membrana(r) for r in radius]) fig = plt.figure("") ax = Axes3D(fig) ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel('X') ax.set_ylabel('Y') ax.set_zlabel('Z') plt.show()
Alternativa ao módulo mpmath em funções especiais de Bessel da biblioteca SciPy
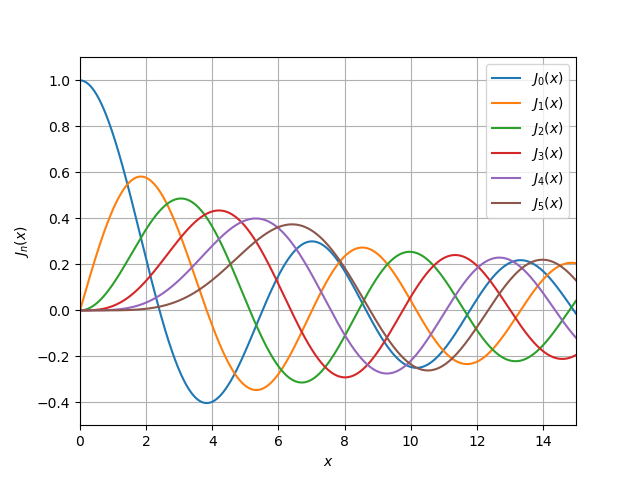
Sem me aprofundar em uma discussão detalhada das funções de Bessel da biblioteca SciPy [4], darei apenas duas listagens para plotar funções do primeiro e do segundo tipo
jv (v, x) ,
yv (v, x) :
jv (v, x) import numpy as np import pylab as py import scipy.special as sp x = np.linspace(0, 15, 500000) for v in range(0, 6): py.plot(x, sp.jv(v, x)) py.xlim((0, 15)) py.ylim((-0.5, 1.1)) py.legend(('$J_{0}(x)$', '$ J_{1}(x)$', '$J_{2}(x)$', '$J_{3}(x)$', '$ J_{4}(x)$','$ J_{5}(x)$'), loc = 0) py.xlabel('$x$') py.ylabel('${J}_n(x)$') py.grid(True) py.show()
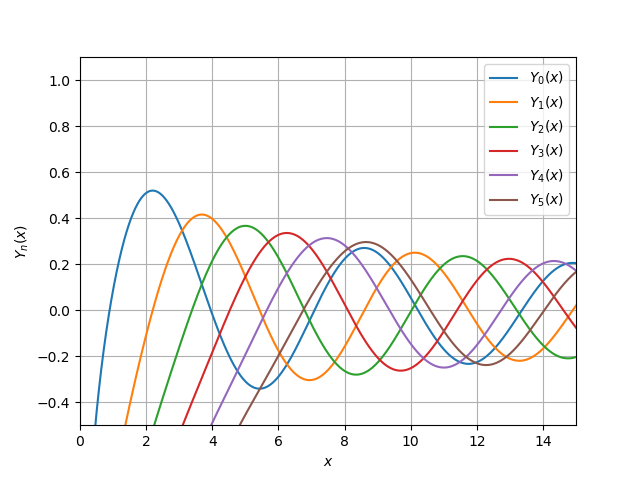
yv (v, x) import numpy as np import pylab as py import scipy.special as sp x = np.linspace(0, 15, 500000) for v in range(0, 6): py.plot(x, sp.yv(v, x)) py.xlim((0, 15)) py.ylim((-0.5, 1.1)) py.legend(('$Y_{0}(x)$', '$ Y_{1}(x)$', '$Y_{2}(x)$', '$Y_{3}(x)$', '$ Y_{4}(x)$','$ Y_{5}(x)$'), loc = 0) py.xlabel('$x$') py.ylabel('$Y_{n}(x)$') py.grid(True) py.show()
Conclusões:
O artigo descreve os conceitos básicos de trabalho com funções de Bessel usando as bibliotecas mpmath, sympy e scipy, fornece exemplos de uso de funções para resolver equações diferenciais. O artigo pode ser útil no estudo das equações da física matemática.
Referências:
1.
Funções de Bessel2.
Usando a conversão inversa de Laplace para analisar os links dinâmicos dos sistemas de controle3.
Funções relacionadas à função de Bessel4.
Funções especiais (scipy.special).