A conversão rápida de modelos é uma prática comum na simulação da física das deformações, bem como em jogos com conteúdo modificado e gerado dinamicamente. Nesses casos, é conveniente aplicar métodos de edição processual e criação de geometria. Estes últimos geralmente permitem salvar bytes estimados ao transmitir dados baixados da rede. Além disso, é divertido!
O artigo visa aumentar as habilidades de processamento processual de malhas no Unity. Falaremos sobre as operações de transformação e geração de partes de uma malha.
Nosso kit para edição de procedimentos de modelos 3D inclui três operações básicas: triangulação, movimento de pontos, extrusão. Falaremos em detalhes sobre os dois últimos. Primeiro, considere as operações de movimento mais simples - vértices em movimento, arestas e triângulos em rotação e escala. Em seguida, trataremos de um dos métodos para gerar nova geometria - a operação de extrusão.
Em uma publicação anterior, descrevemos nossa estrutura para um trabalho conveniente com dados de modelos 3D.Código da estruturapublic static class CustomMeshPool { private static List<CustomMesh> Pool; private static int pointer; public static CustomMesh GetMesh(int id) { return Pool[id]; } public static int Push(CustomMesh customMesh) { if (Pool == null) Pool = new List<CustomMesh>(); pointer = GetAvailableIndex(); if (pointer < Pool.Count) Pool[pointer] = customMesh; else Pool.Add(customMesh); return pointer; } public static bool Remove(int index) { if (Pool == null) return false; var b = Pool[index] == null; Pool[index] = null; return b; } public static int GetAvailableIndex() { if (Pool == null) return 0; var availableIndex = Pool.FindIndex(mesh => mesh == null); return availableIndex != -1 ? availableIndex : Pool.Count; } public static void Flush() { if (Pool != null) Pool.Clear(); } } public class CustomMesh { public int Id; public Triangle[] Triangles; public Vector3[] vertices; public Vector3[] normals; public Vector2[] uv0, uv2; public Color[] colors; public CustomMesh(Vector3[] vertices, int[] triangles, Vector3[] normals, Vector2[] uv0, Vector2[] uv2, Color[] colors) { this.vertices = vertices; this.normals = normals; if (normals != null) for (var i = 0; i < this.normals.Length; i++) { this.normals[i] = this.normals[i].normalized; } this.uv0 = uv0; this.uv2 = uv2; this.colors = colors; var ptr = CustomMeshPool.GetAvailableIndex(); CustomMeshPool.Push(this); Id = ptr; Triangles = new Triangle[triangles.Length / 3]; Triangles = Triangles .AsParallel() .Select((t, i) => new Triangle(ptr, i, triangles[i * 3], triangles[i * 3 + 1], triangles[i * 3 + 2])) .ToArray(); } } public struct Triangle { private int _index; public int Index { get { return _index; } set { _index = value; if (_edges != null) { _edges[0].TriangleIndex = value; _edges[1].TriangleIndex = value; _edges[2].TriangleIndex = value; } } } private int _meshId; public int MeshId { get { return _meshId; } internal set { _meshId = value; } } private Edge[] _edges; public Edge[] Edges { get { return _edges; } set { if (value.Length == 3) { _edges = value; for (var i = 0; i < 3; i++) { _edges[i].TriangleIndex = _index; } } else throw new IndexOutOfRangeException(); } } public Vertex V0 { get { return Edges[0].v0; } set { if (value.MeshId != MeshId) throw new Exception("Not the same mesh"); Edges[0].v0 = value; Edges[2].v1 = value; } } public Vertex V1 { get { return Edges[1].v0; } set { if (value.MeshId != MeshId) throw new Exception("Not the same mesh"); Edges[1].v0 = value; Edges[0].v1 = value; } } public Vertex V2 { get { return Edges[2].v0; } set { if (value.MeshId != MeshId) throw new Exception("Not the same mesh"); Edges[2].v0 = value; Edges[1].v1 = value; } } public Triangle(int meshId, int index, int v0, int v1, int v2) { _index = index; _meshId = meshId; var edges = new Edge[3]; edges[0] = new Edge(meshId, index, v0, v1); edges[1] = new Edge(meshId, index, v1, v2); edges[2] = new Edge(meshId, index, v2, v0); _edges = edges; } } public struct Edge { public Vertex v0; public Vertex v1; private int _meshId; public int MeshId { get { return _meshId; } internal set { _meshId = value; } } private int _triangleIndex; public int TriangleIndex { get { return _triangleIndex; } internal set { _triangleIndex = value; } } public Edge(int meshId, int triangleIndex, int v0Index, int v1Index) { _meshId = meshId; _triangleIndex = triangleIndex; v0 = new Vertex() { MeshId = meshId, Index = v0Index }; v1 = new Vertex() { MeshId = meshId, Index = v1Index }; } } public struct Vertex { public int Index; private int _meshId; public int MeshId { get { return _meshId; } internal set { _meshId = value; } } public Vector3 position { get { return CustomMeshPool.GetMesh(_meshId).vertices[Index]; } set { CustomMeshPool.GetMesh(_meshId).vertices[Index] = value; } } public Vector3 normal { get { return CustomMeshPool.GetMesh(_meshId).normals[Index]; } set { CustomMeshPool.GetMesh(_meshId).normals[Index] = value; } } public Vector2 uv0 { get { return CustomMeshPool.GetMesh(_meshId).uv0[Index]; } set { CustomMeshPool.GetMesh(_meshId).uv0[Index] = value; } } public Vector2 uv2 { get { return CustomMeshPool.GetMesh(_meshId).uv2[Index]; } set { CustomMeshPool.GetMesh(_meshId).uv2[Index] = value; } } public Color color { get { return CustomMeshPool.GetMesh(_meshId).colors[Index]; } set { CustomMeshPool.GetMesh(_meshId).colors[Index] = value; } } }
Como você pode ver, o PLINQ é usado aqui. Isso ocorre porque os algoritmos de geometria computacional geralmente podem ser otimizados por meio de multithreading.
Obviamente, mais construções LINQ são criadas durante a execução de construções LINQ do que na execução de código “manual”. No entanto, essa desvantagem é amplamente compensada pela brevidade de tais projetos, bem como pela presença de ferramentas internas de gerenciamento de recursos no PLINQ. Além disso, a transição entre implementações de thread único e multi-thread é realizada com apenas um comando, o que facilita muito o processo de depuração.Torça, torça, eu quero confundir
Prosseguimos com as operações do movimento. Não há nada complicado em mover vértices. Só não se esqueça dos picos coincidentes: se necessário, sua posição também deve mudar.
O algoritmo é implementado adicionando um vetor de movimento à posição do vértice. A mudança ocorre em relação à origem do modelo (
pivô ). Vale a pena notar que a posição dos polígonos durante essas transformações pode mudar, mas as normais de seus vértices não podem. No entanto, para simplificar a apresentação, não consideraremos essa nuance.
As ferramentas CAD têm uma função para recalcular as normais, que geralmente são chamadas após a aplicação das transformações necessárias. Existem diferentes maneiras de fazer essa alocação. O mais comum calcula o normal ao plano de cada triângulo e, em seguida, atribui um normal a cada vértice como a média das normais dos triângulos aos quais esse vértice pertence.Em geral, não há boas razões para complicar o código e aplicar a matriz de transformação. O resultado da adição de um vetor de movimento à posição do vértice corresponde a uma ideia intuitiva de seu movimento.
| 
|
Listando métodos para mover um vértice public struct Vertex { ... public void Translate(Vector3 movement, bool withCoincident = false) { var newPosition = position + movement; if (withCoincident) { var vertices = CustomMeshPool.GetMesh(_meshId).vertices; var mask = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(position); for (int i = 0; i < vertices.Length; i++) if (mask[i]) vertices[i] = newPosition; } else { position = newPosition; } } } public class CustomMesh { … public bool[] GetVerticesInPosition(Vector3 position) { bool[] buffer = new bool[vertices.Length]; for (int i = 0; i < buffer.Length; i++) { buffer[i] = Mathf.Abs(position.x - vertices[i].x) < Mathf.Epsilon && Mathf.Abs(position.y - vertices[i].y) < Mathf.Epsilon && Mathf.Abs(position.z - vertices[i].z) < Mathf.Epsilon; } return buffer; } }
O movimento de arestas e triângulos é implementado da mesma maneira - adicionando um vetor de deslocamento.
Listando métodos para mover triângulos e arestas public struct Edge { … public void Translate(Vector3 movement, bool withCoincident = false) { if (withCoincident) { var vertices = CustomMeshPool.GetMesh(MeshId).vertices; var newV0Position = v0.position + movement; var newV1Position = v1.position + movement; var maskV0 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v0.position); var maskV1 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v1.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; } } else { v0.Translate(movement); v1.Translate(movement); } } } public struct Triangle { … public void Translate(Vector3 movement, bool withCoincident = false) { if (withCoincident) { var vertices = CustomMeshPool.GetMesh(_meshId).vertices; var newV0Position = V0.position + movement; var newV1Position = V1.position + movement; var newV2Position = V2.position + movement; var maskV0 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V0.position); var maskV1 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V1.position); var maskV2 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V2.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; else if (maskV2[i]) vertices[i] = newV2Position; } } else { V0.Translate(movement); V1.Translate(movement); V2.Translate(movement); } } }
Mas é mais conveniente girar e escalar usando
a matriz de transformação . O resultado dessas operações em relação à origem das coordenadas do modelo provavelmente não será o que você esperava ou queria ver. O ponto de referência de rotação e escala é geralmente considerado o meio do objeto - o mais compreensível para os seres humanos.
Listando métodos para rotacionar e dimensionar triângulos e arestas public struct Edge { … public void Rotate(Quaternion rotation, bool withCoincident = false) { var pivot = (v0.position + v1.position) * 0.5f; var matrix = Matrix4x4.TRS(pivot, rotation, Vector3.one); var newV0Position = matrix.MultiplyPoint(v0.position - pivot); var newV1Position = matrix.MultiplyPoint(v1.position - pivot); if (withCoincident) { var vertices = CustomMeshPool.GetMesh(MeshId).vertices; var maskV0 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v0.position); var maskV1 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v1.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; } } else { v0.position = newV0Position; v1.position = newV1Position; } } public void Scale(Vector3 scale, bool withCoincident = false) { var pivot = (v0.position + v1.position) * 0.5f; var matrix = Matrix4x4.TRS(pivot, Quaternion.identity, scale); var newV0Position = matrix.MultiplyPoint(v0.position - pivot); var newV1Position = matrix.MultiplyPoint(v1.position - pivot); if (withCoincident) { var vertices = CustomMeshPool.GetMesh(MeshId).vertices; var maskV0 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v0.position); var maskV1 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v1.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; } } else { v0.position = newV0Position; v1.position = newV1Position; } } } public struct Triangle { … public void Rotate(Quaternion rotation, bool withCoincident = false) { var pivot = (V0.position + V1.position + V2.position) / 3; var matrix = Matrix4x4.TRS(Vector3.zero, rotation, Vector3.one); var newV0Position = matrix.MultiplyPoint(V0.position - pivot) + pivot; var newV1Position = matrix.MultiplyPoint(V1.position - pivot) + pivot; var newV2Position = matrix.MultiplyPoint(V2.position - pivot) + pivot; if (withCoincident) { var vertices = CustomMeshPool.GetMesh(_meshId).vertices; var maskV0 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V0.position); var maskV1 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V1.position); var maskV2 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V2.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; else if (maskV2[i]) vertices[i] = newV2Position; } } else { Edges[0].v0.position = newV0Position; Edges[1].v0.position = newV1Position; Edges[2].v0.position = newV2Position; } Edges[0].v0.normal = matrix.MultiplyPoint(V0.normal); Edges[1].v0.normal = matrix.MultiplyPoint(V1.normal); Edges[2].v0.normal = matrix.MultiplyPoint(V2.normal); } public void Scale(Vector3 scale, bool withCoincident = false) { var pivot = (V0.position + V1.position + V2.position) / 3; var matrix = Matrix4x4.TRS(pivot, Quaternion.identity, scale); var newV0Position = matrix.MultiplyPoint(V0.position - pivot); var newV1Position = matrix.MultiplyPoint(V1.position - pivot); var newV2Position = matrix.MultiplyPoint(V2.position - pivot); if (withCoincident) { var vertices = CustomMeshPool.GetMesh(_meshId).vertices; var maskV0 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V0.position); var maskV1 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V1.position); var maskV2 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V2.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; else if (maskV2[i]) vertices[i] = newV2Position; } } else { Edges[0].v0.position = newV0Position; Edges[1].v0.position = newV1Position; Edges[2].v0.position = newV2Position; } } }
Enxame um buraco limpo para nós mesmos
Na modelagem 3D, uma operação de extrusão é frequentemente usada. Para sua implementação, o vetor de movimento (deslocamento) e o conjunto de polígonos devem ser conhecidos. O processo de extrusão pode ser decomposto em duas etapas:
1. O deslocamento dos polígonos por um determinado vetor de movimento (
deslocamento ). Nesse caso, é necessário duplicar os vértices separados por polígonos de contorno para não perturbar a posição dos elementos que não pertencem à parte deslocada. Em outras palavras, você precisa rasgar e mover a peça selecionada. Se esta etapa for concluída primeiro, o modelo provavelmente será dividido em partes que precisarão ser unidas no futuro.
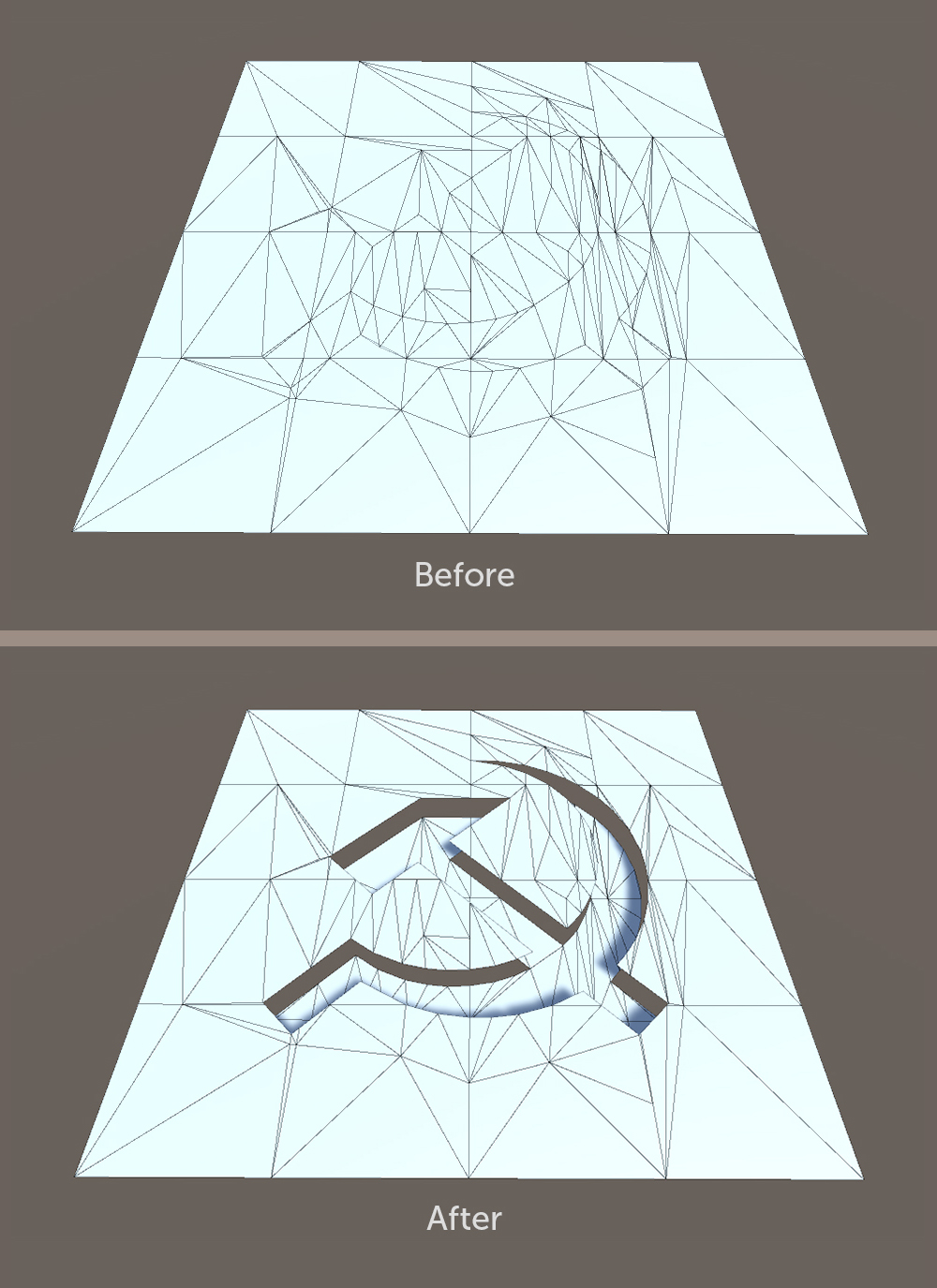
2. Adicionando nova geometria entre o limite da peça deslocada e o limite formado durante a extrusão. O espaço entre as partes principal e deslocada do modelo é preenchido com polígonos formando uma parede.
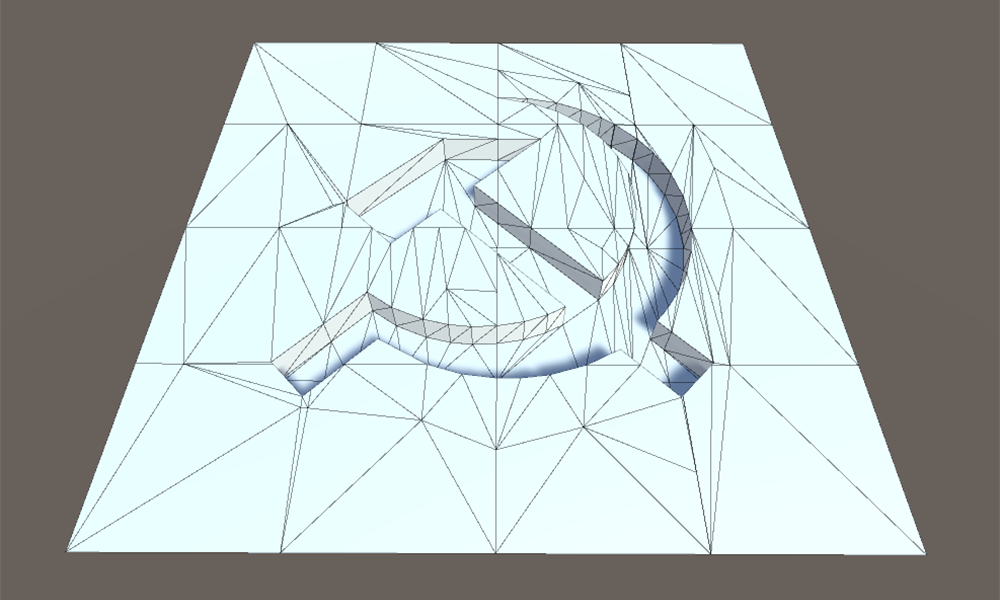
Na implementação, é mais conveniente construir primeiro o muro, porque antes do turno temos a posição inicial das bordas na borda e podemos usar esses dados imediatamente. Caso contrário, você teria que inverter a direção do vetor de cisalhamento ou salvar algumas das informações sobre o estado inicial da malha.
O modelo e suas partes com as quais trabalhamos são compostos de conjuntos de polígonos adjacentes aos pares (triângulos). Chamamos cada um desses conjuntos de
cluster .
Dois clusters dedicados no Blender
Primeiro, precisamos obter todas as arestas dos contornos que limitam os clusters selecionados. Para fazer isso, basta adicionar as arestas à lista sequencialmente. Se uma aresta correspondente for encontrada, ela deverá ser removida sem adicionar a atual. Para a operação correta de um algoritmo desse tipo, é necessário introduzir uma restrição: no conjunto selecionado de triângulos não existem mais que duas arestas coincidentes. Nos casos em que
Extrusão é usada, os modelos geralmente atendem a essa condição, e um algoritmo mais complexo requer grandes recursos computacionais.
Listando métodos para obter arestas pertencentes a contornos internal static class LinkedListExtension { internal static IEnumerable<LinkedListNode<T>> Nodes<T>(this LinkedList<T> list) { for (var node = list.First; node != null; node = node.Next) { yield return node; } } } public struct Vertex { … public bool IsInPosition(Vector3 other) { return Mathf.Abs(position.x - other.x) < Mathf.Epsilon && Mathf.Abs(position.y - other.y) < Mathf.Epsilon && Mathf.Abs(position.z - other.z) < Mathf.Epsilon; } } public struct Edge { … public bool Coincides(Edge other, bool includeDirection = false) { return v0.IsInPosition(other.v0.position) && v1.IsInPosition(other.v1.position) || !includeDirection && v1.IsInPosition(other.v0.position) && v0.IsInPosition(other.v1.position); } } public class CustomMesh { … private LinkedList<Edge> ObtainHullEdges(int[] triIndices) { var edges = new LinkedList<Edge>(); for (var i = 0; i < triIndices.Length; i++) { var edge = edges.Nodes().FirstOrDefault(e => e.Value.Coincides(Triangles[triIndices[i]].Edges[0])); if (edge != null) edges.Remove(edge); else edges.AddFirst(Triangles[triIndices[i]].Edges[0]); edge = edges.Nodes().FirstOrDefault(e => e.Value.Coincides(Triangles[triIndices[i]].Edges[1])); if (edge != null) edges.Remove(edge); else edges.AddFirst(Triangles[triIndices[i]].Edges[1]); edge = edges.Nodes().FirstOrDefault(e => e.Value.Coincides(Triangles[triIndices[i]].Edges[2])); if (edge != null) edges.Remove(edge); else edges.AddFirst(Triangles[triIndices[i]].Edges[2]); } return edges; } }
Depois de receber todas as bordas do contorno, você precisará construir as paredes correspondentes. Existem muitas opções de implementação, mas decidimos seguir o caminho de menor resistência - gerar paralelogramos na direção do vetor de movimento com base nas arestas separadamente. Como todos temos um deslocamento, como resultado dessa ação, os paralelogramos formarão uma parede sólida e fechada para cada cluster. Resta determinar a orientação dos elementos da parede.
A parede, como toda a malha, consiste em triângulos.
De acordo com a convenção do OpenGL , um triângulo destacado é renderizado na tela se, ao projetar seus pontos no plano da tela, contorná-los em ordem corresponder à caminhada no sentido horário:
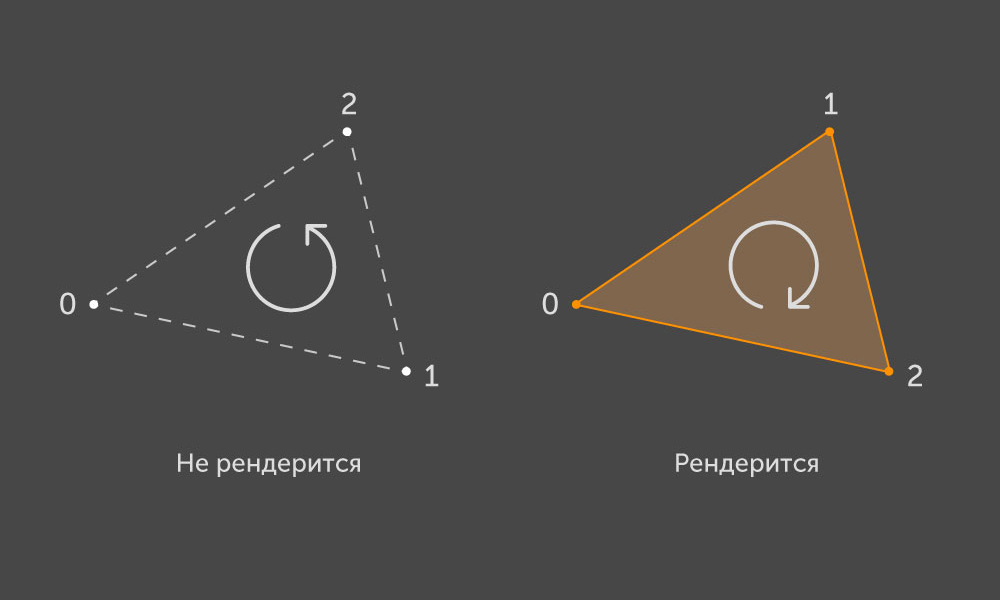
Portanto, um triângulo corresponde a um certo vetor normal que define o lado da frente. Cada triângulo é delimitado por um contorno convexo que consiste em três arestas. Cada aresta tem dois vértices representados em nossa estrutura como
v0 e
v1 . Definimos a direção da aresta para que
v0 seja o começo,
v1 seja o fim. Agora, se a direção das arestas do triângulo for definida de acordo com o desvio de seus vértices, qualquer contorno externo do cluster deverá ter um desvio no sentido horário ou anti-horário e qualquer interno - vice-versa. Implementamos os construtores
CustomMesh e
Triangle para que a travessia dos vértices de todos os triângulos corresponda à direção no sentido horário.
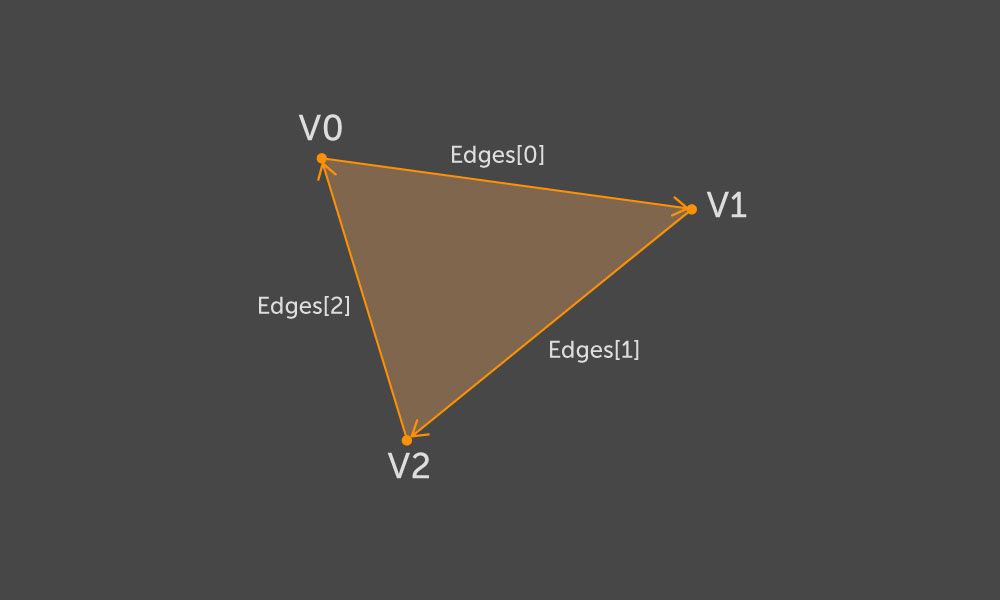
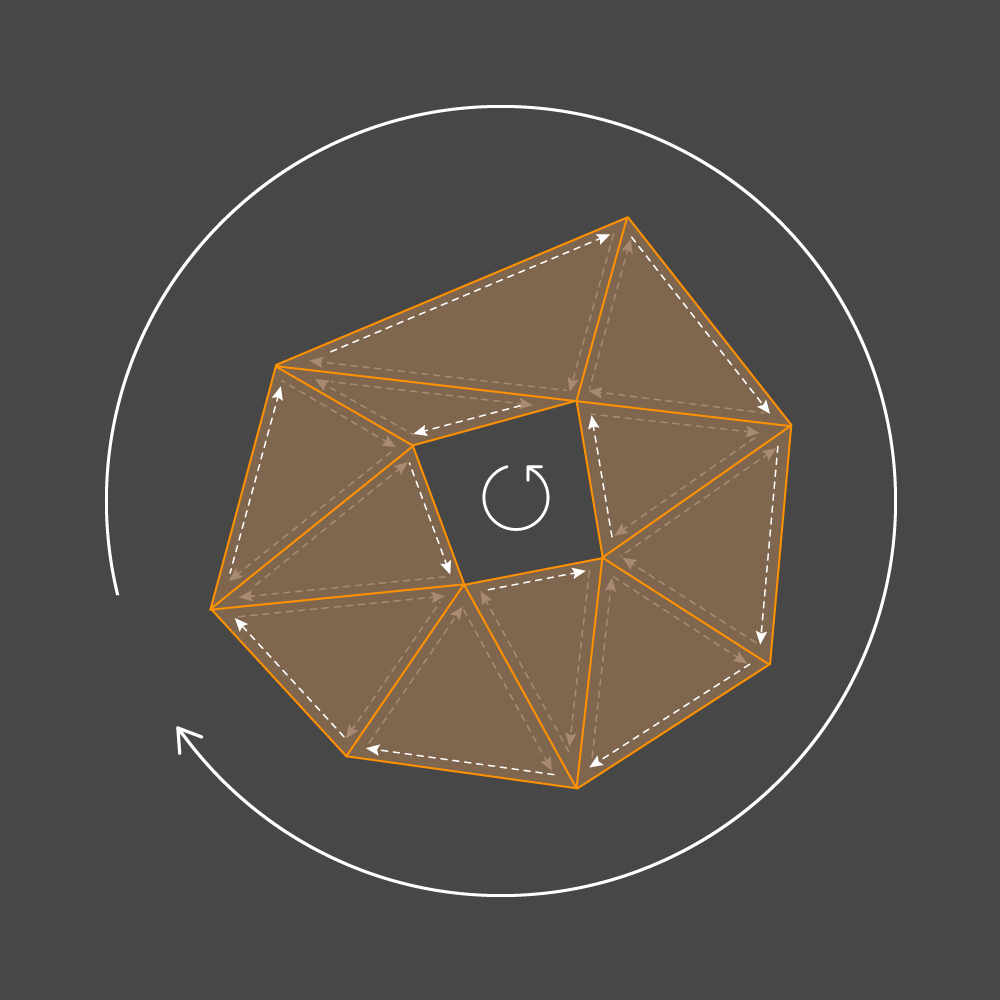
Tendo a direção de contornar o contorno, podemos dizer com certeza qual lado da nervura é a parte interna do contorno e qual é o externo. Com base nessas informações, escolheremos a orientação da parede. Seja (
v0, v1 ) a aresta com base na qual o paralelogramo desejado deve ser gerado. Tomamos os dois pontos
v2 e
v3 como as posições de deslocamento
v0 e
v1 . Então construímos dois triângulos de acordo com o seguinte esquema:
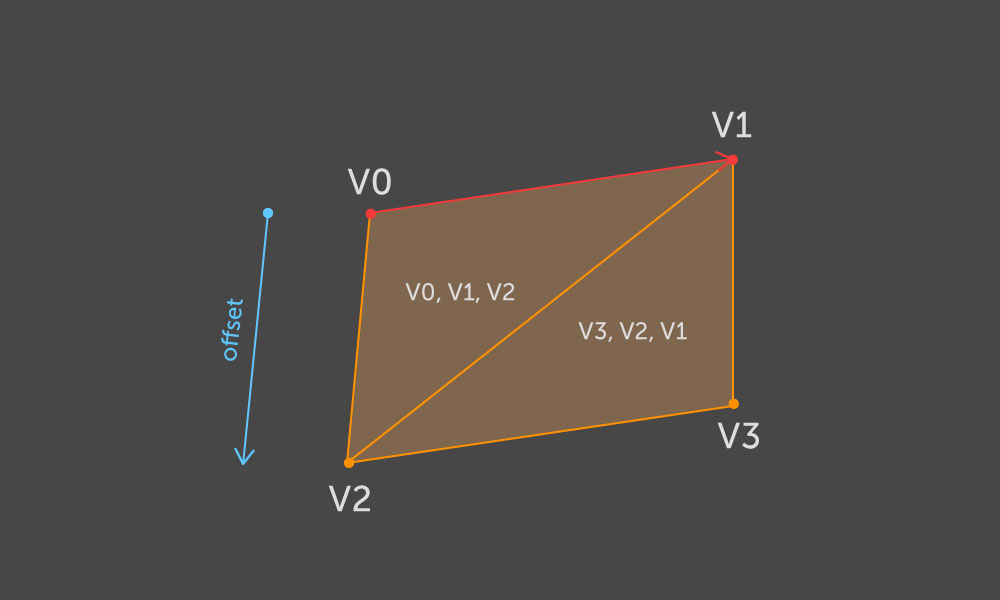
E assim para cada borda do contorno.
Listando um método para construir paredes usando uma lista de arestas public class CustomMesh { … private void ExtrudeEdgesSet(Edge[] edges, Vector3 offset) { if (offset == Vector3.zero || edges == null || edges.Length == 0) return; var initVerticesLength = vertices.Length; Array.Resize(ref vertices, initVerticesLength + edges.Length * 4); if (normals != null && normals.Length == initVerticesLength) { Array.Resize(ref normals, vertices.Length); } if (uv0 != null && uv0.Length == initVerticesLength) { Array.Resize(ref uv0, vertices.Length); } if (uv2 != null && uv2.Length == initVerticesLength) { Array.Resize(ref uv2, vertices.Length); } if (colors != null && colors.Length == initVerticesLength) { Array.Resize(ref colors, vertices.Length); } var initTrianglesLength = Triangles.Length; Array.Resize(ref Triangles, initTrianglesLength + edges.Length * 2); edges .AsParallel() .Select((edge, i) => { int j = initVerticesLength + i * 4; vertices[j] = edge.v0.position; vertices[j + 1] = edge.v1.position; vertices[j + 2] = edge.v0.position + offset; vertices[j + 3] = edge.v1.position + offset; if (normals != null && normals.Length == vertices.Length) { var normal = Vector3.Cross(vertices[j + 1] - vertices[j], offset); normals[j] = normals[j + 1] = normals[j + 2] = normals[j + 3] = normal; } if (uv0 != null && uv0.Length == vertices.Length) { uv0[j] = uv0[j + 2] = edge.v0.uv0; uv0[j + 1] = uv0[j + 3] = edge.v1.uv0; } if (uv2 != null && uv2.Length == vertices.Length) { uv2[j] = uv2[j + 2] = edge.v0.uv2; uv2[j + 1] = uv2[j + 3] = edge.v1.uv2; } if (colors != null && colors.Length == vertices.Length) { colors[j] = colors[j + 2] = edge.v0.color; colors[j + 1] = colors[j + 3] = edge.v1.color; } Triangles[initTrianglesLength + i * 2] = new Triangle( initTrianglesLength + i * 2, Id, j, j + 1, j + 2 ); Triangles[initTrianglesLength + i * 2 + 1] = new Triangle( initTrianglesLength + i * 2 + 1, Id, j + 3, j + 2, j + 1 ); return true; }).ToArray(); } }
Com essa abordagem, o lado frontal das paredes geradas estará correto para os slides e para os poços. Há apenas uma limitação significativa: o conjunto de triângulos sobre os quais a operação de
extrusão é realizada não deve ser enrolado em torno de si com relação ao vetor de movimento.
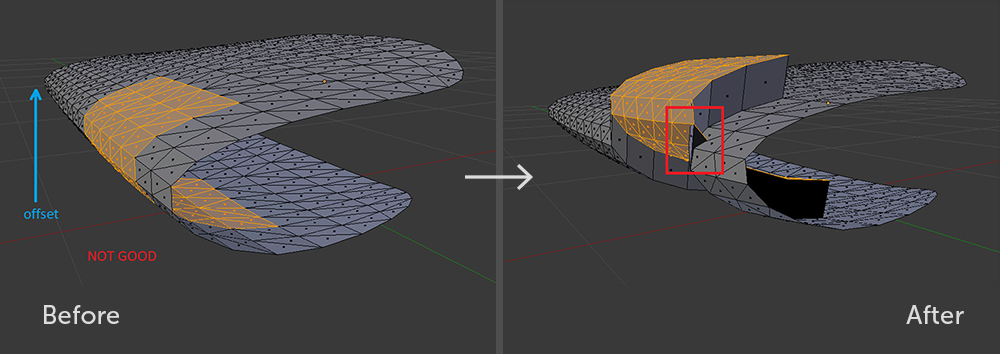Um subconjunto de polígonos inválido em relação ao deslocamento. Mesmo no Blender com essa extrusão, não será possível evitar uma curva geométrica.
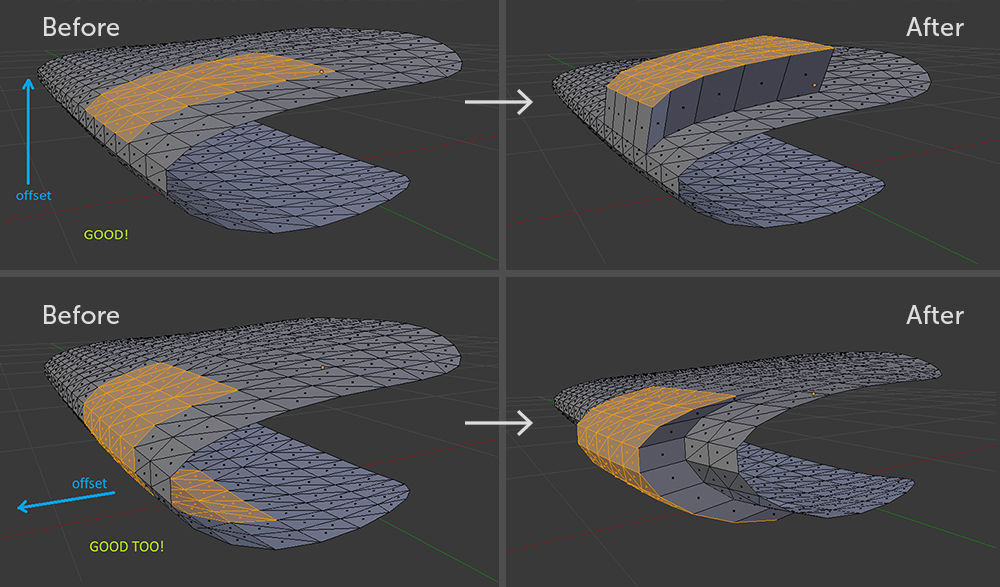Subconjuntos válidos de polígonosA parede está pronta, resta mudar os triângulos. Esta etapa do algoritmo é fácil de entender, embora a implementação tenha sido complicada.
No nosso caso, precisamos garantir que cada vértice do cluster pertença apenas aos seus triângulos. Se a condição não for atendida, alguns polígonos vizinhos poderão alcançar o cluster. A solução para essa situação é duplicar cada vértice que pertence ao cluster e ao restante do modelo. Em seguida, para todos os polígonos no cluster, substitua o índice desse vértice pelo índice duplicado. Quando a condição é satisfeita, movemos todos os vértices do cluster para o vetor de movimento.
Listando um método para mudar um cluster de polígonos public class CustomMesh { … private void TranslateTrianglesHard(int[] triIndices, Vector3 offset, int[] hullVerts) { var newVertexIndices = new Dictionary<int, int>(); var initVerticesCount = vertices.Length; Triangles.Where((t, i) => !triIndices.Contains(i)).Select(t => { if (hullVerts.Contains(t.V0.Index) && !newVertexIndices.ContainsKey(t.V0.Index)) newVertexIndices.Add(t.V0.Index, initVerticesCount + newVertexIndices.Count); if (hullVerts.Contains(t.V1.Index) && !newVertexIndices.ContainsKey(t.V1.Index)) newVertexIndices.Add(t.V1.Index, initVerticesCount + newVertexIndices.Count); if (hullVerts.Contains(t.V2.Index) && !newVertexIndices.ContainsKey(t.V2.Index)) newVertexIndices.Add(t.V2.Index, initVerticesCount + newVertexIndices.Count); return false; }).ToArray(); Array.Resize(ref vertices, initVerticesCount + newVertexIndices.Count); foreach (var pair in newVertexIndices) vertices[pair.Value] = vertices[pair.Key] + offset; if (normals != null && normals.Length == initVerticesCount) { Array.Resize(ref normals, vertices.Length); foreach (var pair in newVertexIndices) normals[pair.Value] = normals[pair.Key]; } if (uv0 != null && uv0.Length == initVerticesCount) { Array.Resize(ref uv0, vertices.Length); foreach (var pair in newVertexIndices) uv0[pair.Value] = uv0[pair.Key]; } if (uv2 != null && uv2.Length == initVerticesCount) { Array.Resize(ref uv2, vertices.Length); foreach (var pair in newVertexIndices) uv2[pair.Value] = uv2[pair.Key]; } if (colors != null && colors.Length == initVerticesCount) { Array.Resize(ref colors, vertices.Length); foreach (var pair in newVertexIndices) colors[pair.Value] = colors[pair.Key]; } var alreadyMoved = new HashSet<int>(); for (var i = 0; i < triIndices.Length; i++) { if (newVertexIndices.ContainsKey(Triangles[triIndices[i]].V0.Index)) { var index = newVertexIndices[Triangles[triIndices[i]].V0.Index]; Triangles[triIndices[i]].Edges[0].v0.Index = index; Triangles[triIndices[i]].Edges[2].v1.Index = index; } else if (!alreadyMoved.Contains(Triangles[triIndices[i]].V0.Index)) { vertices[Triangles[triIndices[i]].V0.Index] += offset; alreadyMoved.Add(Triangles[triIndices[i]].V0.Index); } if (newVertexIndices.ContainsKey(Triangles[triIndices[i]].V1.Index)) { var index = newVertexIndices[Triangles[triIndices[i]].V1.Index]; Triangles[triIndices[i]].Edges[0].v1.Index = index; Triangles[triIndices[i]].Edges[1].v0.Index = index; } else if (!alreadyMoved.Contains(Triangles[triIndices[i]].V1.Index)) { vertices[Triangles[triIndices[i]].V1.Index] += offset; alreadyMoved.Add(Triangles[triIndices[i]].V1.Index); } if (newVertexIndices.ContainsKey(Triangles[triIndices[i]].V2.Index)) { var index = newVertexIndices[Triangles[triIndices[i]].V2.Index]; Triangles[triIndices[i]].Edges[1].v1.Index = index; Triangles[triIndices[i]].Edges[2].v0.Index = index; } else if (!alreadyMoved.Contains(Triangles[triIndices[i]].V2.Index)) { vertices[Triangles[triIndices[i]].V2.Index] += offset; alreadyMoved.Add(Triangles[triIndices[i]].V2.Index); } } } }
Feito. Agora, somando os resultados de todas as etapas, temos um buraco ou uma colina.
Listando o método final para a operação Extrude public class CustomMesh { … public void ExtrudeTriangles(int[] triIndices, Vector3 offset) { var edges = ObtainHullEdges(triIndices); ExtrudeEdgesSet(edges.ToArray(), offset); var hullVertices = edges.Select(edge => edge.v0.Index).ToArray(); TranslateTrianglesHard(triIndices, offset, hullVertices); } }
Tendo brincado com as coordenadas da varredura de textura e o deslocamento dos pontos de contorno, você pode obter um recesso:
E isso não é tudo
Além das operações de edição discutidas acima, também usamos outros métodos convenientes para trabalhar com modelos.
Por exemplo, também escrevemos o método
Combine () para combinar dois
CustomMesh . A principal diferença entre nossa implementação e
UnityEngine.Mesh.CombineMeshes () é que, se alguns vértices são completamente equivalentes ao combinar as malhas, deixamos apenas um deles, evitando assim geometrias desnecessárias.
No mesmo módulo, implementamos
o algoritmo de triangulação no plano de Delaunay . Usando-o, você pode, por exemplo, fechar um grande buraco criado usando
Extrude com uma tampa plana com textura de água e obter um lago:
Bem, resolvi isso! No próximo artigo, consideraremos os recursos de importação de
.fbx para o
Unity e os métodos de validação de modelo em um projeto.
Para um lanche (apenas para lulz)