O quarto nível do multi-universo de Max Tegmark

Há quase dez anos, li um artigo de Max Tegmark , um brilhante físico e filósofo, e encontrei nele as respostas para muitas perguntas que me atormentaram a vida toda. O artigo é incrível, por dois meses fiquei com a impressão de que era. Infelizmente, isso é Longrid, e também em inglês. Portanto, decidi nem mesmo traduzi-la - a tradução ainda seria muito longa para Habr, mas pelo menos expus a idéia principal na ordem que me parece lógica e removendo detalhes desnecessários (Max, perdoe-me!)

Fórmulas e Bagagem

$$

$$A = bc$$

O que é isso É improvável que esta fórmula lhe diga algo. E se eu escrever assim:

$$

$$F = ma$$

Então você reconhecerá imediatamente a lei de Newton. Naturalmente, ambas as fórmulas são equivalentes, estamos acostumados ao fato de que a força é denotada por F, massa m, além disso, queremos dizer que a matéria ocorre no espaço tridimensional, que os corpos têm coordenadas etc. Ou seja, a teoria tem dois componentes: fórmulas e blá blá ao seu redor. Max chama o segundo componente de bagagem verbal .

Considere a árvore das teorias existentes:



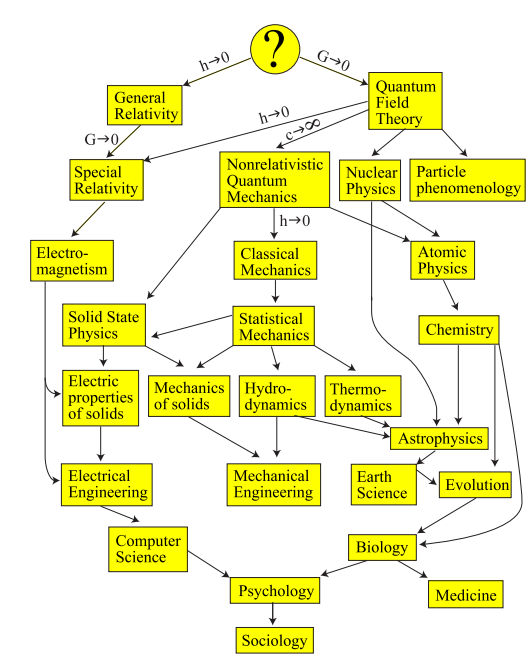
No fundo, está a sociologia, onde quase não existem fórmulas, mas muitas palavras. Subindo as escadas, encontramos uma matemática cada vez mais complicada. Mas com as palavras, está ficando cada vez pior: tente descobrir de um cientista que está envolvido na física fundamental que horas são. É óbvio para você que o tempo é uma sequência de eventos e flui para a frente . Quanto mais você sabe e quanto mais fundo, menos óbvio se torna. A descrição de que horas é, desmorona cada vez mais com o fato de que o tempo é a letra t , que está envolvida em tais e tais equações.

Então Max percebe que:
À medida que você passa para um nível cada vez mais fundamental, a matemática se torna mais complexa e a bagagem começa a degenerar cada vez mais. No limite, sugere Max, o TOE (Teoria de Tudo - Teoria Geral de Tudo) não tem bagagem . Portanto, o TOE consiste apenas em fórmulas .

Este é o primeiro ingrediente. Lembre-se dele.

Física “Pelo contrário”

Como isso é possível? A física está tentando encontrar equações para o nosso mundo, com base em observações e dados experimentais. Max sugere olhar para " Física do zero " , " Física do zero " , você pergunta a equação: que tipo de mundo você obtém?

Podemos definir as leis do mundo ... bem, por exemplo, o jogo "vida". Podemos fazer sem uma descrição verbal? Como, por exemplo, dizer que o espaço das células é bidimensional? Por meio de equações, indicando uma lei da potência, com que rapidez o número de células cresce além da distância N. Outro exemplo, as equações da teoria das cordas convergem apenas se a dimensão do espaço for 10, 11 ou 26. Talvez, a princípio, formular física pareça axiomaticamente difícil, mas os matemáticos tiveram sucesso. criando teorias axiomáticas (e mundos). Tomemos, por exemplo, os axiomatics do Peano . Essas são fórmulas puras: não explicam o que é um "número", o que significa somar ou multiplicar.

Descrição vs Equivalência.

O que nós temos? Temos (será) um TOE descrevendo tudo o que existe.
Um segundo ... E o que significa "descrever"? Por exemplo, a mecânica descreve o movimento dos corpos. Mas sabemos que tudo isso é possível graças a várias simplificações: os corpos não são pontos materiais, há resistência do ar, atrito etc. Existem fórmulas que descrevem a realidade, mas sabemos que o mundo real é diferente do ideal, descrito por fórmulas.

Mas, no caso do TOE, não é assim: qualquer aspecto absolutamente físico da realidade é descrito por fórmulas - ou não é TOE. Qual é a diferença entre teoria e realidade neste caso, se forem absolutamente equivalentes?

Max argumenta que, no caso do TOE, a matemática não descreve a realidade, e a matemática é a realidade . Se você discordar repentinamente, o oposto significaria que existem equações com suas soluções, existe exatamente o mesmo mundo que está completamente sujeito às fórmulas indicadas, mas também reais . Nesse caso, as palavras “ ainda reais ” são bagagem verbal em sua forma pura, que abandonamos acima, uma anima sola moderna da física. Assim, somos forçados a admitir que, no nível fundamental, física e matemática são a mesma coisa.

Fórmulas e chamas

Max não foi o primeiro a ter essas idéias. O próprio Hawking fez a pergunta: " Mas o que exatamente a chama respira nessas equações, criando o universo?" " " O que lança fogo nas equações e cria um universo para elas descreverem? "



Se disséssemos que o nosso universo é especial porque existe , voltaríamos a dar um passo atrás no conceito de anima sola. Não, nada sopra a chama em nossas fórmulas. Seria estranho se todos os sistemas axiomáticos da matemática fossem divididos em duas classes desiguais: sistemas para os quais existem universos e sistemas para azar. Isso contradiz toda a hipótese do universo matemático.

Tudo isso pode ser explicado apenas desta maneira: se não houver anima sola, todos os sistemas axiomáticos são iguais e o universo corresponde a cada sistema axiomático. Sim, a maioria dos sistemas é provavelmente trivial, e talvez a maioria dos axiomatics não dê a oportunidade de desenvolver (isto é, aparecer em soluções) sistemas complexos, não triviais e, principalmente, vida.

"Física vice-versa" ainda aguarda seus futuros pesquisadores. Eu daria muito carinho para descobrir se o nosso universo é o mais simples daqueles onde a vida inteligente é possível ou não.

Respostas a algumas perguntas

Curiosamente, após o primeiro passo (o TOU não tem bagagem), o segundo passo (matemática e física são a mesma coisa) e o terceiro passo (cada axiomatics cria um universo) foram forçados. Foi assim que chegamos.

E por que o universo existe?
Resposta: porque pode existir.

Quando essas estruturas surgiram e por que surgiram?

Estruturas matemáticas não existem no tempo e no espaço. Eles simplesmente existem.

Somos uma emulação?

Não. Para a existência de estruturas matemáticas, nenhuma máquina é necessária para “contá-las”. O número 19 é simples, independentemente de haver ou não um computador que o tempo todo tenta dividi-lo em um ciclo, verificando a simplicidade

E isso geralmente é como ciência ou fantasias?

Como podemos postular algo que não podemos verificar fundamentalmente? Max espera essa crítica. De fato, não é a primeira vez que fazemos isso. Há muito que estamos acostumados ao conceito de multiverso.



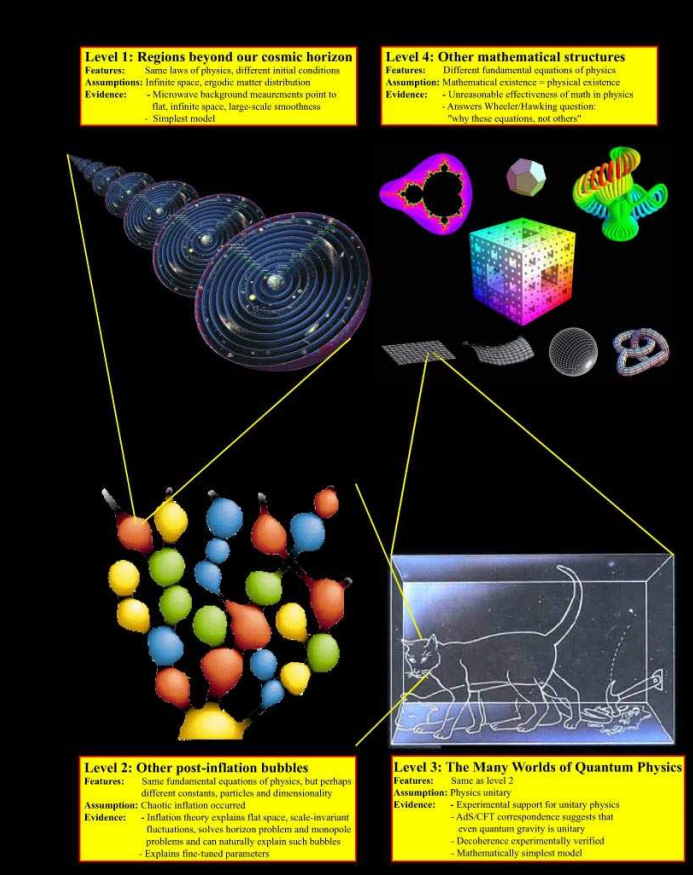No nível 1, estamos falando de áreas do universo que estão se afastando tão rapidamente de nós devido à expansão que elas nunca mais serão causalmente conectadas conosco. No entanto, nem um único cosmologista virará a língua para dizer que não há nada lá, porque não podemos voar para lá.

No nível 2, estamos falando de outras "bolhas" na teoria da inflação eterna, onde, talvez, sob as mesmas leis da física, outras condições iniciais e outras constantes físicas

O nível 3 é formado pelos universos alternativos do Multiverso, interpretados por Everett . Este será um artigo separado.



Somos forçados a aceitar a existência do nível 4 , correspondente a outros universos matemáticos que ainda precisamos estudar (teoricamente).