Como o erro se transforma em pecado

Uma lenda urbana diz que o criador de saquetas de açúcar, paus, se enforcou quando soube que os consumidores não os quebram ao meio por um copo, mas arrancam delicadamente a ponta. Isso, é claro, não é assim, mas se essa lógica for seguida, um amante da cerveja britânica Guinness chamado William Gosset não deve se enforcar, mas sua rotação no caixão já deve perfurar a Terra até o centro. E tudo porque sua invenção icônica, publicada sob o pseudônimo de Student , foi desastrosamente usada por décadas.

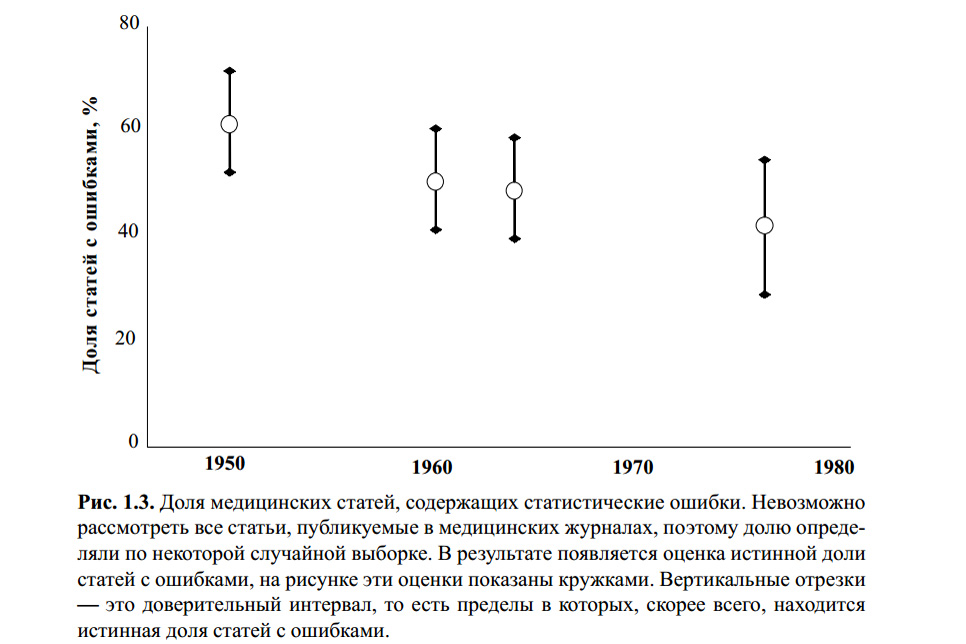
A figura acima é do livro de S. Glanz. Estatística biomédica. Per. do inglês - M., Practice, 1998 - 459 p. Não sei se alguém verificou erros estatísticos nos cálculos deste gráfico. No entanto, vários artigos modernos sobre o tema e minha própria experiência indicam que o critério t de Student permanece o mais famoso e, portanto, o mais popular em uso, com ou sem.

A razão para isso é a educação superficial (professores rigorosos ensinam que você precisa "verificar estatísticas", caso contrário, uuuuuu!), Facilidade de uso (tabelas e calculadoras on-line estão disponíveis em abundância) e uma relutância banal em se aprofundar no fato de que "e assim funciona". A maioria das pessoas que usou esse critério pelo menos uma vez em seu trabalho final ou mesmo em trabalho científico diz algo como: "Bem, comparamos 5 crianças em idade escolar com raiva e 7 jogadores em idade escolar em termos de agressão, nosso valor na mesa se aproxima de p = 0,05 e isso significa que os jogos são ruins. Bem, sim, não exatamente, mas com uma probabilidade de 95%. " Quantos erros lógicos e metodológicos eles cometeram?

O básico

Em que se baseia o teste t do aluno? A lógica é retirada do teorema bayesiano, a base matemática é da distribuição gaussiana, a metodologia é baseada na análise de variância:

onde o parâmetro μ é a expectativa matemática (valor médio) da distribuição e o parâmetro σ é o desvio padrão (σ ² é a variação) da distribuição.

O que é análise de variância? Imagine um público Habr, classificado pelo número de pessoas de cada idade. É provável que o número de pessoas por idade obedeça à distribuição normal - de acordo com a função de Gauss:

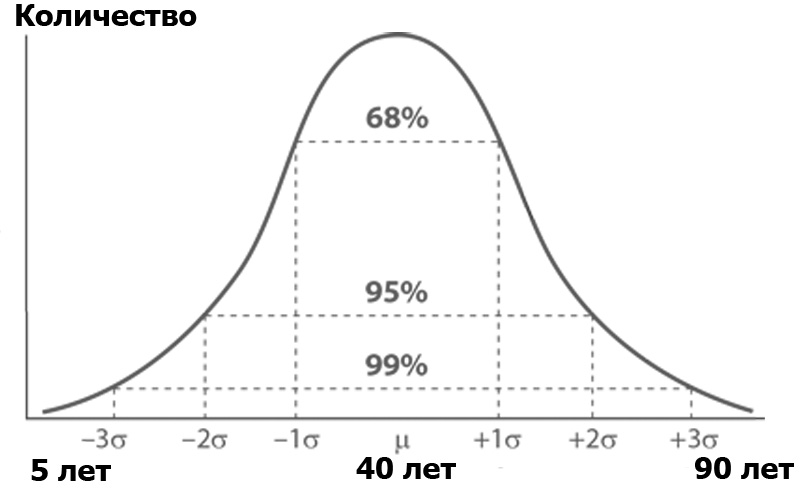
A distribuição normal tem uma propriedade interessante - quase todos os seus valores estão no limite de três desvios-padrão do valor médio. E qual é o desvio padrão? Essa é a raiz da variação. A dispersão , por sua vez, é a soma dos quadrados da diferença de todos os membros da população em geral e o valor médio dividido pelo número desses membros:

$$

$$σ_ {n} ^ {2} = {\ frac {1} {n}} \ soma \ limites _ {{i = 1}} ^ {n} \ esquerda (X_ {i} - {\ bar {X} } \ direita) ^ {2}$$

Ou seja, cada valor foi subtraído da média, elevado ao quadrado para matar os menos e, em seguida, calculou a média, estupidamente resumida e dividida pelo número desses valores. O resultado é uma medida da dispersão média dos valores em relação à variação média.

Imagine que selecionamos duas amostras nessa população em geral : leitores do hub de criptomoeda e leitores do hub de ferro antigo. Ao fazer uma amostra aleatória , sempre obtemos distribuições próximas do normal . E agora conseguimos um pequeno distribuidor em nossa população:

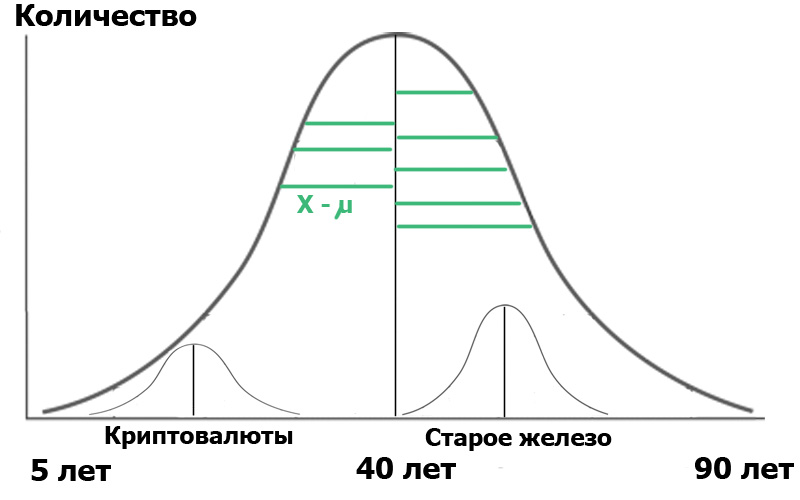
Para maior clareza, mostrei segmentos verdes - a distância dos pontos de distribuição ao valor médio. Se os comprimentos desses segmentos verdes forem elevados ao quadrado, somados e calculados a média - esta será a variação.

E agora - atenção. Podemos caracterizar a população através dessas duas pequenas amostras. Por um lado, as variações das amostras caracterizam a variação de toda a população. Por outro lado, os valores médios das próprias amostras também são números para os quais a variação pode ser calculada! Então: temos a média das variações das amostras e a variação dos valores médios das amostras.

Então, podemos realizar a análise de variância, representando-a aproximadamente na forma de uma fórmula lógica:

$$

$$F = {\ frac {variação \: populações \: por \: média \: valores \: amostras} {variação \: populações \: por \: variações \: amostras}}$$

O que a fórmula acima nos dará? Muito simples Nas estatísticas, tudo começa com a "hipótese nula", que pode ser formulada como "parecia-nos", "todas as coincidências são aleatórias" - no sentido de "e" não há conexão entre os dois eventos observados "- se estritamente. Portanto, no nosso caso, a hipótese nula seria a ausência de diferenças significativas entre a distribuição etária de nossos usuários em dois hubs. No caso da hipótese nula, nosso diagrama será mais ou menos assim:

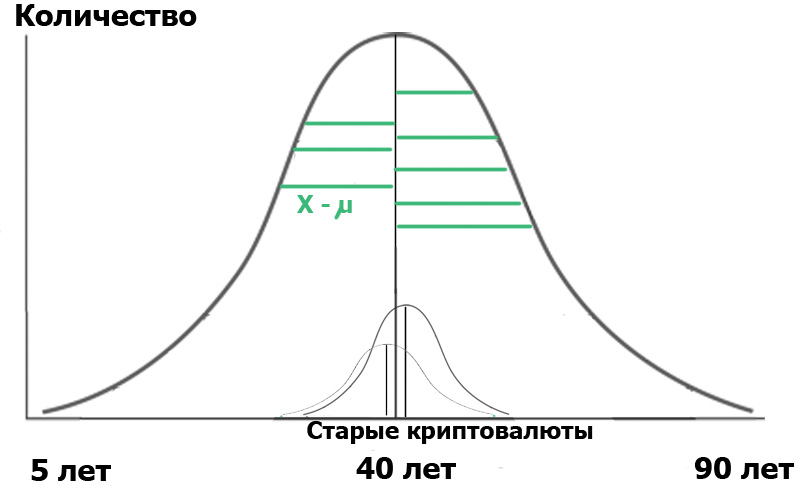
Isso significa que tanto as variações das amostras quanto seus valores médios são muito próximas ou iguais entre si e, portanto, falando de maneira geral, nosso critério

$$

$$F = {\ frac {variação \: populações \: por \: média \: valores \: amostras} {variação \: populações \: por \: variações \: amostras}} = 1$$

Mas se as variações das amostras forem iguais, mas as idades dos habrausers forem realmente muito diferentes, o numerador (variação dos valores médios) será grande e F será muito mais que a unidade. Em seguida, o diagrama será mais parecido na figura anterior. E o que isso nos dará? Nada, se você não prestar atenção à redação: a hipótese nula seria a ausência de diferenças significativas .

Mas o significado ... nós o definimos. É denotado como α e tem o seguinte significado: o nível de significância é a probabilidade máxima aceitável de rejeitar erroneamente a hipótese nula . Em outras palavras, consideraremos nosso evento como uma diferença significativa entre um grupo e outro, apenas se a probabilidade P de nosso erro for menor que α. Esse é o notório p <0,05, porque geralmente na pesquisa biomédica o nível de significância é de 5%.

Bem, então tudo é simples. Dependendo de α, existem valores críticos de F, começando com o qual rejeitamos a hipótese nula. Eles são emitidos na forma de tabelas, às quais estamos tão acostumados a usar. Isto é para análise de variância. E o aluno?

Então disse o aluno

E o critério do aluno é apenas um caso especial de análise de variância. Novamente, não sobrecarregarei você com fórmulas que são facilmente do Google, mas transmitirei a essência:

$$

$$t = {\ frac {diferença \: média \: valores \: amostras} {padrão \: erro \: diferenças \: amostra \: média}}$$

Portanto, toda essa longa explicação precisava ser muito rude e fluente, mas mostra claramente em que o critério t se baseia. E, consequentemente, de quais de suas propriedades inerentes seguem diretamente as limitações de seu uso, sobre as quais até cientistas profissionais cometem erros com tanta frequência.

Propriedade um: normalidade da distribuição.

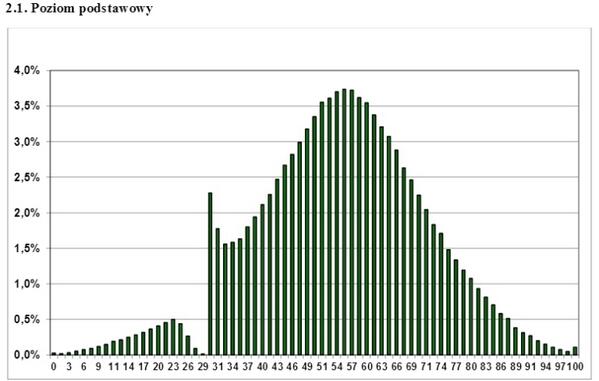
Este é um par de anos como um gráfico da distribuição das notas dos exames estatais poloneses na Internet. Que conclusão pode ser tirada disso? Que este exame não é aprovado apenas Gopnik completamente repelido? Quais professores "alcançam" os alunos? Não, apenas um - para uma distribuição diferente da normal, você não pode aplicar critérios de análise paramétrica, como Aluno. Se você possui um gráfico de distribuição unilateral, serrilhado, ondulado e discreto - esqueça o critério t, não poderá usá-lo. No entanto, isso às vezes é ignorado com sucesso, mesmo por um trabalho científico sério.

O que fazer neste caso? Use o chamado critério de análise não paramétrica. Eles implementam uma abordagem diferente, ou seja, dados de classificação, ou seja, afastando-se dos valores de cada um dos pontos para a classificação atribuída a ele. Esses critérios são menos precisos que os paramétricos, mas pelo menos seu uso é correto, em contraste com o uso injustificado do critério paramétrico em uma população anormal. Desses critérios, o critério U de Mann-Whitney é mais conhecido e, freqüentemente, é usado como critério "para uma amostra pequena". Sim, ele permite lidar com amostras de até 5 pontos, mas esse, como já deve estar claro, não é seu principal objetivo.

A segunda propriedade: você se lembra da fórmula? Os valores do critério F mudaram com a diferença (variação maior) dos valores médios das amostras . Mas o denominador, isto é, as próprias variações, não deve mudar. Portanto, outro critério de aplicabilidade deve ser a igualdade de variâncias. O fato de essa verificação ser observada com menos frequência é dito, por exemplo, aqui: Erros na análise estatística de dados biomédicos. Leonov V.P. International Journal of Medical Practice, 2007, n. 2, pp . 19-35 .

Propriedade três: comparação de duas amostras. Eles gostam de usar o critério t para comparar mais de dois grupos. Isso geralmente é feito da seguinte maneira: as diferenças entre o grupo A de B, B de C e A de C. são comparadas em pares.Em seguida, com base nisso, é feita uma certa conclusão, que é absolutamente incorreta. Nesse caso, surge o efeito de múltiplas comparações.
Tendo obtido um valor suficientemente alto de t em qualquer uma das três comparações, os pesquisadores relatam que "P <0,05". Mas, de fato, a probabilidade de erro excede significativamente 5%.

Porque

Descobrimos: por exemplo, o estudo adotou um nível de significância de 5%. Isso significa que a probabilidade máxima aceitável de rejeitar erroneamente a hipótese nula ao comparar os grupos A e B é de 5%. Parece que tudo está correto? Mas o mesmo erro exato ocorrerá no caso de comparar os grupos B e C, e ao comparar os grupos A e C também. Consequentemente, a probabilidade de cometer um erro como um todo com esse tipo de avaliação não será de 5%, mas de muito mais. Em geral, essa probabilidade é igual a
P ′ = 1 - (1 - 0,05) ^ k
onde k é o número de comparações.

Então, em nosso estudo, a probabilidade de cometer um erro ao rejeitar a hipótese nula é de aproximadamente 15%. Ao comparar os quatro grupos, o número de pares e, consequentemente, as possíveis comparações pareadas é 6. Portanto, com um nível de significância em cada uma das comparações de 0,05
a probabilidade de detectar erroneamente uma diferença em pelo menos um não é mais 0,05, mas 0,31.

Ainda assim, este erro não é difícil de eliminar. Uma maneira é introduzir a emenda de Bonferroni. A desigualdade de Bonferroni nos diz que se você aplicar os critérios k vezes
com um nível de significância de α, a probabilidade, em pelo menos um caso, de encontrar uma diferença onde ela não existe não excede o produto de k por α. A partir daqui:
α ′ <αk,
onde α 'é a probabilidade de, pelo menos uma vez, confundir as diferenças. Então, nosso problema é resolvido com muita simplicidade: precisamos dividir nosso nível de significância pela correção de Bonferroni - isto é, pela multiplicidade de comparações. Para três comparações, precisamos pegar os valores correspondentes a α = 0,05 / 3 = 0,0167 das tabelas de teste t. Repito: é muito simples, mas esta alteração não pode ser ignorada. A propósito, você não deve se deixar levar por essa emenda, mesmo depois de dividir por 8, os valores do critério t são desnecessariamente mais rígidos.

Em seguida, vêm as "pequenas coisas" que muitas vezes nem percebem. Deliberadamente, não forneço fórmulas aqui para não reduzir a legibilidade do texto, mas lembre-se de que os cálculos do teste t variam nos seguintes casos:

• Tamanhos diferentes de duas amostras (em geral, lembre-se de que, no caso geral, comparamos dois grupos usando a fórmula para o critério de duas amostras);

  
  

• Disponibilidade de amostras dependentes. São casos em que os dados são medidos de um paciente em diferentes intervalos de tempo, dados de um grupo de animais antes e depois do experimento, etc.

  
  

Finalmente, para que você possa imaginar toda a extensão do que está acontecendo, fornecerei dados mais recentes sobre o uso incorreto do critério t. Os números são de 1998 e 2008 para várias revistas científicas chinesas e falam por si. Eu realmente quero que isso se torne mais descuidado em design do que dados científicos imprecisos:

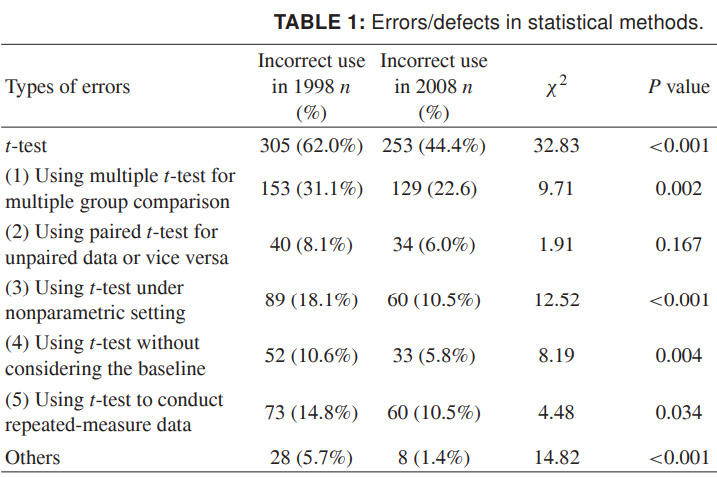
Fonte: Uso indevido de métodos estatísticos em 10 principais revistas médicas chinesas em 1998 e 2008. Shunquan Wu et al, The Scientific World Journal, 2011, 11, 2106-2114

Lembre-se de que o baixo significado dos resultados não é tão triste quanto um resultado falso. É impossível levar ao pecado científico - conclusões falsas - distorcendo os dados com estatísticas aplicadas incorretamente.

Sobre a interpretação lógica, inclusive incorreta, dos dados estatísticos, talvez eu conte separadamente.

Leia direito.