Carro de montanha: resolvendo o desafio clássico com treinamento de reforço

Como regra, modificações em algoritmos que dependem dos recursos específicos de uma tarefa específica são consideradas menos valiosas, pois são difíceis de generalizar para uma classe mais ampla de problemas. No entanto, isso não significa que essas modificações não sejam necessárias. Além disso, muitas vezes eles podem melhorar significativamente o resultado, mesmo para problemas clássicos simples, o que é muito importante na aplicação prática de algoritmos. Como exemplo, neste post, vou resolver o problema do Mountain Car com treinamento de reforço e mostrar que, usando o conhecimento de como a tarefa é organizada, ela pode ser resolvida muito mais rapidamente.

Sobre mim

Meu nome é Oleg Svidchenko, agora estou estudando na Escola de Ciências Físicas, Matemáticas e da Computação do HSE de São Petersburgo, antes de estudar na Universidade de São Petersburgo por três anos. Também trabalho na JetBrains Research como pesquisador. Antes de entrar na universidade, estudei no SSC da Universidade Estadual de Moscou e me tornei o vencedor da Olimpíada de toda a Rússia de crianças em idade escolar em ciência da computação, como parte da equipe de Moscou.

Do que precisamos?

Se você estiver interessado em experimentar o treinamento de reforço, o desafio do Mountain Car é ótimo para isso. Hoje, precisamos do Python com as bibliotecas Gym e PyTorch instaladas, além do conhecimento básico de redes neurais.

Descrição da tarefa

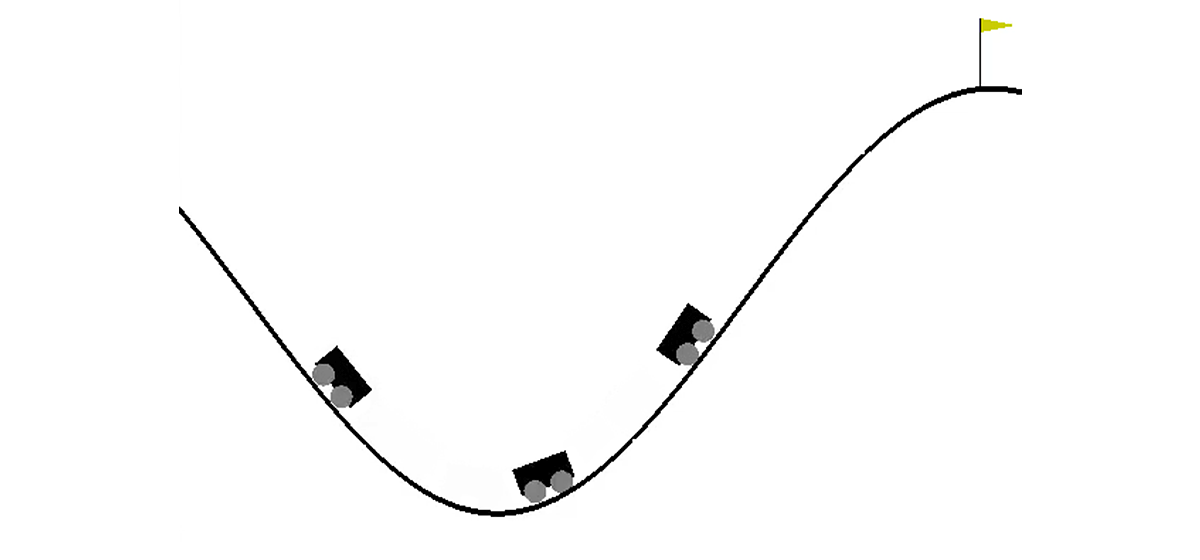
Em um mundo bidimensional, um carro precisa subir do buraco entre duas colinas até o topo da colina direita. É complicado pelo fato de ela não ter força de motor suficiente para superar a força da gravidade e entrar na primeira tentativa. Somos convidados a treinar um agente (no nosso caso, uma rede neural), que pode, controlando-a, subir a ladeira direita o mais rápido possível.

O controle da máquina é realizado através da interação com o ambiente. É dividido em episódios independentes, e cada episódio é realizado passo a passo. Em cada etapa, o agente recebe estados e ambiente r do ambiente em resposta à ação a . Além disso, às vezes o médium também pode relatar que o episódio terminou. Nesse problema, s é um par de números, o primeiro deles é a posição do carro na curva (uma coordenada é suficiente, já que não podemos nos afastar da superfície) e o segundo é a velocidade na superfície (com um sinal). A recompensa r é um número sempre igual a -1 para esta tarefa. Dessa forma, incentivamos o agente a concluir o episódio o mais rápido possível. Existem apenas três ações possíveis: empurre o carro para a esquerda, não faça nada e empurre o carro para a direita. Essas ações correspondem a números de 0 a 2. O episódio pode terminar se o carro chegar ao topo da colina à direita ou se o agente der 200 passos.

Pouco de teoria

Em Habré já havia um artigo sobre DQN no qual o autor descreveu bastante bem toda a teoria necessária. No entanto, para facilitar a leitura, repetirei aqui de forma mais formal.

A tarefa de aprendizado por reforço é definida por um conjunto de espaço de estado S, espaço de ação A, coeficiente $$$\ gama$, as funções de transição T e as funções de recompensa R. Em geral, a função de transição e a função de recompensa podem ser variáveis ​​aleatórias, mas agora consideraremos uma versão mais simples na qual elas são definidas de forma exclusiva. O objetivo é maximizar as recompensas cumulativas. $$$\ sum_ {t = 0} ^ {T} r_ {t} \ cdot \ gama ^ {t}$, em que t é o número da etapa no meio e T é o número de etapas no episódio.

Para resolver esse problema, definimos a função de valor V do estado s como o valor da recompensa cumulativa máxima, desde que comecemos no estado s. Conhecendo essa função, podemos resolver o problema simplesmente passando a cada passo es com o valor máximo possível. No entanto, nem tudo é tão simples: na maioria dos casos, não sabemos que ação nos levará ao estado desejado. Portanto, adicionamos a ação a como o segundo parâmetro da função. A função resultante é chamada função Q. Ele mostra qual recompensa cumulativa máxima possível podemos obter executando a ação a no estado s. Mas já podemos usar essa função para resolver o problema: estando no estado s, simplesmente escolhemos um tal que Q (s, a) seja máximo.

Na prática, não conhecemos a função Q real, mas podemos aproximá-la por vários métodos. Uma dessas técnicas é a Deep Q Network (DQN). Sua idéia é que, para cada uma das ações, aproximamos a função Q usando uma rede neural.

O meio ambiente

Agora vamos praticar. Primeiro, precisamos aprender como emular o ambiente MountainCar. A biblioteca da academia, que fornece um grande número de ambientes de aprendizado de reforço padrão, nos ajudará a lidar com essa tarefa. Para criar um ambiente, precisamos chamar o método make no módulo de academia, passando o nome do ambiente desejado como parâmetro:

import gym env = gym.make("MountainCar-v0") 

Documentação detalhada pode ser encontrada aqui , e uma descrição do ambiente pode ser encontrada aqui .
Vamos considerar com mais detalhes o que podemos fazer com o ambiente que criamos:

• env.reset() - finaliza o episódio atual e inicia um novo. Retorna o estado inicial.
• env.step(action) - executa a ação especificada. Retorna um novo estado, uma recompensa, se o episódio terminou e informações adicionais que podem ser usadas para depuração.
• env.seed(seed) - define a semente aleatória. Depende de como os estados iniciais serão gerados durante env.reset ().
• env.render() - exibe o estado atual do ambiente.

Percebemos o DQN

DQN é um algoritmo que usa uma rede neural para avaliar uma função Q. No artigo original, o DeepMind definiu a arquitetura padrão para os jogos da Atari usando redes neurais convolucionais. Ao contrário desses jogos, o Mountain Car não usa a imagem como um estado, portanto, teremos que determinar a arquitetura por conta própria.

Tomemos, por exemplo, uma arquitetura com duas camadas ocultas de 32 neurônios em cada uma. Após cada camada oculta, usaremos o ReLU como uma função de ativação. Dois números que descrevem o estado são alimentados na entrada da rede neural e, na saída, obtemos uma estimativa da função Q.

 import torch.nn as nn model = nn.Sequential( nn.Linear(2, 32), nn.ReLU(), nn.Linear(32, 32), nn.ReLU(), nn.Linear(32, 3) ) target_model = copy.deepcopy(model) #    def init_weights(layer): if type(layer) == nn.Linear: nn.init.xavier_normal(layer.weight) model.apply(init_weights) 

Como treinamos a rede neural na GPU, precisamos carregar nossa rede lá:

 #     CPU,  “cuda”    “cpu” device = torch.device("cuda") model.to(device) target_model.to(device) 

A variável do dispositivo será global, pois também precisaremos carregar os dados.

Também precisamos definir um otimizador que atualize os pesos do modelo usando a descida do gradiente. Sim, existem muitos mais de um.

 optimizer = optim.Adam(model.parameters(), lr=0.00003) 

Agora declaramos uma função que considerará a função de erro, o gradiente ao longo dela e aplicará a descida. Mas antes disso, você precisa baixar os dados do lote para a GPU:

 state, action, reward, next_state, done = batch #       state = torch.tensor(state).to(device).float() next_state = torch.tensor(next_state).to(device).float() reward = torch.tensor(reward).to(device).float() action = torch.tensor(action).to(device) done = torch.tensor(done).to(device) 

Em seguida, precisamos calcular os valores reais da função Q; no entanto, como não os conhecemos, iremos avaliá-los através dos valores para o seguinte estado:

 target_q = torch.zeros(reward.size()[0]).float().to(device) with torch.no_grad(): #     Q-function    target_q = target_model(next_state).max(1)[0].view(-1) target_q[done] = 0 target_q = reward + target_q * gamma 

E a previsão atual:

 q = model(state).gather(1, action.unsqueeze(1)) 

Usando target_q e q, calculamos a função de perda e atualizamos o modelo:

 loss = F.smooth_l1_loss(q, target_q.unsqueeze(1)) #      optimizer.zero_grad() #     loss.backward() #   . ,       for param in model.parameters(): param.grad.data.clamp_(-1, 1) #    optimizer.step() 

Como o modelo considera apenas a função Q e não executa ações, precisamos determinar a função que decidirá quais ações o agente executará. Como algoritmo de tomada de decisão, tomamos $$$\ varepsilon$política grega. A ideia dela é que o agente geralmente execute ações com avidez, escolhendo o máximo da função Q, mas com probabilidade $$$\ varepsilon$ele fará uma ação aleatória. Ações aleatórias são necessárias para que o algoritmo possa examinar as ações que ele não executaria guiadas apenas por uma política gananciosa - esse processo é chamado de exploração.

 def select_action(state, epsilon, model): if random.random() < epsilon: return random.randint(0, 2) return model(torch.tensor(state).to(device).float().unsqueeze(0))[0].max(0)[1].view(1, 1).item() 

Como usamos lotes para treinar a rede neural, precisamos de um buffer no qual armazenaremos a experiência de interagir com o ambiente e de onde escolheremos os lotes:

 class Memory: def __init__(self, capacity): self.capacity = capacity self.memory = [] self.position = 0 def push(self, element): """    """ if len(self.memory) < self.capacity: self.memory.append(None) self.memory[self.position] = element self.position = (self.position + 1) % self.capacity def sample(self, batch_size): """    """ return list(zip(*random.sample(self.memory, batch_size))) def __len__(self): return len(self.memory) 

Decisão ingênua

Primeiro, declare as constantes que usaremos no processo de aprendizado e crie um modelo:

 #  model   target model target_update = 1000 #  ,      batch_size = 128 #   max_steps = 100001 #  exploration max_epsilon = 0.5 min_epsilon = 0.1 #    memory = Memory(5000) model, target_model, optimizer = create_new_model() 

Apesar de ser lógico dividir o processo de interação em episódios, para descrever o processo de aprendizado, é mais conveniente dividi-lo em etapas separadas, pois queremos fazer uma etapa de gradiente descendente após cada etapa do ambiente.

Vamos falar mais detalhadamente sobre como uma etapa do aprendizado se parece aqui. Assumimos que agora estamos dando um passo com o número do passo de max_steps steps e o estado atual do estado. Então, fazendo a ação com $$$\ varepsilon$políticas -greedy ficariam assim:

 epsilon = max_epsilon - (max_epsilon - min_epsilon)* step / max_steps action = select_action(state, epsilon, model) new_state, reward, done, _ = env.step(action) 

Adicione imediatamente a experiência adquirida à memória e inicie um novo episódio se o atual terminar:

 memory.push((state, action, reward, new_state, done)) if done: state = env.reset() done = False else: state = new_state 

E daremos o passo da descida do gradiente (se, é claro, já podemos coletar pelo menos um lote):

 if step > batch_size: fit(memory.sample(batch_size), model, target_model, optimizer) 

Agora resta atualizar o target_model:

 if step % target_update == 0: target_model = copy.deepcopy(model) 

No entanto, também gostaríamos de seguir o processo de aprendizado. Para fazer isso, reproduziremos um episódio adicional após cada atualização do target_model com epsilon = 0, armazenando o prêmio total no buffer rewards_by_target_updates:

 if step % target_update == 0: target_model = copy.deepcopy(model) state = env.reset() total_reward = 0 while not done: action = select_action(state, 0, target_model) state, reward, done, _ = env.step(action) total_reward += reward done = False state = env.reset() rewards_by_target_updates.append(total_reward) 

Execute este código e obtenha algo como este gráfico:

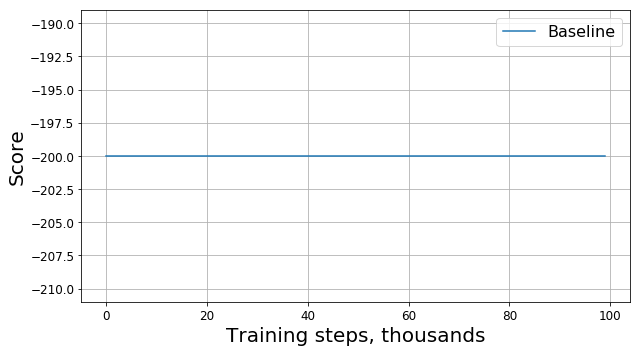
O que deu errado?

Isso é um bug? Esse é o algoritmo errado? Esses parâmetros são ruins? Na verdade não. De fato, o problema está na tarefa, nomeadamente na função da recompensa. Vamos olhar mais de perto. A cada passo, nosso agente recebe uma recompensa de -1, e isso acontece até o final do episódio. Essa recompensa motiva o agente a concluir o episódio o mais rápido possível, mas, ao mesmo tempo, não diz a ele como fazê-lo. Por esse motivo, a única maneira de aprender a resolver um problema em uma formulação desse tipo para um agente é resolvê-lo várias vezes usando a exploração.

Obviamente, alguém poderia tentar usar algoritmos mais complexos para estudar o ambiente em vez do nosso $$$\ varepsilon$políticas de alta qualidade. No entanto, primeiro, devido à sua aplicação, nosso modelo se tornará mais complexo, o que gostaríamos de evitar e, segundo, não o fato de que eles funcionarão bem o suficiente para esta tarefa. Em vez disso, podemos eliminar a fonte do problema modificando a tarefa em si, ou seja, alterando a função de recompensa, ou seja, aplicando o que é chamado de modelagem de recompensa.

Acelerando a convergência

Nosso conhecimento intuitivo nos diz que, para subir a colina, você precisa acelerar. Quanto maior a velocidade, mais próximo o agente de resolver o problema. Você pode contar a ele sobre isso, por exemplo, adicionando um módulo de velocidade com um certo coeficiente à recompensa:

  modified_reward = recompensa + 10 * abs (novo_estado [1]) 

Assim, uma linha na função se ajusta

  memory.push ((estado, ação, recompensa, new_state, done)) 

deve ser substituído por

  memory.push ((estado, ação, recompensa_modificada, novo_estado, concluído)) 

Agora, vejamos o novo gráfico (ele apresenta o prêmio original sem modificações):


Aqui RS é a abreviação de Reward Shaping.

É bom fazer isso?

O progresso é óbvio: nosso agente aprendeu claramente a subir a colina, pois o prêmio começou a diferir de -200. Resta apenas uma pergunta: se alterar a função da recompensa, também alteramos a tarefa, a solução para o novo problema que achamos é boa para o antigo problema?

Para começar, entendemos o que “bondade” significa no nosso caso. Resolvendo o problema, estamos tentando encontrar a política ideal - uma que maximize a recompensa total pelo episódio. Nesse caso, podemos substituir a palavra "bom" pela palavra "ideal", porque estamos procurando por ela. Também esperamos otimista que, mais cedo ou mais tarde, nosso DQN encontre a solução ideal para o problema modificado e não fique preso no máximo local. Portanto, a questão pode ser reformulada da seguinte maneira: se alterar a função da recompensa, também alteramos o problema, a solução ideal para o novo problema que achamos é ideal para o problema antigo?

Como se vê, não podemos fornecer essa garantia no caso geral. A resposta depende de como exatamente mudamos a função da recompensa, como ela foi organizada anteriormente e como o próprio ambiente é organizado. Felizmente, há um artigo cujos autores investigaram como a alteração da função da recompensa afeta a otimização da solução encontrada.

Primeiro, eles encontraram toda uma classe de alterações "seguras", baseadas no método potencial: $$$R '= R + (\ gamma \ cdot \ Phi (novo \ _estado) - \ Phi (estado))$onde $$$\ Phi$- potencial, que depende apenas do estado. Para tais funções, os autores conseguiram provar que se a solução para o novo problema é ótima, então para o antigo problema ela também é ótima.

Em segundo lugar, os autores mostraram que, para qualquer outro $$$R '= R + F (s, a)$existe esse problema, a função de recompensa R e a solução ideal para o problema alterado, que essa solução não é ideal para o problema original. Isso significa que não podemos garantir a qualidade da solução encontrada, se usarmos uma alteração que não seja baseada no método potencial.

Assim, o uso de funções potenciais para modificar a função de recompensa pode alterar apenas a taxa de convergência do algoritmo, mas não afeta a solução final.

Acelere a convergência corretamente

Agora que sabemos como alterar a recompensa com segurança, vamos tentar modificar a tarefa novamente, usando o método potencial em vez de heurísticas ingênuas:

  modified_reward = recompensa + 300 * (gama * abs (novo_estado [1]) - abs (estado [1])) 

Vejamos a programação do prêmio original:



Como se viu, além de ter garantias teóricas, a modificação da recompensa com a ajuda de funções potenciais também melhorou significativamente o resultado, especialmente nos estágios iniciais. Obviamente, há uma chance de que seria possível selecionar hiperparâmetros ótimos (semente aleatória, gama e outros coeficientes) para treinar o agente, mas a forma de recompensa, no entanto, aumenta significativamente a taxa de convergência do modelo.

Posfácio

Obrigado por ler até o fim! Espero que você tenha gostado dessa pequena excursão orientada à prática para o aprendizado reforçado. Está claro que o Mountain Car é uma tarefa de "brinquedo", no entanto, como pudemos observar, ensinar um agente a resolver até uma tarefa aparentemente tão simples do ponto de vista humano pode ser difícil.