Big o

Nota Tradução abreviada, recontando com suas próprias palavras.
UPD: como observado nos comentários, os exemplos não são perfeitos. O autor não está procurando a melhor solução para o problema, seu objetivo é explicar a complexidade dos algoritmos “nos dedos”.

A notação Big O é necessária para descrever a complexidade dos algoritmos. Para isso, é utilizado o conceito de tempo. O tópico é assustador para muitos; os programadores que evitam falar sobre "tempo da ordem N" são comuns.

Se você é capaz de avaliar o código em termos de Big O, provavelmente é considerado um "cara esperto". E provavelmente você passará pela sua próxima entrevista. Você não será questionado se é possível reduzir a complexidade de qualquer parte do código para n log n contra n ^ 2.

Estruturas de dados

A escolha da estrutura de dados depende da tarefa específica: do tipo de dados e do algoritmo para seu processamento. Uma variedade de estruturas de dados (em .NET ou Java ou Elixir) foram criadas para certos tipos de algoritmos.

Frequentemente, escolhendo uma ou outra estrutura, simplesmente copiamos a solução geralmente aceita. Na maioria dos casos, isso é suficiente. Mas, de fato, sem entender a complexidade dos algoritmos, não podemos fazer uma escolha informada. O tópico de estruturas de dados pode ser passado somente após a complexidade dos algoritmos.

Aqui, usaremos apenas matrizes de números (como em uma entrevista). Exemplos de JavaScript.

Vamos começar com o mais simples: O (1)

Tome uma matriz de 5 números:

const nums = [1,2,3,4,5]; 

Suponha que você precise obter o primeiro elemento. Usamos o índice para isso:

 const nums = [1,2,3,4,5]; const firstNumber = nums[0]; 

Quão complicado é esse algoritmo? Podemos dizer: "nada complicado - basta pegar o primeiro elemento da matriz". Isso é verdade, mas é mais correto descrever a complexidade por meio do número de operações executadas para alcançar o resultado, dependendo da entrada ( operações de entrada).

Em outras palavras: quantas operações aumentarão à medida que o número de parâmetros de entrada aumentar.

No nosso exemplo, existem 5 parâmetros de entrada, porque existem 5 elementos na matriz. Para obter o resultado, você precisa executar uma operação (pegue um elemento pelo índice). Quantas operações serão necessárias se houver 100 elementos na matriz? Ou 1000? Ou 100.000? Mesmo assim, apenas uma operação é necessária.

Ou seja: “uma operação para todos os dados de entrada possíveis” - O (1).

O (1) pode ser lido como "complexidade da ordem 1" (ordem 1) ou "o algoritmo é executado em tempo constante / constante" (tempo constante).

Você já adivinhou que os algoritmos O (1) são os mais eficientes.

Iterações e "hora da ordem n": O (n)

Agora vamos encontrar a soma dos elementos da matriz:

 const nums = [1,2,3,4,5]; let sum = 0; for(let num of nums){ sum += num; } 

Novamente nos perguntamos: quantas operações de entrada precisamos? Aqui você precisa classificar todos os elementos, ou seja, operação em cada elemento. Quanto maior a matriz, mais operações.

Usando a notação Big O: O (n) ou "complexidade da ordem n (ordem n)". Além disso, esse tipo de algoritmo é chamado de "linear" ou que o algoritmo é "linearmente dimensionado".

Análise

Podemos tornar a soma mais eficiente? Geralmente não. E se sabemos que a matriz é garantida para iniciar em 1, classificada e sem lacunas? Em seguida, podemos aplicar a fórmula S = n (n + 1) / 2 (em que n é o último elemento da matriz):

 const sumContiguousArray = function(ary){ //get the last item const lastItem = ary[ary.length - 1]; //Gauss's trick return lastItem * (lastItem + 1) / 2; } const nums = [1,2,3,4,5]; const sumOfArray = sumContiguousArray(nums); 

Esse algoritmo é muito mais eficiente que O (n), além disso, é executado em "tempo constante / constante", ou seja, é O (1).

De fato, há mais de uma operação: você precisa obter o comprimento da matriz, obter o último elemento, executar multiplicação e divisão. Não é O (3) ou algo assim? Na notação Big O, o número real de etapas não é importante, é importante que o algoritmo seja executado em tempo constante.

Os algoritmos de tempo constante são sempre O (1). O mesmo com algoritmos lineares, de fato, as operações podem ser O (n + 5), no Big O a notação é O (n).

Não são as melhores soluções: O (n ^ 2)

Vamos escrever uma função que verifique se há duplicatas na matriz. Solução de loop aninhado:

 const hasDuplicates = function (num) { //loop the list, our O(n) op for (let i = 0; i < nums.length; i++) { const thisNum = nums[i]; //loop the list again, the O(n^2) op for (let j = 0; j < nums.length; j++) { //make sure we're not checking same number if (j !== i) { const otherNum = nums[j]; //if there's an equal value, return if (otherNum === thisNum) return true; } } } //if we're here, no dups return false; } const nums = [1, 2, 3, 4, 5, 5]; hasDuplicates(nums);//true 

Já sabemos que a iteração da matriz é O (n). Temos um loop aninhado, para cada elemento iteramos novamente - ou seja, O (n ^ 2) ou "complexidade da ordem n quadrada".

Algoritmos com loops aninhados sobre a mesma coleção são sempre O (n ^ 2).

"A complexidade da ordem do log n": O (log n)

No exemplo acima, um loop aninhado, por si só (se você não considerar que está aninhado), tem complexidade O (n), porque é enumeração de elementos da matriz. Esse ciclo termina assim que o elemento desejado é encontrado, ou seja, de fato, nem todos os elementos serão enumerados. Mas a notação Big O sempre considera o pior cenário possível - o item que você está procurando pode ser o último.

Aqui, um loop aninhado é usado para procurar um determinado elemento em uma matriz. A busca de um elemento em uma matriz, sob certas condições, pode ser otimizada - feita melhor que O (n) linear.

Deixe a matriz ser classificada. Então, podemos usar o algoritmo de busca binária: divida a matriz em duas metades, descarte o desnecessário, divida o restante novamente em duas partes e assim por diante até encontrarmos o valor desejado. Esse tipo de algoritmo é chamado de dividir e conquistar Dividir e conquistar.



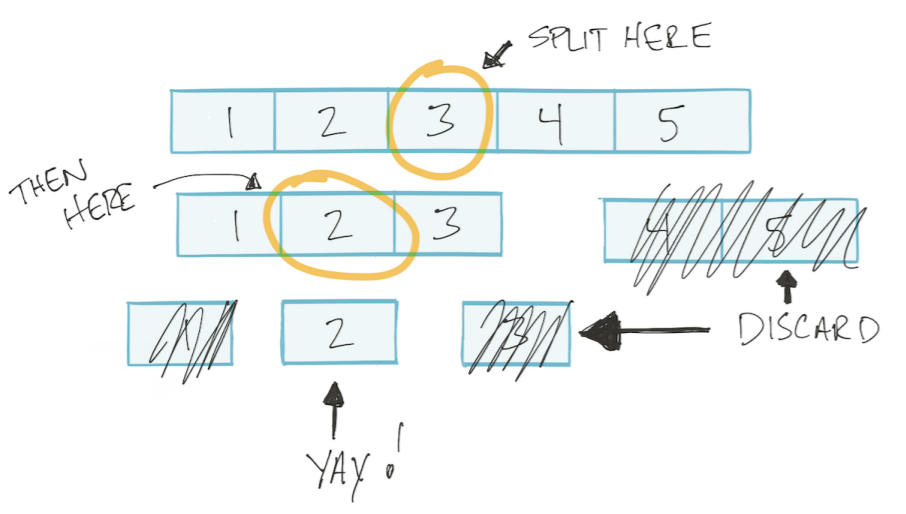
Este algoritmo é baseado em um logaritmo.

Visão geral rápida dos logaritmos

Considere um exemplo, qual será x?

x ^ 3 = 8

Precisamos pegar a raiz cúbica de 8 - isso será 2. Agora, mais difícil

2 ^ x = 512

Usando o logaritmo, o problema pode ser escrito como

log2 (512) = x

"O logaritmo base 2 de 512 é x." Preste atenção à "base 2", ou seja, pensamos em dois - quantas vezes você precisa multiplicar 2 para obter 512.

No algoritmo de busca binária, em cada etapa, dividimos o array em duas partes.

Minha adição. I.e. na pior das hipóteses, realizamos tantas operações quanto podemos dividir a matriz em duas partes. Por exemplo, quantas vezes podemos dividir uma matriz de 4 elementos em duas partes? 2 vezes. E uma matriz de 8 elementos? 3 vezes. I.e. número de divisões / operações = log2 (n) (onde n é o número de elementos na matriz).

Acontece que a dependência do número de operações com o número de elementos de entrada é descrita como log2 (n)


Assim, usando a notação Big O, o algoritmo de busca binária tem complexidade O (log n).

Melhorar O (n ^ 2) para O (n log n)

Vamos voltar à tarefa de verificar se há duplicatas na matriz. Nós iteramos sobre todos os elementos da matriz e, para cada elemento, iteramos novamente. Eles fizeram O (n) dentro de O (n), ou seja, O (n * n) ou O (n ^ 2).

Podemos substituir o loop aninhado por uma pesquisa binária *. I.e. nós apenas temos que passar por todos os elementos de O (n), dentro de nós fazemos O (log n). Acontece O (n * log n) ou O (n log n).

 const nums = [1, 2, 3, 4, 5]; const searchFor = function (items, num) { //use binary search! //if found, return the number. Otherwise... //return null. We'll do this in a later chapter. } const hasDuplicates = function (nums) { for (let num of nums) { //let's go through the list again and have a look //at all the other numbers so we can compare if (searchFor(nums, num)) { return true; } } //only arrive here if there are no dups return false; } 

* ATENÇÃO, a fim de evitar impressões . Usar a pesquisa binária para verificar se há duplicatas em uma matriz é uma solução ruim. Ele mostra apenas como, em termos de Big O, avaliar a complexidade do algoritmo mostrado na lista de códigos acima. Um bom ou ruim algoritmo não é importante para este artigo; a visibilidade é importante.

Pensando em termos de Big O

• A obtenção do item de coleção é O (1). Seja obtendo por índice em uma matriz ou por chave em um dicionário na notação Big O, será O (1)
• A iteração sobre uma coleção é O (n)
• Os loops aninhados sobre a mesma coleção são O (n ^ 2)
• Dividir e conquistar sempre O (log n)
• As iterações que usam Divide e Conquer são O (n log n)