Lembro-me de uma conclusão importante das partes anteriores. Para um comportamento seqüencial cíclico que não contém vários sinais (alternando um ciclo mais de duas vezes), a função lógica mínima de cada sinal pode ser representada da seguinte forma (naturalmente, na ausência de conflitos de CSC):
1)
onde a * b * ... * c é o implicante de uma ou mais variáveis. g + h + ... + i - este é possivelmente um conjunto vazio de implicantes que consiste em uma variável. x * f é um implante de 2 variáveis, cuja presença em uma forma mínima não é necessária. Todas as variáveis, exceto x, podem ser incluídas na fórmula tanto na forma direta quanto na inversa, dependendo da disposição dos sinais dos eventos correspondentes. Todas as variáveis são incluídas na fórmula como argumentos estritamente uma vez.
Antes de prosseguir, examinaremos mais de perto um fenômeno como a decomposição. Antes de tudo, a decomposição é interessante, o que preserva a auto-sincronização. Ao decompor uma função lógica NOT-AND-OR, é possível distinguir como um novo elemento:
a) um ou mais implicantes,
b) vários sinais (variáveis) de um implante,
c) um inversor de entrada.
Para começar, consideramos um caso especial da função NOR AND. O comportamento de uma função lógica (x = a + b + c + d) para o modelo em questão:
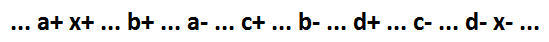
Ela pode distinguir vários sinais como um elemento separado.
De fato, a seleção de um novo elemento durante a decomposição é a adição de um novo sinal (f). Para manter o comportamento correto, a semi-modularidade e a sincronização automática, a comutação do sinal recém-adicionado f deve ter eventos de conseqüência. Como a decomposição afeta apenas um elemento do circuito (neste caso, x) e não afeta os elementos restantes do circuito, a troca do sinal f só pode causar a troca do sinal x. Caso contrário, a função lógica de outro sinal dependeria do sinal f. Dada essa conclusão, vamos tentar destacar várias variáveis, exceto a variável a como um novo elemento f. Tomemos, por exemplo, as variáveis bec. Eles formam o elemento lógico f = b + c.
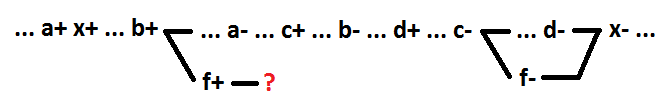
Como pode ser visto, para o evento f + é impossível determinar o evento de conseqüência sem violar a correção do comportamento. Qualquer grupo de sinais que não contenha a variável a não pode ser alocado como um elemento separado enquanto mantém a auto-sincronização.
Um sinal como um neste exemplo será chamado de ativação. No caso geral, o sinal de comutação para a função OR (AND) é um sinal, alternando para 1 (0) altera o valor da função de 0 para 1 (de 1 para 0). Para manter a auto-sincronização durante a decomposição da função lógica OR (AND) ao selecionar um novo elemento, você deve usar o sinal de comutação. Ao selecionar um novo elemento, também é necessário usar apenas os sinais que formam uma cadeia conectada (no exemplo abaixo a + b). x = f + c + d, f = a + b.
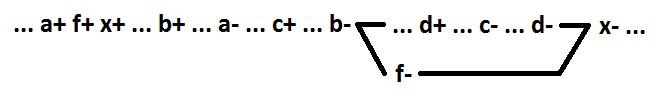
Ao usar sinais a + b + d, a auto-sincronização não é preservada.
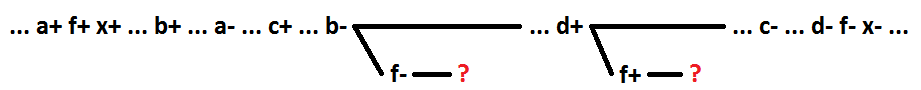
Assim, para comportamentos sequenciais sem múltiplos sinais durante a decomposição da função lógica OR (I), destacando como o novo elemento os primeiros no decurso da implantação do processo de sinal, a partir do processo de comutação, garante a auto-sincronização do circuito.
Agora considere a função não OR (x =! A +! B). Como um elemento separado (f), mantendo o auto-sincronismo, podemos selecionar apenas o inversor de entrada que corresponde ao sinal de comutação (x = f +! B, f =! A). A separação de outros inversores de entrada como elemento separado levará a uma violação da auto-sincronização.
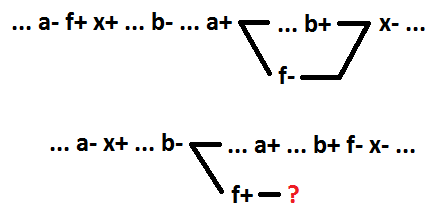
Vamos para a função AND-OR. Da mesma forma, como sinal de comutação para a função OR, definimos a comutação implicante para a função AND-OR. Isso é um implicante, alterar o valor de 0 para 1 leva a uma alteração no valor da função de 0 para 1. Da mesma forma, como foi descoberto para a função OR, para comportamentos sequenciais sem múltiplos sinais ao decompor a função lógica AND-OR, selecionando os primeiros como um novo elemento no processo de implantação, o implicante, a partir da inclusão, garante a preservação da auto-sincronização do circuito. Caso contrário, a auto-sincronização será interrompida. No exemplo abaixo, antes da decomposição x = a * b + c. Após a decomposição, x = f + c, f = a * b.
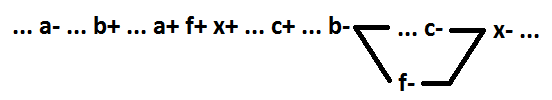
Agora, para a função AND-OR, consideramos a seleção como um novo elemento de várias variáveis incluídas no mesmo implicante. Somente funções mínimas são consideradas. Abaixo estão todas as opções possíveis para o exemplo da função x = a * b * c + d (para a opção 4 - x = a * b * c + d + e, para a opção 6 - x = a * b * c * d + e) . O elemento destacado é f = a * b.

Na opção 1, alternar um dos sinais alocados (a +) é a causa do evento x +. Na opção 2, a comutação de um dos sinais alocados (a) é a causa do evento x. Nas opções 3 e 4, a comutação de um dos sinais alocados (a + e a-, respectivamente) está localizada entre os eventos x + e x-, e não é a causa do evento x-. A opção 5 é um caso especial da opção 4, quando o implicante, no qual os sinais são alocados, é inclusivo. A opção restante 6 - todas as comutações dos sinais alocados estão localizadas entre os eventos x- e x +, e não são as causas do evento x +.
Como você pode ver, nas opções 1 e 6, o evento f não pode ser posicionado corretamente. Tais transformações não são decompostas com preservação da auto-sincronização. Nas opções 2, 3 e 4, a auto-sincronização é mantida. Mas o valor da função x acaba sendo diferente de f * c + d (f * c + d + e para 4 opções). Para 2 opções - x = f * (d + c), para 3 opções x = c * x + d *! F + x *! F, para 4 opções x = (f + d) * (e + c). Tais transformações não são decomposições.
Somente a opção 5 é uma decomposição com preservação da auto-sincronização (x = f * c + d). Nesse caso, como um elemento separado no implicante de inclusão, os primeiros vários sinais são selecionados, começando com a inclusão (o sinal incluindo o implicante de E é o mesmo que o sinal incluindo a função de AND). Mas, como mostrado acima, um resultado semelhante é alcançado em duas etapas. Primeiro, a inclusão do implante é destacada. Na segunda etapa, os primeiros sinais são selecionados no novo elemento, começando com o sinal de comutação.
Vamos para a função NÃO-E-OU. Vamos destacar o inversor de entrada como um elemento separado. O sinal a corresponde à entrada do elemento x, à qual um inversor de entrada dedicado está conectado (f =! A).
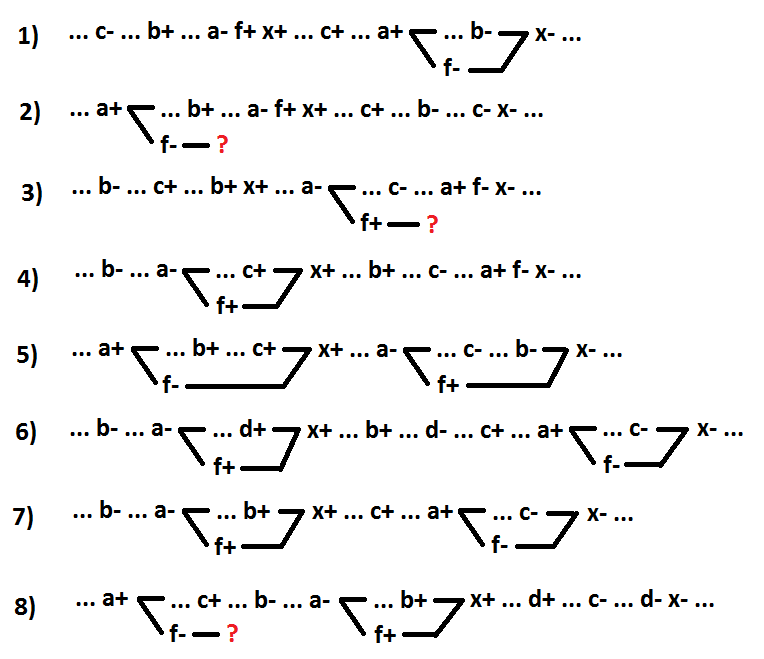
Opções 1 e 2 - sinal de comutação a é a causa do evento x + (1 - x =! A + b * c, 2 - x = b *! A + c). Opções 3 e 4 - alternar o sinal a é a causa do evento x- (3 - x =! A + b * c, 4 - x =! A * b + c). As opções 5 e 6 - a comutação do sinal a está localizada entre os eventos x + e x-, e não é a causa do evento x- (5 - x = b *! A + c, 6 - x =! A * b + d + c). A opção 7 é um caso especial da opção 6, quando o sinal a é um sinal de comutação incluindo implicantes (x =! A * b + c). A opção 8 restante - todos os comutadores de sinal a estão localizados entre os eventos x- e x +, e não são as causas do evento x + (x = c *! A * b + d).
Como você pode ver, as opções 2, 3 e 8 não são uma decomposição com preservação da auto-sincronização, pois é impossível posicionar corretamente a comutação do sinal f. Para a opção 4, após a conversão x = f * (c + b). Para a opção 5, após a conversão x = c *! F +! F * x + b * x. Para a opção 6, após a conversão x = (f + c) * (d + b). Essas transformações (opções 4, 5 e 6) não são decomposições. Para a opção 7, após a conversão x = f * b + c. A opção 7 é uma decomposição com preservação da auto-sincronização. Neste caso, um inversor correspondente ao sinal de comutação incluindo os implantes é alocado como um elemento separado. Um resultado semelhante é alcançado em duas etapas usando as transformações acima. Primeiro, a inclusão do implicante é destacada e, em seguida, o inversor de entrada do sinal de ativação é alocado a ele. Para a opção 1, após a conversão x = f + b * c. A opção 1 também é uma decomposição com preservação da auto-sincronização. Este é um caso especial da opção 7, quando a inclusão do implicante consiste em um sinal.
Sistematizamos os resultados obtidos. Para o modelo em consideração, ao decompor uma função lógica NOT-AND-OR para manter o auto-sincronismo, apenas as seguintes transformações são possíveis - alocação como um elemento separado:
1 - um ou mais, a partir do implicante inclusivo sobreposto (um caso especial - para a função de NÃO selecionar OU de vários sinais sobrepostos, começando pelo inclusivo);
2 - na inclusão implicante de vários, a partir da inclusão, sobreposição de sinais;
3 - inversor de entrada correspondente ao sinal de comutação, incluindo implicantes (um caso especial - para a função de seleção NÃO OU do inversor de entrada correspondente ao sinal de comutação).
Essas transformações não permitem que o implicante seja inclusivo se não fosse antes da transformação. Daí a conclusão: se uma função lógica contiver um implicante, que consiste em mais de um sinal e não é inclusivo, essa função não pode ser fragmentada usando uma decomposição que preserva a auto-sincronização, com até dois elementos de entrada. Qualquer função lógica NOT-AND-OR na qual mais de uma variável contenha apenas um implicante inclusivo pode ser dividida em até dois elementos de entrada (2AND-NOT, 2OR-NOT) usando uma decomposição que preserva a auto-sincronização.
Etapa 1 - se o elemento lógico contiver apenas um implicante (ou todos os implicantes consistem em uma variável), vá para a etapa 3, caso contrário, vá para a etapa 2.
Etapa 2 - selecione como um elemento separado todos os implantes, exceto um, começando com a inclusão. Em seguida, trabalhamos com o item recém-recebido. Vá para o passo 1.
Etapa 3 - se o elemento consistir em duas variáveis, vá para a etapa 5, caso contrário, vá para a etapa 4.
Etapa 4 - selecionamos como elemento separado todas as variáveis, exceto uma, começando com a inclusão. Em seguida, trabalhamos com o item recém-recebido. Vá para o passo 3.
Etapa 5 - aplica-se a todos os elementos de duas entradas recebidos.
Etapa 5.1 - se os inversores de entrada estiverem nas duas entradas, converteremos o elemento em dual.
Etapa 5.2 - se o inversor de entrada for um e corresponder a um sinal que não está sendo ligado, converteremos o elemento em um duplo.
Etapa 5.3 - o inversor de entrada, se houver, é destacado como um elemento separado. Esmagamento concluído.
Agora, volte à fórmula 1 no início do texto. Se o implicante x * f não estiver na expressão lógica, a função será assim: x = a * b * c + g + h + i. O comportamento dela:
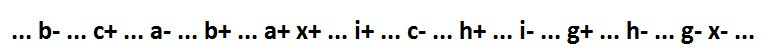
Como você pode ver, o único implicante de mais de uma variável (a * b * c) é inclusivo. E essa função com a ajuda da decomposição pode ser fragmentada para os componentes mínimos, mantendo a auto-sincronização.
Se o implicante x * f estiver presente em uma expressão lógica, a função será assim: x = a * b * c + x * f + g + h + i. O comportamento dela:
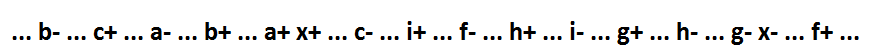
O implicante x * f não inclusivo consiste em mais de uma variável. Essa função não pode ser fragmentada enquanto mantém a auto-sincronização. Mas aplicamos uma transformação que preserva a auto-sincronização: adicione o sinal y - dual ao sinal x. A adição do sinal y altera a função apenas do sinal x e do sinal cuja comutação foi uma conseqüência do evento x- (a variável x é substituída pela variável y).
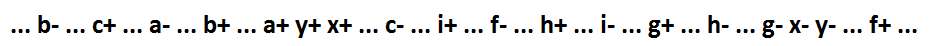
Agora x = (f + i + h + g) * y, y = c * b * a + x. Os implicantes f + i + h + ge ec * b * a incluindo e, respectivamente, as funções x e y podem ser fragmentados para os componentes mínimos, mantendo a auto-sincronização.
Um modelo simplificado de comportamento (sem paralelismo, escolha e múltiplos sinais) permite identificar propriedades que são naturalmente inerentes aos processos binários. A síntese de circuitos auto-síncronos em uma base mínima é um fenômeno natural que não requer nenhum projeto.