Em um artigo anterior, apontei quão difundido é o problema do uso indevido do critério t em publicações científicas (e isso só pode ser feito graças à sua abertura e que lixo é criado quando usado em qualquer curso, relatório, tarefa de treinamento etc. - é desconhecido) . Para discutir isso, falei sobre os fundamentos da análise de variância e o nível de significância α estabelecido pelo próprio pesquisador. Mas, para uma compreensão completa de todo o quadro da análise estatística, é necessário enfatizar uma série de coisas importantes. E o mais básico deles é o conceito de erro.
Erro e aplicação incorreta: qual é a diferença?
Qualquer sistema físico contém algum tipo de erro, imprecisão. Na forma mais diversa: a chamada tolerância - a diferença de tamanho de diferentes produtos do mesmo tipo; característica não linear - quando um dispositivo ou método mede algo de acordo com uma lei conhecida dentro de certos limites e depois se torna inaplicável; discrição - quando somos tecnicamente incapazes de garantir uma característica de saída suave.
E, ao mesmo tempo, há um erro puramente humano - uso incorreto de dispositivos, instrumentos, leis matemáticas. Há uma diferença fundamental entre o erro inerente ao sistema e o erro na aplicação desse sistema. É importante distinguir e não confundir entre si esses dois conceitos, chamados a mesma palavra "erro". Neste artigo, prefiro usar a palavra "erro" para indicar as propriedades do sistema e "uso incorreto" - por seu uso incorreto.
Ou seja, o erro da régua é igual à tolerância do equipamento, colocando traços em sua tela. Um erro no sentido de uso incorreto seria usá-lo ao medir os detalhes de um relógio. O erro da balança está escrito nele e equivale a cerca de 50 gramas, e o uso indevido da balança seria pesar uma sacola de 25 kg, que se estende da mola da região da lei de Hooke à região de deformações plásticas. O erro de um microscópio de força atômica deriva de sua discrição - você não pode "tocar" objetos com uma sonda menor do que com o diâmetro de um átomo. Mas há muitas maneiras de usá-lo ou interpretar mal os dados. E assim por diante
Então, que tipo de erro isso tem nos métodos estatísticos? E esse erro é precisamente o notório nível de significância α.
Erros do primeiro e do segundo tipo
Um erro no aparato matemático da estatística é sua própria essência probabilística bayesiana. No último artigo, eu já mencionei em que métodos estatísticos são baseados: determinar o nível de significância α como a maior probabilidade aceitável de rejeitar ilegalmente a hipótese nula, e o pesquisador atribuir esse valor de forma independente ao pesquisador.
Você já viu esta convenção? De fato, nos métodos de critérios não há rigor matemático familiar. A matemática opera com características probabilísticas.
E aqui chega outro ponto em que é possível uma má interpretação de uma palavra em um contexto diferente. É necessário distinguir entre o conceito de probabilidade e a implementação real de um evento, expressa na distribuição de probabilidade. Por exemplo, antes de iniciar qualquer um de nossos experimentos, não sabemos que tipo de valor obteremos como resultado. Existem dois resultados possíveis: tendo obtido um certo valor do resultado, nós o obteremos ou não. É lógico que a probabilidade de ambos os eventos seja 1/2. Mas a curva gaussiana mostrada no artigo anterior mostra
a distribuição de probabilidade que supomos corretamente a coincidência.
Você pode ilustrar isso claramente com um exemplo. Vamos jogar dois dados 600 vezes - regular e trapacear. Obtemos os seguintes resultados:

Antes do experimento, para ambos os cubos, a perda de qualquer face será igualmente provável - 1/6. No entanto, após o experimento, a essência do cubo de trapaça aparece, e podemos dizer que a densidade de probabilidade dos seis que caem sobre ele é de 90%.
Outro exemplo que os químicos, físicos e qualquer pessoa interessada em efeitos quânticos conhece são os orbitais atômicos. Teoricamente, um elétron pode ser "manchado" no espaço e localizado em quase qualquer lugar. Mas, na prática, há áreas em 90% ou mais dos casos. Essas regiões do espaço formadas por uma superfície com uma densidade de probabilidade de um elétron de 90% são orbitais atômicos clássicos na forma de esferas, halteres, etc.
Portanto, ao definir independentemente o nível de significância, concordamos deliberadamente com o erro descrito em seu nome. Por esse motivo, nem um único resultado pode ser considerado "completamente confiável" - sempre nossas conclusões estatísticas conterão alguma probabilidade de falha.
Um erro formulado determinando o nível de significância α é chamado de
erro do primeiro tipo . Pode ser definido como um "falso alarme" ou, mais corretamente, um resultado falso positivo. De fato, o que as palavras “rejeitam erroneamente a hipótese nula” significam? Isso significa tomar erroneamente os dados observados para diferenças significativas entre os dois grupos. Para fazer um diagnóstico falso sobre a presença da doença, apressar-se a revelar ao mundo uma nova descoberta, que na verdade não existe - esses são exemplos de erros de primeiro tipo.
Mas então, deve haver resultados negativos falsos? Muito bem, e eles são chamados de
erros do segundo tipo . Os exemplos são um diagnóstico prematuro ou decepção como resultado de um estudo, embora na verdade contenha dados importantes. Erros do segundo tipo são indicados pela letra, curiosamente, β. Mas esse conceito em si não é tão importante para as estatísticas quanto o número 1-β. O número 1-β é chamado de
força do critério e, como você pode imaginar, caracteriza a capacidade do critério de não perder um evento significativo.
No entanto, o conteúdo nos métodos estatísticos de erros de primeiro e segundo tipos não é apenas sua limitação. O próprio conceito desses erros pode ser usado diretamente na análise estatística. Como
Análise ROC
A análise ROC (da característica de operação do receptor) é um método para quantificar a aplicabilidade de um determinado atributo a uma classificação binária de objetos. Simplificando, podemos criar uma maneira de distinguir pessoas doentes de pessoas saudáveis, gatos de cães, preto de branco e verificar a validade desse método. Vejamos um exemplo novamente.
Seja você um cientista forense iniciante e desenvolva uma nova maneira de determinar de maneira discreta e inequívoca se uma pessoa é um criminoso. Você veio com um sinal quantitativo: avaliar as inclinações criminais das pessoas pela frequência em que ouvem Mikhail Krug. Mas seu sintoma dará resultados adequados? Vamos acertar.
Você precisará de dois grupos de pessoas para validar seus critérios: cidadãos comuns e criminosos. De fato, vamos supor que o tempo médio anual que eles ouvem Mikhail Krug seja diferente (veja a figura):
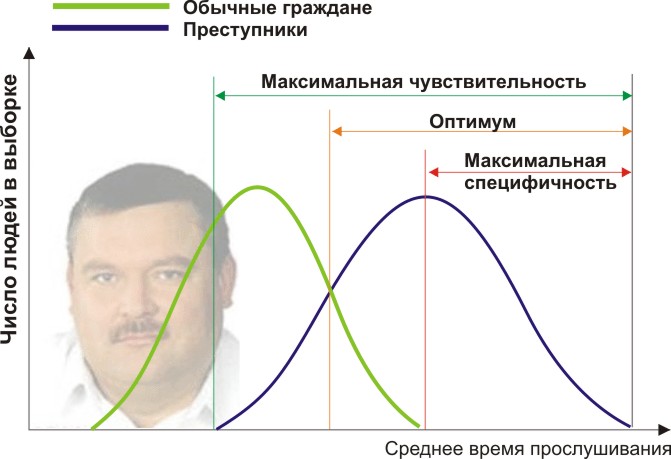
Aqui vemos que, pelo sinal quantitativo do tempo de audição, nossas amostras se cruzam. Alguém ouve o Círculo espontaneamente no rádio sem cometer crimes, e alguém infringe a lei ouvindo outras músicas ou mesmo sendo surdo. Que condições de contorno nós temos? A análise ROC apresenta os conceitos de seletividade (sensibilidade) e especificidade. Sensibilidade é definida como a capacidade de identificar todos os pontos de interesse para nós (neste exemplo, criminosos) e a especificidade - para não capturar nada de falso positivo (para não suspeitar de habitantes comuns). Podemos definir algumas características quantitativas críticas que separam algumas das outras (laranja), variando entre a sensibilidade máxima (verde) e a máxima especificidade (vermelho).
Vejamos o seguinte diagrama:

Ao mudar o valor do nosso atributo, alteramos a proporção de resultados falso-positivos e falso-negativos (a área sob as curvas). Da mesma forma, podemos definir Sensibilidade = Posição. Res-t / (Res-positivo + falso-negativo. Res-t) e Especificidade = Neg. Res-t / (Res negativo-t + falso positivo. Res-t).
Porém, o mais importante é que podemos avaliar a proporção de resultados positivos para falsos positivos em toda a faixa de valores de nosso atributo quantitativo, que é a nossa curva ROC desejada (veja a figura):

E como entendemos neste gráfico quão bom é nosso atributo? Muito simples, calcule a área sob a curva (AUC, área sob a curva). A linha tracejada (0,0; 1,1) significa a completa coincidência das duas amostras e um critério completamente sem sentido (a área sob a curva é de 0,5 do quadrado inteiro). Mas a convexidade da curva ROC apenas indica a perfeição do critério. Se conseguirmos encontrar um critério que as amostras não se cruzem, a área sob a curva ocupará todo o gráfico. Em geral, a característica é considerada boa, permitindo separar uma amostra de outra com confiabilidade se AUC> 0,75-0,8.
Com esta análise, você pode resolver uma variedade de problemas. Tendo decidido que muitas donas de casa estavam sob suspeita por causa de Michael Krug e, além disso, reincidentes perigosos ouvindo Noggano foram perdidos, você pode rejeitar esse critério e desenvolver outro.
Tendo emergido como uma maneira de processar sinais de rádio e identificar "amigo ou inimigo" após um ataque a Pearl Harbor (daí o nome estranho para as características dos receptores), a análise ROC encontrou ampla aplicação em estatísticas biomédicas para análise, validação, criação e caracterização de painéis de biomarcadores etc. É flexível de usar se for baseada na lógica do som. Por exemplo, você pode desenvolver indicações para o exame médico de pacientes centrais aposentados aplicando um critério altamente específico, aumentando a eficiência da detecção de doenças cardíacas e não sobrecarregando os médicos com pacientes desnecessários. E durante uma perigosa epidemia de um vírus anteriormente desconhecido, pelo contrário, você pode criar um critério altamente seletivo para que ninguém mais escape literalmente da vacinação.
Encontramos erros de ambos os tipos e sua visibilidade na descrição dos critérios validados. Agora, partindo dessas bases lógicas, podemos destruir uma série de falsas descrições estereotipadas dos resultados. Algumas formulações incorretas capturam nossas mentes, muitas vezes confundidas com suas palavras e conceitos semelhantes, e também devido à pouca atenção dada à interpretação incorreta. Talvez isso precise ser escrito separadamente.