Algoritmo de triangulação de Delaunay pelo método da linha de varredura

Bom dia

Neste artigo, descreverei em detalhes o algoritmo que obtive como resultado da idéia de "varrer a linha reta" para construir a triangulação de Delaunay em um plano. Existem várias idéias que nunca encontrei quando li artigos sobre triangulação.
Talvez alguém também os ache incomuns. Tentarei fazer tudo da melhor tradição e incluir o seguinte na história: uma descrição das estruturas de dados usadas, uma descrição das etapas do algoritmo, prova de correção, estimativas de tempo e uma comparação com um algoritmo iterativo usando a árvore kD.

Definições e declaração do problema

Triangulação

Diz-se que a triangulação é dada no conjunto de pontos no plano se alguns pares de pontos são conectados por uma aresta, qualquer face finita no gráfico resultante forma um triângulo, as arestas não se cruzam e o gráfico é máximo no número de arestas.

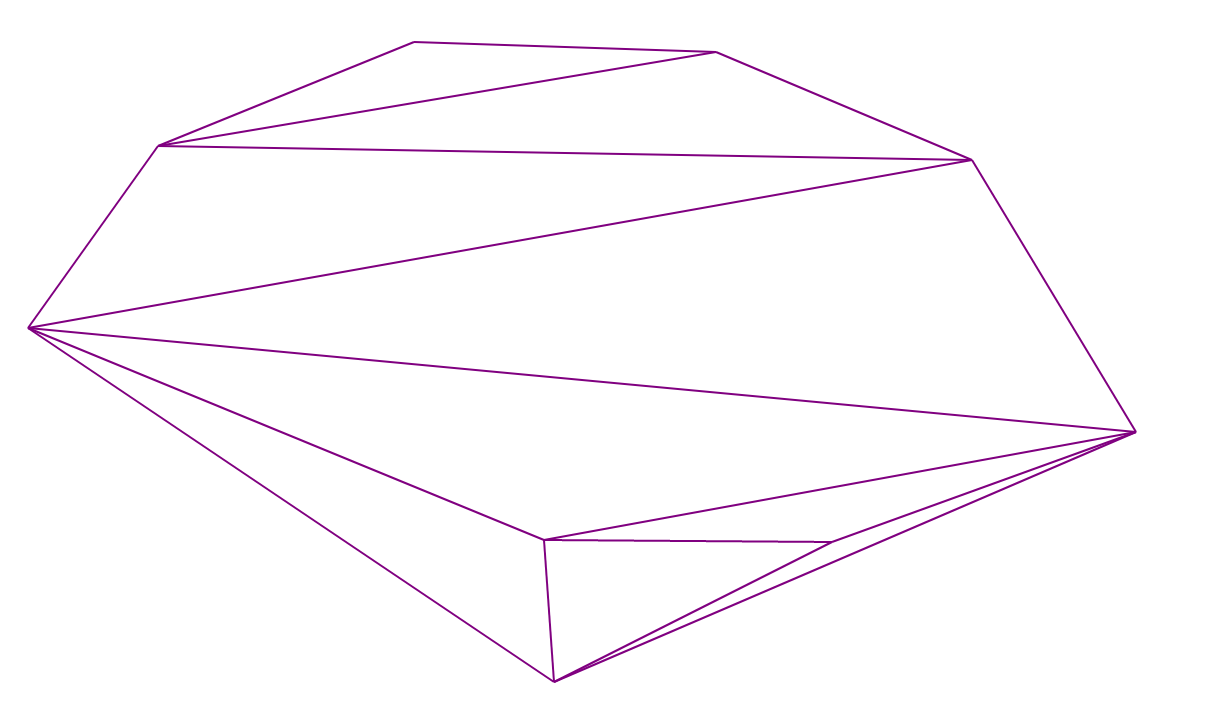
Triangulação de Delaunay

Uma triangulação de Delaunay é uma triangulação na qual, para qualquer triângulo, é verdade que não há pontos do conjunto original dentro do círculo circunscrito ao seu redor.

Nota : para um determinado conjunto de pontos em que não há 4 pontos no mesmo círculo, existe exatamente uma triangulação em Delaunay.

A Condição de Delaunay

Seja dada uma triangulação no conjunto de pontos. Dizemos que um determinado subconjunto de pontos satisfaz a condição de Delaunay se a triangulação delimitada nesse subconjunto for a triangulação de Delaunay para ele.

Critério para triangulação de Delaunay

O cumprimento da condição de Delaunay para todos os pontos que formam um quadrângulo em uma triangulação é equivalente ao fato de que essa triangulação é uma triangulação de Delaunay.

Nota : para quadrângulos não convexos, a condição de Delaunay é sempre preenchida e para quadrângulos convexos (cujos vértices não estão no mesmo círculo), existem exatamente 2 triangulações possíveis (uma das quais é a triangulação de Delaunay).

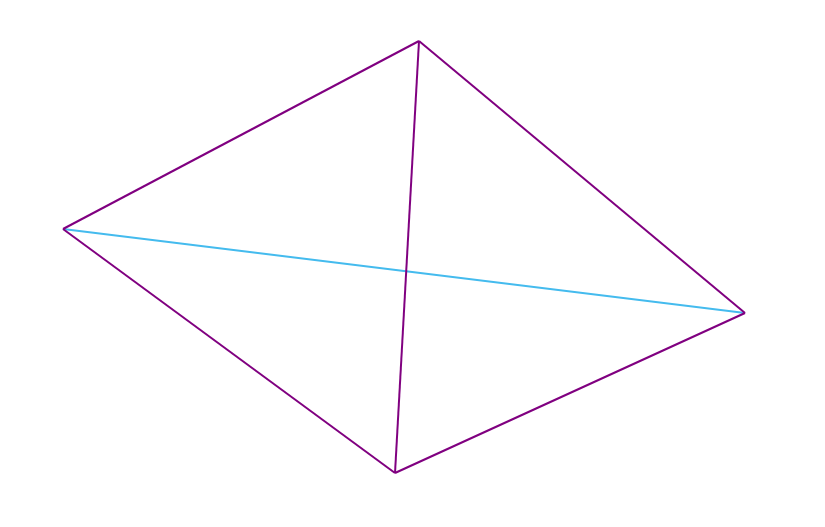
A tarefa é construir uma triangulação de Delaunay para um determinado conjunto de pontos.

Descrição do algoritmo

Pontos visíveis e arestas visíveis

Seja dado um casco mínimo convexo (doravante, MBO) de um conjunto finito de pontos (arestas conectando alguns dos pontos para formar um polígono contendo todos os pontos do conjunto) e um ponto A localizado fora do casco. Em seguida, o ponto do plano é chamado visível para o ponto A, se o segmento que o conectar ao ponto A não cruzar o MBO.

Uma borda do MBO é chamada visível para o ponto A se suas extremidades são visíveis para A.

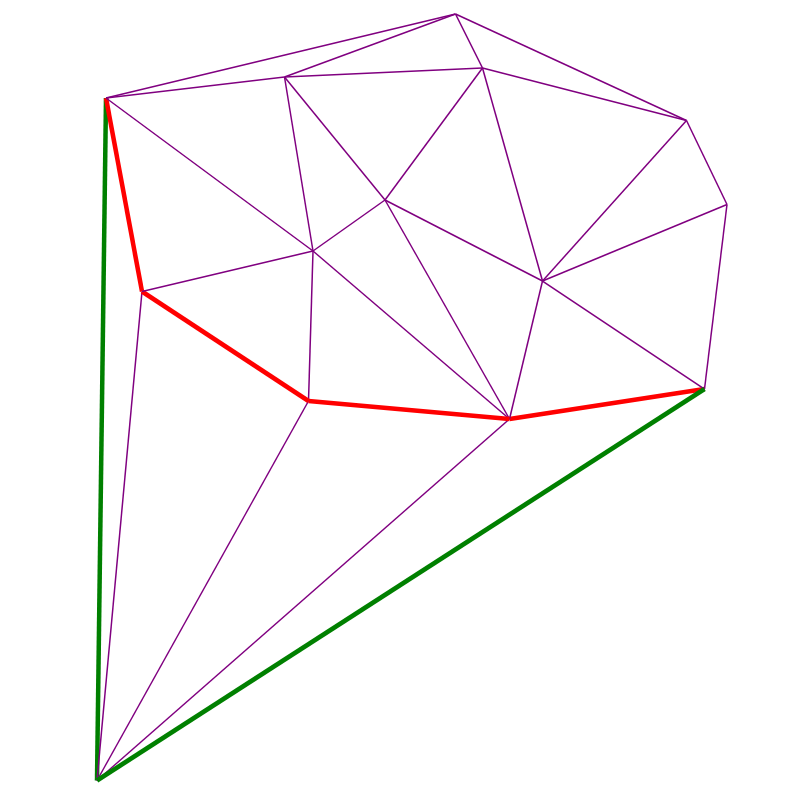
Na imagem a seguir, as bordas visíveis para o ponto vermelho estão marcadas em vermelho:

Nota : o contorno da triangulação de Delaunay é o MBO para os pontos nos quais é construído.

Observação 2 : no algoritmo, as arestas visíveis para o ponto adicionado A formam uma cadeia, ou seja, várias arestas de MBO seguidas

Armazenando triangulação na memória

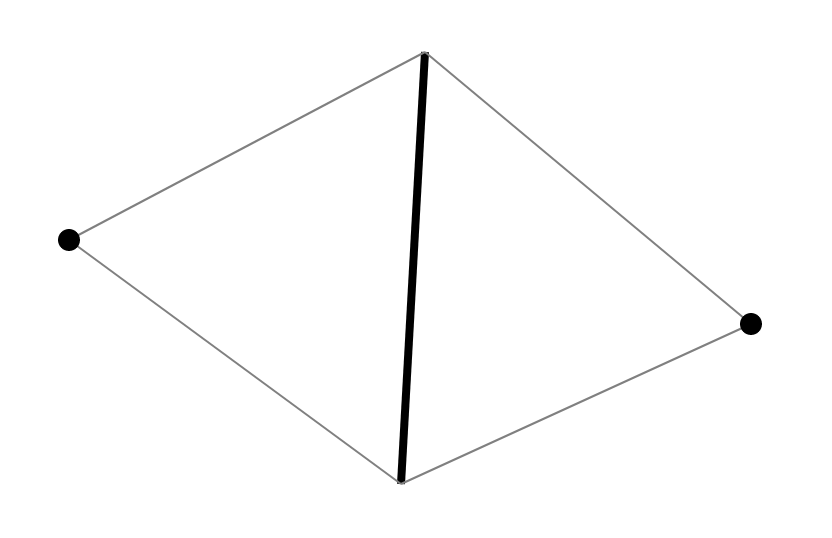
Existem alguns métodos padrão que são bem descritos no livro de Skvortsov [1]. Devido às especificidades do algoritmo, vou oferecer minha própria versão. Como queremos verificar as 4 gons para a condição de Delaunay, consideramos sua estrutura. Cada quadrângulo em triangulação é de 2 triângulos com uma aresta comum. Cada aresta tem exatamente 2 triângulos adjacentes. Assim, cada quadrângulo em triangulação é gerado por uma aresta e dois vértices opostos à aresta em triângulos adjacentes.
Como dois triângulos e sua adjacência são restaurados ao longo da aresta e dois vértices, podemos restaurar a triangulação para todas essas estruturas. Assim, propõe-se armazenar uma aresta com dois vértices no conjunto e realizar uma pesquisa ao longo da aresta (um par de vértices ordenados).

Algoritmo

A idéia da linha de varredura é que todos os pontos sejam classificados em uma direção e depois processados ​​por sua vez.

1. Classifique todos os pontos em uma linha reta (por simplicidade, por coordenadas $$$x$)
2. Construímos um triângulo nos 3 primeiros pontos.
   
   Além disso, para cada próximo ponto, executaremos etapas que preservam a invariante de que existe uma triangulação em Delaunay para pontos já adicionados e, consequentemente, um MBO para eles.
3. Adicione os triângulos formados pelas arestas visíveis e pelo próprio ponto (ou seja, adicione as arestas do ponto em questão a todas as extremidades das arestas visíveis).
4. Verificamos na condição de Delaunay todos os quadrângulos gerados pelas arestas visíveis. Se em algum lugar a condição não for atendida, reconstruímos a triangulação no quadrilátero (lembro-me de que existem apenas dois deles) e executamos recursivamente a verificação dos quadriláteros gerados pelas bordas do quadrilátero atual (porque somente depois deles a condição de Delaunay poderia ser violada).

Nota : na etapa (4) durante uma partida recursiva, não é possível verificar os quadrângulos gerados pelas arestas provenientes do ponto considerado nesta iteração (sempre existem duas em cada quatro). Na maioria das vezes eles serão não convexos, pois convexa a prova é puramente geométrica, deixarei para o leitor. Além disso, assumimos que apenas 2 partidas recursivas são executadas para cada reconstrução.

Verificando uma condição de Delaunay

Formas de testar quadrângulos para a condição de Delaunay podem ser encontradas no mesmo livro [1]. Observo apenas que, ao escolher um método com funções trigonométricas a partir daí, com implementação imprecisa, valores negativos de senos podem ser obtidos, faz sentido levá-los ao módulo.

Procure arestas visíveis

Resta entender como encontrar efetivamente arestas visíveis. Observe que o ponto adicionado anterior S está no MBO na iteração atual, pois possui a maior coordenada $$$x$e também é visível para o ponto atual. Depois, observando que as extremidades das arestas visíveis formam uma cadeia contínua de pontos visíveis, podemos ir do ponto S em ambas as direções ao longo do MBO e coletar as arestas enquanto estão visíveis (a visibilidade da aresta é verificada usando o produto vetorial). Portanto, é conveniente armazenar o MBO como uma lista duplamente conectada, a cada iteração, removendo as arestas visíveis e adicionando 2 novas a partir do ponto considerado.

Visualização de algoritmo

Dois pontos vermelhos - adicionados e anteriores. Bordas vermelhas a cada momento compõem a pilha de recursão da etapa (4):

Correção do algoritmo

Para provar a correção do algoritmo, basta provar a conservação do invariante nas etapas (3) e (4).

Etapa (3)

Após o passo (3), obviamente, obtemos alguma triangulação do atual conjunto de pontos.

Etapa (4)

No processo da etapa (4), todos os quadrângulos que não satisfazem a condição de Delaunay estão na pilha de recursão (segue a descrição), o que significa que no final da etapa (4) todos os quadrângulos satisfazem a condição de Delaunay, ou seja, a triangulação de Delaunay é realmente construída. Então resta provar que o processo na etapa (4) terminará algum dia. Isso decorre do fato de que todas as arestas adicionadas durante a reconstrução vêm do vértice atual em questão (ou seja, na etapa $$$k$não há mais do que $$$k-1$) e do fato de que, depois de adicionar essas arestas, não consideraremos os quadrângulos gerados por elas (veja a observação anterior), o que significa que não adicionaremos mais de uma vez.

Complexidade do tempo

Em média, o algoritmo funciona muito bem em distribuições uniformes e normais (os resultados são mostrados na tabela abaixo). Supõe-se que seu tempo de trabalho seja $$$O (NlogN)$. No pior dos casos, uma avaliação ocorre $$$O (N ^ 2)$.

Vamos dar uma olhada no tempo de trabalho em partes e entender qual deles tem o maior impacto no tempo total:

Classificar por direção

Para classificação, usaremos a estimativa $$$O (NlogN)$.

Procure arestas visíveis

Primeiro, mostramos que o tempo total gasto na busca de bordas visíveis é $$$O (N)$. Observe que a cada iteração encontramos todas as arestas visíveis e mais 2 (primeiro não visíveis) em tempo linear. Na etapa (3), adicionamos novas 2 arestas ao MBO. Assim, no total, não mais que $$$2N$costelas, portanto, e várias costelas visíveis não serão mais $$$2N$. Também vamos encontrar $$$2N$arestas que não são visíveis. Assim, no total, não há mais $$$4N$costelas que correspondem ao tempo $$$O (N)$.

Construindo novos triângulos

O tempo total para a construção de triângulos do passo (3) com arestas visíveis já encontradas é obviamente $$$O (N)$.

Reconstruindo a triangulação

Resta lidar com a etapa (4). Primeiro, observe que verificar a condição de Delaunay e reconstruir se ela não for atendida são ações bastante caras (embora funcionem para $$$O (1)$) Somente ao verificar a condição de Delaunay, são necessárias cerca de 28 operações aritméticas. Vejamos o número médio de reconstruções durante esta etapa. Os resultados práticos de algumas distribuições são apresentados abaixo. Para eles, quero realmente dizer que o número médio de rearranjos cresce com uma velocidade logarítmica, mas vamos deixar isso como uma suposição.

Aqui também quero observar que o número médio de rearranjos por ponto pode variar muito da direção na qual a classificação é realizada. Portanto, para um milhão distribuído uniformemente em um retângulo baixo longo com uma proporção de 100000: 1, esse número varia de 1,2 a 24 (esses valores são alcançados ao classificar os dados horizontal e verticalmente, respectivamente). Portanto, vejo o ponto de escolher a direção da classificação de maneira arbitrária (neste exemplo, com seleção arbitrária, em média, foram obtidas cerca de 2 reconstruções) ou selecioná-la manualmente se os dados forem conhecidos antecipadamente.

Assim, o tempo principal que o programa normalmente leva para a etapa (4). Se for executado rapidamente, faz sentido pensar em acelerar a classificação.

Pior caso

Pior caso em $$$k$a iteração ocorre $$$k-1$a chamada recursiva na etapa (4), ou seja, somando todo i, obtemos o comportamento assintótico no pior caso $$$O (N ^ 2)$. A figura a seguir ilustra um belo exemplo no qual o programa pode funcionar por muito tempo (1100 recria em média ao adicionar um novo ponto com uma entrada de 10.000 pontos).

Comparação com um algoritmo iterativo para construir uma triangulação de Delaunay usando kD-tree

Descrição do algoritmo iterativo

Descreverei brevemente o algoritmo acima. Quando chega o próximo ponto, usamos a árvore kD (eu aconselho você a ler sobre isso em algum lugar, se você não souber), encontramos um triângulo que já está bem próximo a ele. Contornando em profundidade, procuramos um triângulo, no qual o ponto em si cai. Estendemos as arestas aos vértices do triângulo encontrado e, na verdade, executamos a etapa (4) do nosso algoritmo para os novos quadrângulos. Como o ponto pode estar fora da triangulação, para simplificação, propõe-se cobrir todos os pontos com um triângulo grande (para construí-lo antecipadamente), isso resolverá o problema.

Similaridade de algoritmos

De fato, se pontos são adicionados em ordem classificada em direção, então nosso algoritmo funciona da mesma forma que iterativo, exceto que o número de rearranjos é menor. A animação a seguir demonstra isso perfeitamente. Nela, foram adicionados pontos da direita para a esquerda e todos são cobertos por um grande triângulo, que é posteriormente removido.

Diferenças de algoritmo

Em um algoritmo iterativo, a localização de um ponto (busca pelo triângulo desejado) ocorre em média acima de $$$O (logN)$, nas distribuições acima, ocorrem, em média, três rearranjos (como mostrado em [1]) sob a condição de uma ordem arbitrária de fornecimento de pontos. Assim, a linha de varredura ganha o tempo do algoritmo iterativo na localização, mas perde na reconstrução (o que, lembro-me, é bastante difícil). Além disso, o algoritmo iterativo funciona on-line, que também é seu recurso distintivo.

Conclusão

Aqui apenas mostro algumas triangulações interessantes resultantes da operação do algoritmo.

Belo padrão

Distribuição normal, 1000 pontos

Distribuição uniforme, 1000 pontos

Triangulação construída nas localizações de todas as cidades da Rússia

Aqui você pode ver um exemplo do meu código para este algoritmo:
github.com/Vemmy124/Delaunay-Triangulation-Algorithm

Obrigado pela atenção!

Literatura

[1] Skvortsov A.V. Triangulação de Delaunay e sua aplicação. - Tomsk: Editora Tom. Universidade, 2002 - 128 p. ISBN 5-7511-1501-5