Estamos envolvidos na compra de tráfego do Adwords (uma plataforma de publicidade do Google). Uma das tarefas regulares nesta área é a criação de novos banners. Os testes mostram que os banners perdem eficácia com o tempo, à medida que os usuários se acostumam; As estações e as tendências estão mudando. Além disso, temos o objetivo de capturar diferentes nichos de público, e os banners segmentados por pouco funcionam melhor.

Em conexão com a entrada de novos países, surgiu a questão da localização de banners. Para cada banner, você precisa criar versões em diferentes idiomas e com moedas diferentes. Você pode solicitar que os designers façam isso, mas este trabalho manual adicionará uma carga adicional a um recurso já escasso.

Parece uma tarefa fácil de automatizar. Para isso, basta criar um programa que imponha no banner um preço localizado para o "preço" e apelo à ação (frase como "compre agora") no botão. Se a impressão de um texto em uma imagem é bastante simples, determinar onde você deve colocá-lo nem sempre é trivial. Peppercorns acrescenta que o botão vem em cores diferentes e tem uma forma ligeiramente diferente.

Este artigo é dedicado a: como encontrar o objeto especificado na imagem? Métodos populares serão resolvidos; Áreas de aplicação, recursos, prós e contras. Os métodos acima podem ser usados ​​para outros fins: desenvolvimento de programas para câmeras de segurança, automação da interface do usuário de teste e similares. As dificuldades descritas podem ser encontradas em outras tarefas e os métodos utilizados podem ser usados ​​para outros fins. Por exemplo, o Canny Edge Detector é freqüentemente usado para pré-processar imagens, e o número de pontos-chave pode ser usado para avaliar a "complexidade" visual de uma imagem.

Espero que as soluções descritas reponham seu arsenal de ferramentas e truques para resolver problemas.

O código está no Python 3.6 ( repositório ); Biblioteca OpenCV necessária. O leitor deve entender os conceitos básicos de álgebra linear e visão computacional.

Vamos nos concentrar em encontrar o botão em si. Lembraremos de encontrar etiquetas de preço (já que encontrar um retângulo também pode ser resolvido de maneiras mais simples), mas omiti-lo, pois a solução terá a mesma aparência.

Correspondência de modelos

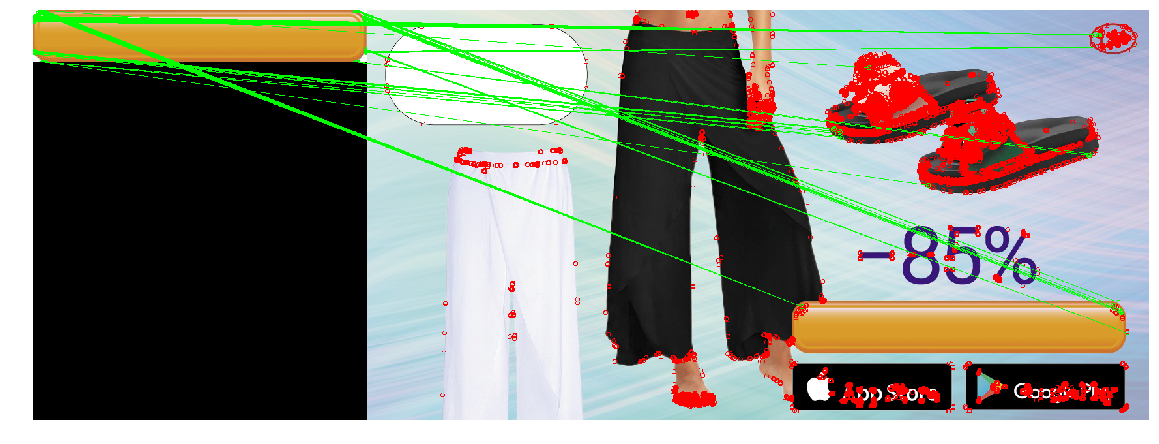
O primeiro pensamento que vem à mente é por que não escolher e encontrar na imagem a região que é mais semelhante ao botão em termos de diferença de cor dos pixels? É isso que faz a correspondência de modelos - um método baseado em encontrar espaço na imagem que é mais semelhante ao modelo. A "semelhança" de uma imagem é definida por uma métrica específica. Ou seja, o modelo é “sobreposto” na imagem e a discrepância entre a imagem e o modelo é considerada. A posição do modelo em que essa discrepância será mínima e indicará a localização do objeto desejado.

Você pode usar opções diferentes como métrica, por exemplo, a soma das diferenças ao quadrado entre um modelo e uma imagem (soma das diferenças ao quadrado, SSD) ou usar a correlação cruzada (CCORR). Seja f e g a imagem e o padrão com as dimensões (k, l) e (m, n), respectivamente (ignoraremos os canais de cores por enquanto); i, j - posição na imagem à qual "anexamos" o modelo.

$$

$$SSD_ {i, j} = \ sum_ {a = 0..m, b = 0..n} {(f_ {i + a, j + b} - g_ {a, b}) ^ 2}$$

$$

$$CCORR_ {i, j} = \ sum_ {a = 0..m, b = 0..n} {(f_ {i + a, j + b} \ cdot g_ {a, b}) ^ 2}$$

Vamos tentar aplicar a diferença de quadrados para encontrar um gatinho

Na foto

(foto tirada da PETA Caring for Cats).

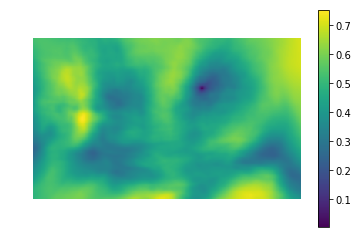
A imagem da esquerda é o valor métrico da semelhança do local na imagem com o modelo (ou seja, os valores de SSD para diferentes i, j). A área escura é o lugar onde a diferença é mínima. Este é um ponteiro para o local que mais se assemelha a um modelo - na figura à direita, este local é circulado.

A correlação cruzada é na verdade uma convolução de duas imagens. Convoluções podem ser implementadas rapidamente usando a rápida transformação de Fourier. De acordo com o teorema da convolução, após a transformação de Fourier, a convolução se transforma em uma multiplicação elementar simples:

$$

$$CCORR_ {i, j} = f \ circledast g = IFFT (FFT (f \ circledast g)) = IFFT (FFT (f) \ cdot FFT (g))$$

Onde $$$\ circledast$ - operador de convolução. Dessa forma, podemos calcular rapidamente a correlação cruzada. Isso fornece a complexidade geral de O (kllog (kl) + mnlog (mn)) versus O (klmn) quando implementado de frente. O quadrado da diferença também pode ser realizado por convolução, pois após abrir os colchetes, ele se transformará na diferença entre a soma dos quadrados dos valores de pixel da imagem e a correlação cruzada:

$$

$$SSD_ {i, j} = \ sum_ {a = 0..m, b = 0..n} {(f_ {i + a, j + b} - g_ {a, b}) ^ 2} =$$

$$

$$= \ sum_ {a = 0..m, b = 0..n} {f_ {i + a, j + b} ^ 2 - 2 f_ {i + a, j + b} g_ {a, b} + g_ {a, b} ^ 2} =$$

$$

$$= \ sum_ {a = 0..m, b = 0..n} {f_ {i + a, j + b} ^ 2 + g_ {a, b} ^ 2} - 2CCOR_ {i, j}$$

Detalhes podem ser vistos nesta apresentação .

Vamos para a implementação. Felizmente, colegas do departamento Nizhny Novgorod Intel cuidaram de nós ao criar a biblioteca OpenCV, ele já implementa uma pesquisa por um modelo usando o método matchTemplate (a propósito, ele usa a implementação da FFT, embora isso não seja mencionado na documentação), usando diferentes métricas de discrepância :

• CV_TM_SQDIFF - a soma dos quadrados da diferença nos valores de pixel
• CV_TM_SQDIFF_NORMED - a soma do quadrado das diferenças de cores, normalizada para o intervalo 0..1.
• CV_TM_CCORR - a soma dos produtos elemento a elemento do segmento de modelo e imagem
• CV_TM_CCORR_NORMED - a soma do elemento funciona, normalizada no intervalo -1..1.
• CV_TM_CCOEFF - correlação cruzada de imagens sem média
• CV_TM_CCOEFF_NORMED - correlação cruzada entre imagens sem média, normalizada para -1..1 (correlação de Pearson)

Vamos usá-los para encontrar um gatinho:

Pode-se observar que apenas o TM_CCORR não lidou com sua tarefa. Isso é compreensível: como é um produto escalar, o maior valor dessa métrica será ao comparar um modelo com um retângulo branco.

Você pode perceber que essas métricas exigem a correspondência de padrões pixel por pixel na imagem desejada. Qualquer desvio de gama, luz ou tamanho resultará em métodos não funcionando. Deixe-me lembrá-lo de que esse é exatamente o nosso caso: os botões podem ter tamanhos e cores diferentes.

O problema de cores e luzes diferentes pode ser resolvido aplicando um filtro de detecção de borda. Esse método deixa apenas informações sobre onde na imagem houve mudanças nítidas de cor. Vamos aplicar o Canny Edge Detector (vamos analisá-lo um pouco mais) nos botões de diferentes cores e brilho. À esquerda, os banners originais e à direita, o resultado da aplicação do filtro Canny.

No nosso caso, também há um problema de tamanhos diferentes, mas ele já foi resolvido. A transformação log-polar transforma uma imagem em um espaço no qual o zoom e a rotação aparecerão como um deslocamento. Usando essa transformação, podemos restaurar a escala e o ângulo. Depois disso, ao dimensionar e girar o modelo, você pode encontrar a posição do modelo na imagem original. Você também pode usar a FFT em todo este procedimento, conforme descrito em Uma técnica baseada em FFT para tradução, rotação e registro de imagens invariáveis ​​em escala . Na literatura, o caso é considerado quando os padrões horizontal e vertical são alterados proporcionalmente, enquanto o fator de escala varia dentro de pequenos limites (2,0 ... 0,8). Infelizmente, o redimensionamento de um botão pode ser grande e desproporcional, o que pode levar a um resultado incorreto.

Aplicamos a construção resultante (filtro Canny, restaurando apenas a escala através da transformação log-polar, obtendo a posição através da localização do local com a discrepância quadrática mínima), para encontrar o botão em três figuras. Usaremos o grande botão amarelo como modelo:

Ao mesmo tempo, os botões nos banners serão de diferentes tipos, cores e tamanhos:

No caso de redimensionar o botão, o método não funcionou corretamente. Isso se deve ao fato de o método envolver o redimensionamento de botões no mesmo número de vezes na horizontal e na vertical. No entanto, esse nem sempre é o caso. Na imagem certa, o tamanho do botão não mudou na vertical, mas na horizontal diminuiu bastante. Se o redimensionamento for muito grande, as distorções causadas pela transformação log-polar tornam a pesquisa instável. Nesse sentido, o método não pôde detectar o botão no terceiro caso.

Detecção de ponto-chave

Você pode tentar uma abordagem diferente: em vez de procurar o botão inteiro, vamos encontrar suas partes típicas, por exemplo, os cantos do botão ou os elementos da borda (há um traço decorativo ao longo do contorno do botão). Parece que encontrar cantos e bordas é mais fácil, pois esses são objetos pequenos (e, portanto, simples). O que fica entre os quatro cantos e a borda será um botão. A classe de métodos para encontrar pontos-chave é chamada “detecção de ponto-chave”, e os algoritmos para comparar e procurar imagens usando pontos-chave são chamados “correspondência de ponto-chave”. A pesquisa de um padrão em uma imagem reduz a aplicação de um algoritmo para detectar pontos-chave em um padrão e em uma imagem e a comparação de pontos-chave de um padrão e uma imagem.

Normalmente, os "pontos-chave" são automaticamente encontrados ao encontrar pixels cujo ambiente possui determinadas propriedades. Muitos métodos e critérios para encontrá-los foram inventados. Todos esses algoritmos são heurísticas que encontram alguns elementos característicos da imagem, como ângulos de regra ou mudanças nítidas de cor. Um bom detector deve funcionar rapidamente e ser resistente a transformações de imagem (ao alterar a imagem, os pontos principais não devem deixar de ser / se mover).

Harris corner detector

Um dos algoritmos mais básicos é o detector de canto Harris . Para a foto (daqui em diante consideramos que estamos operando com “intensidade” - uma imagem traduzida em escala de cinza), ele tenta encontrar pontos nas proximidades dos quais as diferenças de intensidade são maiores que um determinado limite. O algoritmo é assim:

1. De intensidade $$$I$ são derivadas ao longo dos eixos x e y ( $$$I_x$ e $$$I_y$ respectivamente). Eles podem ser encontrados, por exemplo, aplicando o filtro Sobel.

   
   

2. Para um pixel, considere o quadrado $$$I_x$ quadrado $$$I_y$ e trabalha $$$I_x$ e $$$I_y$ . Algumas fontes os rotulam como $$$I_ {xx}$ , $$$I_ {xy}$ e $$$I_ {xy}$ - o que não acrescenta clareza, pois se pode pensar que essas são as segundas derivadas da intensidade (e não é assim).

   
   

3. Para cada pixel, consideramos as somas em um determinado bairro (mais de 1 pixel) com as seguintes características:

   $$

   $$A = \ sum_ {x, y} {w (x, y) I_xI_x}$$
   
   

   $$

   $$B = \ sum_ {x, y} {w (x, y) I_xI_y}$$
   
   

   $$

   $$C = \ sum_ {x, y} {w (x, y) I_yI_y}$$
   
   Como na Detecção de gabarito, esse procedimento para janelas grandes pode ser realizado com eficiência usando o teorema da convolução.
   

4. Para cada pixel, calcule o valor $$$^ \ estrela$ heurística R

   $$

   $$R = Det (H) - k (Tr (H)) ^ 2 = (AB - C ^ 2) - k (A + B) ^ 2$$
   
   Valor $$$k$ selecionado empiricamente no intervalo [0,04, 0,06] $$$R$ algum pixel tem um certo limite, então a vizinhança $$$w$ esse pixel contém um ângulo e o marcamos como um ponto-chave.
   

5. A fórmula anterior pode criar agrupamentos de pontos-chave próximos um do outro, caso em que vale a pena removê-los. Isso pode ser feito verificando para cada ponto se ele tem um valor $$$R$ máximo entre vizinhos imediatos. Caso contrário, o ponto principal é filtrado. Este procedimento é chamado de supressão não máxima .

   
   

$$$\ estrela$ Formula $$$R$ então escolhido por uma razão. $$$A, B, C$ - componentes do tensor estrutural - matriz que descreve o comportamento do gradiente na vizinhança:

$$

$$H = \ begin {pmatrix} A & C \\ C & B \ end {pmatrix}$$

Essa matriz é semelhante em muitos aspectos à sua matriz de covariância. Por exemplo, ambas são matrizes positivamente semidefinidas, mas a semelhança não se limita a isso. Deixe-me lembrá-lo de que a matriz de covariância possui uma interpretação geométrica. Os autovetores da matriz de covariância indicam as direções da maior variância dos dados de origem (nos quais a covariância foi calculada), e os autovalores indicam a dispersão ao longo do eixo:

Imagem retirada de http://www.visiondummy.com/2014/04/geometric-interpretation-covariance-matrix/

Os autovalores do tensor estrutural também se comportam da mesma maneira: descrevem a dispersão dos gradientes. Em uma superfície plana, os valores próprios do tensor estrutural serão pequenos (porque a dispersão dos gradientes em si será pequena). Os autovalores do tensor estrutural construído em uma parte de uma imagem com uma face variam muito: um número será grande (e corresponderá ao seu próprio vetor direcionado perpendicularmente à face) e o segundo será pequeno. No tensor angular, os dois valores próprios serão grandes. Com base nisso, podemos criar uma heurística ( $$$\ lambda_1, \ lambda_2$ São os autovalores do tensor estrutural).

$$

$$R = \ lambda_1 \ lambda_2 - k (\ lambda_1 + \ lambda_2) ^ 2$$

O valor dessa heurística será grande quando os dois valores próprios forem grandes.

A soma dos valores próprios é o traço da matriz, que pode ser calculada como a soma dos elementos na diagonal (e se você observar as fórmulas A e B, fica claro que essa também é a soma dos quadrados dos comprimentos dos gradientes na região):

$$

$$\ lambda_1 + \ lambda_2 = Tr (H) = A + B$$

O produto de autovalores é o determinante de uma matriz, que também é fácil de escrever no caso de 2x2:

$$

$$\ lambda_1 \ lambda_2 = Det (H) = AB - C ^ 2$$

Assim, podemos calcular efetivamente $$$R$ , expressando-o em termos dos componentes do tensor estrutural.

Rápido

O método de Harris é bom, mas existem muitas alternativas. Não consideraremos tudo da mesma maneira que o método acima, mencionaremos apenas alguns populares para mostrar truques interessantes e compará-los em ação.

Pixels verificados pelo algoritmo FAST

Uma alternativa ao método de Harris é o FAST . Como o nome sugere, o FAST é muito mais rápido que o método acima. Esse algoritmo tenta encontrar os pontos que ficam nas bordas e nos cantos dos objetos, ou seja, em lugares de diferença de contraste. Sua localização é a seguinte: FAST constrói um círculo de raio R em torno do pixel candidato e verifica se ele possui um segmento contínuo de pixels de comprimento t que é mais escuro (ou mais claro) do pixel candidato por K unidades. Se essa condição for atendida, o pixel será considerado um "ponto chave". Para certos t, podemos implementar essa heurística com eficiência, adicionando algumas verificações preliminares que cortam os pixels que são garantidos como não-cantos. Por exemplo, quando $$$R = 3$ e $$$t = 12$ , basta verificar se há 3 pixels consecutivos entre os 4 pixels extremos que são estritamente mais escuros / claros que o centro de K (na imagem - 1, 5, 9, 13). Essa condição permite excluir efetivamente os candidatos que definitivamente não são pontos-chave.

SIFT

Ambos os algoritmos anteriores não são resistentes ao redimensionamento da imagem. Eles não permitem encontrar um modelo na imagem se a escala do objeto tiver sido alterada. SIFT (transformação de recurso invariável em escala) oferece uma solução para esse problema. Pegue a imagem da qual extraímos os pontos-chave e comece a reduzir gradualmente seu tamanho com um pequeno passo, e para cada opção de escala, encontraremos os pontos-chave. Escalar é um procedimento difícil, mas reduzi-lo em 2/4/8 / ... vezes pode ser feito com eficiência pulando pixels (no SIFT, essas múltiplas escalas são chamadas de "oitavas"). As escalas intermediárias podem ser aproximadas aplicando um bluer gaussiano com um tamanho de núcleo diferente à imagem. Como descrito acima, isso pode ser feito computacionalmente com eficiência. O resultado será parecido se primeiro reduzíssemos a imagem e a ampliassemos para o tamanho original - pequenos detalhes são perdidos, a imagem fica "borrada".

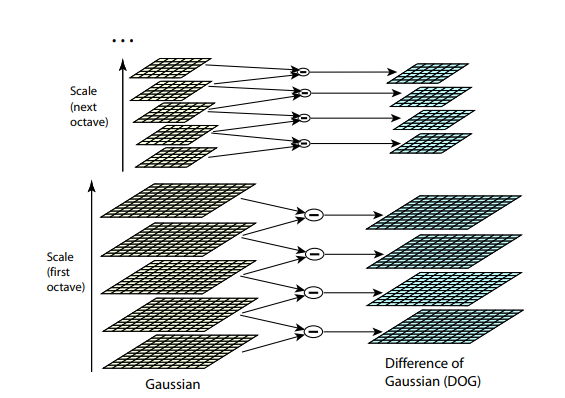
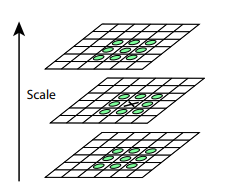
Após este procedimento, calculamos a diferença entre escalas vizinhas. Valores grandes (em valor absoluto) nessa diferença resultarão se alguns pequenos detalhes deixarem de ser visíveis no próximo nível de escala ou, inversamente, o próximo nível de escala começará a capturar uma parte que não era visível no anterior. Essa técnica é chamada de Dog, Diferença de Gaussiana. Podemos supor que a grande importância dessa diferença já é um sinal de que há algo interessante neste local na imagem. Mas estamos interessados ​​na escala em que esse ponto-chave será mais expressivo. Para fazer isso, consideraremos um ponto-chave não apenas como um ponto que difere de seus arredores, mas também que difere mais fortemente entre diferentes escalas de imagem. Em outras palavras, escolheremos um ponto-chave não apenas no espaço X e Y, mas no espaço $$$(X, Y, Escala)$ . No SIFT, isso é feito encontrando pontos no DoG (Diferença de Gaussianos), que são altos ou baixos locais em $$$3x3x3$ cubo de espaço $$$(X, Y, Escala)$ ao seu redor:

Algoritmos para encontrar pontos-chave e construir descritores SIFT e SURF são patenteados. Ou seja, para uso comercial é necessário obter uma licença. É por isso que eles não estão disponíveis no pacote opencv principal, mas apenas em um pacote opencv_contrib separado. No entanto, até agora nossa pesquisa é puramente acadêmica por natureza, portanto, nada nos impede de participar do SIFT em comparação.

Descritores

Vamos tentar aplicar algum tipo de detector (por exemplo, Harris) ao modelo e à imagem.

Depois de encontrar os pontos principais na figura e no modelo, é necessário compará-los de alguma forma. Deixe-me lembrá-lo que até agora extraímos apenas as posições dos pontos-chave. O que esse ponto significa (por exemplo, em qual direção o ângulo encontrado é direcionado), ainda não determinamos. E essa descrição pode ajudar ao comparar pontos e padrões de imagem entre si. Alguns dos pontos do modelo na imagem podem ser alterados por distorções, cobertas por outros objetos, portanto confiar apenas na posição dos pontos em relação um ao outro parece não confiável. Portanto, vamos dar uma vizinhança para cada ponto-chave para criar uma certa descrição (descritor), o que nos permite pegar alguns pontos (um ponto do modelo, um da imagem) e comparar sua semelhança.

BREVE

(.. 0 1), , XOR , . ? , N . , i- , , — i- 1. N. - (, — ), : , “”. , ( ). BRIEF .

. . , GII .

, , (.. , , ). OpenCV .

SIFT

SIFT , . SIFT 1616 , 44 . ( , ). 8 (, -, , ..). — 8 , , . . , 8- . 128 ( 4*4 = 16 , 8 ). .

Comparação

( — , ), - :

— . ?

, . , , . , , , , . ? BRIEF, , , . , BRIEF 1/16 . SIFT — - 1/4 .

SIFT.

Agora aplicamos todo o conhecimento adquirido para resolver nosso problema. No nosso caso, os requisitos para o detector de ponto-chave são suficientes: não precisamos de invariância para redimensionar, além de desempenho extremamente alto. Compare todos os três detectores.

Harris corner detector	Rápido	SIFT

SIFT encontrou extremamente poucos pontos-chave no botão. Isso é compreensível - o botão é um objeto bastante pequeno e plano, e o zoom não ajuda a encontrar pontos-chave.

Além disso, nem um único detector gerenciava o terceiro caso. Isso é explicável e esperado. Normalmente, os métodos acima são usados ​​para encontrar um objeto de um modelo em uma imagem onde ele pode ser parcialmente oculto, girado ou ligeiramente distorcido. No nosso caso, queremos encontrar não exatamente o mesmo objeto , mas um objeto que seja bastante semelhante ao modelo (botão) . Esta é uma tarefa ligeiramente diferente. Portanto, alterar a forma do botão em si (por exemplo, o raio de arredondamento dos cantos ou a espessura da moldura dos pontos) altera os pontos principais neles e seus descritores. Além disso, os pontos principais estarão localizados no canto do botão. Devido à posição na borda, os pontos serão instáveis: sua localização exata e descritores são afetados pelo que é desenhado ao lado do botão.

Conclusão - o método é bom e atende corretamente a situações em que o objeto desejado é girado, seu tamanho é alterado ou o objeto é parcialmente oculto (o que é bom para encontrar objetos complexos ou um preço, por exemplo). No entanto, se houver poucos pontos no objeto que possam ser "capturados" ou a forma do objeto mudar muito, os pontos principais e eles no modelo e na imagem poderão não coincidir. Além disso, um plano de fundo com muitos pequenos detalhes pode mudar os "pontos-chave" ou alterar seus descritores.

Podemos criar uma correspondência que use as coordenadas dos pontos principais. Em vez de procurar pares de pontos no modelo e na imagem, cuja vizinhança é semelhante, você pode procurar por esses conjuntos de pontos, a interposição dos pontos-chave no modelo e na imagem será semelhante. No caso geral, essa é uma tarefa bastante complicada (tanto computacional quanto do ponto de vista da programação), especialmente em uma situação em que alguns pontos podem ser alterados ou ausentes. Mas, dado que temos pontos-ângulos-chave, é suficiente encontrarmos grupos que formarão aproximadamente um retângulo das proporções desejadas e dentro dos quais não haverá pontos-chave. Gradualmente, chegamos ao seguinte método:

Detecção de contorno

Normalmente, um botão é algum tipo de objeto retangular (às vezes com cantos arredondados), cujos lados são paralelos aos eixos das coordenadas. Então, vamos tentar distinguir as zonas de diferença de contraste (arestas) e, entre elas, encontraremos faces cujos contornos são semelhantes ao contorno do objeto de que precisamos. Este método é chamado detecção de contorno.

Detecção de borda

Ao contrário da detecção de ponto-chave, estamos interessados ​​não apenas em ângulos de ponto-chave, mas também em arestas. No entanto, as idéias básicas que podemos tirar daí. Alise a imagem com um filtro gaussiano e como no detector de canto Harris. Então calculamos as derivadas da intensidade $$$I_x$ e $$$I_y$ . Como não precisamos distinguir ângulos de arestas, não precisamos considerar o tensor estrutural - basta calcular a força do gradiente: $$$I_l = I_x ^ 2 + I_y ^ 2$ (a propósito, essa é a raiz do $$$Tr (H)$ ou da soma da diagonal do tensor estrutural). Depois disso, deixamos apenas os pixels que são máximos locais em termos de $$$I_l$ (usando a supressão não máxima já considerada), mas como local, escolheremos não 8 pixels vizinhos, mas esses pixels desses 8, para os quais eu estou direcionado, e do lado oposto:

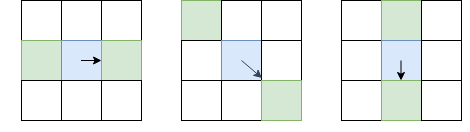
O pixel em questão é azul, a seta é a direção I. Os pixels verdes são aqueles que serão levados em consideração durante a supressão não máxima.

Uma escolha tão incomum de pixels para comparação se deve ao fato de que não queremos abrir espaços na borda. Na figura da esquerda, a face vai de cima para baixo e, como a supressão não máxima não compara as intensidades com os pixels acima e abaixo do azul, obtemos uma face contínua.

Obviamente, uma supressão não máxima não é suficiente, e você precisa aplicar algum tipo de filtragem para remover arestas com um valor muito baixo de IL. Para fazer isso, aplicamos a técnica de “duplo limiar”: removemos todos os pixels com Il, com uma intensidade de gradiente abaixo do limiar baixo, e atribuímos todos os pixels acima do limiar alto como “bordas fortes”. Os pixels nos quais a intensidade do gradiente se encontra entre Baixa e Alta serão chamados de "bordas fracas"; só os deixamos se estiverem conectados a "bordas fortes":

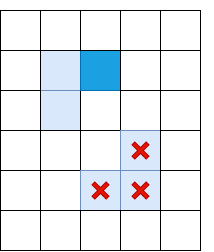
Azul claro indica "costelas fracas", azul escuro - forte. As nervuras na parte inferior são peneiradas, uma vez que não estão conectadas a nenhuma nervura forte.

Acabamos de descrever o Canny Edge Detector. É amplamente utilizado até hoje como um procedimento simples e rápido que permite encontrar os contornos dos objetos.

Rastreamento de fronteira

A próxima ação é selecionar os contornos no mapa com as faces encontradas. Encontre os componentes relacionados (ilhas de pixels adjacentes que passaram em todas as verificações) e verifique cada um deles quanto parece um botão. Depois de aplicar a supressão não máxima no Canny, temos garantias de que as bordas terão um pixel de espessura, mas vamos confiar nisso. Para cada pixel que foi atribuído a uma face e próximo ao qual existe um pixel sem face, atribuímos a uma "borda". Movendo-se de um pixel da borda para outro, voltamos ao mesmo pixel (e encontramos o caminho) ou a um beco sem saída (então você pode tentar voltar se houver uma bifurcação em algum lugar ao longo do caminho):

O algoritmo de rastreamento de borda completa, levando em consideração diferentes casos de borda (por exemplo, quando um objeto com uma face espessa gerou dois contornos, interno e externo), é descrito aqui . Depois de aplicar esse algoritmo, teremos um conjunto de contornos que podem ser botões.

Filtragem de caminho

Como saber que nosso circuito é um botão? Para retângulos e polígonos, existe um excelente método baseado na simplificação do contorno . É o suficiente para "desmoronar" gradualmente as costelas, se estiverem quase em linha reta, e depois calcular o número de costelas restantes e verificar os ângulos entre elas. Infelizmente, para o nosso caso, esses métodos não são adequados - nosso retângulo possui cantos arredondados. Além disso, há correspondência de contorno para figuras com geometria complexa - mas isso também não é sobre nós, pois temos apenas um retângulo (exemplos com um esboço humano são dados no artigo). Portanto, é melhor criar um filtro com base nas propriedades da própria figura. Sabemos que:

• O botão é grande o suficiente (área com mais de 100 pixels)
• Os lados são paralelos aos eixos de coordenadas
• A proporção da área da figura para a área do retângulo delimitador deve estar bastante próxima da unidade. Definimos o limite como 0,8, pois o botão é um retângulo com lados paralelos aos eixos das coordenadas e os 20% ausentes são os cantos arredondados.

Além disso, a partir da experiência de usar detectores de ponto principal, lembramos que pode haver problemas com situações em que há um objeto de contraste sob o botão. Portanto, depois de aplicar o Canny, desfocamos as bordas para fechar pequenos orifícios que possam surgir desses objetos.

Aplicamos a abordagem resultante:

O aplicativo de filtro Canny (figura 2) encontrou a forma necessária, mas devido à forma complexa do botão e ao gradiente, muitos contornos foram encontrados ao mesmo tempo e, devido à supressão não máxima, alguns deles não foram fechados. A aplicação de desfoque (3 fotos) resolveu o problema.

Abordagem de teste

Execute a pesquisa de contornos na imagem resultante. Pinte os contornos que passaram no teste em vermelho. Se houver vários deles, precisamos escolher a opção mais bem-sucedida entre eles. Selecionamos o contorno da maior área e pintamos em verde.

| | | |

O design resultante encontrou botões nas imagens de teste. Uma execução em todos os banners mostrou que, ocasionalmente (1 caso entre ~ 20), em vez de um botão, ele seleciona dados retangulares da iOS Appstore e Google Apps, ou outros objetos retangulares (casos de telefone). Portanto, adicionando a capacidade de indicar manualmente a posição naquele raro caso de uma determinação incorreta, implementamos essa opção na ferramenta de localização.

Conclusão

Para resumir. O currículo “clássico” sem aprendizado profundo ainda funciona e, com base nele, você pode resolver problemas. Eles são despretensiosos e não requerem uma grande quantidade de dados marcados, hardware poderoso e são mais fáceis de depurar. No entanto, eles introduzem suposições adicionais e, portanto, com a ajuda deles, nem todos os problemas podem ser resolvidos com eficácia.

• A correspondência de modelo é a maneira mais fácil, com base na localização de um local na imagem que seja mais semelhante (por alguma métrica simples) a um modelo. Eficaz com correspondência pixel por pixel. Pode ser resistente a dobras e pequenas alterações de tamanho, mas com grandes alterações pode não funcionar corretamente.
• Detecção / correspondência de ponto-chave - encontre os pontos-chave, os pontos da imagem e o modelo. Os detectores são resistentes a rotações, zoom (dependendo do detector e descritor selecionado) e coincidem - com sobreposições parciais. Mas esse método funciona bem apenas se houver "pontos-chave" suficientes no objeto, e as localidades dos pontos do modelo e da imagem coincidem muito bem (ou seja, o mesmo objeto no modelo e na imagem).
• Detecção de contorno - localizando os contornos dos objetos e localizando um contorno semelhante ao contorno do objeto desejado. Essa solução leva em consideração apenas a forma do objeto e ignora seu conteúdo e cor (que podem ser tanto um mais quanto um menos).
  Um leitor experiente pode perceber que nosso problema pode ser resolvido com a ajuda de métodos modernos de visão computacional treinados. Por exemplo, a rede YOLO retorna a caixa delimitadora do objeto desejado - e é isso que nos interessa. Sim, testamos e lançamos com êxito uma solução baseada em aprendizado profundo - mas como uma segunda iteração (já após o lançamento da ferramenta de localização e o início da operação). Essas soluções são mais resistentes a alterações nos parâmetros dos botões e têm muitas propriedades positivas: por exemplo, em vez de pegar limites e parâmetros com as mãos, você pode simplesmente adicionar exemplos de banners nos quais a rede está errada (Aprendizado Ativo) no conjunto de treinamento. Usar o aprendizado profundo para nossa tarefa tem seus problemas e pontos interessantes. Por exemplo, muitos métodos modernos de visão computacional requerem um grande número de imagens marcadas, mas não tivemos marcação (como em muitos casos reais), e o número total de banners diferentes não excede vários milhares. Portanto, decidimos organizar um pequeno número de imagens e escrever um gerador que criará outros banners semelhantes com base. Nesta direção, existem muitos truques interessantes . Existem muitas outras armadilhas, e a própria tarefa de determinar a posição de um objeto de visão computacional é extensa e tem muitas soluções. Portanto, decidiu-se limitar o campo de visão do artigo, e as decisões baseadas na aprendizagem profunda não foram consideradas.

O código com blocos de notas que implementam os métodos descritos e desenham figuras do artigo pode ser encontrado no repositório ).