Este post clássico detalha as maneiras mais populares de criar e passar por labirintos. O artigo está dividido em quatro partes: classificação, algoritmos de geração, algoritmos para resolver labirintos e outras operações com labirintos.Classificação do labirinto
Os labirintos como um todo (e, portanto, os algoritmos para criá-los) podem ser divididos em sete classificações diferentes: dimensão, hiperdimensão, topologia, mosaico, roteamento, textura e prioridade. O labirinto pode usar um elemento de cada classe em qualquer combinação.
Dimensão: a classe de dimensão determina essencialmente quantas dimensões no espaço o labirinto preenche. Os seguintes tipos estão disponíveis:

Bidimensional : a maioria dos labirintos, tanto em papel quanto em real, tem essa dimensão, ou seja, sempre podemos exibir o plano do labirinto em uma folha de papel e movê-lo sem cruzar outros corredores do labirinto.- Tridimensional : labirinto tridimensional tem vários níveis; nele (pelo menos na versão ortogonal), as passagens podem, além das quatro direções cardeais, descer e subir. Um labirinto 3D é frequentemente visualizado como uma matriz de níveis 2D com escadas para cima e para baixo.
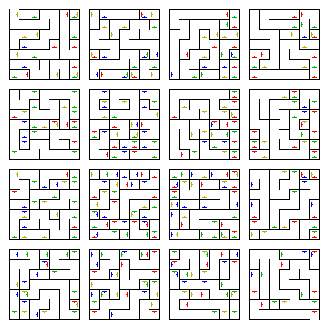
Dimensões mais altas : você pode criar labirintos quadridimensionais e ainda mais multidimensionais. Às vezes, eles são visualizados como labirintos em 3D com "portais" que levam até a quarta dimensão, por exemplo, portais para o "passado" e o "futuro".
Entrelaçamento : labirintos com entrelaçamento - são essencialmente labirintos bidimensionais (ou melhor, 2.5 dimensionais), nos quais, no entanto, as passagens podem se sobrepor. Ao exibir, geralmente é bastante óbvio onde estão os becos sem saída e como uma passagem está acima da outra. Labirintos do mundo real, nos quais existem pontes conectando uma parte do labirinto com outra, são parcialmente entrelaçados.
Hyperdimension: a classificação de acordo com a hyperdimension corresponde à dimensão de um objeto que se move através de um labirinto, e não ao próprio labirinto. Os seguintes tipos estão disponíveis:

Não-hiperlabirintos : quase todos os labirintos, mesmo aqueles criados em alta dimensionalidade ou com regras especiais, geralmente são não-hiperlabirintos. Nelas, trabalhamos com um ponto ou um objeto pequeno, por exemplo, uma bola ou o próprio jogador, que se move de um ponto a outro, e a rota pavimentada forma uma linha. Em cada ponto, há um número de opções facilmente contável.- Hyperlabyrinths: hyperlabyrinths são labirintos nos quais o objeto que está sendo resolvido não é apenas um ponto. Um hiperlabirinto padrão (ou hiperlabirinto de primeira ordem) consiste em uma linha que forma uma superfície ao se mover ao longo de um caminho. O hiperlabirinto pode existir apenas em 3D ou em um meio com uma dimensão maior, e a entrada no hiperlabirinto geralmente não é um ponto, mas uma linha. O Hyperlabyrinth é fundamentalmente diferente, porque é necessário levar em consideração e trabalhar simultaneamente com várias partes da linha, e a qualquer momento existe um número quase infinito de estados e opções para o que pode ser feito com a linha. A linha de solução é infinita ou seus pontos de extremidade estão fora do hiperlabirinto para evitar que a linha seja compactada em um ponto, pois, neste caso, pode ser considerado um não-hiperlabirinto.
- Hiper-hiperlabirinto: os hiperlabirintos podem ter uma dimensão arbitrariamente alta. O hiper-hiper-labirinto (ou hiper-labirinto de segunda ordem) aumenta novamente a dimensão do objeto que está sendo resolvido. Aqui, o objeto a ser resolvido é um plano que, ao se mover pelo caminho, forma uma figura tridimensional. O hiper-hiperlabirinto pode existir apenas em ambientes dimensionais 4D ou superiores.
Topologia: a classe de topologia descreve a geometria do espaço do labirinto no qual ele existe como um todo. Os seguintes tipos estão disponíveis:

Normal : Este é o labirinto padrão no espaço euclidiano.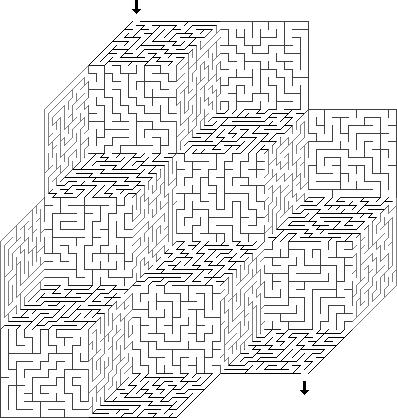
Planair : O termo "planair" descreve qualquer labirinto com uma topologia incomum. Normalmente, isso significa que as bordas do labirinto estão conectadas de uma maneira interessante. Exemplos: labirintos na superfície de um cubo, labirintos na superfície de uma faixa de Mobius e labirintos equivalentes aos de um toro onde os lados esquerdo e direito, superior e inferior estão conectados em pares.
Tecelagem: uma classificação da geometria das células individuais que compõem o labirinto. Tipos existentes:

Ortogonal : Esta é uma grade retangular padrão na qual as células têm passagens que se cruzam em ângulos retos. No contexto do mosaico, eles também podem ser chamados de labirintos gama.
Delta : Os labirintos Delta consistem em triângulos conectados e cada célula pode ter até três passagens conectadas a ela.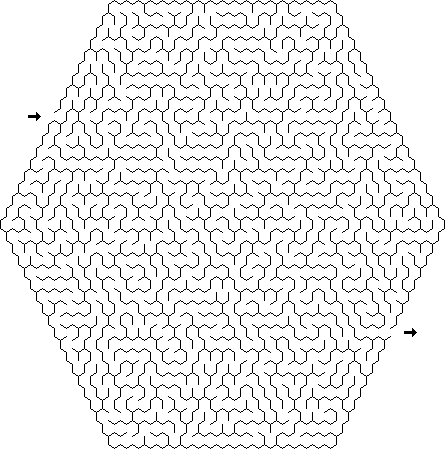
Sigma : Os labirintos Sigma são compostos de hexágonos conectados; cada célula pode ter até seis passagens.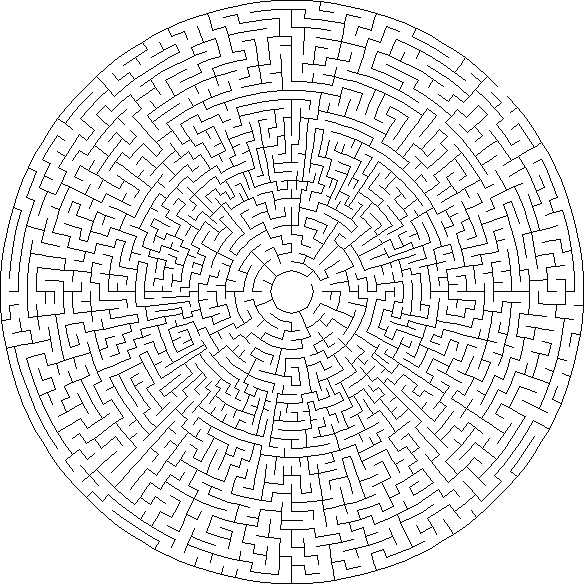
Teta : Os labirintos teta consistem em círculos concêntricos de passagens nas quais o começo ou o fim está no centro e o outro na borda externa. As células geralmente têm quatro caminhos de conexão possíveis, mas pode haver mais devido ao maior número de células nos anéis externos das passagens.
Epsilon : Os labirintos Epsilon consistem em octógonos ou quadrados conectados, cada célula neles pode ter até oito ou quatro passagens.
Zeta : O labirinto zeta está localizado em uma grade retangular; somente além das passagens horizontais e verticais, as passagens diagonais são permitidas em um ângulo de 45 graus.
Ômega : o termo ômega refere-se a quase todos os labirintos com mosaico não ortogonal constante. Os labirintos delta, sigma, teta e ipsilon são desse tipo, como muitos outros esquemas em que você pode pensar, por exemplo, em um labirinto que consiste em pares de triângulos retângulos.
Rachadura : Um labirinto de crack é um labirinto amorfo sem mosaico constante, no qual paredes e passarelas estão localizadas em ângulos aleatórios.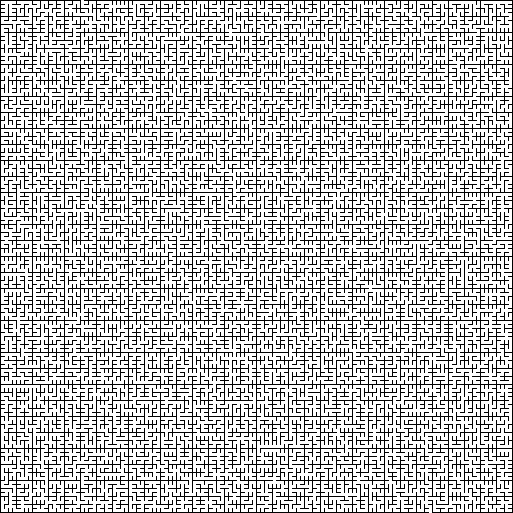
Fractal : Um labirinto fractal é um labirinto composto de labirintos menores. Um labirinto fractal de células aninhadas é um labirinto em cada célula da qual outros labirintos são colocados, e esse processo pode ser repetido várias vezes. Um labirinto fractal infinitamente recursivo é um verdadeiro fractal no qual o conteúdo do labirinto se replica, criando um labirinto essencialmente infinitamente grande.
Roteamento: a classificação por roteamento é provavelmente o aspecto mais interessante na geração de labirintos. From está associado a tipos de passes dentro da geometria definida nas categorias descritas acima.

Ideal : “ideal” é um labirinto sem loops ou circuitos fechados e sem áreas inacessíveis. É também chamado de labirinto simplesmente conectado. De cada ponto, há exatamente um caminho para qualquer outro ponto. Labirinto tem apenas uma solução. Do ponto de vista da programação, esse labirinto pode ser descrito como uma árvore, um conjunto de células ou vértices de conexão.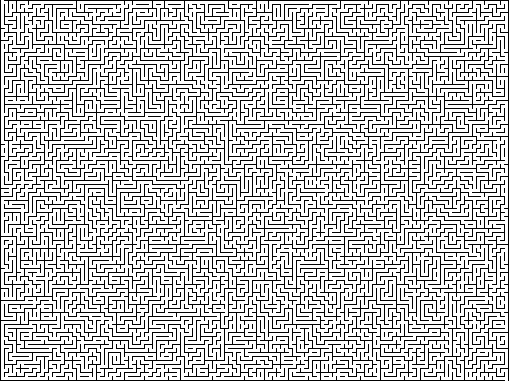
Trançado : Trançado significa que não há becos sem saída no labirinto. É também chamado de labirinto de labirintos puramente multiplicado. Nesse labirinto, são usadas passagens que são fechadas e retornam uma à outra (daí o nome “vime”), fazendo com que passem mais tempo andando em círculos, em vez de chegar a becos sem saída. Um labirinto tecido de qualidade pode ser muito mais complicado que um labirinto ideal do mesmo tamanho.
Via única (Unicursal) : rota única significa um labirinto sem garfos. O labirinto de mão única contém uma passagem longa e sinuosa que muda de direção por todo o labirinto. Não é muito complicado, apenas se você não voltar acidentalmente até a metade e não voltar ao início.
Esparso: um labirinto esparso não passa por cada célula, ou seja, alguns deles não são criados. Isso implica a presença de áreas inacessíveis, ou seja, de certa forma, é o oposto do labirinto de vime. Um conceito semelhante pode ser aplicado ao adicionar paredes, para que você possa obter um labirinto irregular com corredores e salas amplas.- Parcialmente vime: O labirinto parcialmente vime é um labirinto misto que possui loops e becos sem saída. A palavra "vime" pode ser usada para avaliação quantitativa, ou seja, um "labirinto com tecelagem forte" é um labirinto com muitas voltas ou paredes removidas, e há apenas alguns no "labirinto com tecelagem fraca".
Textura: a classificação da
textura descreve o estilo de passes com roteamento e geometria diferentes. A textura não é apenas parâmetros que podem ser ativados ou desativados. Aqui estão alguns exemplos de variáveis:

Viés : em um labirinto com passagens deslocadas, as passagens retas tendem a ir mais em uma direção do que em outras. Por exemplo, em um labirinto com alto deslocamento horizontal, teremos longas passagens da esquerda para a direita e apenas pequenas passagens de cima para baixo conectando-as. Esse labirinto é geralmente mais difícil de passar "através das fibras".
Sobrecarga : a métrica Sobrecarga determina quanto tempo os corredores levarão antes que os turnos forçados apareçam. Em um labirinto com um vão baixo, não haverá passagens retas com mais de três ou quatro células e parecerá muito aleatório. Em um labirinto com um vão alto, o labirinto terá uma grande porcentagem de passes longos, o que fará com que pareça um microchip.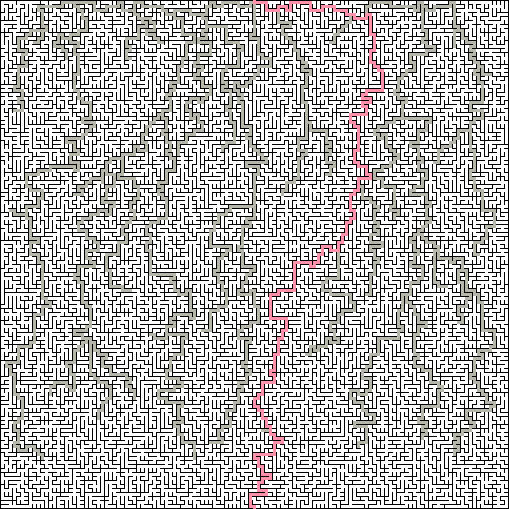
Elitismo: o indicador de “elite” do labirinto determina o comprimento da solução em relação ao tamanho do labirinto. Os labirintos de elite geralmente têm uma solução curta e direta, enquanto nos labirintos que não são de elite, a solução passa por grande parte da área do labirinto. Um labirinto de elite de alta qualidade pode ser muito mais complicado que um labirinto que não é de elite.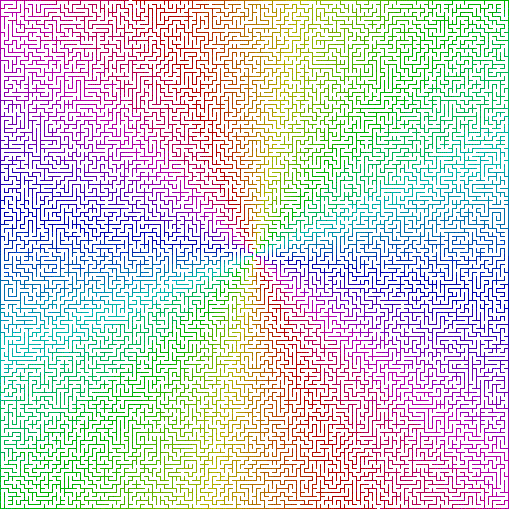
Simetria : um labirinto simétrico possui passagens simétricas, por exemplo, na simetria de rotação em relação ao centro ou refletida ao longo dos eixos horizontal ou vertical. O labirinto pode ser parcial ou completamente simétrico e pode repetir o padrão várias vezes.
Homogeneidade: um algoritmo homogêneo gera todos os labirintos possíveis com igual probabilidade. Um labirinto pode ser chamado com uma textura homogênea se parecer com um labirinto típico gerado por um algoritmo homogêneo. Teoricamente, um algoritmo heterogêneo também pode gerar todos os labirintos possíveis em qualquer espaço, mas não com igual probabilidade. A heterogeneidade pode ir ainda mais longe - pode haver labirintos que o algoritmo nunca gerará.- Fluxo do rio: A característica "fluxo" significa que, ao criar um labirinto, o algoritmo procurará e limpará as células (ou paredes) vizinhas à atual, ou seja, fluirá (daí o termo "fluidez") para as partes ainda não criadas do labirinto, como a água. Em um labirinto ideal com uma taxa de fluxo mais baixa, geralmente haverá muitos becos sem saída curtos, e em um labirinto mais "fluido" haverá menos becos sem saída, mas serão mais longos.
Prioridade: esta classificação mostra que os processos de criação de labirintos podem ser divididos em dois tipos principais: adição de paredes e passagens de entalhe. Geralmente, ao gerar isso, tudo se resume apenas à diferença nos algoritmos, e não às diferenças visíveis nos labirintos, mas ainda é útil levar isso em consideração. O mesmo labirinto é frequentemente gerado de ambos os modos:
- Adicionando paredes: os algoritmos para os quais as paredes são prioritárias começam com uma área vazia (ou borda externa), adicionando paredes no processo. No mundo real, labirintos reais compostos por sebes, tetos ou paredes de madeira estão definitivamente adicionando paredes.
- Corredores de corte: os algoritmos cuja prioridade são corredores começam com um bloco sólido e cortam passagens nele no processo. No mundo real, esses labirintos são túneis de minas ou labirintos dentro de canos.

Predefinição: é claro, os labirintos podem cortar passagens e adicionar paredes simultaneamente; alguns algoritmos de computador fazem isso. Um modelo de labirinto é uma imagem gráfica que não é um labirinto, que no menor número de etapas se transforma em um labirinto real, mas ainda mantém a textura do modelo gráfico original. Estilos complexos de labirinto, como espirais que se cruzam, são mais fáceis de implementar como padrões em um computador do que tentar criar o labirinto certo, preservando seu estilo.
Outro: o acima não é de forma alguma uma lista exaustiva de todas as classes ou elementos possíveis dentro de cada classe. Estes são apenas os tipos de labirintos que eu mesmo criei. Observe que quase todo tipo de labirinto, incluindo labirintos com regras especiais, pode ser expresso como um gráfico direcionado no qual haverá um número finito de estados e um número finito de opções em cada estado, e isso é chamado de
equivalência dos labirintos . Aqui estão algumas outras classificações e tipos de labirintos:

Orientação : em certas passagens, você só pode se mover em uma direção. Do ponto de vista da programação, esse labirinto será descrito por um gráfico direcionado, em contraste com um gráfico não direcionado que descreve todos os outros tipos.
Segmentação : o labirinto pode ter diferentes partes correspondentes a diferentes classes.
Labirintos de comprimento infinito: podemos criar um labirinto infinitamente longo (um número finito de colunas e qualquer número de linhas), mas ao mesmo tempo armazenar apenas uma parte do labirinto na memória, "rolando" de uma extremidade à outra e destruindo as linhas anteriores ao criar a próxima. Um exemplo é uma versão modificada do algoritmo Hunt and Kill. Pode-se imaginar um labirinto potencialmente interminável na forma de um filme longo composto por quadros individuais. Apenas dois quadros consecutivos são armazenados na memória por vez. Vamos executar o algoritmo Hunt and Kill, embora ele crie um viés que é propenso ao quadro superior, então ele termina primeiro. Após a conclusão, o quadro não é mais necessário, você pode imprimi-lo ou fazer outra coisa com ele. Seja como for, descarte-o, torne o quadro inferior parcialmente criado um novo quadro superior e limpe o novo quadro inferior. Repita o processo até decidirmos parar e aguarde até que Hunt And Kill complete os dois quadros. A única limitação é que o labirinto nunca terá um caminho que se ramifica em direção à entrada por um comprimento de mais de dois quadros. A maneira mais fácil de criar um labirinto sem fim é o algoritmo Eller ou Sidewinder, porque eles já criam labirintos uma linha de cada vez, para que você possa deixá-los adicionar infinitamente linhas ao labirinto.
Labirintos fractais virtuais : virtual é um labirinto no qual o labirinto inteiro não é armazenado na memória ao mesmo tempo. Por exemplo, ele pode armazenar apenas parte das passagens de 100x100 próximas à sua localização em uma simulação em que você caminha por um grande labirinto. A extensão de labirintos fractal aninhados pode ser usada para criar enormes labirintos virtuais, por exemplo, um bilhão por bilhão de passes. Se construíssemos uma cópia real do labirinto de um bilhão por bilhão de passes (com uma distância de seis pés entre as passagens), então ela preencheria a superfície da Terra mais de 6.000 vezes! Considere um labirinto de 10 9 a 10 9 passes, ou um labirinto fechado com apenas 9 níveis. Se quisermos ter pelo menos uma parte de 100x100 em torno de nós, basta criar um nível labirinto inferior de 100x100 passes e sete labirintos 10x10 nos quais está incorporado, a fim de saber exatamente onde as paredes estão na parte 100x100. (Na verdade, é melhor ter quatro partes adjacentes de tamanho 100x100, formando um quadrado, caso você esteja próximo da borda ou canto da peça, mas o mesmo conceito se aplica aqui.) Para garantir que o labirinto seja constante e inalterado ao movê-lo, temos uma fórmula: definindo um número de semente aleatória para cada coordenada em cada nível de aninhamento. Os labirintos de fractal virtual são semelhantes ao fractal de Mandelbrot, nas imagens em que ele existe virtualmente, e precisamos visitar uma determinada coordenada com uma ampliação bastante alta. para que apareça.
Algoritmos de labirinto
Aqui está uma lista de algoritmos generalizados para criar as várias classes de labirintos descritas acima:

Ideal : para criar um labirinto ideal padrão, geralmente é necessário “cultivá-lo”, garantindo a ausência de loops e áreas isoladas. Começamos a partir da parede externa e adicionamos aleatoriamente um fragmento da parede que a toca. Continuamos adicionando aleatoriamente segmentos de parede ao labirinto, mas certifique-se de que cada novo segmento toque em uma extremidade da parede existente e sua outra extremidade esteja na parte ainda não criada do labirinto. Se você adicionar um segmento de parede, cujas duas extremidades são separadas do resto do labirinto, isso criará uma parede não conectada com um laço em volta e, se você adicionar um segmento, cujas extremidades tocam o labirinto, isso criará uma área inacessível. Este é um método de adicionar paredes; é quase análogo ao recorte de passagens, em que partes das passagens são cortadas, de modo que apenas uma extremidade toque a passagem existente.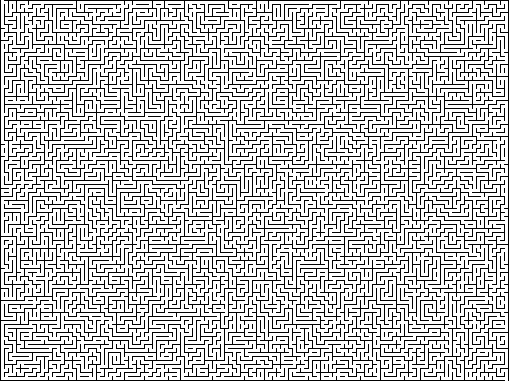
: , , . : (1) , (2) , , -«», (3) , , , (4) , , (3) , , .
: — , , , , . U- , , , , . . , : , , , . , . , .
: , . , , . - , , , , .- 3D : , , , . - .

: , , . ( ): , , , . , . , ; , . , , .
Crack : Crack- , , . , , , «» . , , . , - . , , ; . , .
: «» , , . , - : (1) , . (2) , , , , , (.. ). (3) , , . , .
: — 3D-, -, , . 3D- , , . , , . , . , ( ), , , .
Planair : Planair- , . — . , .
: , , , -, , , , . , . , , , , , .
Existem muitas maneiras de criar labirintos perfeitos, e cada uma delas tem suas próprias características. Abaixo está uma lista de algoritmos específicos. Todos eles descrevem a criação de um labirinto cortando passagens, no entanto, a menos que seja indicado o contrário, cada um também pode ser implementado adicionando paredes: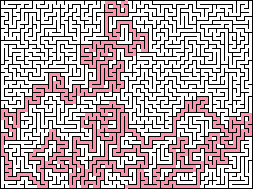
Backtracker recursivo : - recursive backtracker, , . , , . , , . , . , . , , , . , . Recursive backtracking , , , .
: , . , «» , , . , , ( ). , . , , . , - , , . , , . , . , - (union-find algorithm): , . . , - .
Algoritmo de Prim (verdadeiro) : esse algoritmo cria uma árvore de abrangência mínima processando pesos de borda aleatoriamente exclusivos. A quantidade de memória necessária é proporcional ao tamanho do labirinto. Começamos a partir de qualquer vértice (o labirinto acabado será o mesmo, não importa de onde partimos). Selecionamos a aresta da passagem com o menor peso que conecta o labirinto a um ponto que ainda não está nele e depois a anexamos ao labirinto. O labirinto é concluído quando as bordas em questão não são mais deixadas. Para selecionar com eficiência a próxima borda, você precisa de uma fila de prioridade (geralmente implementada usando um heap) que armazena todas as bordas da borda. No entanto, esse algoritmo é bastante lento porque leva tempo de log (n) para selecionar itens do heap. Portanto, é melhor preferir o algoritmo Kraskal, que também cria uma árvore de abrangência mínima, porque é mais rápido e cria labirintos com uma estrutura idêntica. De fato, com a mesma semente aleatória, os algoritmos Prima e Kraskal podem criar os mesmos labirintos.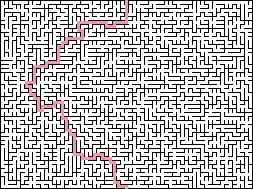
Algoritmo de Prim (simplificado) : o algoritmo deste Prim cria uma árvore de abrangência mínima. É simplificado de forma que todos os pesos das arestas sejam os mesmos. Requer uma capacidade de memória proporcional ao tamanho do labirinto. Começamos a partir de um pico aleatório. Selecionamos aleatoriamente a aresta da passagem que conecta o labirinto com um ponto que ainda não está nele e, em seguida, o anexamos ao labirinto. O labirinto é concluído quando as bordas em questão não são mais deixadas. Como as arestas não têm peso e não são ordenadas, elas podem ser armazenadas como uma lista simples, ou seja, a seleção de elementos da lista será muito rápida e levará tempo constante. Portanto, é muito mais rápido que o verdadeiro algoritmo Prim, com pesos de borda aleatórios. A textura de labirinto criada terá uma taxa de fluxo mais baixa e uma solução mais simples do que o método Prim verdadeiro, porque se espalha do ponto de partida uniformemente, como xarope derramado, e não ignora fragmentos de costelas com um peso maior, que serão levados em consideração posteriormente.
Algoritmo do Prim (modificado) : o algoritmo do Prim cria uma árvore de abrangência mínima, modificada para que todos os pesos das arestas sejam os mesmos. No entanto, é implementado de tal maneira que, em vez de bordas, ele olha para as células. A quantidade de memória é proporcional ao tamanho do labirinto. No processo de criação, cada célula pode ter um dos três tipos: (1) “interno”: a célula faz parte do labirinto e já está cortada nele; (2) “limite”: a célula não faz parte do labirinto e ainda não foi cortada nele, mas está localizada próximo à célula que já é "interna" e (3) "externa": a célula ainda não faz parte do labirinto e nenhum de seus vizinhos também é a célula "interna". Começamos escolhendo uma célula, a tornamos "interna" e, para todos os seus vizinhos, definimos o tipo como "limite". Selecionamos aleatoriamente a célula “limite” e cortamos uma passagem de uma das células “internas” vizinhas para dentro dela. Mudamos o estado dessa célula "limite" para "interno" e alteramos o tipo de todos os seus vizinhos de "externo" para "fronteira". O labirinto é concluído quando não há mais células "de fronteira" (isto é, não existem células "externas", o que significa que todos se tornaram "internos"). Esse algoritmo cria labirintos com um índice de rendimento muito baixo, possui muitos impasses curtos e uma solução bastante direta. O labirinto resultante é muito semelhante ao resultado do algoritmo Prima simplificado, com uma pequena diferença: os vazios na árvore de abrangência são preenchidos apenas se uma célula de fronteira for selecionada aleatoriamente, em contraste com a probabilidade tripla de encher essa célula através de uma das células de fronteira que o levam. Além disso, o algoritmo é muito rápido, mais rápido que o algoritmo Prim simplificado, porque não precisa compilar e processar a lista de arestas.
Algoritmo Aldous-Broder : o que é interessante nesse algoritmo é que ele é homogêneo, ou seja, cria com igual probabilidade todos os labirintos possíveis de um determinado tamanho. Além disso, ele não requer memória adicional ou uma pilha. Selecionamos um ponto e movemos aleatoriamente para uma célula vizinha. Se entrarmos em uma célula sem cortes, recorte a passagem da célula anterior para ela. Continuamos a avançar para células vizinhas até cortar as passagens para todas as células. Esse algoritmo cria labirintos com uma vazão baixa, apenas um pouco maior que o algoritmo de Kraskal. (Isso significa que, para uma determinada troca, há mais labirintos com um índice de rendimento baixo do que com um alto, porque o labirinto com uma probabilidade média é igualmente baixa.) O ruim desse algoritmo é que ele é muito lento porque não realiza uma pesquisa intelectual pelo último. células, isto é, de fato, não tem garantias de conclusão. No entanto, devido à sua simplicidade, ele pode passar rapidamente por muitas células, sendo concluído mais rapidamente do que você imagina. Em média, leva sete vezes mais tempo para ser concluído do que os algoritmos padrão, embora em casos ruins possa demorar muito mais se o gerador de números aleatórios evitar constantemente as últimas células. Ele pode ser implementado como adição de paredes, se a parede da borda for considerada um único vértice, ou seja, por exemplo, se o movimento nos mover para a parede da borda, nos teletransportamos para um ponto aleatório ao longo da borda e só então continuamos a se mover. No caso de adicionar paredes, funciona quase duas vezes mais rápido, porque o teletransporte ao longo da parede da fronteira permite um acesso mais rápido às partes mais distantes do labirinto.
Algoritmo de Wilson : esta é uma versão aprimorada do algoritmo Aldous-Broder, cria labirintos com exatamente a mesma textura (os algoritmos são homogêneos, ou seja, todos os labirintos possíveis são gerados com igual probabilidade), mas o algoritmo de Wilson é muito mais rápido. Leva memória até o tamanho do labirinto. Começamos com uma célula de labirinto inicial selecionada aleatoriamente. Selecionamos uma célula aleatória que ainda não faz parte do labirinto e fazemos uma caminhada aleatória até encontrarmos uma célula que já pertence ao labirinto. Assim que topamos com a parte já criada do labirinto, retornamos à célula aleatória selecionada e cortamos todo o caminho feito adicionando essas células ao labirinto. Mais especificamente, quando retornamos ao longo do caminho, cortamos cada célula na direção em que a caminhada aleatória ocorreu na última vez que saímos da célula. Isso evita o aparecimento de loops ao longo do caminho de retorno, de modo que uma passagem longa se junte ao labirinto. O labirinto é concluído quando todas as células estão conectadas a ele. O algoritmo tem os mesmos problemas de velocidade que Aldous-Broder, porque pode levar muito tempo para encontrar o primeiro caminho aleatório para a célula inicial, mas depois de colocar vários caminhos, o resto do labirinto é cortado rapidamente. Em média, ele roda cinco vezes mais rápido que o Aldous-Broder e menos de duas vezes mais lento que os melhores algoritmos. Vale a pena considerar que, no caso de adicionar paredes, funciona duas vezes mais rápido, porque toda a parede da borda é inicialmente parte do labirinto, de modo que as primeiras paredes se juntam muito mais rapidamente.
Algoritmo de busca e eliminação : esse algoritmo é conveniente porque não requer memória ou pilha adicional e, portanto, é adequado para criar grandes labirintos ou labirintos em computadores fracos devido à impossibilidade de ficar sem memória. Como não possui regras que precisam ser seguidas constantemente, também é mais fácil modificar e criar labirintos com diferentes texturas. É quase semelhante a um backtracker recursivo, mas não há célula não criada perto da posição atual. Entramos no modo "caça" e examinamos sistematicamente o labirinto até encontrarmos uma célula não criada ao lado da célula já cortada. Nesta fase, novamente começamos a cortar neste novo local. O labirinto é concluído quando no modo "caça" todas as células são digitalizadas. Esse algoritmo tende a criar labirintos com uma taxa de fluxo alta, mas não tão alta quanto o backtracker recursivo. Você pode forçá-lo a gerar labirintos com uma taxa de fluxo mais baixa, entrando com mais frequência no modo "caça". Ele corre mais devagar devido ao tempo gasto caçando as últimas células, mas não muito mais lento que o algoritmo de Kraskal. Pode ser implementado de acordo com o princípio de adicionar paredes, se você ocasionalmente se teletransportar aleatoriamente para evitar os problemas inerentes a um backtracker recursivo.
Algoritmo crescente
tree (algoritmo da árvore em crescimento) : este é um algoritmo generalizado que pode criar labirintos com diferentes texturas. A memória necessária pode atingir o tamanho do labirinto. Cada vez que uma célula é cortada, a adicionamos à lista. Selecione uma célula da lista e recorte a passagem para a célula não criada próxima a ela. Se não houver células não criadas próximas à atual, exclua a célula atual da lista. O labirinto é concluído quando não há mais nada na lista. O interessante do algoritmo é que, dependendo de como você seleciona uma célula da lista, é possível criar muitas texturas diferentes. Por exemplo, se você sempre selecionar a última célula adicionada, esse algoritmo se tornará um backtracker recursivo. Se você sempre selecionar células aleatoriamente, ele se comportará de maneira semelhante, mas não idêntica ao algoritmo Prim. Se você sempre selecionar as células mais antigas adicionadas à lista, criaremos um labirinto com o menor índice de rendimento possível, ainda mais baixo que o do algoritmo Prim. Se você costuma escolher a última célula, mas ocasionalmente escolhe uma célula aleatória, o labirinto terá uma taxa de fluxo alta, mas uma solução curta e direta. Se uma das células mais recentes for selecionada aleatoriamente, o labirinto terá uma taxa de fluxo baixa, mas uma solução longa e sinuosa.
Algoritmo crescente da floresta : este é um algoritmo mais generalizado que combina tipos com base em árvores e conjuntos. É uma extensão do algoritmo de crescimento de árvore, que inclui essencialmente várias instâncias que se expandem simultaneamente. Começamos com todas as células classificadas aleatoriamente em uma lista de "novo"; além disso, cada célula tem seu próprio conjunto, como no início do algoritmo de Kruskal. Primeiro, selecione uma ou mais células movendo-as da lista de "novo" para a lista de "ativo". Selecione uma célula da lista "ativa" e recorte a passagem para a próxima célula não criada da lista "nova", adicionando uma nova célula à lista de "ativa" e combinando os conjuntos de duas células. Se for feita uma tentativa de cortar a parte existente do labirinto, ative-a se as células estiverem em conjuntos diferentes e combine as células, como é feito no algoritmo de Kraskal. Se não houver células “novas” próximas à célula atual, mova a célula atual para a lista de células “concluídas”. O labirinto é concluído quando a lista de "ativo" fica vazia. No final, combinamos todos os conjuntos restantes, como no algoritmo de Kruskal. Periodicamente, você pode criar novas árvores movendo uma ou mais células da lista de "novo" para a lista de "ativo", como foi feito no início. Ao controlar o número de árvores originais e os compartilhamentos das árvores recém-criadas, você pode gerar muitas texturas exclusivas que combinam com os parâmetros já flexíveis do algoritmo de crescimento de árvores.
Algoritmo de Eller : esse é um algoritmo especial, porque não é apenas mais rápido que todos os outros, mas também não possui viés ou deficiências óbvias; além disso, quando é criada, a memória é usada com mais eficiência. Nem exige que todo o labirinto esteja na memória, ele usa um volume proporcional ao tamanho da linha. Ele cria um labirinto linha por linha. Após a geração da sequência, o algoritmo não leva mais em consideração. Cada célula em uma linha está contida em um conjunto; duas células pertencem ao mesmo conjunto se houver um caminho entre elas ao longo do labirinto já criado. Esta informação permite cortar passagens na linha atual sem criar loops ou áreas isoladas. De fato, é bastante semelhante ao algoritmo de Kraskal, apenas aqui é formado uma linha de cada vez, enquanto Kraskal olha através de todo o labirinto. A criação de uma linha consiste em duas partes: conecte aleatoriamente as células adjacentes na linha, ou seja, recortamos passagens horizontais e, em seguida, conectamos aleatoriamente as células entre a corrente e a próxima linha, ou seja, cortar passagens verticais. Ao cortar passagens horizontais, não conectamos células que já estão no mesmo conjunto (porque um loop será criado de outra forma) e, ao cortar passagens verticais, devemos conectar uma célula se tiver um tamanho de unidade (porque, se você a deixar, criará uma área isolada). Ao cortar passagens horizontais, conectamos células se elas estiverem no mesmo conjunto (porque agora existe um caminho entre elas) e, ao cortar passagens verticais quando não nos conectamos à célula, colocamos em um conjunto separado (porque agora está separado do resto do labirinto ) A criação começa com o fato de que antes de conectar as células na primeira linha, cada célula tem seu próprio conjunto. A criação é concluída após as células serem conectadas na última linha. Existe uma regra especial de conclusão: no momento da conclusão, cada célula deve estar no mesmo conjunto para evitar áreas isoladas. (A última linha é criada combinando cada um dos pares de células vizinhas que ainda não estão no mesmo conjunto.) É melhor implementar o conjunto usando uma lista cíclica de células duplamente vinculada (que pode ser apenas uma matriz que liga células a pares de células nos dois lados do mesmo conjunto), permitindo realizar a inserção, exclusão e verificação da presença de células vizinhas em um conjunto por um tempo constante. O problema com esse algoritmo é o desequilíbrio no processamento das diferentes bordas do labirinto; Para evitar manchas nas texturas, é necessário conectar e pular as células conectadas nas proporções corretas.
Divisão recursiva: esse algoritmo é um pouco semelhante ao retorno recursivo, porque ambos usam pilhas, só que funciona não com corredores, mas com paredes. Começamos criando uma parede horizontal ou vertical aleatória que cruza uma área acessível em uma linha ou coluna aleatória e colocamos aleatoriamente espaços vazios ao longo dela. Em seguida, repetimos recursivamente o processo para as duas sub-regiões geradas pela parede divisória. Para obter melhores resultados, é necessário adicionar um desvio na escolha de horizontal ou vertical com base nas proporções da área, por exemplo, uma área cuja largura seja duas vezes a altura deve ser mais frequentemente dividida por paredes verticais. Este é o algoritmo mais rápido, sem desvios de direção, e muitas vezes pode até competir com labirintos baseados em árvores binárias, porque cria várias células ao mesmo tempo, embora tenha uma desvantagem óbvia na forma de longas paredes que cruzam o interior do labirinto. Esse algoritmo é uma espécie de labirinto fractal embutido, mas em vez de criar constantemente labirintos de células de tamanho fixo com labirintos do mesmo tamanho dentro de cada célula, divide aleatoriamente uma determinada área em um labirinto de tamanho aleatório: 1x2 ou 2x1. A divisão recursiva não pode ser usada para cortar passagens, porque isso leva à criação de uma solução óbvia que segue ao longo da borda externa ou cruza diretamente o interior.
Labirintos baseados em árvores binárias : na verdade, esses são os algoritmos mais simples e rápidos possíveis, no entanto, os labirintos criados têm uma textura com um viés muito alto. Para cada célula, cortamos uma passagem para cima ou para a esquerda, mas nunca nas duas direções. Na versão com adição de paredes, um segmento de parede é adicionado para cada vértice que desce ou desce à direita, mas não nas duas direções. Cada célula é independente de todas as outras células, porque não precisamos verificar o estado de outras células ao criá-lo. Portanto, este é um algoritmo real para gerar labirintos sem memória, não limitado pelo tamanho dos labirintos criados. De fato, essa é uma árvore binária, se considerarmos o canto superior esquerdo como uma raiz, e cada nó ou célula possui um nó pai exclusivo, que é uma célula no topo ou à esquerda dele. Os labirintos baseados em árvores binárias são diferentes dos labirintos ideais padrão, porque mais da metade dos tipos de células não podem existir neles. Por exemplo, nunca haverá interseções nelas e todos os becos sem saída têm passagens que vão para cima ou para a esquerda e nunca para baixo ou para a direita. Os labirintos tendem a ter passagens na diagonal do canto superior esquerdo para o canto inferior direito, e é muito mais fácil mover-se do canto inferior direito para o canto superior esquerdo. Você sempre pode se mover para cima ou para a esquerda, mas nunca simultaneamente nas duas direções, para poder sempre se mover deterministicamente na diagonal para cima e para a esquerda, sem encontrar barreiras. Você terá a oportunidade de escolher e cair em becos sem saída, movendo-se para baixo e para a direita. , , , .
Sidewinder: , . : , , . , , , , , . , ( , ). , sidewinder . , sidewinder . , sidewinder , , . sidewinder , « ». , sidewinder — , , , , . sidewinder , , , .
| % | | | ? | ? | | | % |
| 0 0 | | | | | N^2 | 379 | 100.0 |
| Recursive Backtracker | 10 | | | | | N^2 | 27 | 19.0 |
| Hunt and Kill | 11 (21) | | | | | 0 0 | 100 (143) | 9.5 (3.9) |
| 23 | | | | | N* | 10 | 7.2 |
| 25 | | | | | 0* | 10 | 2.0 |
| Sidewinder | 27 | | | | | 0* | 12 | 2.6 |
| 28. | | | | | N* | 20 | 4.2 (3.2) |
| 29 | | | | | N^2 | 48 (25) | 4.5 |
| - | 29 | | | | | 0 0 | 279 (208) | 4.5 |
| 30 | | | | | N^2 | 33 | 4.1 |
| () | 30 | | | | | N^2 | 160 | 4.1 |
| () | 32. | | | | | N^2 | 59 | 2.3 |
| () | 36 (31) | | | | | N^2 | 30 | 2.3 |
| 49 (39) | | | | | N^2 | 48 | 11.0 |
| 49 (39) | | | | | N^2 | 76 | 11.0 |
Esta tabela resume as características dos algoritmos para criar labirintos ideais descritos acima. Para comparação, foi adicionado um algoritmo de labirinto de rota única (teoricamente, os labirintos de rota única são ideais). Explicação da coluna:- : , , , 2D-. . , , , . 10% ( ) 49% ( ). Recursive Backtracker 1%. 66%: .
- : : , , . , , , , . , , .
- : , . . , , . Recursive Backtracker , , , . , , . , Hunt and Kill , , .
- : , . , . Sidewinder , . , . Hunt and Kill , , , .
- : . «» , . «» , , . «» , , . , .
- : , . , , (N), (N^2). , ( ). , , . Sidewinder , . , .
- : , , , . , ( 10), . 100x100 Daedalus. , , , .
- : , , . , 100x100 . . «» . , . , . , , , .
Existem muitas maneiras de resolver labirintos, e cada um deles tem suas próprias características. Aqui está uma lista de algoritmos específicos:
Seguindo ao longo das paredes (seguidor de parede) : . («»), . ( ). , ( ) . , . , , . , , , . 3D- , 3D- 2D-, .. , -, -, .
: , «» , . 2D- , , .. . , , . . , , . , , . , , . , , — -1, — 1. , , .. 360 , «». , «», , , , , . , , . , — , .
: (Chain algorithm) , ( ) . , , . , . , , . , . ( ) , . . , , . «» , . , , , . , . , .
Recursive backtracker: , . , . : ( ), «», , , «», , . , , «»; «» . (backtracking) , , . , . , , .
(Trémaux's algorithm): . recursive backtracker : , . , . , , . , , , . ( , .) , (.. ), , , , (.. , ). , , , , , . , . , , .
(Dead end filler) : . , . , , . , . , , . , , .
Cul-de-sac filler : , , . dead end filler, , . ( — , , ) , . dead end filler. , , , , . , , , dead end filler.
Blind alley filler : , , . , . — , , . , , cul-de-sac filler, . . , , , , . , , , ( ). , , . , cul-de-sac filler - , collision solver , - .
Blind alley sealer : blind alley filler , , . . . , , blind alley filler, . . , , , , . , , . , . , , . , , .
(Shortest path finder): , , . , , . collision solver, , , «» , ( ), «» , , . «», , . , - , . , , , A* , .
(Shortest paths finder) : , . , , , , , , , - , . , , , «» , , , . , , , , . , .- Collision solver: "amoeba" solver. . , . «» , ( ). « » ( ), , . «», , , , . ( , «», . , , , .) , shortest paths finder, ( ) ( ).
- Rato aleatório: para contraste, darei um método ineficaz para resolver um labirinto, que consiste essencialmente em movimento aleatório, ou seja, movendo-se em uma direção e seguindo esta passagem com todas as curvas até chegarmos ao próximo garfo. Não fazemos curvas de 180 graus, se você puder ficar sem elas. Isso simula o comportamento de uma pessoa que vagueia acidentalmente por um labirinto e não se lembra de onde já estava. O algoritmo é lento e não garante a conclusão ou solução do labirinto e, após chegar ao fim, será igualmente difícil retornar ao início, mas é simples e não requer memória adicional para implementação.
| Algoritmo | Soluções | Garantia? | Prioridade | Disponível para humanos? | Independente dos corredores? | Não é necessária memória? | Rápido? |
| Rato aleatório | 1 | Não | Você é | Por dentro / por cima | Não | Sim | Não |
| Seguidor de parede | 1 | Não | Você é | Por dentro / por cima | Sim | Sim | Sim |
| Algoritmo de Penhor | 1 | Não | Você é | Por dentro / por cima | Sim | Sim | Sim |
| Algoritmo de circuito | 1 | Sim | Você + | Não | Sim | Não | Sim |
| Backtracker recursivo | 1 | Sim | Você é | Não | Sim | Não | Sim |
| Algoritmo de Tremo | 1 | Sim | Você é | Por dentro / por cima | Não | Não | Sim |
| Massa sem saída | Tudo + | Não | Labirinto | Over | Não | Sim | Sim |
| Enchimento de fundo de saco | Tudo + | Não | Labirinto | Over | Não | Sim | Sim |
| Aferidor de becos sem saída | Tudo + | Sim | Labirinto | Não | Não | Não | Sim |
| Enchimento de beco sem saída | Todos | Sim | Labirinto | Over | Não | Sim | Não |
| Solucionador de colisão | Todos os mais curtos | Sim | Você + | Não | Não | Não | Sim |
| Pesquise os caminhos mais curtos | Todos os mais curtos | Sim | Você + | Não | Sim | Não | Sim |
| Procure o caminho mais curto | 1 mais curto | Sim | Você + | Não | Sim | Não | Sim |
Esta tabela lista brevemente as características dos algoritmos de resolução de labirinto descritos acima. De acordo com esses critérios, é possível classificar e avaliar algoritmos para a resolução de labirintos. Explicações da coluna:
- Soluções: descreve as soluções encontradas pelo algoritmo e as ações do algoritmo, se houver várias. O algoritmo pode escolher uma solução ou deixar várias. Além disso, as soluções podem ser qualquer caminho ou o caminho mais curto. O preenchimento sem saída e o preenchimento de um beco sem saída (assim como o selador de becos sem saída ao processar suas áreas inacessíveis) deixam todas as soluções; no entanto, eles também podem deixar passagens que não estão em nenhum dos caminhos da solução, então eu as marquei como "Tudo + "
- Garantia: O algoritmo tem garantia de encontrar pelo menos uma solução? Para mouse aleatório, “não” é indicado, porque sua conclusão não é garantida, e para o seguidor de parede e o algoritmo do Colégio, “não” é indicado, porque eles não serão capazes de encontrar uma solução se o alvo estiver dentro da ilha. "Dead" é indicado para preenchimento sem saída e preenchimento de becos sem saída, porque em labirintos de vime eles podem não encontrar uma solução.
- Prioridade: Existem dois tipos de algoritmos para resolver o labirinto: dar prioridade a "você" (localizado no labirinto) ou dar prioridade ao labirinto. Se a prioridade é dada a você, temos um ponto (“Você” é indicado na tabela) ou muitos pontos (“Você +”) e o algoritmo tenta desenhá-los do início ao fim do labirinto. Se for dada prioridade ao labirinto, examinamos o labirinto como um todo e descartamos passagens inúteis.
- Disponível para o homem: um homem pode usar o algoritmo para resolver o labirinto, no labirinto real ou olhando o mapa de cima. Alguns dos algoritmos que dão prioridade a "você" podem ser implementados como uma pessoa dentro do labirinto (ou acima dele), e alguns que dão prioridade ao labirinto podem ser implementados como uma pessoa, mas apenas acima do labirinto. Outros algoritmos são muito complexos e sua implementação confiável é possível apenas em um computador.
- Passagem independente: o algoritmo pode ser executado em qualquer lugar. Alguns algoritmos exigem que o labirinto tenha passagens óbvias ou, falando na terminologia de gráficos, arestas claras entre vértices individuais ou passagens de um pixel quando implementadas em um computador. O seguidor de Wall, o algoritmo Pledge e o algoritmo de circuito requerem uma parede apenas de um lado. O backtracker recursivo e o localizador de caminhos mais curto direcionam os deles por espaços abertos.
- Não é necessária memória: você precisa de memória adicional ou uma pilha para implementar o algoritmo. Algoritmos eficazes exigem apenas um bitmap do próprio labirinto e não precisam adicionar marcadores ao labirinto no processo de solução.
- Rápido: o processo de decisão é considerado rápido. Os algoritmos mais eficientes são suficientes para examinar cada célula do labirinto apenas uma vez, ou podem pular completamente partes dele. O tempo de execução deve ser proporcional ao tamanho do labirinto, ou O (n ^ 2), onde n é o número de células ao longo de um lado. O mouse aleatório é lento porque sua conclusão não é garantida, e o enchimento de becos sem saída potencialmente resolve o labirinto de cada garfo.
Outras operações com labirintos
Além de criar e resolver labirintos, você pode executar outras operações com eles:

Preenchimento: é uma função “rápida e suja”, mas útil que pode ser implementada com uma única chamada para o procedimento da biblioteca gráfica Fill ou FloodFill. Realizamos o preenchimento de inundação da passagem no início e, se o final não for inundado, o labirinto não terá solução. Nos labirintos, cuja entrada e saída estão nas bordas, realizamos o FloodFill de uma parede e as bordas restantes marcam a solução. Nos labirintos onde estão o início e o fim, executamos o FloodFill da parede delimitadora e, se a parede de saída não tiver sido removida, esse labirinto não poderá ser resolvido seguindo-se as paredes. Muitos métodos de criação de labirintos e outras funções usam o "preenchimento" do labirinto em determinados pontos.
Removedor de isolamento: Troque o labirinto para que ele não tenha partes com passagens que não possam ser alcançadas pelo resto do labirinto. Isso é realizado removendo as paredes que conectam essas partes com o resto do labirinto. Começamos com uma cópia do labirinto, depois preenchemos a passagem perto do início. Examinamos o labirinto (de preferência em ordem aleatória, mas com uma visita a todas as células possíveis) quanto à presença de células não preenchidas adjacentes à célula preenchida. Excluímos o segmento da parede nesse ponto do labirinto original, preenchemos o labirinto nesse novo ponto e repetimos até que todas as peças estejam preenchidas. Esta função é usada para criar labirintos tecidos e estampados.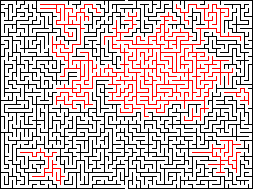
Remoção de alça: mude o labirinto para que não haja laços e paredes não conectados a nada, e cada parte do labirinto pode ser alcançada a partir de qualquer ponto de apenas uma maneira. A implementação dessa função é quase semelhante à remoção de áreas isoladas, apenas percebemos as paredes como passagens e vice-versa. Começamos com uma cópia do labirinto e depois enchemos as paredes externas. Escaneamos o labirinto (de preferência em ordem aleatória, mas com uma visita a todos os possíveis topos das paredes) quanto à presença de paredes não preenchidas próximas às preenchidas. Adicione um segmento de parede conectando as duas partes das paredes ao labirinto original nesse ponto, encha o labirinto nesse novo ponto e repita até que todas as peças estejam preenchidas. Esta função é usada para criar labirintos de modelos e pode ser usada para converter labirintos de vime em ideais, que, no entanto, permanecem semelhantes aos originais.
Procure por gargalos : pesquise no labirinto de passagens ou pontos de interseção pelos quais todas as soluções desse labirinto passam. Para fazer isso, comece a seguir ao longo das paredes com o método da mão esquerda para obter a solução esquerda e comece a seguir ao longo das paredes com o método da mão direita para obter a solução certa. Os lugares em que as duas soluções são comuns são gargalos. No entanto, essa técnica funciona apenas para labirintos, que podem ser resolvidos com sucesso seguindo-se ao longo das paredes. Em outros labirintos, para encontrar gargalos, você precisa encontrar qualquer solução e executar o selador de becos sem saída (isso pode tornar o labirinto insolúvel se perceber a entrada ou a saída dentro do labirinto como um grande beco sem saída). Partes do caminho da solução que passam por passagens fechadas são gargalos.
Implementações de algoritmos
- Daedalus : todos os algoritmos para criação e solução de labirintos descritos acima são implementados no Daedalus, um programa gratuito e disponível para download no Windows. Completo com Daedalus, há um código fonte completo.