Gugology (isto não é um erro de digitação) para programadores

É mais difícil escrever sobre matemática (para que seja interessante) do que sobre física. No entanto, espero que você leia pelo menos os exemplos de programas C loucos.


Monstros podem crescer a partir de coisas completamente inofensivas. Veja, por exemplo, o jogo de substrings. Escrevemos uma sequência de letras aeb e selecionamos substrings do caractere 1 ao caractere 2, de 2 a 4, de três a 6, de n a 2n, até que o comprimento da sequência principal seja suficiente. Nossa tarefa é garantir que nessas subseqüências o menor não entre mais. Eu até escrevi um analisador SQL:

declare @s varchar(max) = 'abbbaaaaaaab' declare @n int=1 declare @sub table (n int, sub varchar(max)) while @n*2<=len(@s) begin insert into @sub select @n,substring(@s,@n,@n+1) set @n=@n+1 end select *,(select max(sub) from @sub I where In>On and charindex(O.sub,I.sub)>0) as FoundMatch from @sub O order by 1 

Aqui está um exemplo de saída:



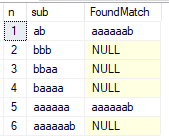
Como você pode ver, as subseqüências 1 e 5 não passaram no teste. Podemos remover o último caractere e a sequência de 11 caracteres resultante 'abbbaaaaaaaa' passará no teste. Acontece que essa é a string mais longa possível no alfabeto de dois caracteres que satisfaz essa condição.

Para um alfabeto de um caractere, o comprimento máximo da string é 3 e, por motivos puramente técnicos. Acontece que o comprimento máximo é finito para um alfabeto de qualquer número de letras. Então nós temos:

$$

$$f (1) = 3$$

$$

$$f (2) = 11$$

$$

$$f (3) = ???$$

Teste sua intuição sobre quanto tempo uma string pode ser criada em um alfabeto de três letras. 100? 1000? De fato, muito mais que Googol e muito mais que GoogolPlekh.

$$

$$f (3)> 2 \ uparrow ^ {7198} 158836$$

E eu tenho que gastar tempo para mostrar a força dos atiradores.

Setas (hiperoperação)

Usamos multiplicação para não escrever muitas operações de adição:

$$

$$2 * 5 = 2 + 2 + 2 + 2 + 2$$

Usamos exponenciação para não escrever muitas multiplicações:

$$

$$2 ^ 3 = 2 * 2 * 2$$

Considerando adição como uma operação de nível 0, multiplicação como 1, exponenciação como 2, podemos introduzir a operação "flecha", por exemplo,

$$

$$3 \ uparrow 3 = 3 ^ {(3 ^ 3)} = 3 ^ {27} = 7'625'597'484'987$$

Observe que os parênteses já são importantes aqui. O próximo nível é a operação com duas setas:

$$

$$3 \ uparrow \ uparrow 3 = 3 \ uparrow (3 \ uparrow 3) = 3 \ uparrow 7625597484987 = 3 ^ {3 ^ {... ^ 3}}$$

A última pirâmide de triplos tem uma altura de 7 bilhões, e esse número já é muito, muito maior que o googol e os googolpleks. Denotamos esse número enorme como Escuridão (era um número tão grande no antigo idioma russo) e tentamos dar mais um passo:

$$

$$3 \ uparrow ^ 3 3 = 3 \ uparrow \ uparrow \ uparrow 3 = 3 \ uparrow \ uparrow (3 \ uparrow \ uparrow 3) = 3 \ uparrow \ uparrow {escuridão} = 3 \ uparrow 3 \ uparrow 3 ... \ uparrow 3$$

(e tantas vezes) ... Já é possível imaginar o tamanho desse número. Observe que, quando há muitas setas, escrevemos um repetidor no topo. Então você pode entender como é ótimo

$$

$$f (3)> 2 \ uparrow ^ {7198} 158836$$

E mais

Usando as setas, apenas o menor número grande é criado, por assim dizer. A taxa de crescimento de funções é medida em uma determinada escala - comparando com funções de crescimento rápido . A primeira função nessa hierarquia corresponde à adição, a segunda à multiplicação, a terceira à flecha, a n-ésima a n-2 (aproximadamente, não exatamente). Mas você pode definir

$$

$$f_w (n) = f_n (n)$$

Essa função para n = 3 é comparável a uma seta, para n = 4 com duas setas e, à medida que o parâmetro n cresce, ultrapassa o crescimento da função com qualquer número estático de setas.

Você pode ir ainda mais longe: $$$f_w, f_ {w + 1}, f_ {w + n}, f_ {w2}, f_ {w ^ 2}, f_ {w ^ w}, f_ {w ^ {w ^ {w}}}, f_ \ epsilon$ Essas funções são indexadas por ordinais ou na literatura russa por números ordinais. A figura com a estrutura dos números ordinais iniciais precede o artigo, mas eles se estendem muito mais e começam mais

Pouco misticismo

A pirâmide interminável de ômega dá uma ordem $$$\ epsilon_0$ . Leia sobre a função cujo crescimento é medido por este ordinal. Acontece que uma função cresce tão rápido que a aritmética formal não pode, em princípio, provar que essa função está definida!

Obviamente, você sabe sobre o teorema de Godel que existem afirmações não prováveis. Mas, como regra, o único exemplo dessa afirmação é a própria construção de Gödel ("eu sou improvável"). O teorema de Goodstein é um bom exemplo dessa afirmação.

Além disso, verifica-se que os ordinais de alguma forma medem o poder das teorias . A 'força' da aritmética formal é $$$\ epsilon_0$ , a teoria simplificada dos conjuntos de Kripke-Plateka tem a força do ordinal de Feferman-Schutte , etc.

Tin - torniquete de matemática - competição em linguagem C

Foi realizada uma competição para gerar grandes números. Não, a programação para uma máquina de Turing ainda é muito cruel, então C foi usado para uma máquina infinita abstrata com sizeof (int) = infinito. Você também pode usar malloc (), e a quantidade de memória, como a pilha, é ilimitada. Somente o tamanho do programa era limitado - o programa tinha que caber em 512 bytes (excluindo espaços), mas o uso de um pré-processador (#define) era permitido.

Os resultados são publicados no site de matemática . Ao mesmo tempo, confira o design do site de um matemático real. Os resultados estão aqui . Aqui está o texto do programa, que ficou em segundo lugar, fornecendo o número sobre

$$

$$f_ {w ^ w} (10 ^ {500})$$

 typedef int J; JP(J x,J y) { return x+y ? x%2 + y%2*2 + P(x/2,y/2)*4 : 0 ;} JH(J z) { return z ? z%2 + 2*H(z/4) : 0 ;} JI(J f,J e,J r){ return f ? P(P(f,e),r) : r ;} JM(J x,J e) { return x ? I(x%2, M(e,0), M(x/2, e+1)) : 0 ;} JD(J,J); JE(J f,J e,J r,J b) { return e ? E(1, D(e,b), I(b-1, D(e,b), I(f-1,e,r)), b) : I(f-1,e,r) ; } JD(J x,J b) { return x ? E( H(H(x)), H(H(x)/2), H(x/2), b) : 0 ;} JF(J x,J b) { return x ? F(D(x,b+1),b+1) : b ;} JG(J x) { return F(M(x,9), 9) ;} J f(J n,J x) { return n ? f(n-1, G(x ? f(n,x-1) : n)) : G(x) ;} J g(J x) { return f(x,x) ;} J h(J n,J x) { return n ? h(n-1, g(x ? h(n,x-1) : n)) : g(x) ;} J main(void) { return h(g(9),9) ;} 

O texto do programa do vencedor é mais longo, eu só queria mostrar onde ele começa:

 #define R { return #define PP ( #define LL ( #define TS (v, y, c, #define C ), #define X x) #define F );} 

Mas mesmo o organizador do concurso achou difícil avaliar o tamanho do número (escrito muito grande )

Castores ocupados

Ok, o suficiente para lidar com pequenos números, vamos fazer grandes. Imagine que um concurso universal foi organizado para escrever um programa para gerar o maior número. Como o número de programas não excede 512 caracteres, é claro, sempre há um vencedor absoluto. Vamos designar como BB (512) - função castor ocupado .

É claro que BB (1024) >> BB (512). Mas com que rapidez a função BB cresce? Acontece que está crescendo mais rápido do que tudo o que conhecemos. A função BB em si é algoritmicamente insolúvel; não pode ser calculada em um computador. Porém, à medida que a duração do programa válido aumenta, podemos implementar mais e mais novas idéias. Portanto, o BB cresce mais rápido do que qualquer função algoritmicamente decidível.

PÉ GRANDE

Ok, o suficiente para lidar com pequenos números, vamos fazer grandes. Ah, eu já disse isso? Seria legal rodar BB (BB (n)). Mas como o BB não é computável, há dificuldades técnicas com isso (essa função é computável em máquinas de Turing com oráculos - para não confundir oráculos com o Oracle DBMS).

Mas você pode facilitar, em vez de um programa, considerar uma fórmula com quantificadores de comprimento n. Uma fórmula quantificadora não importa se algo é computável ou não. Portanto, você pode pelo menos assumir a função BB (1.000.000.000) e aplicá-la a si mesmo BB (BB (BB (1.000.000))) vezes. E isso é apenas o que primeiro veio à mente.

O maior número que pode ser indicado por uma fórmula com no máximo n caracteres é indicado por FOOT (n).

$$

$$PÉ GRANDE = PÉ ^ {10} (10 ^ {100})$$

PS

Para o próximo artigo, eu gostaria de entender em que focar, participar da pesquisa, por favor