🧒🏾 👩🏻‍🤝‍👨🏿 🥫 Diminuição no tamanho da amostra de dados experimentais sem perda de informações 📚 🕓 ⁉️

Qual é o problema dos histogramas de dados experimentais

A base do gerenciamento da qualidade do produto de qualquer empresa industrial é a coleta de dados experimentais com o processamento subsequente.

O processamento inicial dos resultados experimentais envolve a comparação das hipóteses sobre a lei da distribuição dos dados, que descrevem, com o menor erro, uma variável aleatória sobre a amostra observada.

Para isso, a amostra é apresentada na forma de um histograma composto por

k

$k$ colunas construídas em intervalos de comprimento

d

$d$ .

A identificação da forma da distribuição dos resultados da medição também exige vários problemas cuja eficiência da solução difere para diferentes distribuições (por exemplo, usando o método dos mínimos quadrados ou calculando as estimativas de entropia).

Além disso, a identificação da distribuição também é necessária porque a dispersão de todas as estimativas (desvio padrão, excesso, curtose etc.) também depende da forma da lei de distribuição.

O sucesso da identificação da forma de distribuição dos dados experimentais depende do tamanho da amostra e, se for pequeno, os recursos de distribuição são mascarados pela aleatoriedade da própria amostra. Na prática, não é possível fornecer um grande tamanho de amostra, por exemplo, mais de 1000, por vários motivos.

Em tal situação, é importante distribuir os dados da amostra da melhor maneira nos intervalos, quando a série de intervalos for necessária para análises e cálculos adicionais.

Portanto, para uma identificação bem-sucedida, é necessário resolver o problema de atribuir o número de intervalos k

A. Hald no livro [1] convence extensivamente que existe um número ideal de intervalos de agrupamento quando o envelope em etapas do histograma construído nesses intervalos é o mais próximo da curva de distribuição suave da população em geral.

Um dos sinais práticos de se aproximar do ótimo é o desaparecimento de quedas no histograma e, em seguida, o maior k é considerado próximo ao ideal, no qual o histograma ainda mantém um caráter suave.

Obviamente, o tipo de histograma depende da construção de intervalos de pertencimento a uma variável aleatória; no entanto, mesmo no caso de uma partição uniforme, um método satisfatório para essa construção ainda não está disponível.

A partição, que pode ser considerada correta, leva ao fato de que o erro de aproximação pela função constante por partes da densidade de distribuição supostamente contínua (histograma) será mínimo.

As dificuldades são causadas pelo fato de a densidade estimada ser desconhecida; portanto, o número de intervalos afeta fortemente a forma da distribuição de frequências da amostra final.

Para um comprimento fixo de amostra, o aumento dos intervalos de partição leva não apenas a um refinamento da probabilidade empírica de penetrá-los, mas também a uma inevitável perda de informações (tanto no sentido geral quanto no sentido da curva de distribuição de densidade de probabilidade), portanto, com o aumento injustificado, a distribuição estudada é muito suavizada. .

Uma vez criada, a tarefa de dividir otimamente o intervalo sob o histograma não desaparece do campo de visão dos especialistas e, até que apareça a única opinião estabelecida sobre sua solução, a tarefa permanecerá relevante.

Escolha de critérios para avaliar a qualidade do histograma dos dados experimentais

O critério de Pearson, como é conhecido, requer a divisão da amostra em intervalos - é neles que se avalia a diferença entre o modelo adotado e a amostra comparada.

c h i^{2} = s u m_{j = 1}^{m} f r a c (E_{j} - M_{j})^{2} M_{j}

$\ chi ^ {2} = \ sum_ {j = 1} ^ {m} \ frac {(E_ {j} -M_ {j}) ^ {2}} {M_ {j}}$

onde:

E_{j}

$E_ {j}$ - frequências experimentais

(n_{j})

$(n_ {j})$ ;

M_{j}

$M_ {j}$ - valores de frequência na mesma coluna; número m de colunas do histograma.

No entanto, a aplicação deste critério no caso de intervalos de comprimento constante, geralmente usados para construir histogramas, é ineficiente. Portanto, nos trabalhos sobre a efetividade do critério de Pearson, os intervalos são considerados não com igual comprimento, mas com igual probabilidade de acordo com o modelo aceito.

Nesse caso, no entanto, o número de intervalos de igual comprimento e o número de intervalos de igual probabilidade diferem várias vezes (com exceção de uma distribuição igualmente provável), o que permite duvidar da confiabilidade dos resultados obtidos em [2].

Como critério de proximidade, é aconselhável usar o coeficiente de entropia, calculado da seguinte forma [3]:

k_{e} = f r a c d n 2 s i g m a 10^{b e t a}

$k_ {e} = \ frac {dn} {2 \ sigma} 10 ^ {\ beta}$

b e t a = - f r a c 1 n s u m_{i = 1}^{m} n_{i} l g (n_{i})

$\ beta = - \ frac {1} {n} \ sum_ {i = 1} ^ {m} {n_ {i} lg (n_ {i})}$

onde:

n_{i}

$n_ {i}$ - o número de observações no i-ésimo intervalo

i = 0, . . ., m

$i = 0, ..., m$

Algoritmo para avaliar a qualidade do histograma dos dados experimentais usando o coeficiente de entropia e o módulo numpy.histogram

A sintaxe para usar o módulo é a seguinte [4]:

numpy.histogram (a, compartimentos = m, intervalo = Nenhum, normed = Nenhum, pesos = Nenhum, densidade = Nenhum)

Consideraremos métodos para encontrar o número ideal m de intervalos de divisão do histograma implementados no módulo numpy.histogram:

• 'auto' - classificações máximas de 'sturges' e 'fd' , fornece bom desempenho;
• 'fd' (Freedman Diaconis Estimator) - um avaliador confiável (resistente a emissões) que leva em consideração a variabilidade e o tamanho dos dados;
• 'doane' - uma versão aprimorada da estimativa de sturges que funciona com mais precisão com conjuntos de dados com uma distribuição não normal;
• 'scott' é um avaliador menos confiável que leva em consideração a variabilidade e o tamanho dos dados;
• 'pedra' - o avaliador é baseado em uma verificação cruzada da estimativa do quadrado do erro, pode ser considerado como uma generalização da regra de Scott;
• 'arroz' - o avaliador não leva em consideração a variabilidade, mas apenas o tamanho dos dados, geralmente superestima o número de intervalos necessários;
• 'sturges' - o método (por padrão), levando em consideração apenas o tamanho dos dados, é ideal apenas para dados gaussianos e subestima o número de intervalos para grandes conjuntos de dados não gaussianos;
• 'sqrt' é o estimador de raiz quadrada do tamanho dos dados usado pelo Excel e outros programas para cálculos rápidos e fáceis do número de intervalos.

Para começar a descrição do algoritmo, adaptamos o módulo numpy.histogram () para calcular o coeficiente de entropia e o erro de entropia:

from numpy import* def diagram(a,m,n): z=histogram(a, bins=m) if type(m) is str:#       m=len(z[0]) y=z[0] d=z[1][1]-z[1][0]#   h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)#  ke=h/std (a)#    (1). return ke,h

Agora considere os principais estágios do algoritmo:

1) Formamos uma amostra de controle (doravante denominada "amostra grande") que atende aos requisitos para o erro no processamento de dados experimentais . A partir de uma amostra grande, removendo todos os membros ímpares, formamos uma amostra menor (a seguir denominada "amostra pequena");

2) Para todos os avaliadores 'auto', 'fd', 'doane', 'scott', 'pedra', 'arroz', 'sturges', 'sqrt', calculamos o coeficiente de entropia ke1 e o erro h1 para uma amostra grande e o coeficiente de entropia ke2 e o erro h2 para uma amostra pequena, bem como o valor absoluto da diferença - abs (ke1-ke2);

3) Controlando os valores numéricos dos avaliadores no nível de pelo menos quatro intervalos, selecionamos o avaliador que fornece o valor mínimo da diferença absoluta - abs (ke1-ke2).

4) Para a decisão final sobre a escolha de um avaliador, construímos em um histograma as distribuições para amostras grandes e pequenas, com o avaliador fornecendo o valor mínimo de abs (ke1-ke2) e no segundo com o avaliador fornecendo o valor máximo de abs (ke1-ke2). O aparecimento de saltos adicionais em uma pequena amostra no segundo histograma confirma a escolha correta do avaliador no primeiro.

Considere o trabalho do algoritmo proposto em uma amostra de dados de uma publicação [2]. Os dados foram obtidos pela seleção aleatória de 80 espaços em branco de 500, com subsequente medição de sua massa. A peça de trabalho deve ter uma massa nos seguintes limites:

m = 17_{- 0, 4}^{+ 0, 6}

$m = 17 _ {- 0,4} ^ {+ 0,6}$ kg Determinamos os parâmetros ideais do histograma usando a seguinte listagem:

Listagem

 import matplotlib.pyplot as plt from numpy import* def diagram(a,m,n): z=histogram(a, bins=m) if type(m) is str:#      m=len(z[0]) y=z[0] d=z[1][1]-z[1][0]#   h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)#   ke=h/std (a)#  return ke,h a =array([17.37, 17.06, 16.96, 16.83, 17.34, 17.45, 17.60, 17.30, 17.02, 16.73, 17.08, 17.28, 17.08, 17.21, 17.29,17.47, 16.84, 17.39, 16.95, 16.92, 17.59, 17.28, 17.31, 17.25, 17.43,17.30, 17.18, 17.26, 17.19, 17.09,16.61, 17.16, 17.17, 17.06, 17.09,16.83, 17.17, 17.06, 17.59, 17.37,17.09, 16.94, 16.76, 16.98, 16.70, 17.27, 17.48, 17.21, 16.74, 17.12,17.33, 17.15, 17.56, 17.45, 17.49,16.94, 17.28, 17.09, 17.39, 17.05, 16.97, 17.16, 17.38, 17.23, 16.87,16.84, 16.94, 16.90, 17.27, 16.93,17.25, 16.85, 17.41, 17.37, 17.50,17.13, 17.16, 17.05, 16.68, 17.56 ] ) c=['auto','fd','doane','scott','stone','rice','sturges','sqrt'] n=len(a) b=[a[i] for i in arange(0,len(a),1) if not i%2 == 0] n1=len(b) print("     (n=80) : %s"%round(std(a),3)) print("    (n=80):%s"%round(mean(a),3)) print("     (n=40): %s"%round(std(b),3)) print("   (n=40): %s"%round(mean(b),3)) u=[] for m in c: ke1,h1=diagram(a,m,n) ke2,h2=diagram(b,m,n1) u.append(abs(ke1-ke2)) print("ke1=%s,h1=%s,ke2=%s,h2=%s,dke=%s,m=%s"%(round(ke1,3),round(h1,3),round(ke2,3),round(h2,3),round(abs(ke1-ke2),3),m)) u1=min(u) c1=c[u.index(min(u))] u2=max(u) c2=c[u.index(max(u))] plt.title(' : %s \n    abs(ke1-ke2) :%s '%(c1,round(u1,3))) plt.hist(a,bins=str(c1)) plt.hist(b,bins=str(c1)) plt.grid() plt.show() plt.title('  : %s \n    abs(ke1-ke2):%s '%(c2,round(u2,3))) plt.hist(a,bins=str(c2)) plt.hist(b,bins=str(c2)) plt.grid() plt.show()

Temos:

O desvio padrão para a amostra (n = 80): 0,24
A expectativa matemática para a amostra (n = 80): 17.158
O desvio padrão para a amostra (n = 40): 0,202
A expectativa matemática da amostra (n = 40): 17.138
ke1 = 1,95, h1 = 0,467, ke2 = 1,917, h2 = 0,387, dke = 0,033, m = automático
ke1 = 1,918, h1 = 0,46, ke2 = 1,91, h2 = 0,386, dke = 0,008, m = fd
ke1 = 1,831, h1 = 0,439, ke2 = 1,917, h2 = 0,387, dke = 0,086, m = doane
ke1 = 1,918, h1 = 0,46, ke2 = 1,91, h2 = 0,386, dke = 0,008, m = scott
ke1 = 1,889, h1 = 0,455, ke2 = 1,934, h2 = 0,39, dke = 0,036, m = pedra
ke1 = 1,831, h1 = 0,439, ke2 = 1,917, h2 = 0,387, dke = 0,086, m = arroz
ke1 = 1,95, h1 = 0,467, ke2 = 1,917, h2 = 0,387, dke = 0,033, m = estouros
ke1 = 1,831, h1 = 0,439, ke2 = 1,917, h2 = 0,387, dke = 0,086, m = sqrt

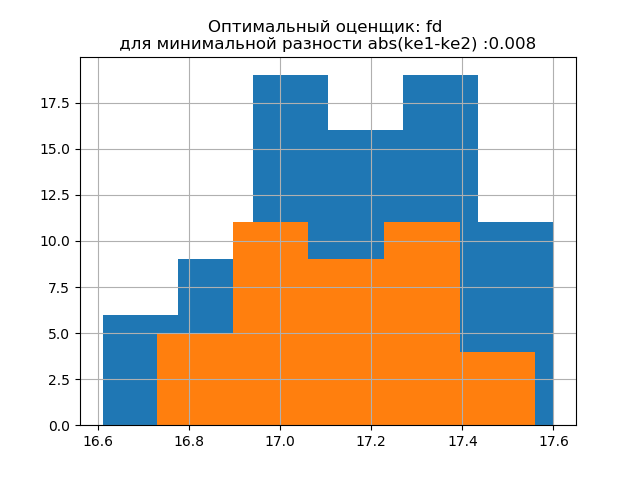
A forma de distribuição de uma amostra grande é semelhante à forma de distribuição de uma amostra pequena. Como segue o script, 'fd' é um avaliador confiável (resistente a emissões) que leva em consideração a variabilidade e o tamanho dos dados. Nesse caso, o erro de entropia da amostra pequena diminui um pouco: h1 = 0,46, h2 = 0,386, com uma ligeira diminuição no coeficiente de entropia de k1 = 1,918 para k2 = 1,91.

Os padrões de distribuição de amostras grandes e pequenas diferem. Como a descrição sugere, 'doane' é uma versão aprimorada da pontuação de 'sturges' que funciona melhor com conjuntos de dados com uma distribuição não normal. Em ambas as amostras, o coeficiente de entropia é próximo a dois e a distribuição é próxima do normal.O aparecimento de saltos adicionais em uma amostra pequena neste histograma, em comparação com a anterior, indica adicionalmente a escolha correta do avaliador 'fd' .

Geramos duas novas amostras para a distribuição normal com os parâmetros mu = 20, sigma = 0,5 e tamanho = 100 usando a relação:

 a= list([round(random.normal(20,0.5),3) for x in arange(0,100,1)])

O método desenvolvido é aplicável à amostra obtida usando o seguinte programa:

Listagem

 import matplotlib.pyplot as plt from numpy import* def diagram(a,m,n): z=histogram(a, bins=m) if type(m) is str:#      m=len(z[0]) y=z[0] d=z[1][1]-z[1][0]#   h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)#   ke=h/std (a)#  return ke,h #a= list([round(random.normal(20,0.5),3) for x in arange(0,100,1)]) a=array([20.525, 20.923, 18.992, 20.784, 20.134, 19.547, 19.486, 19.346, 20.219, 20.55, 20.179,19.767, 19.846, 20.203, 19.744, 20.353, 19.948, 19.114, 19.046, 20.853, 19.344, 20.384, 19.945,20.312, 19.162, 19.626, 18.995, 19.501, 20.276, 19.74, 18.862, 19.326, 20.889, 20.598, 19.974,20.158, 20.367, 19.649, 19.211, 19.911, 19.932, 20.14, 20.954, 19.673, 19.9, 20.206, 20.898, 20.239, 19.56,20.52, 19.317, 19.362, 20.629, 20.235, 20.272, 20.022, 20.473, 20.537, 19.743, 19.81, 20.159, 19.372, 19.998,19.607, 19.224, 19.508, 20.487, 20.147, 20.777, 20.263, 19.924, 20.049, 20.488, 19.731, 19.917, 19.343, 19.26,19.804, 20.192, 20.458, 20.133, 20.317, 20.105, 20.384, 21.245, 20.191, 19.607, 19.792, 20.009, 19.526, 20.37,19.742, 19.019, 19.651, 20.363, 21.08, 20.792, 19.946, 20.179, 19.8]) c=['auto','fd','doane','scott','stone','rice','sturges','sqrt'] n=len(a) b=[a[i] for i in arange(0,len(a),1) if not i%2 == 0] n1=len(b) print("     (n=100):%s"%round(std(a),3)) print("    (n=100):%s"%round(mean(a),3)) print("     (n=50):%s"%round(std(b),3)) print("   (n=50): %s"%round(mean(b),3)) u=[] for m in c: ke1,h1=diagram(a,m,n) ke2,h2=diagram(b,m,n1) u.append(abs(ke1-ke2)) print("ke1=%s,h1=%s,ke2=%s,h2=%s,dke=%s,m=%s"%(round(ke1,3),round(h1,3),round(ke2,3),round(h2,3),round(abs(ke1-ke2),3),m)) u1=min(u) c1=c[u.index(min(u))] u2=max(u) c2=c[u.index(max(u))] plt.title(' : %s \n    abs(ke1-ke2) :%s '%(c1,round(u1,3))) plt.hist(a,bins=str(c1)) plt.hist(b,bins=str(c1)) plt.grid() plt.show() plt.title('  : %s \n    abs(ke1-ke2):%s '%(c2,round(u2,3))) plt.hist(a,bins=str(c2)) plt.hist(b,bins=str(c2)) plt.grid() plt.show()

Temos:
O desvio padrão para a amostra (n = 100): 0,524
A expectativa matemática para a amostra (n = 100): 19,992
O desvio padrão para a amostra (n = 50): 0,462
A expectativa matemática da amostra (n = 50): 20.002
ke1 = 1,979, h1 = 1,037, ke2 = 2,004, h2 = 0,926, dke = 0,025, m = automático
ke1 = 1,979, h1 = 1,037, ke2 = 1,915, h2 = 0,885, dke = 0,064, m = fd
ke1 = 1,979, h1 = 1,037, ke2 = 1,804, h2 = 0,834, dke = 0,175, m = doane
ke1 = 1,943, h1 = 1,018, ke2 = 1,934, h2 = 0,894, dke = 0,009, m = scott
ke1 = 1,943, h1 = 1,018, ke2 = 1,804, h2 = 0,834, dke = 0,139, m = pedra
ke1 = 1,946, h1 = 1,02, ke2 = 1,804, h2 = 0,834, dke = 0,142, m = arroz
ke1 = 1,979, h1 = 1,037, ke2 = 2,004, h2 = 0,926, dke = 0,025, m = sturges
ke1 = 1,946, h1 = 1,02, ke2 = 1,804, h2 = 0,834, dke = 0,142, m = sqrt

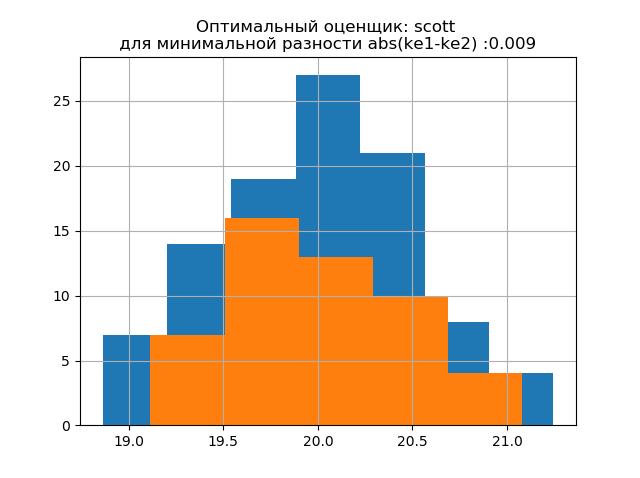
A forma de distribuição de uma amostra grande é semelhante à forma de distribuição de uma amostra pequena. Como segue a descrição, 'scott' é um avaliador menos confiável que leva em consideração a variabilidade e o tamanho dos dados. Nesse caso, o erro de entropia da amostra pequena diminui um pouco: h1 = 1.018 e h2 = 0,894 com uma ligeira diminuição no coeficiente de entropia de k1 = 1,943 a k2 = 1,934. . Deve-se notar que, para a nova amostra, temos a mesma tendência de alterar os parâmetros que no exemplo anterior.

Os padrões de distribuição de amostras grandes e pequenas diferem. Como segue a descrição, 'doane' é uma versão aprimorada da estimativa de 'sturges' , que trabalha com mais precisão com conjuntos de dados com uma distribuição não normal. Nas duas amostras, a distribuição é normal. O aparecimento de saltos adicionais em uma pequena amostra neste histograma em comparação com a anterior indica adicionalmente a escolha correta do avaliador 'scott' .

O uso de anti-aliasing para análise comparativa de histogramas

Suavizar os histogramas construídos nas amostras grandes e pequenas permite determinar com mais precisão sua identidade do ponto de vista da preservação das informações contidas em uma amostra maior. Imagine os dois últimos histogramas como funções de suavização:

Listagem

 from numpy import* from scipy.interpolate import UnivariateSpline from matplotlib import pyplot as plt a =array([20.525, 20.923, 18.992, 20.784, 20.134, 19.547, 19.486, 19.346, 20.219, 20.55, 20.179,19.767, 19.846, 20.203, 19.744, 20.353, 19.948, 19.114, 19.046, 20.853, 19.344, 20.384, 19.945, 20.312, 19.162, 19.626, 18.995, 19.501, 20.276, 19.74, 18.862, 19.326, 20.889, 20.598, 19.974,20.158, 20.367, 19.649, 19.211, 19.911, 19.932, 20.14, 20.954, 19.673, 19.9, 20.206, 20.898, 20.239, 19.56,20.52, 19.317, 19.362, 20.629, 20.235, 20.272, 20.022, 20.473, 20.537, 19.743, 19.81, 20.159, 19.372, 19.998,19.607, 19.224, 19.508, 20.487, 20.147, 20.777, 20.263, 19.924, 20.049, 20.488, 19.731, 19.917, 19.343, 19.26,19.804, 20.192, 20.458, 20.133, 20.317, 20.105, 20.384, 21.245, 20.191, 19.607, 19.792, 20.009, 19.526, 20.37,19.742, 19.019, 19.651, 20.363, 21.08, 20.792, 19.946, 20.179, 19.8]) b=[a[i] for i in arange(0,len(a),1) if not i%2 == 0] plt.title('    \n  abs(ke1-ke2)' ,size=12) z=histogram(a, bins="fd") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label='  n=100') z=histogram(b, bins="fd") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label='  n=50') plt.legend(loc='best') plt.grid() plt.show() plt.title('    \n  abs(ke1-ke2)' ,size=12) z=histogram(a, bins="doane") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label='  n=100') z=histogram(b, bins="doane") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label='  n=50') plt.legend(loc='best') plt.grid() plt.show()

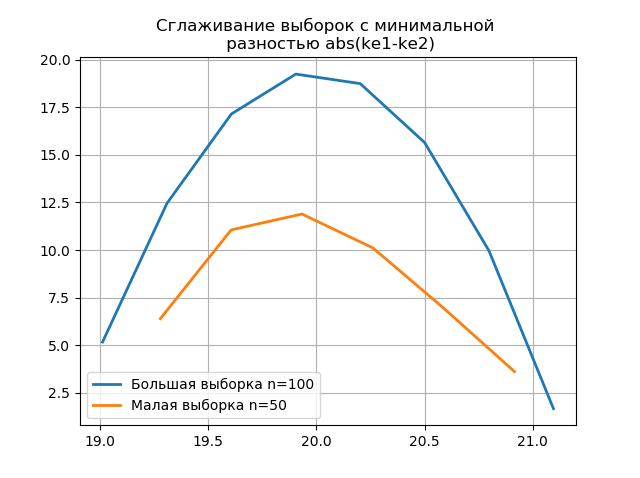
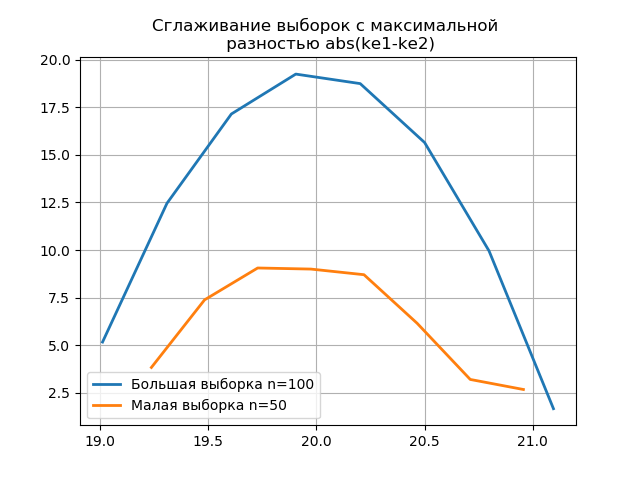
A aparência de saltos adicionais em uma pequena amostra no gráfico de um histograma suavizado em comparação com o anterior indica adicionalmente a escolha correta do avaliador de scott .

Conclusões

Os cálculos apresentados no artigo no intervalo de pequenas amostras comuns na produção confirmaram a eficiência do uso do coeficiente de entropia como critério para manter o conteúdo de informações da amostra e reduzir seu volume . A técnica de usar a versão mais recente do módulo numpy.histogram com avaliadores internos é considerada - 'auto', 'fd', 'doane', 'scott', 'stone', 'rice', 'sturges', 'sqrt', que são suficientes para otimização análise de dados experimentais em estimativas de intervalo.

Referências:

1. Hald A. Estatística matemática com aplicações técnicas. - Moscou: Editora. lit., 1956
2. Kalmykov V.V., Antonyuk F.I., Zenkin N.V.
Determinação do número ideal de classes de agrupamento de dados experimentais para estimativas de intervalos // Boletim Científico da Sibéria do Sul. - 2014. - No. 3. - P. 56-58.
3. Novitsky P. V. O conceito do valor da entropia do erro // Técnica de medição - 1966. - Nº 7. - S. 11-14.
4.numpy.histogram - Manual do NumPy v1.16

Diminuição no tamanho da amostra de dados experimentais sem perda de informações

Qual é o problema dos histogramas de dados experimentais

Escolha de critérios para avaliar a qualidade do histograma dos dados experimentais

Algoritmo para avaliar a qualidade do histograma dos dados experimentais usando o coeficiente de entropia e o módulo numpy.histogram

O uso de anti-aliasing para análise comparativa de histogramas

Conclusões

Referências:

More articles: