1. Introdução

Como descobrir que uma pessoa entendeu o que são mônadas? Ele próprio lhe falará sobre isso nos primeiros 5 minutos de comunicação e certamente tentará explicar. Ele também escreverá um texto a respeito e, se possível, publicará em algum lugar, para que todos os outros também entendam o que são mônadas.

Entre os programadores funcionais, especialmente em Haskell, as mônadas se tornaram um meme local. Eles costumam tentar explicar, começando em casos especiais e dando exemplos de uso imediatamente. Por causa disso, o ouvinte pode não entender a essência principal do conceito, e as mônadas permanecerão como magia negra, bem, ou simplesmente um meio de esmagar os efeitos colaterais em linguagens puramente funcionais.

Primeiro, falarei sobre os conceitos básicos da teoria das categorias e, de um ponto de vista prático, abordaremos a definição de mônada e veremos que muitos programadores usam essa poderosa abstração em uma de suas manifestações.

Minha apresentação é amplamente baseada no livro de Bartosz Milewski, Category Theory for Programmers, que foi criado como uma série de postagens de blog , está disponível em PDF e foi publicado recentemente em papel.

Os exemplos são fornecidos em Haskell, pressupõe-se que o leitor esteja familiarizado com a sintaxe e os conceitos básicos da linguagem. No livro mencionado, existem exemplos em C ++, você pode comparar a pureza e a compreensibilidade do código.

Categorias

Definição de

As categorias em si são construções muito simples. Uma categoria é uma coleção de objetos e morfismos entre eles. Os morfismos podem ser considerados setas unidirecionais que conectam objetos. No caso geral, nada se sabe sobre a essência dos próprios objetos. A teoria das categorias não funciona com objetos, mas com morfismos, ou melhor, com sua composição .

A seguinte notação é usada:

• Ob _C - objetos da categoria C ;
• Hom _C (A, B) - morfismos de A a B;
• g ∘ f é a composição dos morfismos f e g.

Ao definir uma categoria, os morfismos estão sujeitos a restrições adicionais:

1. Para um par de morfismos f e g, se f é um morfismo de A a B (f ∈ Hom (A, B)), g é um morfismo de B a C (g ∈ Hom (B, C)), então existe uma composição g ∘ f é um morfismo de A a C (g ∘ f ∈ Hom (A, C)).
2. Para cada objeto, é fornecido um ID de morfismo de identidade _A ∈ Hom (A, A).

Existem duas propriedades importantes que qualquer categoria deve satisfazer (axiomas da teoria da categoria):

1. A associatividade da composição: h ∘ (g ∘ f) = (h ∘ g) ∘ f;
2. Composição com o morfismo da identidade: se f ∈ Hom (A, B), então f ∘ id _A = id _B ∘ f = f.

As categorias são visualizadas com muita facilidade e natural como gráficos direcionados. Em princípio, qualquer gráfico orientado pode ser estendido a uma categoria adicionando composições de morfismos e morfismos idênticos, se necessário.

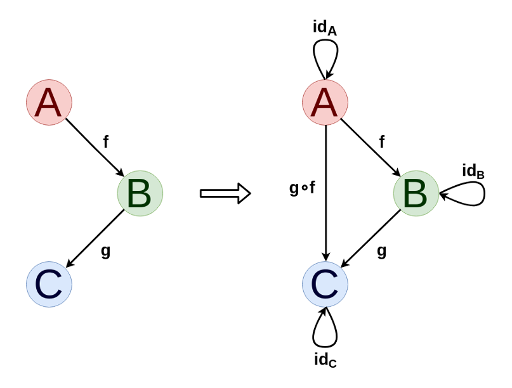
Para qualquer categoria, você pode definir uma categoria dupla (indicada por C ^op , na qual os morfismos são obtidos girando as setas da categoria original e os objetos são os mesmos. Isso nos permite formular declarações e teoremas duplos, cuja verdade não muda quando as setas são invertidas.

Objetos e morfismos não necessariamente formam conjuntos (no sentido clássico, da teoria dos conjuntos); portanto, no caso geral, a frase "classe de objetos" é usada. As categorias nas quais classes de objetos e morfismos ainda são conjuntos são chamadas de categorias pequenas . Além disso, trabalharemos apenas com eles.

Tipos e funções

, Haskell, — . , Int Bool — , Int -> Bool — .

id, :

id :: a -> a
id x = x

— , Haskell :

f :: a -> b
g :: b -> c
g . f :: a -> c
(g . f) x = g (f x)

, , — , Set. , — , : . bottom, _|_. , , , bottom. Haskell, , Hask. , Set. , , : Hom_C(A, B) ∈ C. , a -> b — Haskell.

.

Void, ( ). absurd, , , Void, :

absurd :: Void -> a

Unit, — , (). unit , :

unit :: a -> Unit
unit _ = ()

— Bool:

data Bool = True | False

, Void, Unit Bool.

Void , absurd, Bool, Unit. , Void, , .

Bool -> Unit , unit, . Unit -> Bool . (), True, False. , Unit Bool:

true, false :: a -> Bool
true _ = True
false _ = False

Bool Bool — , 4 ( n — 2²ⁿ): id, true false, , not:

not :: Bool -> Bool
not True = False
not False = True

, :

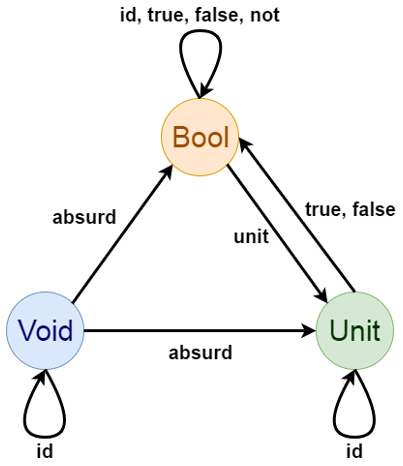
Haskell- .

— . , C D, F . -, C D. a — C, F a — D, . -, : f :: a -> b C F f :: F a -> F b D.

, " " :

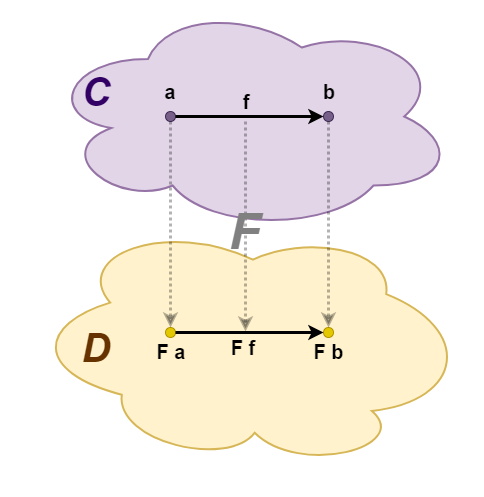
1. h = g ∘ f, F h = F g ∘ F f.
2. id_a — a, F id_a = id_{F a} — F a.

, "" : , , . , , () . , .

. , F :: C -> D G :: D -> E G . F :: C -> E. , , , , . Id_C, Id_D Id_E. , , .

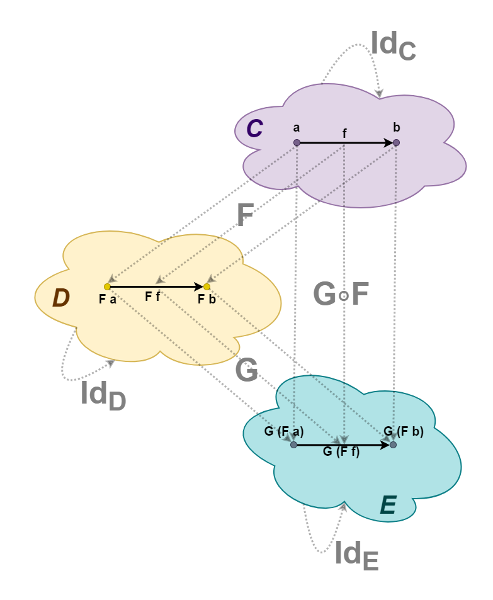
, , -, — (). , Cat ( ).

Haskell . , , - , .

Maybe , a Maybe a ( Maybe !):

data Maybe a = Nothing | Just a

, f :: a -> b F f :: Maybe a -> Maybe b. fmap. , ( ):

--          f                F f
--      /------\    /------------------\
fmap :: (a -> b) -> (Maybe a -> Maybe b)
fmap _ Nothing = Nothing
fmap f (Just x) = Just (f x)

, Maybe — . , , Functor. fmap, , ( — ):

class Functor f where
  fmap :: (a -> b) -> f a -> f b

— , , fmap . f a -> f b, , .

, , , .. , . : , - .

. , . , , — Haskell.

: upCase, , toWords, . toUpper words:

upCase :: String -> String
upCase = map toUpper

toWords :: String -> [String]
toWords = words

:

processString :: String -> [String]
processString = toWords . upCase

, . , processString "upCase toWords".

— , . -, , , -, , .

, a , .

newtype Writer a = Writer (a, String)

, Writer — , fmap:

instance Functor Writer where
  fmap f (Writer (x, s)) = Writer (f x, s)

upCase toWords , , "" Writer:

upCase :: String -> Writer String
upCase s = Writer (map toUpper s, "upCase ")

toWords :: String -> Writer [String]
toWords s = Writer (words s, "toWords ")

, , - . , b , , c c , :

compose :: (a -> Writer b) -> (b -> Writer c) -> (a -> Writer c)
compose f g = \x -> let Writer (y, s1) = f x
                        Writer (z, s2) = g y
                    in Writer (z, s1 ++ s2)

processString :

processString :: String -> [String]
processString = compose upCase toWords

. () a -> b a -> Writer b , a b. , .. a -> Writer a:

writerId :: a -> Writer a
writerId x = Writer (x, "")

, , Hask. , a b a -> b, a -> m b, .. "" - m. (embellished). m, Writer — .

C m. K, , C, .. Ob_K = Ob_C. a -> b K a -> m b C: Hom_K(a, b) = Hom_C(a, m b). , , K — C.

, , , . , m — . Haskell ( Hask):

class Monad m where
  --    
  (>=>)  :: (a -> m b) -> (b -> m c) -> (a -> m c)
  --  
  return :: a -> m a

>=>, "fish", : . , , — , , , . Writer — , compose — >=>, writerId — return.

>=> . , -. a, f, , , bind:

f >=> g = \a -> let mb = f a
                in (bind mb g)
  where
    bind :: m b -> (b -> m c) -> m c

bind b " " m , b m c. >=>. : m b -> (b -> m c) -> m c. , . "" Haskell >>=, bind, return:

class Monad m where
  (>>=)  :: m a -> (a -> m b) -> m b
  return :: a -> m a

, - b -> m c b, m b. , m, fmap, (a -> m b) -> m a -> m (m b). >>= m (m b) m b, "" , . join:

ma >>= g = join (fmap g ma)
  where
    join :: m (m a) -> m a

, Writer :

join :: Writer (Writer a) -> Writer a
join (Writer ((Writer (x, s2)), s1)) = Writer (x, s1 ++ s2)

Monad:

class Functor m => Monad m where
  join   :: m (m a) -> m a
  return :: a -> m a

, m . , fmap >>=:

fmap :: (a -> b) -> m a -> m b
fmap f ma = ma >>= (\a -> return (f a))

, "" .

(.. , ) .

(a -> [b]) -> (b -> [c]) -> (a -> [c]). :

(>=>) :: (a -> [b]) -> (b -> [c]) -> (a -> [c])
f >=> g = \x -> concat (map g (f x))

. a, , — f [b]. , b — g : map g (f x) :: [[c]]. , .

>>= :

(>>=) :: [a] -> (a -> [b]) -> [b]
xs >>= f = concat (map f xs)

return :: a -> [a]. :

return :: a -> [a]
return x = [x]

Monad:

instance Monad [] where
  xs >>= f = concat (map f xs)
  return x = [x]

, . , , . , — , ..

, , - .

, , Maybe. Just, — Nothing. , , :

(>=>) :: (a -> Maybe b) -> (b -> Maybe c) -> (a -> Maybe c)
f >=> g = \x -> case f x of
                  Just y  -> g y
                  Nothing -> Nothing

Monad Maybe:

instance Monad Maybe where
  (Just x) >>= f = f x
  Nothing  >>= f = Nothing
  return x = Just x

, . , - , , - . Either String a, : , . :

data Either a b = Left a | Right b

, . . :

type WithException a = Either String a

Maybe:

(>=>) :: (a -> WithException b) -> (b -> WithException c) -> (a -> WithException c)
f >=> g = \x -> case f x of
                  Right y -> g y
                  err     -> err

Monad :

instance Monad WithException where
  (Right x) >>= f = f x
  err >>= f = err
  return x = Right x

, , write-only , . a -> b , , . , , ( , ):

a -> s -> (b, s)

:

newtype State s a = State (s -> (a, s))

s , State s . runState:

runState :: State s a -> s -> (a, s)
runState (State f) s = f s

Functor:

instance Functor (State s) where
  fmap f state = State st'
    where
     st' prevState = let (a, newState) = runState state prevState
                     in (f a, newState)

, a b, , a -> State s b, State s — . , :

(>=>) :: (a -> State s b) -> (b -> State s c) -> (a -> State s c)
f >=> g = \x -> State (\s -> let (y, s') = runState (f x) s
                             in runState (g y) s')

Monad. , return, , -:

instance Monad (State s) where
  stateA >>= f = State (\s -> let (a, s') = runState stateA s
                              in runState (f a) s')
  return a = State (\s -> (a, s))

, . , Unit s , Unit -> State s s:

get :: Unit -> State s s
get _ = State (\s -> (s, s))

, Unit . , .

, , . , , , s Unit, s -> State s Unit:

put :: s -> State s Unit
put s = State (\_ -> ((), s))

, , /. , " " RealWorld, . RealWorld - , (, ). :

type IO a = State RealWorld a

IO — , Haskell, "". , . , , , -, .