💃🏼 🤥 🧑🏼‍🤝‍🧑🏼 Estados Quânticos Neurais - Representação de uma função de onda por uma rede neural 👩🏿‍🤝‍👩🏼 🙆🏾 👩🏾‍💻

Neste artigo, consideraremos a aplicação incomum de redes neurais em geral e máquinas limitadas de Boltzmann, em particular para resolver dois problemas complexos da mecânica quântica - encontrar a energia do estado fundamental e aproximar a função de onda de um sistema de muitos corpos.

Podemos dizer que esta é uma recontagem gratuita e simplificada de um artigo [2], publicado na Science em 2017 e em alguns trabalhos subsequentes. Não encontrei exposições científicas populares deste trabalho em russo (e apenas esta versão em inglês), embora me parecesse muito interessante.

Conceitos essenciais mínimos da mecânica quântica e aprendizagem profunda

Quero notar imediatamente que essas definições são extremamente simplificadas . Trago-os para aqueles para quem o problema descrito é uma floresta escura.

Um estado é simplesmente um conjunto de quantidades físicas que descrevem um sistema. Por exemplo, para um elétron voando no espaço, serão suas coordenadas e momento, e para uma treliça de cristal, será um conjunto de rotações de átomos localizadas em seus nós.

A função de onda do sistema é uma função complexa do estado do sistema. Uma certa caixa preta que recebe uma entrada, por exemplo, um conjunto de rotações, mas retorna um número complexo. A principal propriedade da função de onda que é importante para nós é que seu quadrado é igual à probabilidade desse estado:

P s i (s) P s i (s)^{*} = P (s)

$\ Psi (s) \ Psi (s) ^ * = P (s)$

É lógico que o quadrado da função de onda seja normalizado para a unidade (e esse também é um dos problemas significativos).

O espaço de Hilbert - no nosso caso, essa definição é suficiente - o espaço de todos os estados possíveis do sistema. Por exemplo, para um sistema de 40 rotações que pode assumir os valores +1 ou -1, o espaço Hilbert é todo

2^{40}

$2 ^ {40}$ condições possíveis. Para coordenadas que podem assumir valores

[- i n f t y, + i n f t y]

$[- \ infty, + \ infty]$ , a dimensão do espaço Hilbert é infinita. É a enorme dimensão do espaço de Hilbert para qualquer sistema real que é o principal problema que não permite resolver equações analiticamente: no processo, haverá integrais / somatórios em todo o espaço de Hilbert que não podem ser calculados "de frente". Um fato curioso: durante toda a vida do Universo, você pode encontrar apenas uma pequena parte de todos os estados possíveis incluídos no espaço Hilbert. Isso é muito bem ilustrado por uma imagem de um artigo sobre a Tensor Networks [1], que mostra esquematicamente todo o espaço de Hilbert e os estados que podem ser encontrados após um polinômio a partir da característica da complexidade do espaço (número de corpos, partículas, giros, etc.)

Uma máquina limitada de Boltzmann - se difícil de explicar, é um modelo probabilístico gráfico não direcionado, cuja limitação é a independência condicional das probabilidades dos nós de uma camada em relação aos nós da mesma camada. Se de uma maneira simples, essa é uma rede neural com uma entrada e uma camada oculta. Os valores da saída dos neurônios na camada oculta podem ser 0 ou 1. A diferença da rede neural usual é que as saídas dos neurônios da camada oculta são variáveis aleatórias selecionadas com uma probabilidade igual ao valor da função de ativação:

P_{i} (1) = s i g m a (b_{i} + s u m_{j} W_{i j} s_{j})

$P_i (1) = \ sigma (b_i + \ sum_jW_ {ij} s_j)$

onde

s i g m a

$\ sigma$ - função de ativação sigmóide ,

b_{i}

$b_i$ - deslocamento para o i-ésimo neurônio,

W

$W$ - o peso da rede neural,

s_{j}

$s_j$ - camada visível. As máquinas limitadas de Boltzmann pertencem aos chamados "modelos de energia", pois podemos expressar a probabilidade de um estado específico de uma máquina usar a energia dessa máquina:

E (v, h) = - a^{T} v - b^{T} h - v^{T} W h

$E (v, h) = -a ^ Tv - b ^ Th - v ^ TWh$

onde v e h são as camadas visíveis e ocultas, a e b são os deslocamentos das camadas visíveis e ocultas, W são os pesos. Então a probabilidade do estado é representável na forma:

P (v, h) = f r a c 1 Z e^{- E (v, h)}

$P (v, h) = \ frac {1} {Z} e ^ {- E (v, h)}$

onde Z é o termo de normalização, também chamado de soma estatística (é necessário para que a probabilidade total seja igual à unidade).

1. Introdução

Hoje, existe uma opinião entre os especialistas em aprendizagem profunda que limitou
Máquinas Boltzmann (daqui em diante - OMB) é um conceito desatualizado que praticamente não é aplicável em tarefas reais. No entanto, em 2017, um artigo [2] apareceu na Science que mostrou o uso muito eficiente do OMB para problemas da mecânica quântica.

Os autores notaram dois fatos importantes que podem parecer óbvios, mas nunca haviam ocorrido a ninguém antes:

OMB é uma rede neural que, de acordo com o teorema universal de Tsybenko , pode teoricamente aproximar qualquer função com precisão arbitrariamente alta (ainda existem muitas restrições, mas você pode ignorá-las).
OMB é um sistema cuja probabilidade de cada estado é função da entrada (camada visível), pesos e deslocamentos da rede neural.

Bem, e mais os autores disseram: deixe nosso sistema ser completamente descrito pela função de onda, que é a raiz da energia OMB, e as entradas OMB são as características do nosso estado do sistema (coordenadas, giros, etc.):

P s i (s) = f r a c 1 Z s q r t e^{E (s, h)}

$\ Psi (s) = \ frac {1} {Z} \ sqrt {e ^ {E (s, h)}}$

onde s são as características do estado (por exemplo, backs), h são as saídas da camada oculta do OMB, E é a energia do OMB, Z é a constante de normalização (soma estatística).

É isso aí, o artigo da Science está pronto, restando apenas alguns pequenos detalhes. Por exemplo, é necessário resolver o problema da função de partição não computável devido ao enorme tamanho do espaço Hilbert. E o teorema de Tsybenko nos diz que uma rede neural pode se aproximar de qualquer função, mas não diz como encontrar um conjunto adequado de pesos e compensações de rede para isso. Bem, e como sempre, a diversão começa aqui.

Modelo de treinamento

Agora, existem algumas modificações na abordagem original, mas vou considerar apenas a abordagem do artigo original [2].

Desafio

No nosso caso, a tarefa de treinamento será a seguinte: encontrar uma aproximação da função de onda que tornaria o estado com energia mínima a mais provável. Isso é intuitivamente claro: a função de onda nos dá a probabilidade de um estado, o valor próprio da Hamiltoniana (o operador de energia, ou ainda mais simples, a energia - esse entendimento é suficiente no quadro deste artigo) para a função de onda ser a energia. Tudo é simples.

Na realidade, procuraremos otimizar outra quantidade, a chamada energia local, que é sempre maior ou igual à energia do estado fundamental:

E_{l o c} (s i g m a) = R e s u m_{s i g m a s i g m a^{'}} H_{s i g m a s i g m a^{'}} f r a c P s i (s i g m a^{'}) P s i (s i g m a)

$E_ {loc} (\ sigma) = Re \ sum _ {\ sigma \ sigma '} H _ {\ sigma \ sigma'} \ frac {\ Psi (\ sigma ')} {\ Psi (\ sigma)}$

aqui

s i g m a

$\ sigma$ É a nossa condição

s i g m a^{'}

$\ sigma '$ - todos os estados possíveis do espaço Hilbert (na realidade, consideraremos um valor mais aproximado),

H_{s i g m a s i g m a^{'}}

$H _ {\ sigma \ sigma '}$ É o elemento da matriz do Hamiltoniano. Muito dependente do Hamiltoniano específico, por exemplo, para o modelo de Ising, isso é apenas

f (s i g m a)

$f (\ sigma)$ se

s i g m a = s i g m a^{'}

$\ sigma = \ sigma '$ e

- c o n s t

$-const$ em todos os outros casos. Não pare aqui agora; é importante que esses elementos possam ser encontrados para vários hamiltonianos populares.

Processo de otimização

Amostragem

Uma parte importante da abordagem do artigo original foi o processo de amostragem. Foi utilizada uma variação modificada do algoritmo Metropolis-Hastings . A linha inferior é:

Começamos de um estado aleatório.
Mudamos o sinal de um giro selecionado aleatoriamente para o oposto (para as coordenadas existem outras modificações, mas elas também existem).
Com probabilidade igual a $P (\ sigma '| \ sigma) = \ Big | {\ frac {\ Psi (\ sigma')} {\ Psi (\ sigma)} \ Big | ^ 2$ , mude para um novo estado.
Repita N vezes.

Como resultado, obtemos um conjunto de estados aleatórios selecionados de acordo com a distribuição que nossa função de onda nos fornece. Você pode calcular os valores de energia em cada estado e a expectativa matemática de energia

m a t h b b E (E_{l o c})

$\ mathbb {E} (E_ {loc})$ .

Pode-se mostrar que a estimativa do gradiente de energia (mais precisamente, o valor esperado do Hamiltoniano) é igual a:

G_{k} (x) = 2 * (E_{l o c} (x) - m a t h b b E (E_{l o c})) * D_{k}^{*} (x)

$G_k (x) = 2 * (E_ {loc} (x) - \ mathbb {E} (E_ {loc})) * D ^ * _ k (x)$

Conclusão

Isto é de uma palestra proferida por G. Carleo em 2017 para a Advanced School on Quantum Science and Quantum Technology. Existem entradas no Youtube.

Denotar:

D_{k}^{*} (x) = f r a c p a r c i a l_{p_{k}} P s i (x) P s i (x)

$D ^ * _ k (x) = \ frac {\ parcial_ {p_k} \ Psi (x)} {\ Psi (x)}$

Então:

p a r c i a l_{p_{k}} m a t h b b E (H) =

$\ parcial_ {p_k} \ mathbb {E} (H) =$

p a r c i a l f r a c s u m_{x x^{'}} P s i^{*} (x) H_{x x^{'}} P s i (x^{'}) s u m_{x} | P s i (x) |^{2} =

$\ parcial \ frac {\ sum_ {xx '} \ Psi ^ * (x) H_ {xx'} \ Psi (x ')} {\ sum_x | \ Psi (x) | ^ 2} =$

f r a c s u m_{x x^{'}} P s i^{*} (x) H_{x x^{'}} D_{k} (x^{'}) P s i (x^{'}) s u m_{x} | P s i (x) |^{2} + f r a c s u m_{x x^{'}} P s i^{*} (x) D_{k}^{*} (x) H_{x x^{'}} P s i (x^{'}) s u m_{x} | P s i (x) |^{2} -

$\ frac {\ sum_ {xx '} \ Psi ^ * (x) H_ {xx'} D_k (x ') \ Psi (x')} {\ sum_x | \ Psi (x) | ^ 2} + \ frac {\ sum_ {xx '} \ Psi ^ * (x) D_k ^ * (x) H_ {xx'} \ Psi (x ')} {\ sum_x | \ Psi (x) | ^ 2} -$

f r a c s u m_{x x^{'}} P s i^{*} (x) H_{x x^{'}} P s i (x^{'}) s u m_{x} | P s i (x) |^{2} f r a c s u m_{x} | P s i (x) |^{2} (D_{k} (x) - D_{k}^{*} (x)) s u m_{x} | P s i (x) |^{2} =

$\ frac {\ sum_ {xx '} \ Psi ^ * (x) H_ {xx'} \ Psi (x ')} {\ sum_x | \ Psi (x) | ^ 2} \ frac {\ sum_x | \ Psi (x) | ^ 2 (D_k (x) - D ^ * _ k (x))} {\ sum_x | \ Psi (x) | ^ 2} =$

f r a c s u m_{x x^{'}} f r a c P s i^{*} (x) P s i^{*} (x^{'}) H_{x x^{'}} D_{k} (x^{'}) | P s i (x^{'}) |^{2} + s u m_{x x^{'}} | P s i (x) |^{2} H_{x x^{'}} D_{k}^{*} (x^{'}) f r a c P s i (x^{'}) P s i (x) s u m_{x} | P s i (x) |^{2} -

$\ frac {\ sum_ {xx '} \ frac {\ Psi ^ * (x)} {\ Psi ^ * (x')} H_ {xx '} D_k (x') | \ Psi (x ') | ^ 2 + \ sum_ {xx '} | \ Psi (x) | ^ 2H_ {xx'} D ^ * _ k (x ') \ frac {\ Psi (x')} {\ Psi (x)}} {\ sum_x | \ Psi (x) | ^ 2} -$

m a t h b b E (H) f r a c s u m_{x} | P s i (x) |^{2} (D_{k} (x) + D_{k}^{*} (x)) s u m_{x} | P s i (x) |^{2} a p p r o x

$\ mathbb {E} (H) \ frac {\ sum_x | \ Psi (x) | ^ 2 (D_k (x) + D ^ * _ k (x))} {\ sum_x | \ Psi (x) | ^ 2 } \ approx$

m a t h b b E (E_{l o c} D_{k}^{*}) - m a t h b b E (E_{l o c}) m a t h b b E (D_{k}^{*}) + C

$\ mathbb {E} (E_ {loc} D ^ * _ k) - \ mathbb {E} (E_ {loc}) \ mathbb {E} (D ^ * _ k) + C$

Depois, resolvemos o problema de otimização:

Amostramos estados do nosso OMB.
Calculamos a energia de cada estado.
Estime o gradiente.
Atualizamos o peso do OMB.

Como resultado, o gradiente de energia tende a zero, o valor da energia diminui, assim como o número de novos estados únicos no processo Metropolis-Hastings, porque, ao coletar amostras da verdadeira função de onda, quase sempre obtemos o estado fundamental. Intuitivamente, isso parece lógico.

No trabalho original para pequenos sistemas, os valores da energia do estado fundamental foram obtidos, muito próximos dos valores exatos obtidos analiticamente. Foi feita uma comparação com as abordagens conhecidas para encontrar a energia do estado fundamental, e o NQS venceu, especialmente considerando a complexidade computacional relativamente baixa do NQS em comparação com os métodos conhecidos.

NetKet - uma biblioteca da abordagem "inventores"

Um dos autores do artigo original [2], com sua equipe, desenvolveu a excelente biblioteca NetKet [3], que contém um kernel C muito otimizado (na minha opinião), bem como a API Python, que trabalha com abstrações de alto nível.

A biblioteca pode ser instalada via pip. Os usuários do Windows 10 terão que usar o Linux Subsystem for Windows.

Vamos considerar trabalhar com a biblioteca como um exemplo de uma cadeia de 40 rotações assumindo os valores + -1 / 2. Vamos considerar o modelo de Heisenberg, que leva em consideração as interações vizinhas.

O NetKet possui uma excelente documentação que permite descobrir rapidamente o que e como fazer. Existem muitos modelos embutidos (costas, bósons, modelos Ising, Heisenberg, etc.) e a capacidade de descrever completamente o modelo.

Contagem Descrição

Todos os modelos são apresentados em gráficos. Para nossa cadeia, o modelo Hypercube integrado com uma dimensão e condições de contorno periódicas é adequado:

import netket as nk graph = nk.graph.Hypercube(length=40, n_dim=1, pbc=True)

Descrição do Hilbert Space

Nosso espaço Hilbert é muito simples - todos os giros podem receber valores +1/2 ou -1/2. Nesse caso, o modelo interno para rotações é adequado:

 hilbert = nk.hilbert.Spin(graph=graph, s=0.5)

Descrição do Hamiltoniano

Como já escrevi, no nosso caso, o Hamiltoniano é o Hamiltoniano de Heisenberg, para o qual existe um operador interno:

 hamiltonian = nk.operator.Heisenberg(hilbert=hilbert)

Descrição do RBM

No NetKet, você pode usar uma implementação RBM pronta para rotações - este é apenas o nosso caso. Mas, em geral, existem muitos carros, você pode tentar carros diferentes.

 nk.machine.RbmSpin(hilbert=hilbert, alpha=4) machine.init_random_parameters(seed=42, sigma=0.01)

Aqui alfa é a densidade dos neurônios na camada oculta. Para 40 neurônios do visível e do alfa 4, haverá 160. Existe outra maneira de indicar diretamente pelo número. O segundo comando inicializa pesos aleatoriamente de

N (0, s i g m a)

$N (0, \ sigma)$ . No nosso caso, sigma é 0,01.

Samler

Um amostrador é um objeto que nos será devolvido por uma amostra de nossa distribuição, que é dada pela função de onda no espaço Hilbert. Usaremos o algoritmo Metropolis-Hastings descrito acima, modificado para nossa tarefa:

 sampler = nk.sampler.MetropolisExchangePt( machine=machine, graph=graph, d_max=1, n_replicas=12 )

Para ser mais preciso, o amostrador é um algoritmo mais complicado que o descrito acima. Aqui, verificamos simultaneamente até 12 opções em paralelo para selecionar o próximo ponto. Mas o princípio, em geral, é o mesmo.

Optimizer

Isso descreve o otimizador que será usado para atualizar os pesos do modelo. Com base na experiência pessoal de trabalhar com redes neurais em áreas que lhes são mais "familiares", a melhor e mais confiável opção é a boa e velha descida do gradiente estocástico por um momento (bem descrito aqui ):

 opt = nk.optimizer.Momentum(learning_rate=1e-2, beta=0.9)

Treinamento

O NetKet tem treinamento sem um professor (nosso caso) e com um professor (por exemplo, a chamada “tomografia quântica”, mas esse é o tópico de um artigo separado). Simplesmente descrevemos os "professores" e é isso:

 vc = nk.variational.Vmc( hamiltonian=hamiltonian, sampler=sampler, optimizer=opt, n_samples=1000, use_iterative=True )

O Monte Carlo variacional indica como avaliamos o gradiente da função que estamos otimizando. n_smaples é o tamanho da amostra da nossa distribuição que o amostrador retorna.

Resultados

Executaremos o modelo da seguinte maneira:

 vc.run(output_prefix=output, n_iter=1000, save_params_every=10)

A biblioteca é construída usando o OpenMPI, e o script precisará ser executado assim: mpirun -n 12 python Main.py (12 é o número de núcleos).

Os resultados que recebi são os seguintes:

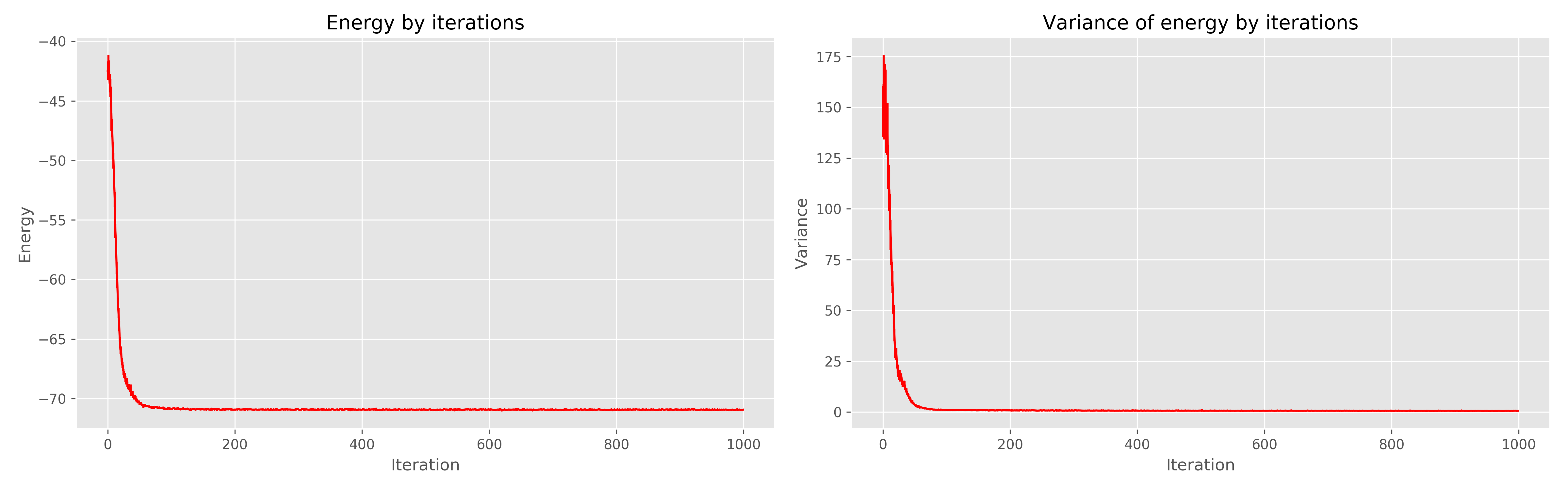
À esquerda, o gráfico de energia da era da aprendizagem, à direita, a dispersão de energia da era da aprendizagem.
Pode-se ver que 1000 eras são claramente redundantes, já seriam suficientes 300. Em geral, funciona muito bem, converge rapidamente.

Literatura

Orús R. Uma introdução prática a redes tensoras: estados de produtos matriciais e estados de pares emaranhados projetados // Annals of Physics. - 2014 .-- T. 349. - S. 117-158.
Carleo G., Troyer M. Resolvendo o problema quântico de muitos corpos com redes neurais artificiais // Science. - 2017. - T. 355. - Não. 6325. - S. 602-606.
www.netket.org

Estados Quânticos Neurais - Representação de uma função de onda por uma rede neural