Catálise de Muon em termos de química quântica. Parte II: eletrônico vs. ligação química do múon

Mnogabukaff afirma que a química quântica pensa no princípio da catálise do múon: como exatamente o múon baixa a temperatura do plasma desejado. Em duas partes (a primeira parte pode ser lida aqui ).

A essência da segunda parte é simples: o múon é mais pesado que o elétron, por isso fornece uma ligação química mais forte e uma abordagem mais próxima dos núcleos, diminuindo assim a temperatura plasmática necessária para iniciar a reação termonuclear.

Mas aqueles que querem olhar para as fórmulas, gráficos e ver a essência conceitual da química quântica aplicada às moléculas mais simples (quase), bem-vindas ao gato.

1. Introdução

Na primeira parte (veja aqui ), examinamos a diferença entre um átomo de hidrogênio $$$\ mathrm {H} ^ \ cdot = \ mathrm {p ^ + e ^ -}$ do seu homólogo pesado muon $$$\ mathrm {p} ^ + \ mu ^ -$ : no segundo caso, o múon será amarrado com mais força e ficará a uma distância mais próxima do próton. Ao mesmo tempo, examinamos algumas coisas importantes que precisaremos aqui (formas de orbitais e sistema atômico de unidades).

Na segunda parte (isto é, aqui), tentaremos entender por que, como e quanto a temperatura do plasma necessária para inflamar a reação termonuclear diminuirá. As reações que nos interessam são:

$$

$$\ mathrm {{} ^ nH + {} ^ m H \ rightarrow} \ \ text {novos kernels + energia}$$

onde n, m = 1,2,3 corresponde a próton, deutério e trítio, respectivamente. Naturalmente, esses núcleos têm uma carga positiva; portanto, se você tentar aproximá-los, eles começarão a se repelir de acordo com a lei de Coulomb (veja a parte anterior ), e essa é a barreira que impede o aparecimento de reações de fusão. A propósito, no caso de reações de decaimento nuclear, essa repulsão tem o papel oposto, porque após a separação do núcleo comum, os fragmentos, repelindo um ao outro, adquirem energia cinética adicional, e é essa energia que é aquecida nas usinas nucleares.

Para superar essa barreira de Coulomb, é necessário um aumento na temperatura do plasma ( T ), que, como todos se lembram do curso escolar do MKT , está associado à velocidade média das partículas no plasma ( v ) pela fórmula

$$

$$mv ^ 2 = 3k_ \ mathrm {B} T$$

onde m é a massa de partículas e $$$k_ \ mathrm {B}$ - constante de Boltzmann .

Mas, vamos imaginar que combinamos dois núcleos de hidrogênio em uma determinada partícula, onde eles já estão localizados próximos e, portanto, o restante da barreira para eles já é muito pequeno. Então precisaríamos acelerar significativamente essas partículas (leia-se: precisamos de temperaturas mais baixas) para combiná-las em algo novo. E apenas esse papel deve desempenhar um íon intermediário $$$(\ mathrm {{} ^ nH} \ mu ^ - \ mathrm {{} ^ mH}) ^ +$ , um análogo do íon de uma molécula de hidrogênio $$$\ mathrm {H} _2 ^ + = (\ mathrm {He ^ -H}) ^ +$ .
Tendo examinado as diferenças entre essas duas partículas, perceberemos a eficácia do múon na redução da temperatura de ignição da fusão termonuclear.

Método LEKA MO LKAO

Portanto, temos nosso sistema molecular, composto por 2 núcleos de hidrogênio com uma carga + e (um módulo de carga de elétrons) e uma partícula (elétron ou múon) com uma carga - e . Nosso sistema, até colidir com outras partículas, é isolado e, portanto, sua energia pode ser decomposta em suas partes constituintes:

$$

$$E = T (\ mathrm {H} _1) + T (\ mathrm {H} _2) + \ underbrace {T (\ mathrm {e} ^ - / \ mu ^ -) + V (\ mathrm {H_1 \ text {from} H_2}) + V (\ mathrm {\ mathrm {e} ^ - / \ mu ^ - \ text {} \ mathrm {H} _1}) + V (\ mathrm {\ mathrm {e} ^ - / \ mu ^ - \ text {k} \ mathrm {H} _2})} _ {E_ \ mathrm {e}}$$

onde os dois primeiros termos ( $$$T (\ mathrm {H} _1)$ e $$$T (\ mathrm {H} _2)$ ) A energia cinética dos núcleos de hidrogênio, o terceiro termo ( $$$T (\ mathrm {e} ^ - / \ mu ^ -)$ ) É a energia cinética de uma partícula negativa (elétron ou múon), o quarto termo $$$V (\ mathrm {H_1 \ text {from} H_2})$ É a energia da repulsão Coulomb de hidrogênios um do outro, e os dois restantes são a atração Coulomb do elétron / múon a cada um dos prótons. No caso geral, este é um problema de três corpos, apenas um problema quântico. Naturalmente, resolvê-lo na testa é muito difícil. Felizmente, porém, os núcleos são pelo menos 1800 vezes mais pesados ​​que o elétron e 10 mais pesados ​​que o múon, de modo que eles se movem claramente mais devagar que as pequenas partículas negativas. Devido a isso, você pode primeiro resolver o problema por sua vez: primeiro, encontre a energia dos movimentos que não estão relacionados ao movimento dos núcleos, ou seja, $$$E_ \ mathrm {e}$ e então energia total. Parece assim.

1. O arranjo dos núcleos de hidrogênio em relação um ao outro é selecionado, e isso determina as interações de Coulomb entre eles e com o elétron / múon. Potencial de Coulomb $$$V (R) = k \ frac {q_1q_2} {R}$ depende apenas de cargas de partículas $$$q_i$ e a distância entre eles, portanto, para todos os isótopos de hidrogênio, esse valor será o mesmo. Além disso, o problema do movimento de um elétron / múon no campo desses núcleos é resolvido. Esta é a tarefa de um corpo.
2. Essas energias $$$E_ \ mathrm {e}$ são calculados para todos os arranjos possíveis dos núcleos em relação um ao outro, e essa será a energia potencial efetiva de movimento dos núcleos. No nosso caso, precisamos calcular as energias em distâncias diferentes entre si, para que o potencial de um par de núcleos seja sempre unidimensional. Bem, só precisamos resolver o problema de dois corpos do movimento de dois isótopos de hidrogênio um em relação ao outro.

Obviamente, a raiz do problema conosco é o cálculo da energia elétron / múon no campo dos núcleos. $$$E_ \ mathrm {e}$ . De fato, essa é a ligação química: um certo potencial que mantém os núcleos unidos em certos lugares. E essa mesma tarefa de encontrar a energia da ligação química é a principal na química quântica.

Infelizmente, tanto o múon quanto o elétron são partículas quânticas; portanto, para encontrar essa energia, precisamos recorrer aos métodos da mecânica quântica. De fato, nosso problema do movimento de um elétron / múon no campo de dois núcleos idênticos é resolvido explicitamente (veja aqui ), mas essa solução é muito complicada e o resultado não é tão claro como no caso de um átomo semelhante a hidrogênio. Portanto, tentaremos desmontar uma abordagem aproximada diferente, aplicável a qualquer sistema. Este é o chamado método de orbitais moleculares como combinações lineares de orbitais atômicos, ou MO LKAO.

Vamos dar uma olhada na equação de Schrödinger para o movimento de um elétron / múon no campo dos núcleos de hidrogênio:

$$

$$\ hat {H} \ psi = \ underbrace {\ left (\ overbrace {- \ frac {1} {2m} (\ frac {\ parcial ^ 2} {\ parcial x ^ 2} + \ frac {\ parcial ^ 2} {\ parcial y ^ 2} + \ frac {\ parcial ^ 2} {\ parcial z ^ 2})} ^ {\ hat {T}} + \ ultrapassar {- \ frac {1} {R_1}} ^ {\ hat {V} _1} + \ ultrapassar {- \ frac {1} {R_2}} ^ {\ hat {V} _2} + \ ultrapassar {\ frac {1} {R}} ^ {\ hat {V } _ \ mathrm {HH}} \ right)} _ {\ hat {H}} \ psi = E \ psi$$

Esta equação foi escrita no sistema atômico de unidades (veja PS na parte anterior ); portanto, a carga do núcleo de hidrogênio e do elétron / múon é +1, -1, respectivamente, a massa de elétrons é m = 1 e para o múon m ≈207.

E se você olhar mais de perto, poderá ver que no Hamiltoniano você pode selecionar uma peça conectada puramente ao movimento de uma partícula negativa em torno de apenas um dos núcleos, que é apenas o Hamiltoniano do átomo de hidrogênio, e isso pode ser feito de duas maneiras:

$$

$$\ hat {H} = (\ overbrace {\ hat {T} + \ hat {V} _1} ^ {\ hat {H} _ {1}} + \ hat {V} _2 + \ hat {V} _ \ mathrm {HH}) = (\ overbrace {\ hat {T} + \ hat {V} _2} ^ {\ hat {H} _ {2}} + \ hat {V} _1 + \ hat {V} _ \ mathrm {HH})$$

Fora do Hamiltoniano de um átomo do tipo hidrogênio ( $$$\ hat {H} _i, \ i = $ 1,$ ) sempre temos duas partes: a energia da interação de um elétron / múon com outro núcleo ( $$$\ hat {V} _j$ ) e energia de repulsão nuclear ( $$$\ hat {V} _ \ mathrm {HH}$ ) O segundo deles não afeta o movimento dos elétrons - é apenas uma mudança de energia em uma certa quantidade, mas a interação de um elétron com outro núcleo é uma coisa importante.
Podemos imaginar que a qualquer momento nossa partícula gira apenas em torno de um dos núcleos, e a interação com o segundo é apenas uma correção. Como método de rotação em torno de um dos núcleos, podemos assumir que o elétron / múon está no estado do solo (1s), cuja função de onda é bem conhecida da parte anterior:

$$

$$| 1s \ rangle = \ frac {1} {\ sqrt {\ pi}} \ exp \ left (- \ frac {R} {R_1} \ right)$$

onde $$$R_1$ É o raio de Bohr para uma partícula. No caso de um elétron $$$R_1 = 1$ Boro (que é o raio de Bohr para um elétron, igual a cerca de 0,5 angstroms) e, no caso de um múon $$$R_1 = \ frac {1} {m_ \ mu} \ approx \ frac {1} {207}$ .
Para aproximar de alguma forma a função de onda elétron / múon no campo de 2 núcleos, podemos tentar fazer a seguinte representação:

$$

$$\ psi \ approx c_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle$$

e então o problema de resolver uma equação diferencial parcial complexa conosco é reduzido a procurar por 2 coeficientes desconhecidos c ₁ e c ₂ . Este é o orbital muito molecular apresentado como a soma dos coeficientes (uma combinação linear dos científicos) orbitais 1s atômicos.

Naturalmente, precisamos de uma equação para esses parâmetros. E obtê-lo é bastante simples se você substituir essa aproximação na equação de Schrödinger $$$\ hat {H} \ psi = E \ psi$ :

$$

$$\ hat {H} (c_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle) = c_1 \ hat {H} | 1s_1 \ rangle + c_2 \ hat {H} | 1s_2 \ rangle = E (c_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle) = c_1 E | 1s_1 \ rangle + c_2 E | 1s_2 \ rangle$$

Na verdade, queremos que essa proporção seja satisfeita em todos os lugares, para que possamos calcular os valores médios de tudo isso. Multiplicamos esta equação à esquerda por $$$<1s_1 |$ e $$$<1s_2 |$ e integrar sobre todas as coordenadas. Como resultado, obtemos um sistema de 2 equações lineares, onde é necessário encontrar os coeficientes c ₁ , c ₂ e energia E :

$$

$$\ begin {pmatrix} \ langle 1s_1 | \ hat {H} | 1s_1 \ rangle & \ langle 1s_1 | \ hat {H} | 1s_2 \ rangle \\ \ langle 1s_2 | \ hat {H} | 1s_1 \ rangle & \ langle 1s_2 | \ hat {H} | 1s_2 \ rangle \\ \ end {pmatrix} \ begin {pmatrix} c_1 \\ c_2 \ end {pmatrix} = E \ begin {pmatrix} \ langle 1s_1 | 1s_1 \ rangle & \ langle 1s_1 | 1s_2 \ rangle \\ \ langle 1s_2 | 1s_1 \ rangle & \ langle 1s_2 | 1s_2 \ rangle \\ \ end {pmatrix} \ begin {pmatrix} c_1 \\ c_2 \ end {pmatrix}$$

Qualquer um que tenha estudado álgebra linear reconhecerá um problema generalizado de autovetor-autovalor. Antes de resolvê-lo, analisaremos a que os elementos das 2 matrizes, o tuta existente, são iguais (e ao mesmo tempo introduzimos sua designação curta com uma letra).

• Vamos começar com o mais simples: $$$\ langle 1s_1 | 1s_1 \ rangle = \ langle 1s_2 | 1s_2 \ rangle = 1$ - essa é a normalização das funções das ondas e, como lembramos, a probabilidade total de encontrar um elétron / múon é pelo menos 1 em algum lugar.
• $$$\ langle 1s_1 | 1s_2 \ rangle = \ langle 1s_2 | 1s_1 \ rangle = S$ - este é o chamado integral de sobreposição, mostrando como as nuvens de elétron 1s se sobrepõem para cada um dos átomos.
• $$$\ langle 1s_1 | \ hat {H} | 1s_1 \ rangle = \ langle 1s_2 | \ hat {H} | 1s_2 \ rangle = \ alpha$ . Essa integral consiste em várias partes:
  

  $$

  $$\ langle 1s_1 | \ hat {H} | 1s_1 \ rangle = \ underbrace {\ langle 1s_1 | \ hat {H} _1 | 1s_1 \ rangle} _ {- \ frac {m} {2}} + \ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle + \ frac {1} {R}$$
  
  
• $$$\ langle 1s_1 | \ hat {H} | 1s_2 \ rangle = \ langle 1s_2 | \ hat {H} | 1s_1 \ rangle = \ beta$ . Aqui é semelhante:
  

  $$

  $$\ langle 1s_2 | \ hat {H} | 1s_1 \ rangle = \ underbrace {\ langle 1s_2 | \ overbrace {\ hat {H} _1 | 1s_1 \ rangle} ^ {- \ frac {m} {2} | 1s_1 \ rangle}} {{\ frac {m} {2} S} + \ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle + \ frac {S} {R}$$
  
  isto é a energia de um átomo semelhante ao hidrogênio e a repulsão internuclear, dimensionada pela integral de sobreposição (primeiro e último termos) e, por assim dizer, a energia do elétron / múon pulando de um átomo para outro.
  

Vamos encontrar as expressões para as energias do nosso íon do tipo hidrogênio a partir da equação reescrita como

$$

$$\ begin {pmatrix} \ alpha & \ beta \\ \ beta & \ alpha \ end {pmatrix} \ begin {pmatrix} s_1 \\ c_2 \ end {pmatrix} = E \ begin {pmatrix} 1 e S \\ S & 1 \ end {pmatrix} \ begin {pmatrix} c_1 \\ c_2 \ end {pmatrix}$$

Para encontrar a energia que você precisa para resolver a equação:

$$

$$\ det \ begin {pmatrix} \ alpha -E & \ beta -ES \\ \ beta - ES & \ alpha -E \ end {pmatrix} = (\ alpha -E) ^ 2 - (\ beta - ES) ^ 2 = 0$$

onde "det" denota o determinante (determinante de uma matriz, em russo).

As soluções desta equação quadrática em relação a E são:

$$

$$E_ \ pm = \ frac {\ alpha \ pm \ beta} {1 \ pm S} = - \ frac {m} {2} + \ frac {1} {R} + \ frac {\ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle \ pm \ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle} {13 \ S}$$

A primeira peça é obviamente a energia do átomo, a segunda é a repulsão internuclear, a mesma barreira de Coulomb que impede a ignição da reação termonuclear e a última estrutura complexa deve ser tratada.

Se descartarmos a repulsão internuclear, que é apenas um ponto de referência para a energia elétron / múon, obtemos que temos dois estados com energia

$$

$$\ epsilon_ \ pm = - \ frac {m} {2} + \ frac {\ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle \ pm \ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle} {13h S}$$

Como as duas funções de onda $$$| 1s_1 \ rangle$ e $$$| 1s_2 \ rangle$ - positivo e $$$\ hat {V} _i <0$ (porque a partícula negativa é sempre atraída para o positivo), $$$\ epsilon_ + <- \ frac {m} {2}$ (energia de um único átomo), e $$$\ epsilon _-> - \ frac {m} {2}$ , ou seja, temos uma imagem padrão dos orbitais moleculares:



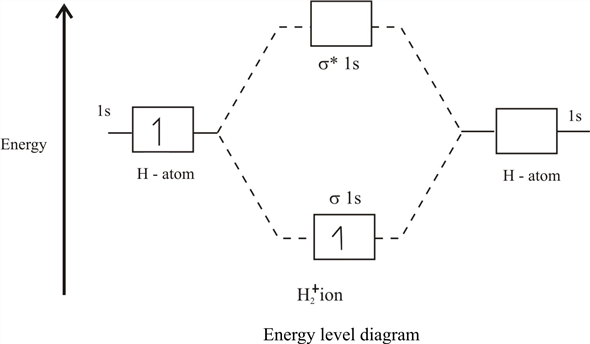
Orbital inferior com energia $$$E _ +$ chamado de encadernação e o topo (com energia $$$E _-$ ) - anti-encadernação ou afrouxamento. Como resultado, se um elétron / múon fica no orbital molecular inferior, ele se beneficia ao voar em torno de 2 núcleos que em torno de um e, com seu movimento, reduz a energia total do sistema. E essa é a ligação química muito mágica que protege a repulsão internuclear, permitindo que os núcleos fiquem próximos um do outro por algum tempo.

E aqui as integrais da ligação química devem ser calculadas para entender a proximidade com a qual os núcleos de hidrogênio podem estar. De fato, todas as três integrais procuradas são calculadas analiticamente, mas são terrivelmente hemorróidas e complicadas (qualquer pessoa interessada, consulte o Capítulo 9 no livro de Química Quântica de Flary ). Portanto, seguiremos um caminho diferente, mais simples e calcularemos essas integrais numericamente usando o método Monte Carlo.

Método Metropolis

Eu vejo como muito lógico no texto sobre energia termonuclear prestar homenagem ao seu avô: o átomo militar e, mais especificamente, o projeto de Manhattan . Foi a partir dele que o método Monte Carlo cresceu, e em particular o algoritmo Metropolis , um dos autores, Edward Teller, é o "pai da bomba de hidrogênio" (ou seja, a pessoa que lançou a fusão termonuclear no Atol Envetok).


Em geral, analisaremos a essência do método. Destina-se às tarefas da mecânica estatística. A principal distribuição é a distribuição de Boltzmann: a probabilidade de detectar um sistema em um determinado estado é $$$\ exp (- \ beta E)$ , $$$\ beta ^ {- 1} = k_ \ mathrm {B} T$ . E o valor observado de algum parâmetro A para o sistema em equilíbrio termodinâmico é igual à integral

$$

$$\ langle A \ rangle = \ frac {1} {Z} \ int A (q) \ exp (- \ beta E (q)) dq$$

onde q são as coordenadas que parametrizam o estado do sistema (por exemplo, as coordenadas / momento das partículas) e Z é o fator de normalização chamado função de partição:

$$

$$Z = \ int \ exp (- \ beta E (q)) dq$$

Se houver muuuitas partículas no sistema, a contagem de nenhuma das integrais na testa é completamente irrealista. O ingênuo método de Monte Carlo, no qual simplesmente selecionamos um monte de coordenadas q aleatórias, também não dará nada significativo se houver realmente estados possíveis do sistema para os quais a probabilidade $$$\ exp (- \ beta E)$ visivelmente diferente de zero, muito poucos. E é justamente nesses casos que precisamos de uma amostra por significância, na qual permitimos que o algoritmo prove apenas locais suficientemente prováveis ​​no espaço de estados.

O algoritmo Metropolis tem a seguinte aparência.

1. Ao iniciar a simulação, selecionamos algumas aproximações iniciais no espaço de configuração $$$\ mathbf {q} ^ {(0)}$ e algum vetor do incremento máximo possível $$$\ delta \ mathbf {q}$ . No ponto de partida, calculamos a energia do sistema $$$E ^ {(0)} = E (\ mathbf {q} ^ {(0)})$ (leitura - probabilidade $$$p = \ exp (- \ beta E ^ {(0)})$ )
2. A nova configuração na enésima etapa é a seguinte.
   
   1. Calcular a energia da configuração de avaliação $$$E_ \ mathrm {trial} = E (\ mathbf {q} _ \ mathrm {trial})$ (ou seja, probabilidade $$$p_ \ mathrm {trial} = \ exp (- \ beta E_ \ mathrm {trial})$ )
   2. E então comparamos a velha probabilidade $$$p ^ {(n)}$ com julgamento $$$p_ \ mathrm {trial}$
      
      
      • se a nova configuração tiver uma probabilidade maior ou igual ( $$$\ frac {p_ \ mathrm {trial}} {p ^ {(n)}} \ geq 1$ ) ou, equivalente, a energia do novo ponto é menor ou igual à do antigo ( $$$E_ \ mathrm {trial} \ leq E ^ {(n)}$ ), o novo ponto é aceito e o sistema entra nele ( $$$q ^ {(n + 1)} = q_ \ mathrm {avaliação}$ ),
      • se a configuração de teste for mais alta em energia ( $$$E_ \ mathrm {trial}> E ^ {(n)}$ ), que é equivalente $$$\ frac {p_ \ mathrm {trial}} {p ^ {(n)}} <1$ , nesse caso, geramos um número aleatório $$$P \ em [0; 1)$ de uma distribuição uniforme e compare-a com a razão de probabilidades, que são as probabilidades de transição. Se $$$P <\ frac {p_ \ mathrm {trial}} {p ^ {(n)}}$ , aceitamos um novo ponto e, se não ( $$$P \ geq \ frac {p_ \ mathrm {trial}} {p ^ {(n)}}$ ), rejeitamos e o sistema permanece na configuração antiga ( $$$q ^ {(n + 1)} = q ^ {(n)}$ ) ...
      
      
   
   
3. Dando muitas etapas de acordo com o algoritmo acima, amostramos uma parte significativa (isto é, realmente importante) do espaço possível das configurações do sistema. A integral de interesse para nós é calculada pela fórmula:
   $$$\ langle A \ rangle = \ frac {1} {Z} \ int A (\ mathbf {q}) \ exp (- \ beta E (\ mathbf {q})) d \ mathbf {q} = \ frac { 1} {N} \ sum_ {n = 0} ^ {N} A (\ mathbf {q} ^ {(n)})$
   

É assim que o algoritmo Metropolis funciona.

E agora seria necessário adaptá-lo ao cálculo das 3 integrais que nos interessam. Vamos olhar para eles com mais detalhes.

• $$$S (R) = \ langle 1s_2 | 1s_1 \ rangle = \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-m \ underbrace {| \ mathbf {r} - \ mathbf {r} _2 | } _ {R_2})} _ {1s_2}} ^ {A (\ mathbf {r})} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-m \ subjacente {| \ mathbf {r} - \ mathbf {r} _1 |} _ {R_1})} _ {1s_1}} ^ {p (\ mathbf {r})} dx dy dz$ onde $$$\ mathbf {r} = (x, y, z) ^ \ mathbf {T}$ - coordenadas do elétron / múon, $$$\ mathbf {r} _i = (x_i, y_i, z_i) ^ \ mathbf {T}$ As coordenadas dos núcleos de hidrogênio e $$$R_i = | \ mathbf {r} - \ mathbf {r} _i | = \ sqrt {(x-x_i) ^ 2 + (y-y_i) ^ 2 + (z-z_i) ^ 2}$ - distâncias entre partículas positivas e negativas,
  
• $$$\ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle = - \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limites _ {- \ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_1)} _ {1s_1} \ frac {1} {R_2} } ^ {A (\ mathbf {r})} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_1)} _ {1s_1}} ^ {p (\ mathbf {r})} dxdydz$
• $$$\ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle = - \ int \ limit _ {- \ infty} ^ {+ \ infty} \ int \ limit _ {- \ infty} ^ {+ \ infty} \ int \ limites _ {- \ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_2)} _ {1s_2} \ frac {1} {R_1} } ^ {A (\ mathbf {r})} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_1)} _ {1s_1}} ^ {p (\ mathbf {r})} dxdydz$

Vê-se que, se calcularmos a função 1s de um dos átomos para a probabilidade p ,


então tudo o mais sob o signo da integral (a função de segunda onda e em 2 de 3 casos o potencial de atração do elétron / múon para o núcleo) será uma função cujo valor médio é calculado. A única coisa que terá que ser feita, em contraste com o cálculo usual pelo método Metropolis, é endireitar a normalização das integrais. O fato é que a normalização padrão estará em

$$

$$Z = \ int \ limit _ {- \ infty} ^ {+ \ infty} \ int \ limit _ {- \ infty} ^ {+ \ infty} \ int \ limit _ {- \ infty} ^ {+ \ infty} \ exp (-m R) dx dy dz = 4 \ pi \ int \ limits_ {0} ^ {+ \ infty} \ exp (-m R) R ^ 2 dR = \ frac {8 \ pi} {m ^ 3}$$

E precisamos de normalização para $$$\ sqrt {\ langle 1s_1 | 1s_1 \ rangle}$ onde

$$

$$\ langle 1s_1 | 1s_1 \ rangle = \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limit _ {- \ infty} ^ {+ \ infty} \ exp (-2 m R) dx dy dz = 4 \ pi \ int \ limits_ {0} ^ {+ \ infty} \ exp (-2m R) R ^ 2 dR = \ frac {\ pi} {m ^ 3}$$

Isso significa que cada integral calculado de acordo com a metrópole precisará ser multiplicado por um fator

$$

$$\ frac {Z} {\ sqrt {\ langle 1s_1 | 1s_1 \ rangle}} = 8 \ sqrt {\ frac {\ pi} {m ^ 3}}$$

Isso já pode ser organizado na forma de um determinado script, por exemplo, em Python (por exemplo, o código está abaixo).


Usando esses cálculos, podemos finalmente comparar as energias potenciais no íon hidrogênio $$$\ mathrm {H} _2 ^ +$ e sua contraparte múon.

$$$\ mathrm {H_2 ^ + = p ^ + e ^ - p ^ +}$ vs. $$$\ mathrm {p ^ + \ mu ^ - p ^ +}$

Assim, armados com um script, podemos calcular a superfície da energia potencial da abordagem dos núcleos de hidrogênio ligados por um elétron e um múon. Como ponto de referência de energia, tomamos átomos infinitamente diluídos um do outro (ou seja, $$$-m / 2$ , que é igual ao potencial à distância entre os núcleos $$$R = + \ infty$ )

No caso de um elétron, o potencial próximo ao mínimo se parece com o seguinte:



O mínimo ocorre a uma distância de cerca de 2 boro (isto é, aproximadamente a soma de 2 raios atômicos) e a energia de dissociação da molécula em fragmentos é de aproximadamente 0,06 Hartree, o que corresponde ao aquecimento a cerca de 20.000 graus Kelvin (ou Celsius, isso não importa aqui). Para converter energias, recomendo o uso de recursos online, como este .

Uma situação semelhante com um íon de hidrogênio ligado muonalmente:



Como o raio de Bohr para o hidrogênio do múon é menor (veja a parte anterior ), os núcleos de hidrogênio também ficam 200 vezes mais próximos da energia potencial mínima. A energia de decomposição desta molécula já é superior a 10 Hartree, o que corresponde a uma temperatura superior a três graus lyam ( $$$\ approx (3,2 \ cdot 10 ^ 6) ^ \ circ$ )

Para a ignição, as reações geralmente requerem uma temperatura da ordem de 10 ⁸ K , que é de cerca de 320 Hartree. Vamos ver a que distâncias uma energia semelhante é alcançada no caso do íon de desodorização comum e no caso de sua versão de múon:



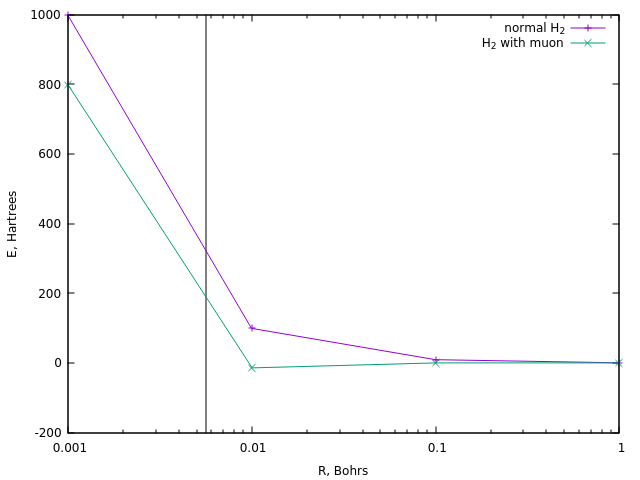
No primeiro caso, isso corresponde a uma distância de cerca de 0,0058 boro (linha vertical).

Uma distância semelhante no hidrogênio do múon é alcançada a uma energia de cerca de 190 Ha, isto é, cerca de uma vez e meia menos. E esta é a estimativa mais simples da temperatura da catálise do múon.

Mas, de fato, tudo será ainda mais legal. O fato é que, se uma partícula estável é formada $$$\ mathrm {({} ^ mH (\ mu ^ -) {} ^ nH) ^ +}$ , então esses núcleos, enquanto o múon estiver vivo, oscilarão um em relação ao outro. E aqui o tunelamento do estado "dois átomos de hidrogênio" para o estado "núcleo mais pesado" pode ocorrer, e a probabilidade de tunelamento depende do comprimento de tunelamento necessário d aproximadamente como $$$p ^ {- d}$ , de modo que, aproximando os dois núcleos pelo múon, aumentaremos bastante a probabilidade do curso de tunelamento dessa reação. Infelizmente, as estimativas desse efeito não exigem mais química quântica, mas física nuclear, portanto essa parte da discussão está além do escopo deste post. Então, sobre isso, vamos parar.

PS Por que não é tão simples?

De fato, formar essas partículas não é tão simples em condições de plasma. O fato é que, se colidirmos duas partículas, sua energia total obviamente excederá a energia de dissociação (ou ionização, no caso de um núcleo + elétron / múon); portanto, quando colidem, elas não formam uma partícula estável (átomo, íon, molécula), mas voam passado um do outro. Para se manterem firmes, eles precisam desperdiçar energia excedente em algum lugar e, para isso, precisamos de um terceiro extra que absorve essa energia. Pode ser um fóton, ou algum tipo de partícula esquerda voando por perto, mas o principal é que as condições contribuam para esse arrastamento do excesso de energia.

PPS

Se você tiver quaisquer comentários / esclarecimentos / perguntas, escreva nos comentários ou no PM. Vou corrigir tudo, vou responder e explicar tudo.