Entrada
No
YOW! 2013 um dos desenvolvedores da linguagem Haskell,
prof. Philip Wadler mostrou como as mônadas permitem que linguagens funcionais puras realizem operações essencialmente imperativas, como manipulação de entrada e saída e exceção. Não é de surpreender que o interesse do público neste tópico tenha gerado um crescimento explosivo em publicações sobre mônadas na Internet. Infelizmente, a maioria dessas publicações usa exemplos escritos em linguagens funcionais, o que implica que os novatos em programação funcional desejam aprender sobre mônadas. Mas as mônadas não são específicas para Haskell ou linguagens funcionais e podem muito bem ser ilustradas por exemplos em linguagens de programação imperativas. Este é o objetivo deste guia.
Qual é a diferença deste guia para o resto? Vamos tentar abrir as mônadas em não mais de 15 minutos usando apenas intuição e alguns exemplos elementares de código Python. Portanto, não começaremos a teorizar e aprofundar a filosofia, discutindo
burritos ,
trajes espaciais ,
mesas e endofuncionadores.
Exemplos motivacionais
Vamos considerar três questões relacionadas à composição de funções. Vamos resolvê-los de duas maneiras: o imperativo usual e o uso de mônadas. Depois, comparamos as diferentes abordagens.
1. Registro
Suponha que temos três funções unárias:
f1 ,
f2 e
f3 , que recebem um número e o retornam aumentado em 1, 2 e 3, respectivamente. Cada função também gera uma mensagem, que é um relatório sobre a operação concluída.
def f1(x): return (x + 1, str(x) + "+1") def f2(x): return (x + 2, str(x) + "+2") def f3(x): return (x + 3, str(x) + "+3")
Gostaríamos de encadeá-los para processar o parâmetro
x , ou seja, gostaríamos de calcular
x+1+2+3 . Além disso, precisamos obter uma explicação legível por humanos do que cada função fez.
Podemos alcançar o resultado que precisamos da seguinte maneira:
log = "Ops:" res, log1 = f1(x) log += log1 + ";" res, log2 = f2(res) log += log2 + ";" res, log3 = f3(res) log += log3 + ";" print(res, log)
Esta solução não é ideal, pois consiste em um grande número de middleware monótono. Se quisermos adicionar uma nova função à nossa cadeia, seremos forçados a repetir esse código de ligação. Além disso, manipulações com as variáveis
res e
log prejudicam a legibilidade do código, dificultando o monitoramento da lógica do programa principal.
Idealmente, um programa deve parecer uma cadeia simples de funções, como
f3(f2(f1(x))) . Infelizmente, os tipos de dados retornados por
f1 e
f2 não correspondem aos tipos de parâmetro
f2 e
f3 . Mas podemos adicionar novas funções à cadeia:
def unit(x): return (x, "Ops:") def bind(t, f): res = f(t[0]) return (res[0], t[1] + res[1] + ";")
Agora podemos resolver o problema da seguinte maneira:
print(bind(bind(bind(unit(x), f1), f2), f3))
O diagrama a seguir mostra o processo computacional que ocorre em
x=0 . Aqui
v1 ,
v2 e
v3 são os valores obtidos como resultado de chamadas para
unit e
bind .

A função da
unit converte o parâmetro de entrada
x em uma tupla de um número e uma string. A função de
bind chama a função passada para ele como um parâmetro e acumula o resultado na variável intermediária
t .
Conseguimos evitar a repetição do middleware colocando-o na função de
bind . Agora, se
f4 a função
f4 , apenas a incluiremos na cadeia:
bind(f4, bind(f3, ... ))
E não precisamos fazer outras alterações.
2. Lista de valores intermediários
Também iniciaremos este exemplo com funções unárias simples.
def f1(x): return x + 1 def f2(x): return x + 2 def f3(x): return x + 3
Como no exemplo anterior, precisamos compor essas funções para calcular
x+1+2+3 . Também precisamos obter uma lista de todos os valores obtidos como resultado do trabalho de nossas funções, ou seja,
x ,
x+1 ,
x+1+2 x+1+2+3 .
Diferentemente do exemplo anterior, nossas funções são compostas, ou seja, os tipos de seus parâmetros de entrada coincidem com o tipo do resultado. Portanto, uma cadeia simples
f3(f2(f1(x))) retornará o resultado final. Mas, neste caso, perdemos os valores intermediários.
Vamos resolver o problema "de frente":
lst = [x] res = f1(x) lst.append(res) res = f2(res) lst.append(res) res = f3(res) lst.append(res) print(res, lst)
Infelizmente, esta solução também contém muitos middlewares. E se decidirmos adicionar
f4 , teremos que repetir esse código novamente para obter a lista correta de valores intermediários.
Portanto, adicionamos duas funções adicionais, como no exemplo anterior:
def unit(x): return (x, [x]) def bind(t, f): res = f(t[0]) return (res, t[1] + [res])
Agora reescrevemos o programa como uma cadeia de chamadas:
print(bind(bind(bind(unit(x), f1), f2), f3))
O diagrama a seguir mostra o processo computacional que ocorre em
x=0 . Novamente,
v1 ,
v2 e
v3 denotam os valores obtidos da
unit e das chamadas de
bind .

3. Valores vazios
Vamos tentar dar um exemplo mais interessante, desta vez com classes e objetos. Suponha que tenhamos uma classe
Employee com dois métodos:
class Employee: def get_boss(self):
Cada objeto da classe
Employee possui um gerente (outro objeto da classe
Employee ) e um salário, que são acessados por métodos apropriados. Ambos os métodos também podem retornar
None (o funcionário não tem um gerente, o salário é desconhecido).
Neste exemplo, criaremos um programa que mostra o salário do líder desse funcionário. Se o gerente não for encontrado ou seu salário não puder ser determinado, o programa retornará
None .
Idealmente, precisamos escrever algo como
print(john.get_boss().get_wage())
Mas, neste caso, se algum dos métodos retornar
None , nosso programa terminará com um erro.
Uma maneira óbvia de lidar com essa situação pode ser assim:
result = None if john is not None and john.get_boss() is not None and john.get_boss().get_wage() is not None: result = john.get_boss().get_wage() print(result)
Nesse caso, permitimos chamadas extras para os
get_wage e
get_wage . Se esses métodos forem pesados o suficiente (por exemplo, acessar o banco de dados), nossa solução não funcionará. Portanto, nós mudamos:
result = None if john is not None: boss = john.get_boss() if boss is not None: wage = boss.get_wage() if wage is not None: result = wage print(result)
Esse código é ideal em termos de cálculo, mas é mal lido devido a três
if aninhados. Portanto, tentaremos usar o mesmo truque dos exemplos anteriores. Defina duas funções:
def unit(e): return e def bind(e, f): return None if e is None else f(e)
E agora podemos colocar toda a solução em uma linha.
print(bind(bind(unit(john), Employee.get_boss), Employee.get_wage))
Como você provavelmente já percebeu, neste caso, não precisamos escrever a função da
unit : ela simplesmente retorna o parâmetro de entrada. Mas deixaremos para que seja mais fácil para nós generalizar nossa experiência.
Observe também que no Python podemos usar métodos como funções, o que nos permitiu escrever
Employee.get_boss(john) vez de
john.get_boss() .
O diagrama a seguir mostra o processo de cálculo quando John não possui um líder, ou seja,
john.get_boss() retorna
None .
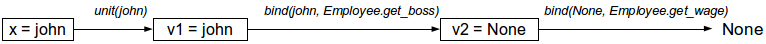
Conclusões
Suponha que desejemos combinar as funções do mesmo tipo
f1 ,
f2 ,
… ,
fn . Se seus parâmetros de entrada forem os mesmos que os resultados, podemos usar uma cadeia simples do formato
fn(… f2(f1(x)) …) . O diagrama a seguir mostra um processo de cálculo generalizado com resultados intermediários, indicado como
v1 ,
v2 ,
… ,
vn .

Muitas vezes, essa abordagem não é aplicável. Os tipos de valores de entrada e resultados da função podem variar, como no primeiro exemplo. Ou as funções podem ser compostas, mas queremos inserir lógica adicional entre as chamadas, pois nos exemplos 2 e 3 inserimos uma agregação de valores intermediários e uma verificação de um valor vazio, respectivamente.
1. Decisão imperativa
Em todos os exemplos, primeiro usamos a abordagem mais direta, que pode ser representada pelo seguinte diagrama:

Antes de chamar
f1 fizemos algumas inicializações. No primeiro exemplo, inicializamos uma variável para armazenar um log comum, no segundo, para uma lista de valores intermediários. Depois disso, intercalamos as chamadas de função com um determinado código de conexão: calculamos valores agregados, verificamos o resultado como
None .
2. Mônadas
Como vimos nos exemplos, as decisões imperativas sempre sofriam de verbosidade, repetição e lógica confusa. Para obter um código mais elegante, usamos um certo padrão de design, segundo o qual criamos duas funções:
unit e
bind . Este modelo é chamado de
mônada . A função de
bind contém middleware enquanto a
unit implementa a inicialização. Isso nos permite simplificar a solução final para uma linha:
bind(bind( ... bind(bind(unit(x), f1), f2) ... fn-1), fn)
O processo de cálculo pode ser representado por um diagrama:

Uma chamada para a
unit(x) gera um valor inicial de
v1 . Em seguida,
bind(v1, f1) gera um novo valor intermediário
v2 , que é usado na próxima chamada para
bind(v2, f2) . Esse processo continua até que um resultado final seja obtido. Ao definir várias
unit e
bind -se à estrutura deste modelo, podemos combinar várias funções em uma cadeia de cálculos. Bibliotecas
de mônadas (
por exemplo, PyMonad ou OSlash - aprox. Transl. ) Geralmente contêm mônadas prontas para uso (pares de
unit e funções de
bind ) para implementar determinadas composições de funções.
Para encadear funções, os valores retornados por
unit e
bind devem ser do mesmo tipo que os parâmetros de entrada de
bind . Este tipo é chamado
monádico . Nos termos do diagrama acima, o tipo de variáveis
v1 ,
v2 ,
… ,
vn deve ser do tipo monádico.
Por fim, considere como você pode melhorar o código escrito usando mônadas. Obviamente, chamadas de
bind repetidas parecem deselegantes. Para evitar isso, defina outra função externa:
def pipeline(e, *functions): for f in functions: e = bind(e, f) return e
Agora em vez
bind(bind(bind(bind(unit(x), f1), f2), f3), f4)
podemos usar a seguinte abreviação:
pipeline(unit(x), f1, f2, f3, f4)
Conclusão
Mônadas são um padrão de design simples e poderoso usado para compor funções. Em linguagens de programação declarativa, ajuda a implementar mecanismos imperativos, como registro em log ou entrada / saída. Em línguas imperativas
ajuda a generalizar e reduzir o código que vincula uma série de chamadas de funções do mesmo tipo.
Este artigo fornece apenas uma compreensão superficial e intuitiva das mônadas. Você pode descobrir mais entrando em contato com as seguintes fontes:
- Wikipedia
- Mônadas em Python (com boa sintaxe!)
- Linha do tempo dos tutoriais da Mônada