Tipos de infinitos e tronco cerebral

Este artigo é uma continuação de um artigo sobre grandes números . Mas agora iremos ainda mais longe - no infinito do infinito.

Para isso, precisamos do ZFC - a teoria dos conjuntos Zermelo, Frenkel + Choice. A escolha é o axioma da escolha, o axioma mais controverso da teoria dos conjuntos. Ela merece um artigo separado. Supõe-se que você saiba qual é o "poder" do aparelho. Se não, então google, com certeza isso é afirmado melhor do que eu posso. Aqui vou lembrar apenas alguns

Fatos conhecidos

• A potência de um conjunto de números inteiros é denotada por $$ . Este é o primeiro poder infinito; esses conjuntos são chamados contáveis.
• O poder de qualquer subconjunto infinito de números inteiros é simples, uniforme etc. - também contável.
• O conjunto de números racionais, isto é, as frações p / q, também é contável; eles podem ser passados ​​por uma cobra.
• Para qualquer poder, há uma operação de conjunto de energia - o conjunto de todos os subconjuntos que cria mais energia que o original. Às vezes, essa operação é referida como aumentar dois para uma potência, ou seja, $$ . O conjunto de potência da potência calculada é a potência do continuum.
• A potência contínua é possuída por: segmentos finitos e infinitos, figuras planas e volumétricas e até espaços n-dimensionais como um todo
• Para matemática comum, o seguinte poder, $$ praticamente não é necessário, geralmente todo o trabalho acontece com conjuntos contáveis ​​e conjuntos de potência contínua

Agora

Fatos pouco conhecidos

No ZFC, nem todas as coleções de elementos podem ser conjuntos. Existem coleções tão amplas que é impossível permitir que sejam conjuntos; paradoxos surgem. Em particular, o " conjunto de todos os conjuntos " não é um conjunto. No entanto, existem teorias de conjuntos em que esses conjuntos são permitidos.

Mais longe. Teoria dos Conjuntos ... Que Objetos? Números? Uma maça? Laranjas? Curiosamente, o ZFC não precisa de nenhum objeto. Pegue o conjunto vazio {} e concorde que isso significa 0. 1 denotado por {{}} o empate como {{{}}} e assim por diante. {5,2} é {{{{{{}}}}}}, {{{}}}}. Usando números inteiros, podemos criar reais, e coleções de reais podem criar qualquer forma.

Então a teoria dos conjuntos é ... como dizer ... a teoria oca. Esta teoria é sobre nada. Mais precisamente, sobre como você pode aninhar (aninhar, ou seja, colocar um no outro) chaves.

A única operação definida na teoria dos conjuntos é $$ - um símbolo de pertença. Mas e a unificação, exclusão, igualdade, etc.? Estas são todas as macros, por exemplo:

$$

Ou seja, na tradução para o russo, dois conjuntos são considerados iguais quando, ao testar qualquer elemento que pertença a eles, obteremos os mesmos resultados

Os conjuntos não são ordenados, mas isso pode ser corrigido: deixe o par ordenado (p, v) ser {{p}, {p, v}}. Deselegante do ponto de vista do programador, mas o suficiente para um matemático. Agora, o conjunto de todos os pares de valores param define uma função, que agora também é definida! Et voila! toda análise matemática, que funciona no nível das linguagens de segunda ordem , já que fala não da existência de números , mas da existência de funções , entra em colapso em uma linguagem de primeira ordem!

Assim, a teoria dos conjuntos é uma teoria pobre, sem objetos e com um ícone de relação, que tem poder absolutamente monstruoso - sem novas suposições, gera por si mesma aritmética formal, números reais, análise, geometria e muito mais. Este é um tipo de matemática TOE.

Hipótese de Continuum - CH

Existe energia entre $$ e $$ ? Cantor não conseguiu resolver esse problema: o “rei dos matemáticos” Hilbert elogiou sua importância, mas somente mais tarde ficou provado que essa hipótese não pode ser provada nem refutada. Ela é independente da ZFC.

Isso significa que você pode criar duas matemáticas diferentes: uma com ZFC + CH e outra com ZFC + (não CH). De fato, ainda mais que dois. Suponha que rejeitemos o CH, ou seja, acreditaremos que entre $$ e $$ ainda há poder. Quantos podem existir? Um dois? Godel acreditava que apenas um. Mas, como se viu, a suposição de que existem 2, 17, 19393493 deles não leva a contradições. Qualquer número, mas não infinito!

Quando na aritmética formal nos deparamos com uma afirmação improvável, por certas razões, sabemos que, no entanto, essa afirmação, embora não seja comprovável, é realmente verdadeira ou falsa. Na teoria dos conjuntos, isso não funciona, temos realmente matemáticos diferentes. Como se relacionar com isso? Existem três abordagens filosóficas:

Formalismo: por que, de fato, se surpreender? Estabelecemos as regras do jogo dos símbolos, regras diferentes - um resultado diferente. Não há necessidade de procurar um problema onde ele não existe

Platonismo: Mas como explicar que teorias completamente diferentes, como ZFC e Novas Fundações, construídas com princípios completamente diferentes, quase sempre dão o mesmo resultado? Isso significa que, por trás das fórmulas, existe algum tipo de realidade que estamos estudando? Essa opinião foi defendida, por exemplo, por Godel

Multiverso: podemos ter muitos axiomatics, às vezes dando o mesmo resultado, às vezes não. Precisamos perceber a imagem como um todo - se a cor está associada a diferentes sistemas de axiomas, a árvore de efeitos colorida é a matemática. Se algo é verdade em todos os lugares - é branco, mas também existem galhos coloridos.

Mais e mais.

No futuro, por simplicidade, aceitaremos a hipótese do continuum, ou seja, $$ - é muito conveniente. De fato, também aceitaremos o axioma mais forte, a hipótese do continuum generalizado de que entre x e powerset (x) nunca existem potências intermediárias. Agora, iteramos o conjunto de energia e tudo é simples:

$$

Até onde podemos ir? Após um número infinito de iterações, chegamos a $$ - poder infinito em ordem! A propósito, sua existência não era óbvia para Cantor. Mas um segundo! Afinal, a função powerset é sempre definida, portanto, $$ não pode ser o último!

$$

Para obter $$ é necessário repetir o infinito do conjunto de potências e mais três vezes . Você já começou a demolir o telhado? Ou então será. Porque, novamente, tendo iterado powerset um número infinito de vezes, chegamos a $$ , após o que, naturalmente, $$

Tendo atingido o infinito um número infinito de vezes , obtemos o índice $$ . Como você gosta desse poder, por exemplo: $$ ? Enquanto iteramos o powerset sobre a lista de ordinais, aqui estão os ordinais iniciais:



mas há muitos, muitos mais. Então, vamos pular tudo imediatamente e fazê-lo

Grande passo imediatamente

Atenção! O que está escrito abaixo pode ser perigoso para o seu cérebro! Nós iteramos o conjunto de potências um número contável de vezes, mas não acenamos para o continuum ? Honestamente, eu próprio sou um pouco salsicha do fato de que o ciclo pode ser realizado um continuum de tempos, mas a teoria dos conjuntos requer existência

$$

Em seguida, iremos mais rápido:

$$

O último Alef tem um índice zero, mas o látex local não permite que ele seja colocado - há muitos níveis. Mas o principal é que você entendeu, não importa quão novo poder monstruoso nós criaríamos, podemos dizer - sim, isso é apenas um repetidor e colocar toda essa construção na forma de um índice para o novo Aleph. Agora as capacidades estão crescendo como uma bola de neve, não podemos parar, a pirâmide de Alephs é maior e podemos criar qualquer poder ... Ou não?

Potência inacessível

E se houver um poder tão grande $$ que, por mais que tentemos alcançá-lo “de baixo”, construindo estruturas de Alephs, não o conseguiremos? Acontece que a existência de tal poder é independente da ZFC. Você pode aceitar sua existência ou não.

Eu ouço o sussurro da navalha de Occam ... Não, não. Os matemáticos aderem ao princípio oposto, chamado maximalismo ontológico - deixe existir tudo o que é possível. Mas há pelo menos mais duas razões pelas quais eu quero aceitar essa hipótese.

• Em primeiro lugar, este não é o primeiro poder inatingível que conhecemos. Primeiro ... este é o poder de contagem familiar. Curiosamente, ele tem todas as propriedades inatingíveis - não é habitual chamá-lo assim:
• Não há como obter energia infinita "de baixo" - nem adicionando elementos um número finito de vezes, nem iterando o conjunto de poderes () um número finito de vezes, usando conjuntos finitos para semeadura, você não obterá o infinito. Para obter o infinito, você já deve tê-lo em algum lugar.
• A existência de poder infinito é introduzida por um axioma especial - o axioma do infinito. Sem ele, a existência de poder infinito é improvável.

Segundo: se rejeitarmos o axioma do infinito, obtemos o FinSet, uma teoria simples de conjuntos de brinquedos com conjuntos finitos. Vamos escrever todos esses conjuntos (o chamado modelo de teoria )

{}
{{}}
{{{}}, {}}
{{{{}}}}
{{{{}}}, {{}}}
{{{{}}}, {{}}}
{{{{}}}, {{}}, {}}
...

E temos ... um conjunto infinito de conjuntos finitos ... Ou seja, o modelo da teoria dos conjuntos finitos é infinito e desempenha o papel de "o conjunto de todos os conjuntos" nele. Talvez isso ajude a entender por que a teoria não pode falar sobre o "conjunto de todos os conjuntos" - esse conjunto sempre existe como modelo fora da teoria e tem outras propriedades além dos conjuntos dentro. Você não pode adicionar o infinito à teoria dos conjuntos finitos.

E sim $$ é a "multidão de todas as multidões" da teoria da ZFC. Neste vídeo, no final, é muito bem dito sobre poder inatingível, mas temos que continuar.

Ainda mais.

Claro, podemos ir mais longe repetindo $$ . Depois de passar por todas as etapas descritas acima, construindo enormes torres repetidoras, encontramos novamente um cardeal inatingível (mas agora não precisamos de novos axiomas, com o axioma da existência de poder inatingível que acabamos de adicionar, isso se tornou comprovável). E de novo e de novo.

$$

Observe que agora a seta não faz sentido para nós, como executar a função Powerset (), mas GetNextInaccessible (). Caso contrário, tudo parece muito semelhante, temos:

$$

Agora, definitivamente, conseguiremos alguma coisa ... Ou não?

Hierarquia de grandes capacidades.

Sim, com GetNextInaccessible, encontramos um poder hiperatravável. Sua existência requer mais um axioma. Existem poderes hiper-hiper-inacessíveis. E assim por diante Mas existem outras maneiras de determinar o poder , não apenas pela inatingibilidade:



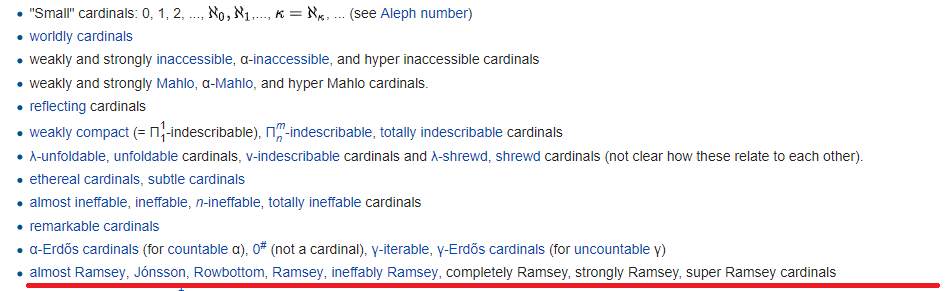
Por trás de cada link há, regra geral, uma hierarquia infinita com um número arbitrário de prefixos de hiper e repetidores. No entanto, o número total de fórmulas que determinam cardeais inatingíveis não é tão grande - porque o número de fórmulas é contável !!! Portanto, mais cedo ou mais tarde eles terminarão. Onde eles terminam, uma linha vermelha é desenhada. Tudo abaixo dessa linha é definido de maneira mais instável, embora formalmente.

A própria linha vermelha marca o fim do universo de Gödel (mas não esqueça que Gödel criou DOIS universos diferentes) - o universo de conjuntos construídos a partir de baixo usando fórmulas. As capacidades acima da linha vermelha são chamadas hmm, "pequenas" e abaixo - grandes:



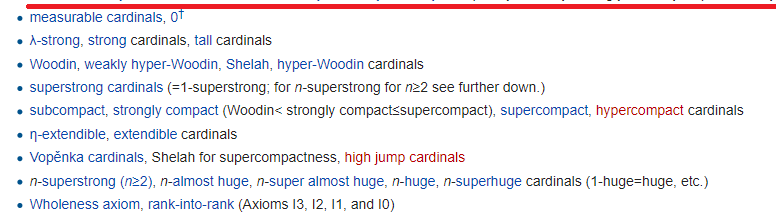
A idéia principal neles é que o universo dos conjuntos se torna tão grande que começa a se repetir em sentidos diferentes. Cada linha, como sempre, requer um axioma separado, e vários. E, mais interessante, tudo isso não é tão inútil quanto você imagina. Por exemplo, o axioma mais forte (classificação em classificação), na linha de fundo, é necessário para provar o fato sobre os tablets .

Abaixo está uma pesquisa, a última opção é descriptografada aqui .