Não, bem, é claro, não estou falando sério. Deve haver um limite até que ponto é possível simplificar o assunto. Mas para os primeiros estágios, uma compreensão dos conceitos básicos e uma rápida "entrada" no tópico, isso pode ser permitido. E como nomear adequadamente esse material (opções: “Aprendizado de máquina para manequins”, “Análise de dados das fraldas”, “Algoritmos para os menores”), discutiremos no final.
Para negócios. Ele escreveu vários programas aplicativos no MS Excel para visualização e visualização de processos que ocorrem em diferentes métodos de aprendizado de máquina ao analisar dados. Ver é acreditar, no final, de acordo com a mídia da cultura que desenvolveu a maioria desses métodos (a propósito, de modo algum todos. O mais poderoso "método de vetor de suporte", ou SVM, máquina de vetores de suporte é uma invenção de nosso compatriota Vladimir Vapnik, Instituto de Gerenciamento de Moscou. A propósito, em 1963, agora ele ensina e trabalha nos EUA).
Três arquivos para revisão
1. Cluster K-significa
Tarefas desse tipo estão relacionadas ao "aprendizado sem professor", quando precisamos dividir os dados iniciais em um certo número de categorias conhecidas antecipadamente, mas não temos um número suficiente de "respostas corretas", precisamos extraí-los dos próprios dados. O problema clássico fundamental de encontrar subespécies de flores de íris (Ronald Fisher, 1936!), Considerado o primeiro sinal desse campo de conhecimento - é dessa natureza.
O método é bastante simples. Temos um conjunto de objetos representados como vetores (conjuntos de N números). Para íris, são conjuntos de 4 números que caracterizam uma flor: o comprimento e a largura dos lobos perianto externo e interno, respectivamente (
Iris Fisher - Wikipedia ). Como distância ou medida da proximidade entre os objetos, é escolhida a métrica cartesiana usual.
Além disso, os centros dos clusters são selecionados arbitrariamente (ou não arbitrariamente, veja abaixo) e as distâncias de cada objeto aos centros dos clusters são calculadas. Cada objeto nesta etapa de iteração é marcado como pertencente ao centro mais próximo. Em seguida, o centro de cada aglomerado é transferido para a média aritmética das coordenadas de seus membros (por analogia com a física, também é chamado de "centro de massa"), e o procedimento é repetido.
O processo converge com rapidez suficiente. Nas imagens em bidimensionalidade, fica assim:
1. A distribuição aleatória inicial de pontos no avião e o número de aglomerados

2. Definindo os centros de clusters e atribuindo pontos a seus clusters
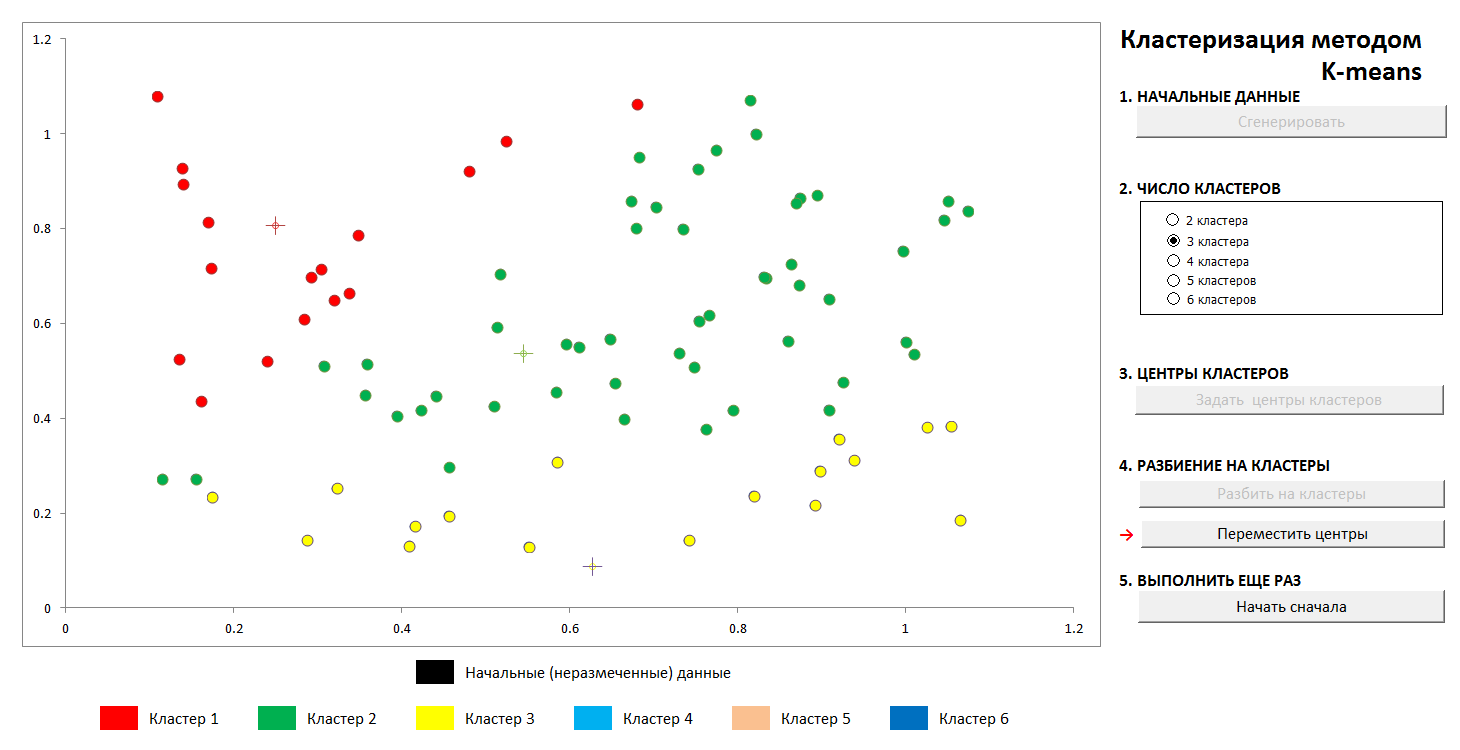
3. Transferência de coordenadas dos centros de aglomerados, recálculo dos pontos, até a estabilização dos centros. A trajetória do centro do cluster para a posição final é visível.

A qualquer momento, você pode definir novos centros de cluster (sem gerar uma nova distribuição de pontos!) E ver que o processo de particionamento nem sempre é exclusivo. Matematicamente, isso significa que, para a função otimizada (a soma dos quadrados das distâncias dos pontos aos centros de seus aglomerados), encontramos um mínimo global, mas local. Esse problema pode ser derrotado por uma escolha não aleatória dos centros iniciais dos clusters ou pela classificação dos centros possíveis (às vezes é vantajoso colocá-los exatamente em algum momento, pelo menos há uma garantia de que não obteremos clusters vazios). De qualquer forma, um conjunto finito sempre tem um limite inferior exato.
Você pode jogar com este arquivo neste link (não se esqueça de ativar o suporte a macro. Os arquivos são verificados quanto a vírus)
Descrição do método Wikipedia - método
k-means2. Aproximação por polinômios e discriminação de dados. Reciclagem
Um notável cientista e popularizador da ciência de dados K.V. Vorontsov fala brevemente sobre métodos de aprendizado de máquina como "a ciência de desenhar curvas através de pontos". Neste exemplo, encontraremos o padrão nos dados pelo método dos mínimos quadrados.
É mostrada a técnica de dividir os dados de origem em "treinamento" e "controle", bem como um fenômeno como reciclagem ou reciclagem para os dados. Com a aproximação correta, teremos um certo erro nos dados de treinamento e um erro um pouco maior nos dados de controle. Se estiver errado, é um ajuste exato aos dados de treinamento e um grande erro no controle.
(É um fato bem conhecido que, através de N pontos, você pode desenhar uma única curva do N-1º grau, e esse método geralmente não fornece o resultado desejado. O
polinômio de interpolação de Lagrange na Wikipedia )
1. Definimos a distribuição inicial

2. Divida os pontos em "treinamento" e "controle" na proporção de 70 para 30.

3. Desenhamos uma curva aproximada para os pontos de treinamento, vemos o erro que isso gera nos dados de controle

4. Traçamos a curva exata através dos pontos de treinamento e vemos um erro monstruoso nos dados de controle (e zero no treinamento, mas qual é o objetivo?).

Obviamente, a variante mais simples com uma única partição nos subconjuntos "treinamento" e "controle" é mostrada; no caso geral, isso é feito repetidamente para o melhor ajuste dos coeficientes.
O arquivo está disponível aqui, antivírus verificado. Ativar macros para funcionar corretamente
3. Dinâmica de descida e erro de gradiente
Haverá um caso 4-dimensional e regressão linear. Os coeficientes de regressão linear serão determinados em etapas pelo método da descida do gradiente, inicialmente todos os coeficientes são zeros. Um gráfico separado mostra a dinâmica da redução de erros, à medida que os coeficientes são cada vez mais ajustados. É possível ver todas as quatro projeções bidimensionais.
Se você definir a etapa de descida do gradiente muito grande, ficará claro que a cada vez que pularmos o mínimo e chegaremos ao resultado em um número maior de etapas, ainda que no final iremos de qualquer maneira (a menos que toque demais na etapa de descida, o algoritmo continuará " no espaçamento "). E o gráfico da dependência do erro na etapa de iteração não será suave, mas "irregular".
1. Gere dados, defina a etapa de descida do gradiente
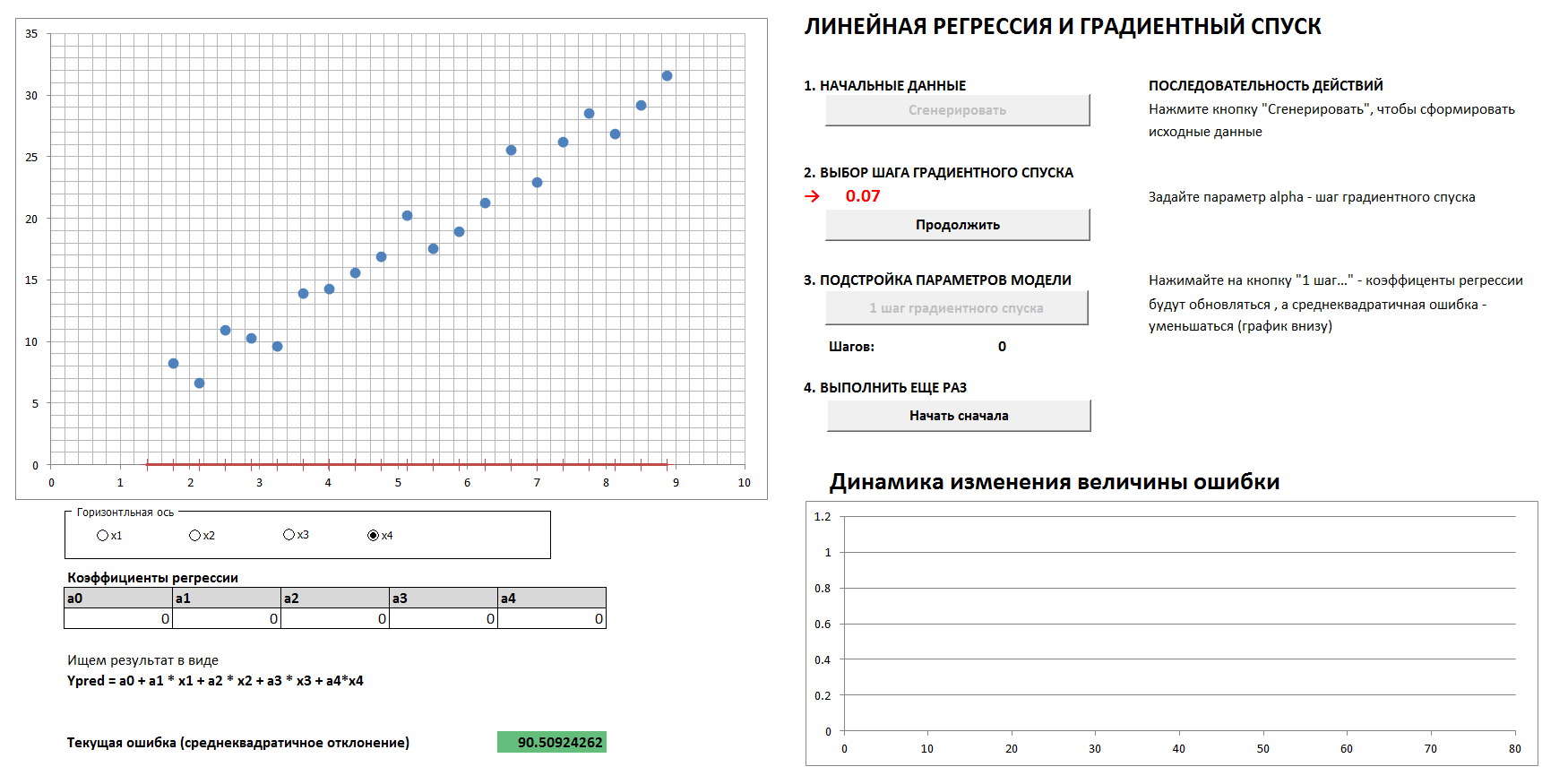
2. Com a escolha certa da etapa de descida do gradiente, chegamos a um nível mínimo e suave

3. Se a etapa de descida do gradiente for selecionada incorretamente, pularemos o máximo, o gráfico de erro será “espasmódico”, a convergência terá um número maior de etapas

e

4. Com uma seleção completamente incorreta da etapa de descida do gradiente, nos afastamos do mínimo

(Para reproduzir o processo com os valores da etapa de descida do gradiente mostrada nas imagens, marque a caixa "dados de referência").
Arquivo - por esse link, você precisa habilitar macros, não há vírus.De acordo com uma comunidade respeitada, tal simplificação e método de apresentação são aceitáveis? Devo traduzir o artigo para o inglês?