É difícil repensar o conceito de tarefa, mas o resultado vale a pena.
 Nota do autor
Nota do autor : Eu sei que calculei incorretamente a transferência de Bragg nos casos clássico e quântico; no entanto, está próximo o suficiente da verdade para entender a diferença entre programar computadores clássicos e quânticos.
Tempo: em algum lugar em 2018. Localização: canal podre em Slaka.
"Você conhece Python?"
As perguntas de John Timmer, diretor científico da Ars Technica, podem às vezes ser surpreendidas. Se fosse possível impregnar cartas em Slaka com cuidado, minha resposta "Sim" simplesmente vazaria com ela.
Acontece que a D-Wave decidiu dar ao mundo acesso ao seu otimizador quântico por meio da API. Ars o convidou para tentar, mas você precisava conhecer Python. Eu estava pronto para isso.
Eu assumi que o D-Wave lançaria algum tipo de API fantástica que poderia pegar meu código proprietário que faz os programadores chorarem e transformá-lo em linhas com otimização quântica. Infelizmente, quando cheguei ao otimizador quântico, descobriu-se que não era. Eu rapidamente me vi imerso na documentação, tentando descobrir o que eu precisava fazer.
Penso que o representante de relações públicas da D-Wave tinha em mente uma pessoa que sabia o suficiente para executar exemplos prontos. Mas sou teimosa. Eu precisava criar três ou quatro tarefas possíveis que queria testar. Eu queria descobrir: posso dominar o processo de solução desses problemas em um computador D-Wave? Quão fácil é dar um salto conceitual da programação clássica para o trabalho com recozimento quântico? Pelo menos algumas das minhas tarefas se encaixam nessa máquina?
Revelando uma conclusão surpreendente imediatamente, direi que as respostas foram as seguintes: talvez não seja "dominar"; difícil; nem todas as tarefas.
Escolha de tarefas para programação
Apesar da maneira como você me imagina, posso ser chamado de programador praticante. Essencialmente, qualquer pessoa com um bom entendimento de programação faria uma careta (e possivelmente cometeria um assassinato) quando vi meu código Python.
No entanto, posso criar tarefas que exijam a criação de um programa para resolvê-las. Eu preciso, por exemplo, de algo que calcule o campo elétrico de um conjunto de eletrodos. Algo que encontra um estado com uma energia mínima de átomo de hélio. Ou algo que conta o aumento da intensidade da luz no início do laser. Essas tarefas me interessam mais. E, iniciando este projeto, não fazia ideia se a arquitetura D-Wave poderia resolver esses problemas.
Escolhi dois problemas que, na minha opinião, poderiam funcionar: encontrar membros do conjunto de Mandelbrot e calcular os contornos potenciais de um conjunto de eletrodos. A vantagem desses problemas era que eu poderia resolvê-los rapidamente usando o código clássico e comparar as respostas. Mas rapidamente encontrei problemas tentando descobrir como começar a resolver esses problemas em uma máquina a partir da D-Wave. Requer uma grande mudança na compreensão das tarefas, e meu pensamento funciona de maneira bastante direta.
Por exemplo, um dos problemas que encontrei é que estamos lidando com números binários de baixo nível (apesar do fato de que eles são expressos na forma de qubits, não bits). Isso significa que, de fato, o programa não possui tipos. Quase toda a minha experiência em programação foi resolver problemas físicos usando tipos numéricos de ponto flutuante.
Você precisa pensar de maneira diferente sobre a tarefa: a resposta deve ser expressa como um número binário (idealmente, verdadeiro ou falso) e toda a física (por exemplo, todos os números de ponto flutuante) deve ser expressa por meio de uma combinação de qubits. Mesmo que minha vida dependesse disso, eu não seria capaz de descobrir como isso pode ser feito em nenhuma das minhas tarefas. Imerso no ensino, permiti que esse problema fervesse um pouco no meu próprio suco.
Seis meses depois, finalmente me deparei com um problema que eu conhecia e que poderia resolver com um computador D-Wave. A passagem da luz através de uma grade de Bragg de fibra pode ser expressa como um problema binário: um fóton saiu do filtro ou não? Toda a física está contida em compostos qubit, e a resposta é extraída da energia da solução.
Bragg gratings
Uma grade de Bragg unidimensional é um material multicamada. Cada intervalo entre as duas camadas reflete uma pequena quantidade de luz. A penetração total em toda a estrutura é determinada pela distância entre as lacunas. Para que a luz passe, é necessário que as ondas de diferentes intervalos se acumulem na fase. O espectro de passagem de uma grade Bragg ideal com 50 camadas e uma refletância de 0,1% é mostrado abaixo.
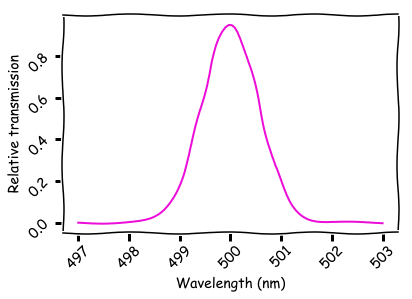
O código a seguir gera dados para este gráfico:
ld = np.linspace(ld_center-3e-9, ld_center+3e-9, num_ld) k = 2*np.pi/ld T = np.ones(ld.shape) for j in range(num_layers): T = T*(1-A)*np.cos(j*k*layer_sep)**2
Aqui calculamos explicitamente as contribuições relativas de cada intervalo, expressas em potência óptica, que atingem o próximo intervalo. As interferências construtivas e destrutivas são levadas em consideração pela redução ou aumento da contribuição do intervalo, dependendo de quão perto a distância entre as camadas coincide com metade do comprimento de onda.
Esse hack é necessário porque a conexão dos qubits é expressa apenas em números reais e não em números complexos (a física é melhor expressa através de números complexos que contêm a amplitude e a fase da luz). No entanto, a saída do código clássico parece aproximadamente correta - a ausência de bandas de frequência lateral preocupa um pouco, o que indica a incompletude do modelo, mas até agora isso não importa.
O código do modelo clássico não possui verificações de consistência. Eu calculei o resultado, sugerindo exatamente como a onda se propagaria. Mesmo que essa suposição seja incorreta, o resultado do cálculo será o mesmo - embora todas as equações sejam baseadas na física, é impossível garantir no código que elas a descrevem corretamente.
Passamos para quanta
No sistema D-Wave, é necessário criar uma cadeia de qubits, cada um dos quais representa a intensidade da luz no intervalo. Cada qubit está associado aos seus vizinhos, e o peso da conexão representa a passagem de um espaço para outro, levando em consideração a distância entre as interfaces. Se a distância entre as interfaces for igual à metade do comprimento de onda, a luz poderá ressoar entre as duas interfaces e passar adiante. Se a distância é um quarto do comprimento de onda, a interferência destrutiva é acionada e a conexão deve ser mínima.
A passagem por um intervalo é indicada em 99,9%, portanto, a conexão entre o zero e o primeiro qubits é
Entre o primeiro e o segundo:
Entre o segundo e o terceiro:
Nesta fórmula, d é a distância física entre as camadas e λ é o comprimento de onda. Se d / λ = 0,5, então o cosseno é igual à unidade, e podemos esperar a transmissão ideal da luz.
No sistema D-Wave, isso significa que todos os dois qubits vizinhos devem ser conectados da seguinte maneira:
Nesta expressão, o grau u leva em consideração a influência de qubits anteriores e simplifica o esquema de conexão.
Implementação de tarefas
Agora, sabendo como conectar qubits, devemos examinar a conexão física de qubits para decidir como concluir esta tarefa. Isso é chamado de incorporação menor.
Devemos fornecer ao computador uma lista de conexões entre qubits e seus pesos. Também devemos especificar desvios indicando a importância de cada qubit. No nosso caso, todos os qubits são igualmente importantes, portanto, são definidos como -1 para todos os qubits (peguei esse número no exemplo padrão). Desvios e conexões devem estar associados a qubits físicos e aos relacionamentos entre eles. No caso de grandes tarefas, a pesquisa para esse mapeamento pode levar muito tempo.
O código para gerar relacionamentos e desvios é bastante simples.
Felizmente, a API do D-Wave tentará encontrar uma pequena implementação por conta própria. Descobri que funcionava para um filtro com 50 camadas, mas não conseguia lidar com 100 camadas. Isso me parece bastante estranho, já que com 2.000 qubits e um comprimento de cadeia de 1 (não precisamos combinar vários qubits físicos para criar um lógico), o sistema deve ser capaz de implementar problemas ainda maiores. Olhando para trás, acredito que a falha ocorreu devido ao fato de eu ter solicitado muitas conexões nulas.
Uma abordagem alternativa é simplesmente não definir explicitamente títulos nulos. Isso dá ao algoritmo a liberdade de encontrar mais opções de implementação nas quais os qubits não têm conexões. Eu não tentei isso, mas essa opção me parece o próximo passo lógico.
De qualquer forma, iniciar a máquina D-Wave é muito simples:
response = EmbeddingComposite(DWaveSampler()).sample_qubo(Q_auto, num_reads=num_runs)
Aprendendo a falar cubitly
A diferença entre o meu algoritmo clássico e a solução D-Wave é que o computador D-Wave não retorna diretamente um resultado claro. Acontece quebrado em muitas partes. Temos uma lista de energias, e a menor delas deve ser a solução. Para várias execuções (digamos 1000) para cada energia, obtemos o número de vezes que ela apareceu na resposta. E para cada execução, obtemos uma "resposta", o valor dos qubits. Não ficou imediatamente claro para mim qual desses valores pode (e pode) ser interpretado como passando por um filtro.
No final, decidi que a energia mínima da solução seria a melhor resposta, pois esse valor, em certo sentido, representa a quantidade de energia armazenada no filtro. Portanto, uma solução com maior energia representa uma maior permeabilidade do filtro, como mostrado abaixo. Transformar esta resposta em uma passagem real de luz é deixada como lição de casa para quem entende isso.

Também é possível obter uma representação física do processo examinando os valores dos qubits em uma solução com a menor energia. Abaixo você pode ver os valores de bit das soluções correspondentes ao pico da curva de transmissão (500 nm), transmissão de 50% (500,6 nm) e transmissão de 5% (501,4 nm).
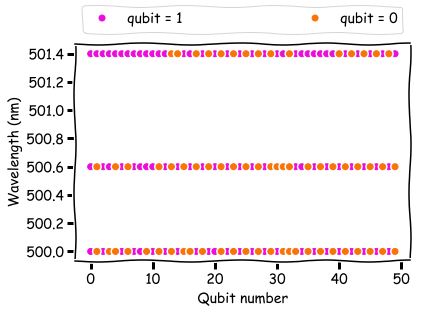
No limite do pico de transmissão, os qubits tendem a se acumular em grupos de unidades. No pico, os qubits alternam entre 0 e 1. Esta última solução é uma imagem binária de como a intensidade da luz na grade de Bragg varia. Em outras palavras, a solução D-Wave também apresenta a física diretamente, o que não pode ser dito sobre o meu código clássico.
Essa é a força real do recozimento quântico. Sim, posso derivar perfeitamente a curva de passagem pelo filtro a partir de cálculos clássicos. Mas, para ter uma ideia do que realmente está acontecendo lá dentro, você precisa de um código mais complexo. E no recozimento quântico, isso é totalmente gratuito. Na minha opinião, isso é muito legal.
Outra vantagem do recozimento quântico é que ele garante uma solução consistente dentro da estrutura da minha escolha de pesos de títulos de qubit. Isso significa que a solução de um computador quântico provavelmente será mais confiável do que a solução obtida no código clássico.
Discussões sobre programação quântica
A parte mais difícil da programação de uma máquina D-Wave é que você precisa pensar de maneira diferente sobre as tarefas. Por exemplo, me acostumei a problemas de minimização quando a curva coincidia com os dados. Mas achei muito difícil mudar a maneira como você pensa sobre um problema físico para começar a escrever o código para resolvê-lo. Não ajuda que a maioria dos exemplos dados pela empresa pareça abstrata e não adaptável a problemas físicos para mim. Mas essa situação mudará quando mais e mais usuários começarem a publicar seu código.
Além disso, podem surgir dificuldades com a interpretação da resposta. Basicamente, gostei da simplicidade da API e é ótimo obter idéias adicionais gratuitamente. Num futuro próximo, eu poderia usar o D-Wave para resolver problemas reais.