"Que tipo de diabo devo lembrar de cor todos esses malditos algoritmos e estruturas de dados?"
Sobre isso, resume-se aos comentários da maioria dos artigos sobre a passagem de entrevistas técnicas. A tese principal, como regra, é que tudo o que é usado de uma maneira ou de outra já foi implementado dez vezes e é mais improvável que esse programador comum precise lidar com isso. Bem, até certo ponto isso é verdade. Mas, como se viu, nem tudo foi implementado, e eu, infelizmente (ou felizmente?), Ainda tive que criar uma estrutura de dados.
Merkle modificado misterioso Patricia Trie.
Como não há informações sobre essa árvore no habr e no meio - um pouco mais, quero lhe dizer que tipo de animal é e com que é comido.

O que é isso
Isenção de responsabilidade: a principal fonte de informações para implementação para mim foi o Livro Amarelo , bem como os códigos - fonte parity-ethereum e go-ethereum . Havia um mínimo de informações teóricas sobre a justificativa de certas decisões; portanto, todas as conclusões sobre os motivos para tomar certas decisões são minhas. Caso eu esteja enganado em alguma coisa - terei prazer em corrigir os comentários.
Uma árvore é uma estrutura de dados que é um gráfico acíclico conectado. Tudo é simples aqui, todos estão familiarizados com isso.
A árvore de prefixos é a árvore raiz na qual os pares de valores-chave podem ser armazenados devido ao fato de os nós serem divididos em dois tipos: aqueles que contêm parte do caminho (prefixo) e os nós folha que contêm o valor armazenado. Um valor está presente em uma árvore se, e somente se, usando a chave, pudermos percorrer todo o caminho desde a raiz da árvore e encontrar um nó com um valor no final.
A árvore PATRICIA é uma árvore de prefixo na qual os prefixos são binários - ou seja, cada nó-chave armazena informações sobre um bit.
A árvore Merkle é uma árvore de hash construída sobre algum tipo de cadeia de dados, agregando esses mesmos hashes em um (raiz), armazenando informações sobre o estado de todos os blocos de dados. Ou seja, o hash raiz é um tipo de "assinatura digital" do estado da cadeia de blocos. Essa coisa é usada ativamente na blockchain, e mais sobre ela pode ser encontrada aqui .

Total: Merkle modificado Patricia Trie (daqui em diante MPT) é uma árvore de hash que armazena pares de valores-chave, enquanto as chaves são apresentadas em formato binário. E o que exatamente é "Modificado", descobriremos um pouco mais tarde quando discutirmos a implementação.
Por que isso?
O MPT é usado no projeto Ethereum para armazenar dados sobre contas, transações, resultados de sua execução e outros dados necessários para o funcionamento do sistema.
Ao contrário do Bitcoin, no qual o estado está implícito e é calculado por cada nó de forma independente, o saldo de cada conta (assim como os dados a ela associados) são armazenados diretamente no blockchain no ar. Além disso, a localização e a imutabilidade dos dados devem ser fornecidas criptograficamente - poucas pessoas usarão criptomoeda na qual o saldo de uma conta aleatória pode mudar sem razões objetivas.
O principal problema enfrentado pelos desenvolvedores do Ethereum é a criação de uma estrutura de dados que pode efetivamente armazenar pares de valores-chave e, ao mesmo tempo, fornecer verificação dos dados armazenados. Então MPT apareceu.
Como é isso?
MPT é um prefixo PATRICIA em que as chaves são seqüências de bytes.
As arestas nesta árvore são sequências de mordidelas (meio bytes). Assim, um nó pode ter até dezesseis descendentes (correspondendo a ramificações de 0x0 a 0xF).
Os nós são divididos em 3 tipos:
- Nó da filial. O nó usado para ramificação. Contém até 1 a 16 links para nós filho. Também pode conter um valor.
- Nó de extensão. Um nó auxiliar que armazena parte do caminho comum a vários nós filhos, além de um link para o nó da filial, que fica abaixo.
- Nó folha. Um nó que contém parte do caminho e valor armazenado. É o fim da cadeia.
Como já mencionado, o MPT é construído sobre outro repositório kv, que armazena nós na forma de "link" => "nó codificado RLP ".
E aqui chegamos a um novo conceito: RLP. Em resumo, esse é um método de codificação de dados que representa listas ou sequências de bytes. Exemplo: [ "cat", "dog" ] = [ 0xc8, 0x83, 'c', 'a', 't', 0x83, 'd', 'o', 'g' ] . Não entrarei em detalhes em particular, e na implementação utilizo uma biblioteca pronta, pois a cobertura deste tópico também inflará um artigo já bastante grande. Se você ainda estiver interessado, pode ler mais aqui . Nós nos limitamos ao fato de podermos codificar dados no RLP e decodificá-los de volta.
Um link para um nó é definido da seguinte maneira: se o comprimento do nó codificado RLP for 32 ou mais bytes, o link será um hash keccak da representação RLP do nó. Se o comprimento for menor que 32 bytes, o link será a representação RLP do próprio nó.
Obviamente, no segundo caso, você não precisa salvar o nó no banco de dados, porque ele será salvo inteiramente dentro do nó pai.

A combinação de três tipos de nós permite que você armazene dados de maneira eficaz no caso de poucas chaves (a maioria dos caminhos será armazenada nos nós de extensão e folha, e haverá poucos nós de ramificação) e no caso de muitos nós (os caminhos não serão armazenados explicitamente, mas eles "se reunirão" durante a passagem pelos nós de ramificação).
Um exemplo completo de uma árvore usando todos os tipos de nós:
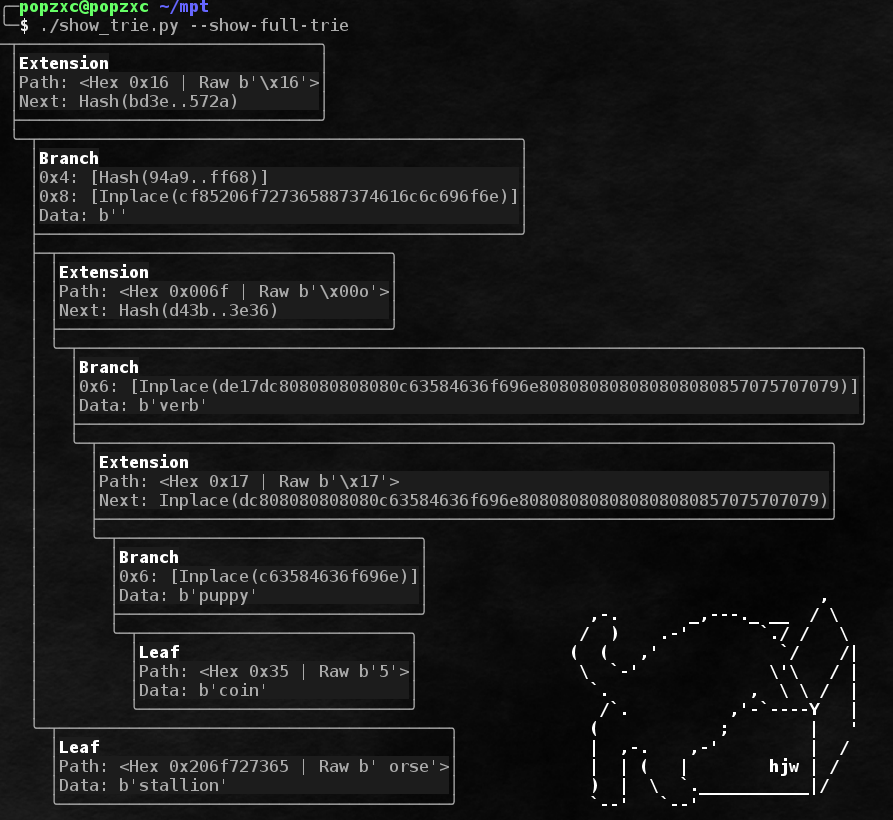
Como você deve ter notado, as partes armazenadas dos caminhos têm prefixos. Os prefixos são necessários para vários propósitos:
- Para distinguir nós de extensão de nós folha.
- Para alinhar seqüências de um número ímpar de petiscos.
As regras para criar prefixos são muito simples:
- O prefixo leva 1 mordidela. Se o comprimento do caminho (excluindo o prefixo) for ímpar, o caminho começará imediatamente após o prefixo. Se o comprimento do caminho for par, para alinhar após o prefixo, o nibble 0x0 será adicionado primeiro.
- O prefixo é inicialmente 0x0.
- Se o comprimento do caminho for ímpar, 0x1 será adicionado ao prefixo, se for par - 0x0.
- Se o caminho levar a um nó Folha, 0x2 será adicionado ao prefixo, se 0x0 for adicionado ao nó Extensão.
Em beatiks, eu acho, será mais claro:
0b0000 => , Extension 0b0001 => , Extension 0b0010 => , Leaf 0b0011 => , Leaf
Exclusão que não é exclusão
Apesar do fato de a árvore ter a operação de excluir nós, de fato, tudo o que foi adicionado permanece na árvore para sempre.
Isso é necessário para não criar uma árvore completa para cada bloco, mas armazenar apenas a diferença entre as versões antiga e nova da árvore.
Assim, usando diferentes hashes de raiz como ponto de entrada, podemos obter qualquer um dos estados em que a árvore já esteve.

Essas nem todas são otimizações. Há mais, mas não vamos falar sobre isso - e, portanto, o artigo é amplo. No entanto, você pode ler por si mesmo.
Implementação
A teoria acabou, vamos para a prática. Usaremos a lingua franca do mundo da TI, que é python .
Como haverá muito código e, para o formato do artigo, muito precisará ser reduzido e dividido, deixarei imediatamente um link para o github .
Se necessário, você pode ver a imagem inteira.
Primeiro, definimos a interface em árvore que queremos obter como resultado:
class MerklePatriciaTrie: def __init__(self, storage, root=None): pass def root(self): pass def get(self, encoded_key): pass def update(self, encoded_key, encoded_value): pass def delete(self, encoded_key): pass
A interface é extremamente simples. As operações disponíveis estão recebendo, excluindo, inserindo e alterando (combinadas na atualização), além de obter o hash raiz.
O armazenamento será transferido para o método __init__ - uma estrutura de dados semelhante a um dict na qual armazenaremos os nós e a root - o "topo" da árvore. Se None for passado como root , assumimos que a árvore está vazia e funciona do zero.
_ Observação: você pode estar se perguntando por que as variáveis nos métodos são nomeadas como encoded_key e encoded_value , e não apenas key / value . A resposta é simples: de acordo com a especificação, todas as chaves e valores devem ser codificados no RLP . Não nos incomodaremos com isso e deixaremos essa ocupação nos ombros dos usuários da biblioteca.
No entanto, antes de começarmos a implementar a própria árvore, duas coisas importantes devem ser feitas:
- Implemente a classe
NibblePath , que é uma cadeia de petiscos, para não codificá-los manualmente. - Implementar a classe
Node dentro da estrutura desta classe - Extension , Leaf e Branch .
Nibblepath
Então, NibblePath . Como iremos mover ativamente a árvore, a base da funcionalidade de nossa classe deve ser a capacidade de definir o "deslocamento" desde o início do caminho, além de receber uma mordidela específica. Sabendo disso, definimos a base da nossa classe (bem como algumas constantes úteis para trabalhar com os prefixos abaixo):
class NibblePath: ODD_FLAG = 0x10 LEAF_FLAG = 0x20 def __init__(self, data, offset=0): self._data = data
Muito simples, não é?
Resta escrever apenas funções para codificar e decodificar uma sequência de petiscos.
class NibblePath:
Em princípio, este é o mínimo necessário para um trabalho conveniente com mordidelas. Obviamente, na implementação atual ainda existem vários métodos auxiliares (como combine , mesclar dois caminhos em um), mas sua implementação é muito trivial. Se estiver interessado, a versão completa pode ser encontrada aqui .
Nó
Como já sabemos, nossos nós são divididos em três tipos: Folha, Extensão e Ramo. Todos eles podem ser codificados e decodificados, e a única diferença são os dados armazenados dentro. Para ser honesto, é isso que os tipos de dados algébricos são solicitados e, em Rust , por exemplo, eu escreveria algo no espírito:
pub enum Node<'a> { Leaf(NibblesSlice<'a>, &'a [u8]), Extension(NibblesSlice<'a>, NodeReference), Branch([Option<NodeReference>; 16], Option<&'a [u8]>), }
No entanto, como não existe ADT no python, definiremos a classe Node e, dentro dela, existem três classes correspondentes aos tipos de nós. Implementamos a codificação diretamente nas classes de nós e a decodificação na classe Node .
A implementação, no entanto, é elementar:
Folha:
class Leaf: def __init__(self, path, data): self.path = path self.data = data def encode(self):
Extensão:
class Extension: def __init__(self, path, next_ref): self.path = path self.next_ref = next_ref def encode(self):
Filial:
class Branch: def __init__(self, branches, data=None): self.branches = branches self.data = data def encode(self):
Tudo é muito simples. A única coisa que pode causar perguntas é a função _prepare_reference_for_encoding .
Então eu confesso, tive que usar uma muleta pequena. O fato é que a biblioteca rlp decodifica os dados recursivamente, e o link para outro nó, como sabemos, pode ser dados rlp (caso o nó codificado tenha menos de 32 caracteres). Trabalhar com links em dois formatos - bytes de hash e um nó decodificado - é muito inconveniente. Portanto, escrevi duas funções que, após decodificar o nó, retornam os links no formato de bytes e decodificam-nos, se necessário, antes de salvar. Essas funções são:
def _prepare_reference_for_encoding(ref):
Termine com nós escrevendo uma classe Node . Haverá apenas dois métodos: decodificar o nó e transformá-lo em um link.
class Node:
Uma pausa
Fuh! Há muita informação. Eu acho que é hora de relaxar. Aqui está outro gato para você:
Milota, certo? Ok, de volta às nossas árvores.
MerklePatriciaTrie
Hurrah - elementos auxiliares estão prontos, passamos aos mais deliciosos. Por precaução, lembrarei a interface da nossa árvore. Ao mesmo tempo, implementamos o método __init__ .
class MerklePatriciaTrie: def __init__(self, storage, root=None): self._storage = storage self._root = root def root(self): pass def get(self, encoded_key): pass def update(self, encoded_key, encoded_value): pass def delete(self, encoded_key): pass
Mas com os métodos restantes, trataremos um por um.
obter
O método get (como, em princípio, os outros métodos) consistirá em duas partes. O próprio método preparará os dados e trará o resultado para a forma esperada, enquanto o trabalho real ocorrerá dentro do método auxiliar.
O método básico é extremamente simples:
class MerklePatriciaTrie:
No entanto, _get não _get muito mais complicado: para chegar ao nó desejado, precisamos ir da raiz para todo o caminho fornecido. Se no final encontramos um nó com dados (Folha ou Ramo) - viva, os dados são recebidos. Se não foi possível passar, a chave necessária está faltando na árvore.
Implementação:
class MerklePatriciaTrie:
Bem, ao mesmo tempo, escreveremos métodos para salvar e carregar nós. Eles são simples:
class MerklePatriciaTrie:
atualizar
O método de update já é mais interessante. Basta ir até o final e inserir o nó Leaf nem sempre funcionará. É provável que o ponto de separação de chaves esteja em algum lugar dentro do nó Folha ou Extensão já salvo. Nesse caso, você precisará separá-los e criar vários novos nós.
Em geral, toda a lógica pode ser descrita pelas seguintes regras:
- Enquanto o caminho coincide inteiramente com os nós existentes, descemos recursivamente a árvore.
- Se o caminho estiver concluído e estivermos no nó Ramificação ou Folha, significa que a
update simplesmente atualiza o valor correspondente a essa chave. - Se os caminhos estiverem divididos (ou seja, não atualizamos o valor, mas inserimos um novo), e estamos no nó Filial - crie um nó Folha e especifique um link para ele no ramo ramo correspondente.
- Se os caminhos estiverem divididos e estivermos em um nó Folha ou Extensão, precisamos criar um nó Filial que separa os caminhos e, se necessário, um nó Extensão para a parte comum do caminho.
Vamos gradualmente expressar isso no código. Por que gradualmente? Como o método é grande e será difícil entendê-lo em massa.
No entanto, deixarei um link para o método completo aqui .
class MerklePatriciaTrie:
Não há lógica geral suficiente, o mais interessante é if s.
if type(node) == Node.Leaf
Primeiro, vamos lidar com os nós Leaf. Apenas 2 cenários são possíveis com eles:
O restante do caminho que estamos seguindo é exatamente o mesmo que o caminho armazenado no nó Folha. Nesse caso, basta alterar o valor, salvar o novo nó e retornar um link para ele.
Os caminhos são diferentes.
Nesse caso, você precisa criar um nó Filial que separa os dois caminhos.
Se um dos caminhos estiver vazio, seu valor será transferido diretamente para o nó Filial.
Caso contrário, teremos que criar dois nós Leaf encurtados pelo comprimento da parte comum dos caminhos + 1 petisco (esse petisco será indicado pelo índice da ramificação correspondente do nó Branch).
Você também precisará verificar se há uma parte comum do caminho para entender se também precisamos criar um nó de extensão.
No código, ficará assim:
if type(node) == Node.Leaf: if node.path == path:
O procedimento _create_branch_node é o seguinte:
def _create_branch_node(self, path_a, value_a, path_b, value_b):
if type(node) == Node.Extension
No caso do nó Extension, tudo se parece com um nó Leaf.
Se o caminho do nó Extension for um prefixo para o nosso caminho, simplesmente seguiremos recursivamente.
Caso contrário, precisamos fazer a separação usando o nó Filial, como no caso descrito acima.
Por conseguinte, o código:
elif type(node) == Node.Extension: if path.starts_with(node.path):
O procedimento _create_branch_extension logicamente equivalente ao procedimento _create_branch_leaf , mas funciona com o nó Extension.
if type(node) == Node.Branch
Mas com o nó Branch, tudo é simples. Se o caminho estiver vazio, simplesmente salvamos o novo valor no nó Branch atual. Se o caminho não estiver vazio, "morderemos" uma mordidela dele e recursivamente diminuiremos.
O código, eu acho, não precisa de comentários.
elif type(node) == Node.Branch: if len(path) == 0: return self._store_node(Node.Branch(node.branches, value)) idx = path.at(0) new_reference = self._update(node.branches[idx], path.consume(1), value) node.branches[idx] = new_reference return self._store_node(node)
excluir
Fuh! O último método permanece. Ele é o mais alegre. A complexidade da exclusão é que precisamos retornar a estrutura ao estado em que ela teria caído se tivéssemos feito toda a cadeia de update , excluindo apenas a chave excluída.
, , , , . "", , .
. , N- , N+1 . enum — DeleteAction , .
delete :
class MerklePatriciaTrie:
, get update . . .
if type(node) == Node.Leaf
. . — , , .
:
if type(node) == Node.Leaf: if path == node.path: return MerklePatriciaTrie._DeleteAction.DELETED, None else: raise KeyError
, "" — . , . .
if type(node) == Node.Extension
C Extension- :
- , Extension- . — .
_delete , "" .- . :
- . .
- . .
- Branch-. . , Branch- . , , Leaf-. — Extension-.
:
elif type(node) == Node.Extension: if not path.starts_with(node.path): raise KeyError
if type(node) == Node.Branch
.
, . Branch-, …
Porque Branch- Leaf- ( ) Extension- ( ).
, . , — Leaf-. — Extension-. , , 2 — Branch- .
? :
:
- , .
- ,
_delete .
:
elif type(node) == Node.Branch: action = None idx = None info = None if len(path) == 0 and len(node.data) == 0: raise KeyError elif len(path) == 0 and len(node.data) != 0: node.data = b'' action = MerklePatriciaTrie._DeleteAction.DELETED else:
_DeleteAction .
- Branch- , ( , ). .
if action == MerklePatriciaTrie._DeleteAction.UPDATED:
- ( , ), , .
. :
- . , , , . , .
- , . Leaf- . .
- , . , , .
- , , Branch- . ,
_DeleteAction — UPDATED .
if action == MerklePatriciaTrie._DeleteAction.DELETED: non_empty_count = sum(map(lambda x: 1 if len(x) > 0 else 0, node.branches)) if non_empty_count == 0 and len(node.data) == 0:
_build_new_node_from_last_branch .
— Leaf Extension, , .
— Branch, Extension , , Branch.
def _build_new_node_from_last_branch(self, branches):
O resto
. , … root .
Aqui:
class MerklePatriciaTrie:
, .
… . , , Ethereum . , , , . , :)
, , pip install -U eth_mpt — .

Resultados
?
, -, , - , , . — , .
-, , , — . , skip list interval tree, — , , .
-, , . , - .
-, — .
, , — !
: 1 , 2 , 3 . ! , .