🖕🏾 🤰🏾 🌼 Modelamos o algoritmo MUSIC para determinar a direção de chegada de uma onda eletromagnética 🏥 👰🏻 👨🏼‍🍳

aaspcats

Prefácio

Começarei minha introdução de longe. Era uma vez, no distante 2016-2017, seu humilde servo conseguiu fazer um curso de treinamento de seis meses na cidade distante de Ilmenau (Alemanha), onde completou com sucesso (em geral) o programa de mestrado Comunicações e processamento de sinais . O programa não foi fácil, mas agora é agradável recordá-lo. As vezes ...

Portanto, ao final deste treinamento, além do diploma, eu ainda tinha alguns materiais diferentes em mãos, que eu achava errado não compartilhar.

Um desses materiais está na sua frente.

Quais objetivos eu persegui enquanto preparava o seminário :

falar sobre algumas abordagens já "inteligentes" já estabelecidas no tópico dos arranjos de antenas mais acessíveis e fazê-lo em russo;
realize uma pequena simulação no Python 3 para agitar colegas engenheiros de rádio para examinar mais de perto as linguagens de programação (se você ainda não o olhou de perto);
forneça links para boa literatura em inglês - sem ler fontes estrangeiras, agora, infelizmente, em lugar nenhum.

O que considerar :

O método MUSIC (MUltiple SIgnal Classification) - isso, de fato, refere-se à visualização.

Um exemplo de formação de gráfico e o método MVDR pode ser encontrado aqui (se houver perguntas ou sugestões para material adicional, a discussão poderá ser continuada no Github.Gist).

Como eu disse acima, usaremos Python, a saber:

import numpy as np import matplotlib.pyplot as plt

Por que não o MATLAB, um dos candidatos mais populares e convenientes para modelagem de álgebra linear, você pergunta? Porque, quero mostrar que trabalho semelhante pode ser feito em Python, e o escopo do Python é muito mais amplo que o do MATLAB. Portanto, estar familiarizado com a sintaxe do Python é uma coisa útil, na minha opinião.

Vamos começar!

As fórmulas são preparadas através de https://upmath.me/ . Obrigado aos criadores por uma ótima ferramenta!

Declaração do problema

Suponha que exista um conjunto de antenas lineares consistindo em vários elementos espaçados um do outro $\ Delta = \ frac {\ lambda} {2}$ (passo do conjunto de antenas), onde $\ lambda$ - o comprimento da onda eletromagnética portadora (EM).

Ondas eletromagnéticas caem nesse conjunto de antenas de diferentes direções.

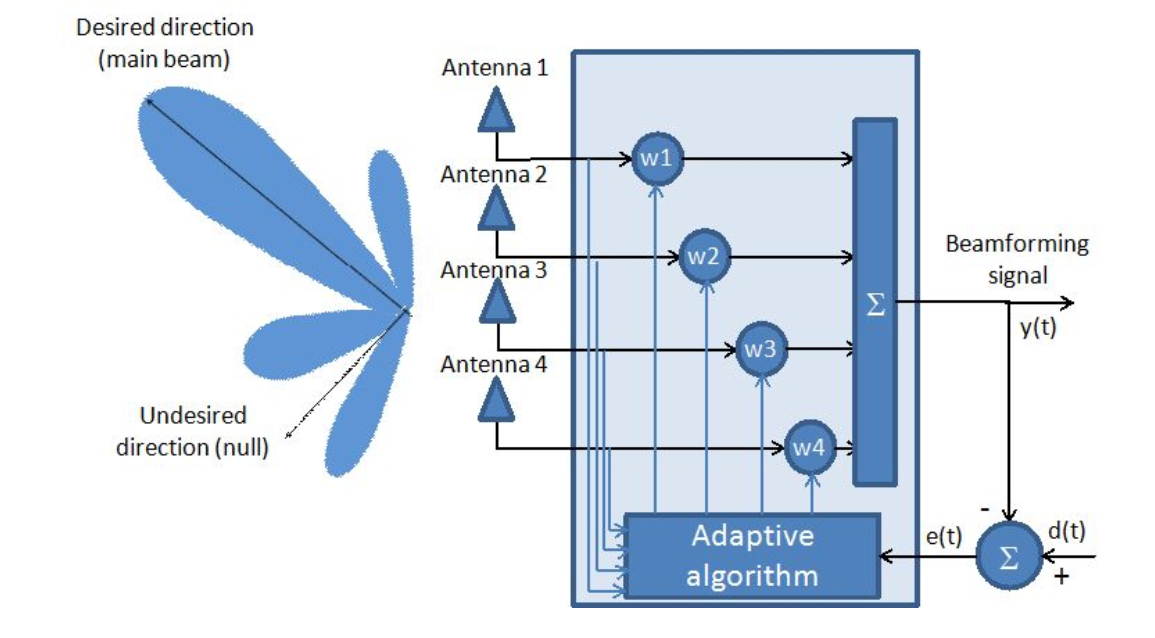
Fig. 1. Sistema de antena adaptável.

Como pode ser visto na figura, o conjunto de antenas é considerado como um filtro adaptável.

Na verdade, encontrar o vetor ideal de coeficientes ( $\ mathbf {w} _ {opt}$ ) é a principal tarefa dos arranjos de antenas adaptáveis do ponto de vista matemático.

Inicialmente, não sabemos de quais direções específicas estão vindo os sinais e quantas delas. Para resolver essa contradição, usaremos o algoritmo MUSIC, um algoritmo para estimar frequências espaciais com alta resolução.

Simulação de sinal recebido

Podemos apresentar o modelo do sinal recebido através da fórmula:

$\ mathbf {X} = \ mathbf {A} \ mathbf {S} + \ mathbf {N}$

onde $\ mathbf {A} = [\ mathbf {a} (\ theta_1) \ quad \ mathbf {a} (\ theta_2) \ quad ... \ quad \ mathbf {a} (\ theta_d)]$ - matriz de vetores de varredura (vetores de direção) do conjunto de antenas ( $a_i = \ exp (-j \ mu m_i)$ , $m = 0, 1 ... (M-1)$ , $M$ - o número de elementos do conjunto de antenas, $d$ - o número de fontes de ondas EM, $\ theta$ - ângulo da direção de chegada da onda EM), $\ mathbf {S}$ - matriz de caracteres transmitidos, e $\ mathbf {N}$ - matriz de ruído aditivo.

Fig. 2. Conjunto de antenas lineares omnidirecionais (ULAA - conjunto de anntenna linear uniforme) [1, p. 32]

Vamos repensar essa fórmula da maneira "cotidiana": em nossa grade, temos uma "bagunça" de vários sinais, que denotamos por $\ mathbf {X}$ . Nós não recebemos explicitamente informações sobre o número de fontes e direções; no entanto, informações sobre isso ainda estão contidas no sinal recebido.

Estamos começando a pesquisar!

Para fazer isso, eles geralmente procedem às manipulações não com as matrizes de amplitudes complexas de sinal, mas com suas covariâncias (isto é, em essência, com poderes):

$\ mathbf {R} _ {xx} = \ mathbf {X} \ mathbf {X} ^ H = \ mathbf {A} \ mathbf {R} _ {ss} \ mathbf {A} ^ H + \ mathbf {R} _ {nn}$

Condições

Introduzimos uma condição importante a ser considerada: o limite de resolução do ângulo Rayleigh:

$sin (\ theta_R) = \ frac {\ lambda} {D}$

onde $D = M \ Delta$ É o comprimento da rede linear.

Redefinimos o ângulo de chegada de uma onda eletromagnética através do conceito de frequência espacial:

$\ mu_R = \ frac {2 \ pi} {\ lambda} \ Delta sin (\ theta_R) = \ frac {2 \ pi} {\ lambda} \ Delta \ frac {\ lambda} {\ Delta M} = \ frac { 2 \ pi} {M}$

onde $\ mu_R$ - existe uma largura padrão do lóbulo principal do feixe ( largura de feixe padrão ).

Para verificar a eficácia do nosso método e sob quais condições, apresentamos alguns valores para a separação angular:

$\ mu_1 = - \ mu_R, \ quad \ mu_2 = 0, \ quad \ mu_3 = \ mu_R \ quad$ - divisão em uma largura de feixe;
$\ mu_1 = -0,5 \ mu_R, \ quad \ mu_2 = 0, \ quad \ mu_3 = 0,5 \ mu_R \ quad$ - divisão na largura de um segundo feixe;
$\ mu_1 = -0,3 \ mu_R, \ quad \ mu_2 = 0, \ quad \ mu_3 = 0,3 \ mu_R \ quad$ - divisão em três décimos da largura do feixe.

Defina os parâmetros de entrada:

 M = 10 #    () SNR = 10 #  - (dB) d = 3 #     N = 50 #  "" (snapshots) S = ( np.sign(np.random.randn(d,N)) + 1j * np.sign(np.random.randn(d,N)) ) / np.sqrt(2) # QPSK W = ( np.random.randn(M,N) + 1j * np.random.randn(M,N) ) / np.sqrt(2) * 10**(-SNR/20) # AWGN #  : # sqrt(N0/2)*(G1 + jG2), #  G1  G2 -   . # .. Es( )  QPSK  1 ,    (noise spectral density): # N0 = (Es/N)^(-1) = SNR^(-1) [] (   ,  SNR = Es/N0); #    : # SNR_dB = 10log10(SNR) => N0_dB = -10log10(SNR) = -SNR_dB []; #    SNR    (..  ),   : # SNR = 10^(SNR_dB/10) => sqrt(N0) = (10^(-SNR_dB/10))^(1/2) = 10^(-SNR_dB/20) mu_R = 2*np.pi / M

Um pouco de teoria sobre o próprio método

Primeiramente, notamos que o progenitor do método MUSIC é o método Pisarenko (1973). O problema considerado do método Pisarenko foi estimar as frequências da soma de exponenciais complexas no ruído branco. V.F. Pisarenko demonstrou que frequências podem ser encontradas a partir de vetores próprios correspondentes ao valor próprio mínimo da matriz de autocorrelação. Posteriormente, esse método se tornou um caso especial do método MUSIC. [2, p. 459]

Schmidt e seus colegas propuseram o algoritmo de classificação de sinais múltiplos (MUSIC) em 1979 [4]. A principal abordagem desse algoritmo é decompor a matriz de covariância do sinal recebido em autovalores. Como esse algoritmo leva em consideração o ruído não correlacionado, a matriz de covariância gerada tem uma forma diagonal. Aqui, os subespaços de sinal e ruído são calculados usando álgebra linear e são ortogonais entre si. Portanto, o algoritmo usa a propriedade de ortogonalidade para extrair os subespaços de sinal e ruído [5].

O algoritmo MUSIC generalizado pode ser definido da seguinte maneira:

Encontre a matriz de covariância $\ mathbf {R} _ {xx}$
Encontre autovetores via EVD ou outro algoritmo numérico adequado:

$\ mathbf {R} _ {xx} = \ mathbf {U} \ mathbf {\ Lambda} \ mathbf {U} ^ H \ qquad (1)$

Encontre o pseudo-espectro (por que com o prefixo pseudo, discutiremos abaixo) MÚSICA através da seguinte fórmula:

$P_ {MU} (e ^ {j \ omega}) = \ frac {1} {\ sum \ limits_ {i = d + 1} ^ {M} | \ mathbf {a} ^ H \ mathbf {u} _i | ^ 2} \ qquad (2)$

onde $\ mathbf {a} = \ begin {bmatrix} e ^ {j0 \ omega} & e ^ {j1 \ omega} & e ^ {j2 \ omega} & ... & e ^ {j (M-1) \ omega } \ end {bmatrix} ^ T$ É o vetor de exponenciais para a frequência ω situada em um determinado intervalo, e $\ mathbf {u} _i$ - o i-ésimo vetor próprio (vetor eigen) da matriz de covariância (1) correspondente ao subespaço de ruído da matriz (1) - daí a indexação com $d + 1$ ( $d$ É a classificação da matriz (1)).

Para maior clareza, tente executar o script MATLAB apropriado fornecido por referência . Preste atenção a dois pontos principais:
em vez de calcular o quadrado da segunda norma no denominador (2), os autores aplicam o algoritmo FFT aos autovetores, o que facilita a modelagem usando funções internas e, em geral, não contradiz a teoria do ponto de vista matemático;
a matriz de covariância é calculada através de matrizes convolucionais; uma abordagem diferente foi mostrada acima para estimar frequências espaciais.

Como você pode imaginar pelo nome, MUSIC também é um método clássico para estimar a direção da recepção em alta resolução. O algoritmo para calcular pseudo-espectros neste contexto é dado abaixo:

encontramos a matriz de covariância do sinal recebido;
encontre o subespaço zero $\ mathbf {U} _0$ :

$\ mathbf {U} = [\ mathbf {U} _s \ quad \ mathbf {U} _0]$

selecione algum intervalo de pesquisa:

$a (\ mu) = \ begin {bmatrix} e ^ {j0 \ mu_1} & ... & e ^ {j0 \ mu_Q} \\ ... & ... & ... \\ e ^ {j ( M-1) \ mu_1} & ... & e ^ {j (M-1) \ mu_Q} \ end {bmatrix}$

onde $\ mu = - \ frac {2 \ pi f_c} {c} \ Delta sin \ theta = - \ frac {2 \ pi} {\ lambda} \ Delta sin \ theta$

calcule o pseudo-espectro:

$P_ {MU} (\ theta) = \ frac {\ mathbf {a} ^ H (\ theta) \ mathbf {a} (\ theta)} {\ mathbf {a} ^ H (\ theta) \ mathbf {U} _0 \ mathbf {U} _0 ^ H \ mathbf {a} (\ theta)}$

A relação entre análise espectral e análise dos ângulos de chegada (DoA - direção do arriaval) das ondas EM é descrita na tabela 1.

Tabela 1 Comunicação entre aplicativos MUSIC : Processamento da matriz de sinais e busca harmônica [6].

Variável	Processamento de matriz de sinal	Pesquisa harmônica
$M$	Número de sensores	O número de períodos
$N$	O número de períodos	Número de experiências
$d$	Número de frentes de onda	O número de componentes complexos
$\ mu$	Frequências espaciais	Frequências normalizadas

Em geral, o processo de recebimento através de matrizes (grades) pode ser comparado com o processo de discretização clássica, porque de fato, cada sensor, recebendo uma onda com um certo atraso de fase (isto é, com um certo atraso de tempo), executa as funções de um pulso delta de amostragem. O número de realizações (experimentos) da análise espectral clássica corresponderá ao número de segmentos de tempo (instantâneos). Cada fonte terá sua própria frente de onda, que é equivalente ao número de sinusóides únicos do sinal no caso de análise espectral.

E agora, de volta ao momento de calcular os autovetores. Já mencionamos acima que vetores $a (\ theta_i) \ epsilon A$ onde $i = 1,2, .., d$ são ortogonais ao subespaço de ruído da matriz de covariância, ou seja:

$a (\ theta_i) ^ TU_0 = 0 ^ T$

Na verdade, vemos um sistema de equações, resolvendo o que podemos encontrar as raízes - vetores próprios. Tal método, em contraste com os algoritmos numéricos (que, como observamos acima, se aplica ao EVD), permite obter valores próprios reais e não aproximados. É por isso que essa abordagem nos permite obter não um pseudoespectro, mas um espectro. A mesma idéia formou a base do algoritmo Root MUSIC .

Modelagem

Fuf! Finalmente, todas as fórmulas são descritas e um pouco explicadas. Podemos começar a modelar.

 cases = [[-1., 0, 1.], [-0.5, 0, 0.5], [-0.3, 0, 0.3],] for idxm, c in enumerate(cases): #   ( ): mu_1 = c[0]*mu_R mu_2 = c[1]*mu_R mu_3 = c[2]*mu_R #   a_1 = np.exp(1j*mu_1*np.arange(M)) a_2 = np.exp(1j*mu_2*np.arange(M)) a_3 = np.exp(1j*mu_3*np.arange(M)) A = (np.array([a_1, a_2, a_3])).T #    X = np.dot(A,S) + W #    R = np.dot(X,np.matrix(X).H) U, Sigma, Vh = np.linalg.svd(X, full_matrices=True) U_0 = U[:,d:] #   thetas = np.arange(-90,91)*(np.pi/180) #   mus = np.pi*np.sin(thetas) #    a = np.empty((M, len(thetas)), dtype = complex) for idx, mu in enumerate(mus): a[:,idx] = np.exp(1j*mu*np.arange(M)) # MVDR: S_MVDR = np.empty(len(thetas), dtype = complex) for idx in range(np.shape(a)[1]): a_idx = (a[:, idx]).reshape((M, 1)) S_MVDR[idx] = 1 / (np.dot(np.matrix(a_idx).H, np.dot(np.linalg.pinv(R),a_idx))) # MUSIC: S_MUSIC = np.empty(len(thetas), dtype = complex) for idx in range(np.shape(a)[1]): a_idx = (a[:, idx]).reshape((M, 1)) S_MUSIC[idx] = np.dot(np.matrix(a_idx).H,a_idx)\ / (np.dot(np.matrix(a_idx).H, np.dot(U_0,np.dot(np.matrix(U_0).H,a_idx)))) plt.subplots(figsize=(10, 5), dpi=150) plt.semilogy(thetas*(180/np.pi), np.real( (S_MVDR / max(S_MVDR))), color='green', label='MVDR') plt.semilogy(thetas*(180/np.pi), np.real((S_MUSIC/ max(S_MUSIC))), color='red', label='MUSIC') plt.grid(color='r', linestyle='-', linewidth=0.2) plt.xlabel('Azimuth angles θ (degrees)') plt.ylabel('Power (pseudo)spectrum (normalized)') plt.legend() plt.title('Case #'+str(idxm+1)) plt.show()

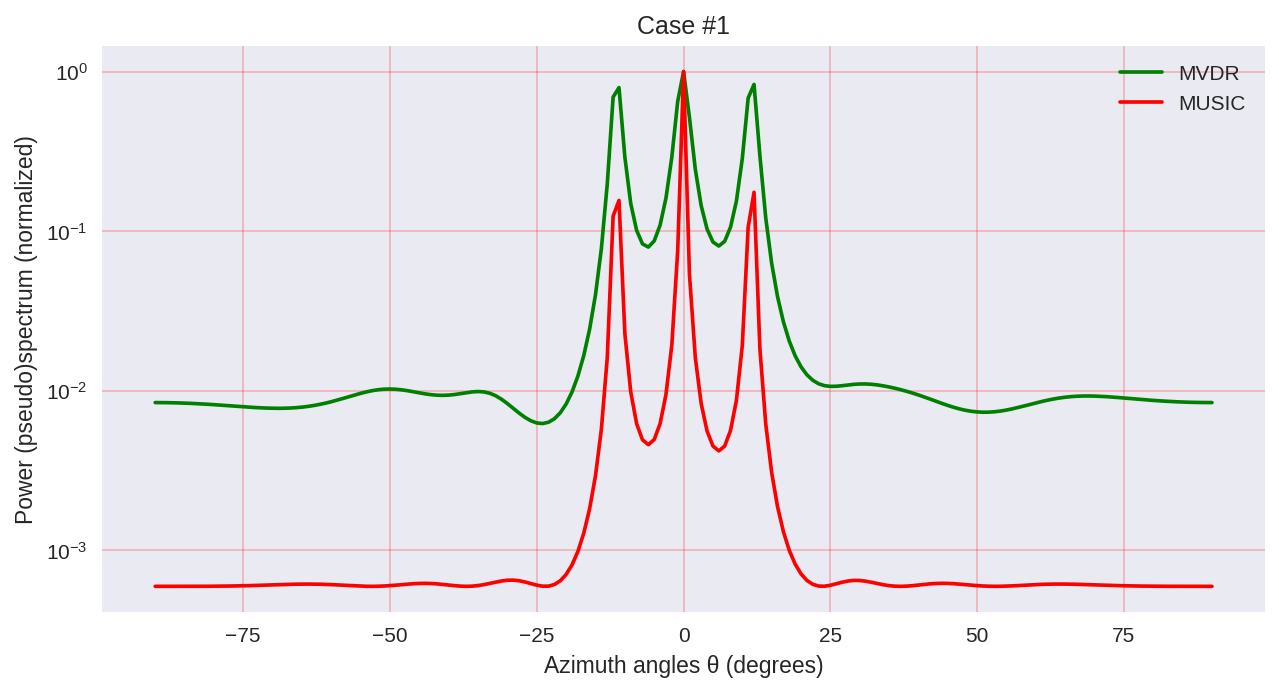
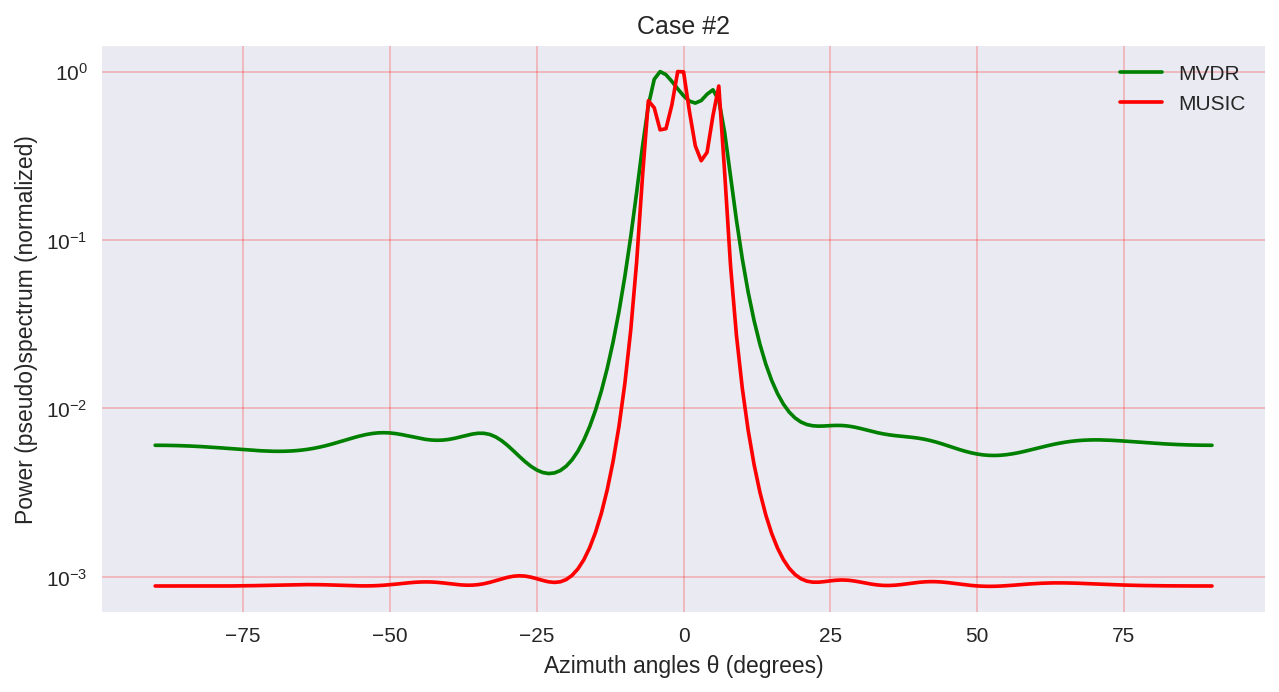
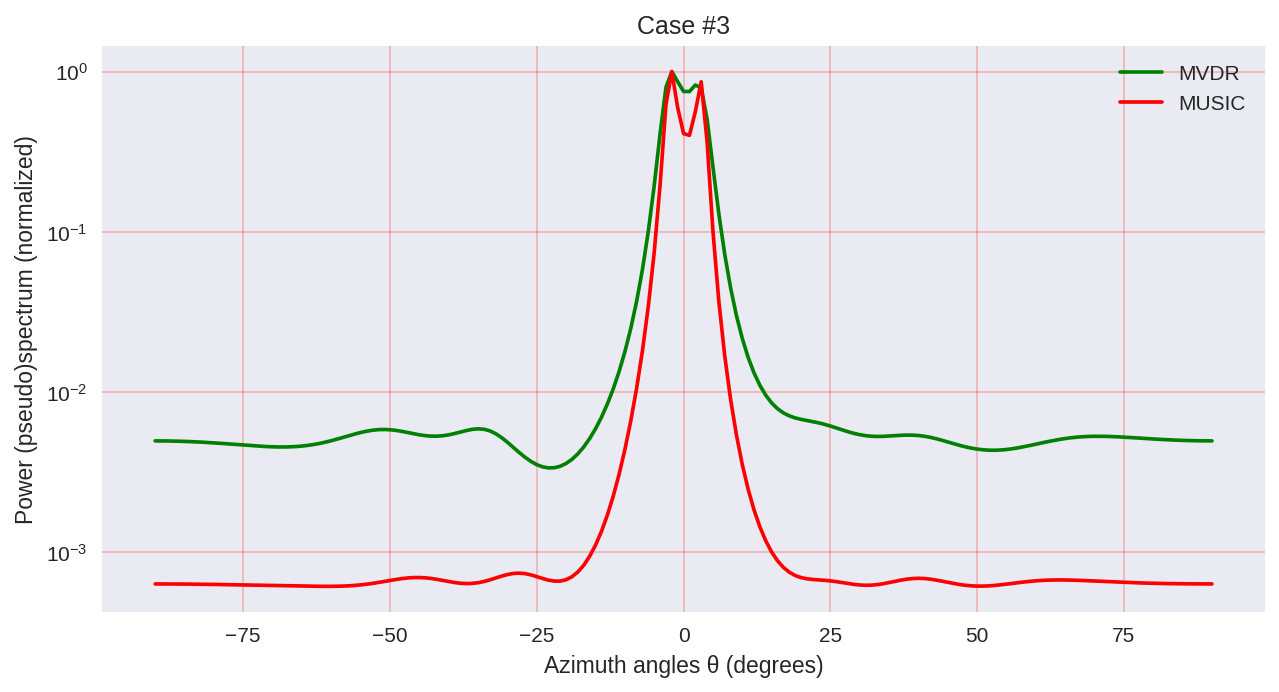
Como podemos ver, a MUSIC possui uma resolução mais alta e permite obter, em geral, melhores resultados do que, por exemplo, o MVDR permite - o mesmo representante dos métodos paramétricos de análise espectral.

No entanto, deve-se ter em mente que, ao usar MUSIC, usamos algoritmos computacionalmente mais caros, como EVD ou SVD, que têm um preço mais alto para maior precisão.

Essas coisas.

Lista de literatura usada:

Haykin, Simon e KJ Ray Liu. Manual sobre processamento de array e redes de sensores. Vol. 63. John Wiley & Sons, 2010. pp. 102-107
Hayes MH Processamento e modelagem estatísticos de sinais digitais. - John Wiley & Sons, 2009.
Haykin, Simon S. Teoria do filtro adaptativo. Pearson Education India, 2008. pp. 422-427
Richmond, Christ D. "Algoritmo de Capon ao quadrado do erro médio - predição SNR e probabilidade de resolução". IEEE Transactions on Signal Processing 53.8 (2005): 2748-2764.
SKP Gupta, MUSIC e algoritmo MUSIC aprimorado para estimar a dor de chegada, IEEE, 2015.
Palestras do professor Martin Haardt ( array array )

Modelamos o algoritmo MUSIC para determinar a direção de chegada de uma onda eletromagnética