Aprendizagem Profunda em Computação Ótica de Fluxo

Com o advento de muitas arquiteturas de redes neurais diferentes, muitas técnicas clássicas de visão computacional são coisa do passado. Cada vez menos pessoas usam SIFT e HOG para detecção de objetos e MBH para reconhecimento de ações e, se elas o usam, são mais como placas artesanais para as grades correspondentes. Hoje, examinaremos um dos problemas clássicos de CV nos quais os métodos clássicos ainda lideram, enquanto as arquiteturas de DL respiram languidamente na parte de trás da cabeça.

Estimativa de fluxo óptico

A tarefa de calcular o fluxo óptico entre duas imagens (geralmente entre quadros adjacentes de um vídeo) é construir um campo vetorial $$$O$do mesmo tamanho, além disso $$$O (i, j)$corresponderá ao vetor de deslocamento de pixel aparente $$$(i, j)$do primeiro quadro para o segundo. Ao construir esse campo vetorial entre todos os quadros adjacentes do vídeo, obtemos uma imagem completa de como certos objetos se moveram nele. Em outras palavras, essa é a tarefa de rastrear todos os pixels em um vídeo. O fluxo óptico é usado de maneira extremamente ampla - em tarefas de reconhecimento de ação, por exemplo, um campo vetorial permite que você se concentre nos movimentos que ocorrem no vídeo e se afasta do seu contexto [7]. Aplicações ainda mais comuns são odometria visual, compactação de vídeo, pós-processamento (por exemplo, adicionando um efeito de câmera lenta) e muito mais.



Há espaço para algumas ambiguidades - o que exatamente é considerado um viés visível do ponto de vista da matemática? Normalmente, supõe-se que os valores de pixel vão de um quadro para o outro sem alterações, ou seja:

$$

$$I (i, j, t) = I (i + u_i, j + u_j, t + 1),$$

onde $$$I (i, j, t)$- intensidade de pixels em coordenadas $$$(i, j)$então fluxo óptico $$$(u_i, u_j)$mostra para onde esse pixel foi movido para o próximo ponto no tempo (ou seja, no próximo quadro).

Na imagem, fica assim:





Visualizar um campo vetorial diretamente com vetores é visual, mas nem sempre é conveniente; portanto, a segunda maneira comum é visualizar com cores:





Cada cor nesta imagem codifica um vetor específico. Para simplificar, vetores maiores que 20 são cortados e o próprio vetor pode ser restaurado por cores a partir da imagem a seguir:




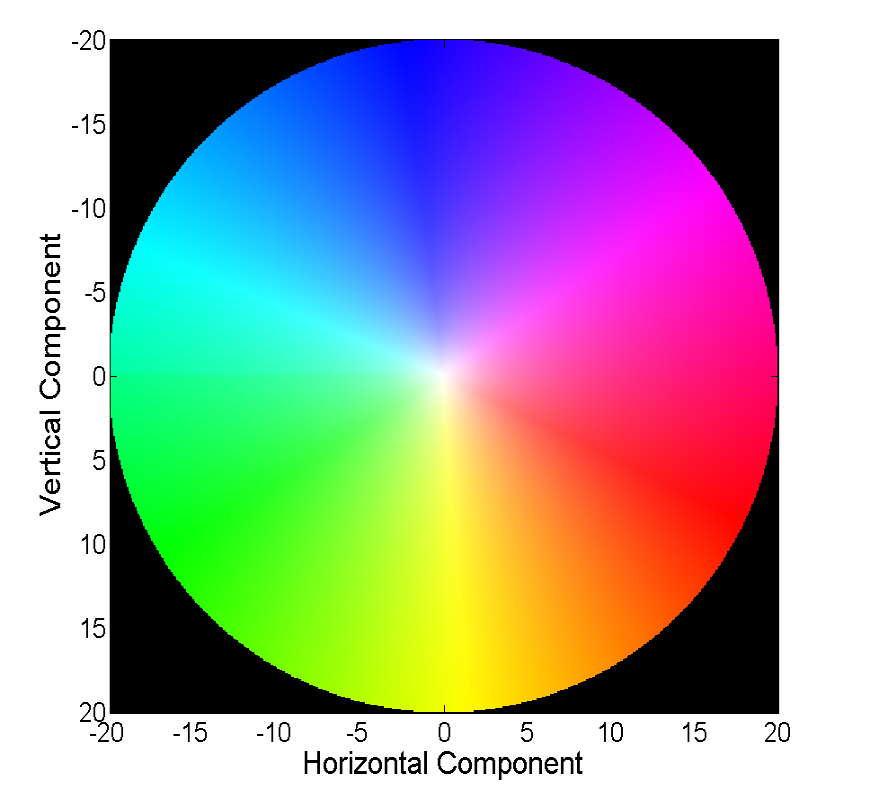
Os métodos clássicos alcançaram uma precisão muito boa, que às vezes tem um preço. Consideraremos o progresso que as redes neurais alcançaram na solução desse problema nos últimos 4 anos.

Dados e métricas

Duas palavras sobre quais conjuntos de dados estavam disponíveis e populares no início de nossa história (ou seja, 2015) e também como eles medem a qualidade do algoritmo resultante.

Middlebury

Um pequeno conjunto de dados de 8 pares de imagens com pequenos desvios, que, no entanto, às vezes é usado na validação de algoritmos para o cálculo do fluxo óptico até agora.

Kitty

Este é um conjunto de dados marcado para aplicativos para carros autônomos e montado usando a tecnologia LIDAR. É amplamente utilizado para validar algoritmos de cálculo de fluxo óptico e contém muitos casos bastante complicados com transições nítidas entre quadros.

Sintel

Outra referência muito comum, criada com base no aberto e desenhado no cartoon Sintel do Blender em duas versões, que são designadas como limpas e finais. O segundo é muito mais complicado, porque contém muitos efeitos atmosféricos, ruído, desfoque e outros problemas para os algoritmos de cálculo do fluxo óptico.

EPE

A função de erro padrão para a tarefa de computação do fluxo óptico é Erro de ponto final ou EPE. Esta é simplesmente a distância euclidiana entre o algoritmo calculado e o verdadeiro fluxo óptico, em média sobre todos os pixels.

Flownet (2015)

Ao iniciar a construção de uma arquitetura de rede neural para a tarefa de calcular o fluxo óptico em 2015, os autores (das universidades de Munique e Freiburg) enfrentaram dois problemas: não havia um grande conjunto de dados marcado para esta tarefa e marcá-la manualmente seria difícil (tente marcar para onde mudei cada pixel da imagem no próximo quadro), primeiro. Essa tarefa era bem diferente de todas as tarefas que foram resolvidas com a ajuda das arquiteturas da CNN antes disso, em segundo lugar. Na verdade, essa é uma tarefa de regressão pixel a pixel, o que a torna semelhante à tarefa de segmentação (classificação pixel a pixel), mas em vez de uma imagem, temos duas entradas e, intuitivamente, os sinais devem mostrar de alguma forma a diferença entre as duas imagens. Como a primeira iteração, foi decidido simplesmente empilhar dois quadros RGB como entrada (tendo recebido, de fato, uma imagem de 6 canais), entre os quais queremos calcular o fluxo óptico, e usar o U-net como uma arquitetura com várias alterações. Essa rede foi chamada FlowNetS (S significa Simple):





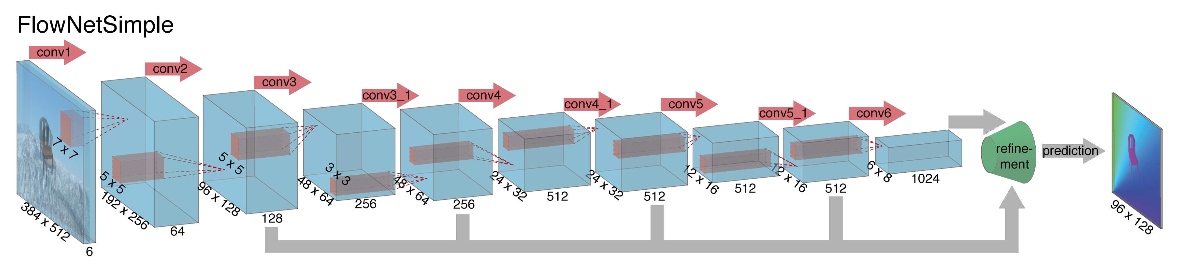
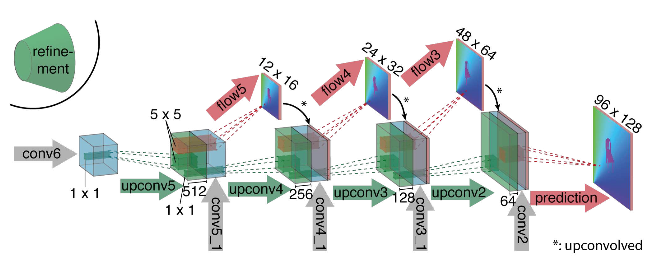
Como você pode ver no diagrama, o codificador não é perceptível, o decodificador difere das opções clássicas de várias maneiras:

1. A previsão do fluxo óptico ocorre não apenas no último nível, mas também em todos os outros. Para obter a verdade da terra para o i-ésimo nível do decodificador, o alvo original (isto é, o fluxo óptico) é simplesmente reduzido (quase o mesmo que a imagem) para a resolução desejada, e o predicado obtido no i-ésimo nível vai além, t ou seja, é concatenado com um mapa de recursos emergindo desse nível. A função geral das perdas de treinamento será uma soma ponderada das perdas de todos os níveis do decodificador, enquanto o próprio peso será maior, quanto mais próximo o nível da saída da rede. Os autores não dão uma explicação de por que isso é feito, mas é mais provável que o motivo seja melhor detectar movimentos nítidos em níveis iniciais, então os vetores no fluxo óptico de baixa resolução não serão tão grandes.
2. O diagrama mostra que a resolução de entrada das imagens é 384x512 e a saída é quatro vezes menor. Os autores notaram que se você aumentar essa saída para 384x512 por interpolação bilinear simples, ela fornecerá a mesma qualidade que se você anexasse mais dois níveis do decodificador. Você também pode usar a abordagem variacional [2], que comprova a qualidade (+ v na tabela com qualidade).
3. Como na U-net, as placas de atributos do codificador são enviadas para o decodificador e concatenadas, conforme mostrado no diagrama.

Para entender como os autores tentaram melhorar sua linha de base, é necessário saber qual é a correlação entre as imagens e por que ela pode ser útil no cálculo do fluxo óptico. Portanto, tendo duas imagens e sabendo que o segundo é o próximo quadro no vídeo em relação ao primeiro, podemos tentar comparar a área ao redor do ponto no primeiro quadro (para o qual queremos encontrar uma mudança para o segundo quadro) com áreas do mesmo tamanho na segunda imagem. Além disso, supondo que a mudança não possa ser muito grande por unidade de tempo, a comparação pode ser considerada apenas em uma determinada vizinhança do ponto de partida. Para isso, a correlação cruzada é usada. Vamos ilustrar com um exemplo.

Pegue dois quadros adjacentes do vídeo, queremos determinar onde um certo ponto mudou do primeiro quadro para o segundo. Suponha que alguma área em torno deste ponto tenha mudado da mesma maneira. De fato, os pixels vizinhos de um vídeo geralmente são deslocados juntos, como provavelmente, visualmente, fazem parte de um objeto. Essa suposição é usada ativamente, por exemplo, em abordagens diferenciais, que podem ser lidas com mais detalhes em [5], [6].

fig, ax = plt.subplots(1, 2, figsize=(20, 10)) ax[0].imshow(frame1) ax[1].imshow(frame2); 

Vamos tentar colocar um ponto no centro da pata do gatinho e encontrá-lo no segundo quadro. Pegue alguma área ao seu redor.

 patch1 = frame1[90:190, 140:250] plt.imshow(patch1); 

Calculamos a correlação entre essa área (na literatura em inglês, muitas vezes escrevemos template ou patch da primeira imagem) e a segunda imagem. O modelo simplesmente "percorre" a segunda imagem e calcula o seguinte valor entre si e as peças do mesmo tamanho na segunda imagem:



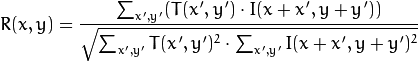
Quanto maior o valor desse valor, mais o modelo se parece com a peça correspondente na segunda imagem. Com o OpenCV, você pode fazer isso:

 corr = cv2.matchTemplate(frame2, patch1, cv2.TM_CCORR_NORMED) plt.imshow(corr, cmap='gray'); 

Mais detalhes podem ser encontrados em [7].

O resultado é o seguinte:



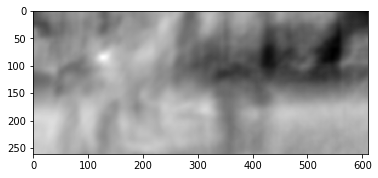
Vemos um pico claro, indicado em branco. Encontre-o no segundo quadro:

 min_val, max_val, min_loc, max_loc = cv2.minMaxLoc(corr) h, w, _ = patch1.shape top_left = max_loc bottom_right = (top_left[0] + w, top_left[1] + h) frame2_copy = frame2.copy() cv2.rectangle(frame2_copy, top_left, bottom_right, 255, 2) plt.imshow(frame2_copy); 

Vemos que o pé foi encontrado corretamente, de acordo com esses dados, podemos entender em qual direção ele se moveu do primeiro quadro para o segundo e calcular o fluxo óptico correspondente. Além disso, verifica-se que esta operação é bastante resistente a distorções fotométricas, ou seja, se o brilho no segundo quadro aumentar bastante, o pico de correlação cruzada entre as imagens permanecerá no lugar.

Considerando tudo o exposto, os autores decidiram introduzir a chamada camada de correlação em sua arquitetura, mas optou-se por não considerar a correlação de acordo com as imagens de entrada, mas de acordo com os mapas de atributos após várias camadas do codificador. Essa camada, por razões óbvias, não possui parâmetros de aprendizado, embora seja essencialmente semelhante à convolução, mas, em vez de filtros, usa não pesos, mas alguma área da segunda imagem:



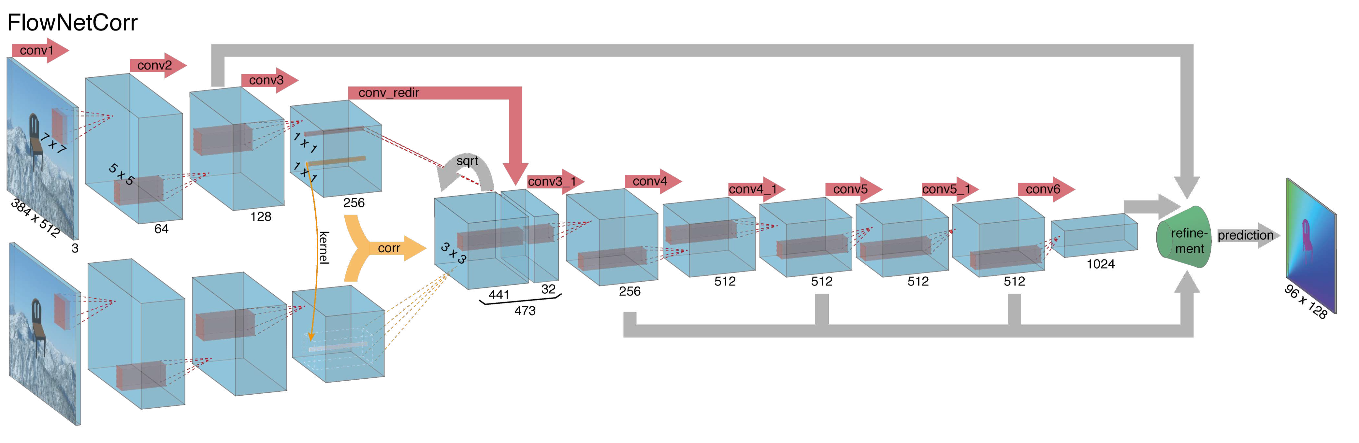
Curiosamente, esse truque não deu uma melhora significativa na qualidade dos autores deste artigo, no entanto, foi aplicado com mais êxito em trabalhos posteriores, e em [9] os autores foram capazes de mostrar que, mudando ligeiramente os parâmetros de treinamento, o FlowNetC pode funcionar muito melhor.

Os autores resolveram o problema com a falta de um conjunto de dados de uma maneira bastante elegante: eles copiaram 964 imagens do Flickr sobre os temas: "cidade", "paisagem", "montanha" na resolução de 1024 × 768 e usaram sua colheita 512 × 384 como pano de fundo, que depois gerou alguns cadeiras de um conjunto aberto de modelos 3D renderizados. Em seguida, várias transformações afins foram aplicadas independentemente às cadeiras e ao fundo, usadas para gerar a segunda imagem em um par e o fluxo óptico entre elas. O resultado é o seguinte:





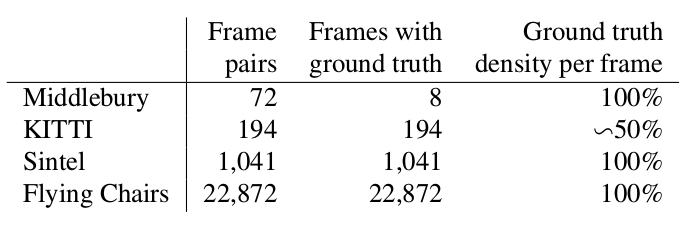
Um resultado interessante foi que o uso de um conjunto de dados sintético tornou possível obter uma qualidade relativamente boa para dados de outro domínio. A sintonia fina nos dados correspondentes, é claro, provou mais qualidades (+ pés na tabela abaixo):



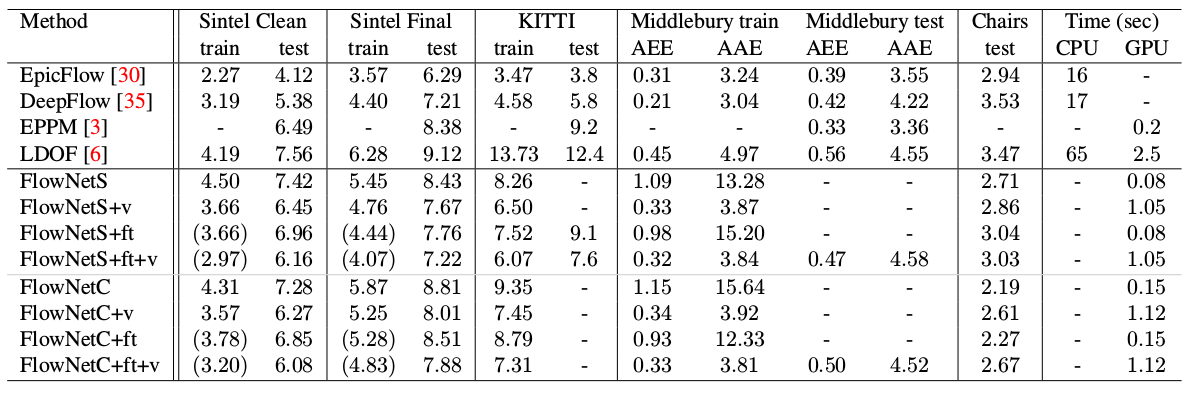
O resultado em vídeos reais pode ser visto aqui:

SpyNet (2016)

Em muitos artigos subseqüentes, os autores tentaram melhorar a qualidade, resolvendo o problema do fraco reconhecimento de movimentos bruscos. Intuitivamente, o movimento não será capturado pela rede se seu vetor ultrapassar significativamente o campo receptivo de ativação. Propõe-se resolver este problema devido a três fatores: uma convolução maior, pirâmides e "distorcer" uma imagem de um par em um fluxo óptico. Tudo em ordem.

Portanto, se tivermos algumas imagens nas quais o objeto mudou nitidamente (mais de 10 pixels), podemos simplesmente reduzir a imagem (em 6 ou mais vezes). O valor absoluto do deslocamento diminuirá significativamente, e é mais provável que a rede seja capaz de “capturá-lo”, especialmente se suas convoluções forem maiores que o próprio deslocamento (neste caso, convoluções 7x7 são usadas).



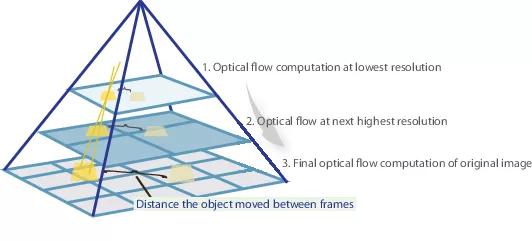
No entanto, ao reduzir a imagem, perdemos muitos detalhes importantes; portanto, devemos ir para o próximo nível da pirâmide, no qual o tamanho da imagem já é maior, considerando de alguma forma as informações que recebemos antes quando calculamos o fluxo óptico em um tamanho menor. Isso é feito usando o operador de distorção, que narra a primeira imagem de acordo com a aproximação disponível do fluxo óptico (obtido no nível anterior). Uma melhoria nesse caso é que a primeira imagem que é "empurrada" de acordo com a aproximação do fluxo óptico estará mais próxima da segunda do que a original, ou seja, reduziremos novamente o valor absoluto do fluxo óptico, que precisamos prever (lembre-se, pequeno em valor os movimentos são detectados muito melhor, pois são completamente incluídos em uma convolução). Do ponto de vista da matemática, tendo uma imagem de bitmap I e aproximação do fluxo óptico V, o operador de distorção pode ser descrito da seguinte maneira:

$$

$$w (I, V) = I_w, \; \; I_w (x) = I (x + V (x)),$$

onde $$$x = (i, j)$, ou seja, um ponto específico na imagem $$$I$- a própria imagem $$$V$- fluxo óptico $$$I_w$- a imagem resultante, "encapsulada" no fluxo óptico.

Como aplicar tudo isso na arquitetura da CNN? Fixamos o número de níveis da pirâmide $$$k$e um fator pelo qual cada imagem subseqüente é reduzida em um nível a partir da última $$$n$. Denotar por $$$d (*)$e $$$u (*)$as funções de downsampling e upsampling da imagem ou fluxo óptico por esse fator.

Também receberemos um conjunto de CNN-ok { $$$G_0 ... G_k$}, um para cada nível da pirâmide. Então $$$G_i$-a rede aceitará algumas imagens com $$$i$pirâmide e fluxo óptico calculados em $$$G_ {i-1}$nível ( $$$G_0$apenas aceitará um tensor de zeros). Nesse caso, enviaremos uma das imagens para a camada de distorção para reduzir a diferença entre elas e não preveremos o fluxo óptico nesse nível, mas o valor que precisa ser adicionado ao fluxo óptico aumentado (ampliado) do nível anterior para obter o fluxo óptico neste nível. Na fórmula, parece algo como isto:

$$

$$v_k = G_k (I_k ^ 1, w (I_k ^ 2, u (V_ {k-1})), V_ {k-1})$$

Para obter o próprio fluxo óptico, basta adicionar o predicado de rede e o aumento do fluxo do nível anterior:

$$

$$V_k = u (V_ {k-1}) + v_k.$$

Para obter a verdade da terra para a rede nesse nível, precisamos fazer a operação oposta - subtrair o predicado do alvo (reduzido ao nível desejado) do nível anterior da pirâmide. Esquematicamente, fica assim:



A vantagem dessa abordagem é que podemos ensinar cada nível independentemente. Os autores iniciaram o treinamento a partir do nível 0, cada rede subseqüente foi inicializada com os parâmetros da anterior. Como todas as redes $$$G_i$resolve o problema muito mais simples do que o cálculo completo do fluxo óptico em uma imagem grande, os parâmetros podem ser reduzidos muito menos. Tanto que agora todo o conjunto pode caber em dispositivos móveis:



O conjunto em si é o seguinte (um exemplo de uma pirâmide de 3 níveis):



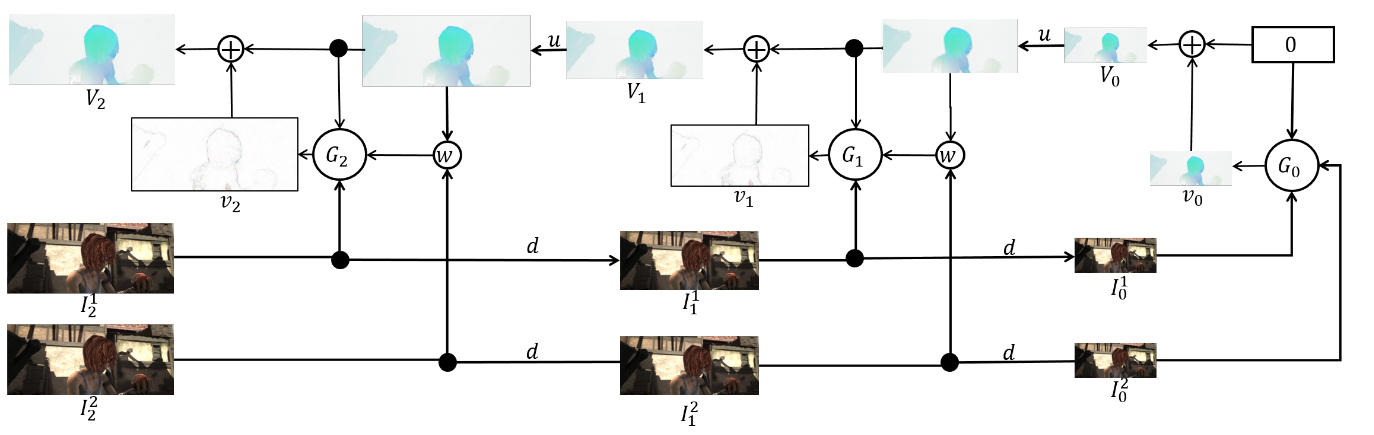
Resta falar diretamente sobre arquitetura $$$G_i$rede e faça um balanço. Toda rede $$$G_i$consiste em 5 camadas convolucionais, cada uma das quais termina com a ativação da ReLU, exceto a última (que prevê o fluxo óptico). O número de filtros em cada camada é respectivamente { $$ } As entradas da rede neural (a imagem, a segunda imagem “envolvida” no fluxo óptico e o próprio fluxo óptico) simplesmente concatenam de acordo com a dimensão dos canais, de modo que seu tensor de entrada possui 8. Os resultados são impressionantes:

PWC-Net (2018)

Inspirados pelo sucesso de seus colegas alemães, os funcionários da NVIDIA decidiram aplicar sua experiência (e placas de vídeo) para melhorar ainda mais o resultado. O trabalho deles foi amplamente baseado nas idéias do modelo anterior (SpyNet); portanto, a PWC-Net também lidará com pirâmides, mas com pirâmides de convolução, e não as imagens originais, no entanto, novamente - em ordem.

O uso de intensidades brutas de pixels para calcular o fluxo óptico nem sempre é razoável, porque Uma mudança acentuada no brilho / contraste quebrará nossa suposição de que os pixels se movem de um quadro para o próximo sem alterações e o algoritmo não será resistente a essas alterações. Nos algoritmos clássicos para o cálculo do fluxo óptico, são utilizadas várias transformações que atenuam essa situação. Nesse caso, os autores decidiram fornecer ao modelo a oportunidade de aprender elas mesmas. Portanto, em vez da pirâmide de imagem em PWC-Net, são usadas pirâmides de convolução (daí a primeira letra em Pwc-Net), ou seja, apenas apresentam mapas de diferentes camadas da CNN, que são chamados de extrator de pirâmide de recursos aqui.

Então tudo é quase como no SpyNet, pouco antes de você enviar para a CNN, que é chamada estimador de fluxo óptico, tudo que você precisa, a saber:

• imagem (neste caso, um mapa de características do extrator de pirâmide de características),
• o fluxo óptico amostrado calculado no nível anterior,
• a segunda imagem, "empacotada" (lembre-se da camada de deformação, daí a segunda letra em pWc-Net) nesse fluxo óptico,

entre o segundo quadro “embrulhado” e o primeiro habitual (mais uma vez, lembro que, em vez de imagens não processadas, cartões de recursos com extrator de pirâmide de recursos são usados ​​aqui) considere o que é chamado de volume de custo (daí a terceira letra no pwC-Net) e que já é essencialmente anteriormente considerada correlação entre duas imagens.



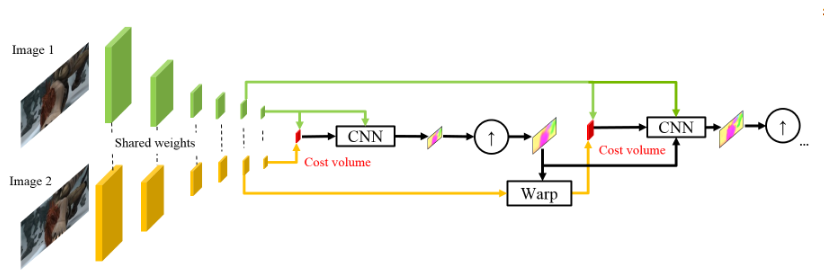
O toque final é a rede de contexto, que é adicionada imediatamente após o estimador de fluxo óptico e desempenha o papel de pós-processamento treinado para o fluxo óptico calculado. Detalhes arquitetônicos podem ser vistos no spoiler ou no artigo original.


Os resultados são ainda mais impressionantes:



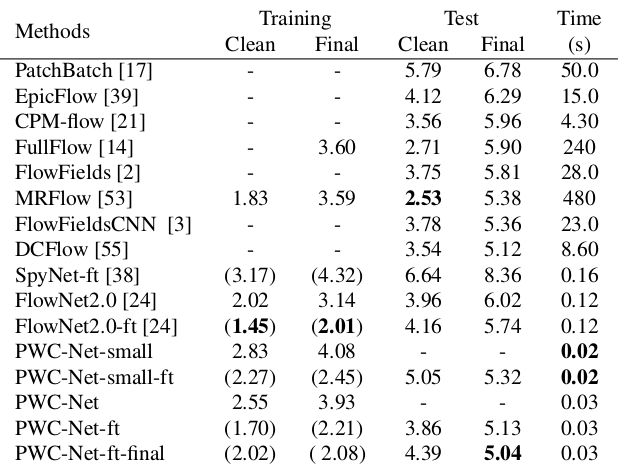
Comparado a outros métodos da CNN para calcular o fluxo óptico, o PWC-Net alcança um equilíbrio entre qualidade e número de parâmetros:



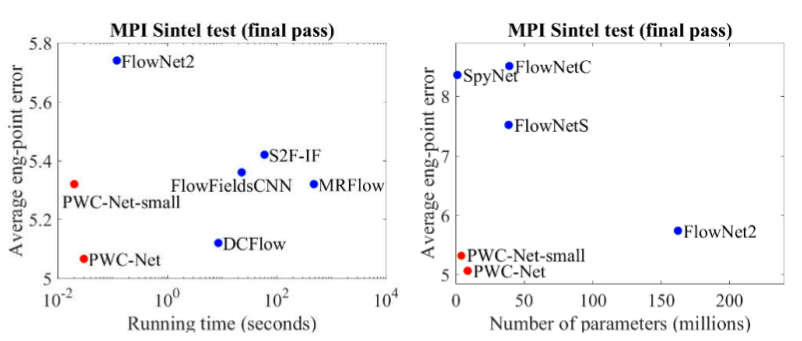
Há também uma excelente apresentação pelos próprios autores, na qual eles falam sobre o modelo em si e seus experimentos:

Conclusão

A evolução das arquiteturas que resolvem o problema da contagem de fluxo óptico é um exemplo maravilhoso de como o progresso nas arquiteturas da CNN e sua combinação com métodos clássicos fornece o melhor e o melhor resultado. E enquanto os métodos clássicos de CV ainda ganham qualidade, resultados recentes dão esperança de que isso seja corrigível ...

Fontes e links

1. FlowNet: Aprendendo o fluxo óptico com redes convolucionais: artigo , código .
2. Fluxo óptico de grande deslocamento: correspondência do descritor na estimativa de movimento variacional: artigo .
3. Estimativa de fluxo óptico usando uma rede de pirâmide espacial: artigo , código .
4. PWC-Net: CNNs para fluxo óptico usando pirâmide, distorção e volume de custos: artigo , código .
5. O que você queria saber sobre o fluxo óptico, mas teve vergonha de perguntar: artigo .
6. Cálculo do fluxo óptico pelo método Lucas-Canadá. Teoria: artigo .
7. Modelo correspondente ao OpenCVP: dock .
8. Quo Vadis, reconhecimento de ação? Um novo modelo e o conjunto de dados Kinetics: artigo .
9. FlowNet 2.0: Evolução da estimativa de fluxo óptico com redes profundas: artigo , código .