🍾 👳🏿 🏅 Quase o canal MIMO mais fácil com desbotamento (modelo Kronecker incluído) 🎧 ⛰️ 👨‍🚒

Bom dia a todos!

Considerando o tema da diversidade espacial , já abordamos as questões do desbotamento nos canais de comunicação e por que esse desbotamento ocorre. Hoje proponho falar sobre esse tópico com mais detalhes.

Além disso, no artigo de hoje, abordaremos levemente as questões de correlação espacial dos canais MIMO, que são tradicionalmente discutidas no curso do curso de comunicações móveis ( CSP ) do professor Haardt e, portanto, na minha opinião, essa publicação não será supérflua. E, notei imediatamente, que a variedade de problemas não se limita ao uso apenas em comunicações móveis.

Em geral, convido todos os interessados no assunto das comunicações sem fio a ler, e vamos lá!

Colin Slater "Memórias desaparecendo" . Sim, reduzir tudo a um tópico provavelmente é um exagero, mas com essa metáfora, acho que você pode imaginar o que o receptor recebe depois de todos os tipos de influências no sinal de informação original ...

Do que estamos falando?

Vamos começar com o fato de que na natureza existem os chamados ruídos multiplicativos que afetam a potência do sinal recebido - diminuindo .

Os termos, como você deve ter adivinhado, não são traduzidos diretamente em russo e inglês, mas isso não é muito importante.

Na literatura inglesa, o termo desbotamento implica uma certa influência que, por assim dizer, faz com que nosso sinal desapareça, "desapareça".

Em nossa literatura, o termo desbotamento é geralmente usado, e isso se deve principalmente ao efeito de caminhos múltiplos: se uma onda eletromagnética encontra sua cópia gerada por reflexos e difração e estão na fase antifásica, as ondas se cancelam umas às outras - ou seja, o canal , por assim dizer, congela .

O desbotamento é rápido e lento (desbotamento rápido e lento ).

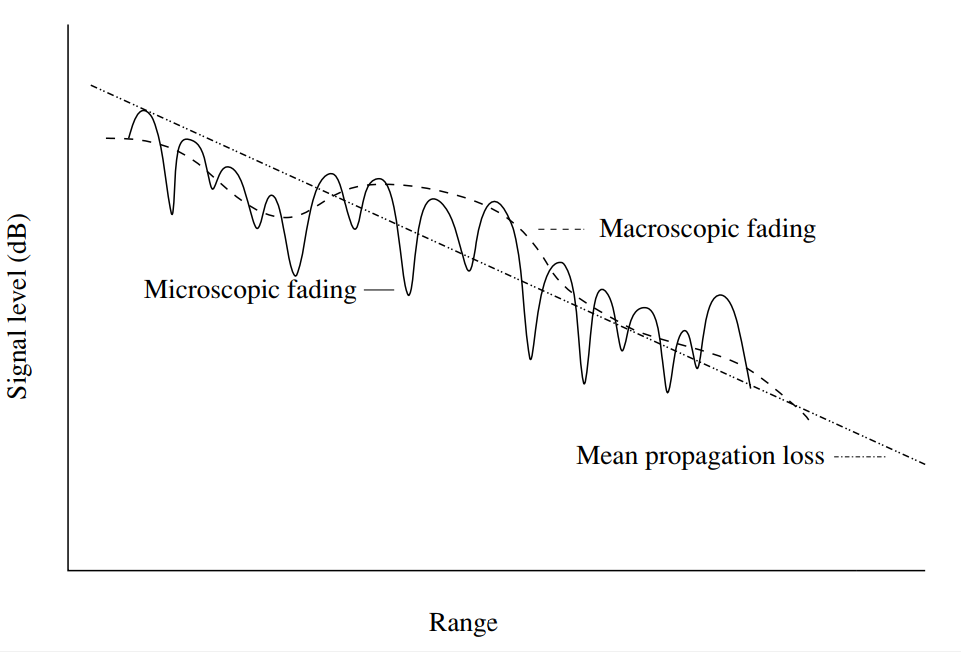
Fig. 1. Flutuações na potência do sinal nos canais sem fio, dependendo da distância. O nível médio de perda de propagação aumenta monotonamente com o aumento do alcance. Desvios locais podem ocorrer devido ao desbotamento macroscópico (lento) e microscópico (rápido) [1, p.14].

Confesso imediatamente, hoje não trabalharemos com desbotamento lento, mas falaremos sobre os rápidos com detalhes suficientes.

Fig. 2. Ilustração do efeito de sombreamento: como regra geral, ocorre o desbotamento lento devido ao sombreamento (sombreamento). Para simulação, a distribuição lognormal é geralmente escolhida.

Se você quiser ler um pouco sobre o desbotamento lento, em particular, e sobre como simular canais de satélite, em geral, convido você aqui !

Desvanecimento rápido

O desbotamento rápido ocorre, por regra, por dois motivos principais:

devido à propagação de caminhos múltiplos já mencionamos e / ou
devido a mudanças de frequência Doppler .

Estes últimos são muito perceptíveis para os sistemas de satélite , mas nem sempre são levados em consideração nos casos de comunicações terrestres, devido ao fato de que as estações base neste caso são geralmente estacionárias.

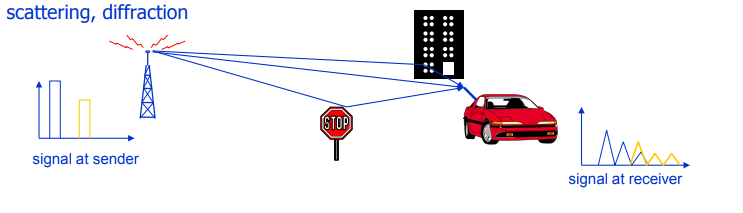
Fig. 3. Ilustração das causas do desbotamento. É dada atenção especial à dispersão e difração: é precisamente devido a esses fenômenos que a chamada propagação de caminhos múltiplos é formada, levando à interferência intersimbólica ( ISI ).

Mas isso está longe de tudo.

Desvanecimento seletivo vs. Desvanecimento plano

Acima, dividimos nossa interferência pela natureza da ocorrência . No entanto, a interferência também pode ser dividida pela natureza do efeito no sinal transmitido . E aqui precisamos do conceito de seletividade de canal.

Damos uma pequena classificação de acordo com [1, p. 14-18]. Portanto, o desbotamento rápido pode ser:

Seletiva
a. Frequência seletiva
b. Seleção de tempo
c. Espacialmente seletivo (refere-se à questão dos ângulos de chegada e partida das ondas EM - hoje não analisaremos essa questão)
Plano - gravitando mais em direção à natureza do desbotamento lento (sim, isso é um paradoxo)

O que o último termo implica é explicado pelo contrário.

Primeiro, se a largura do espectro do sinal transmitido por nós exceder a largura de banda coerente do canal , eles dizem que estamos lidando com interferências seletivas de frequência.

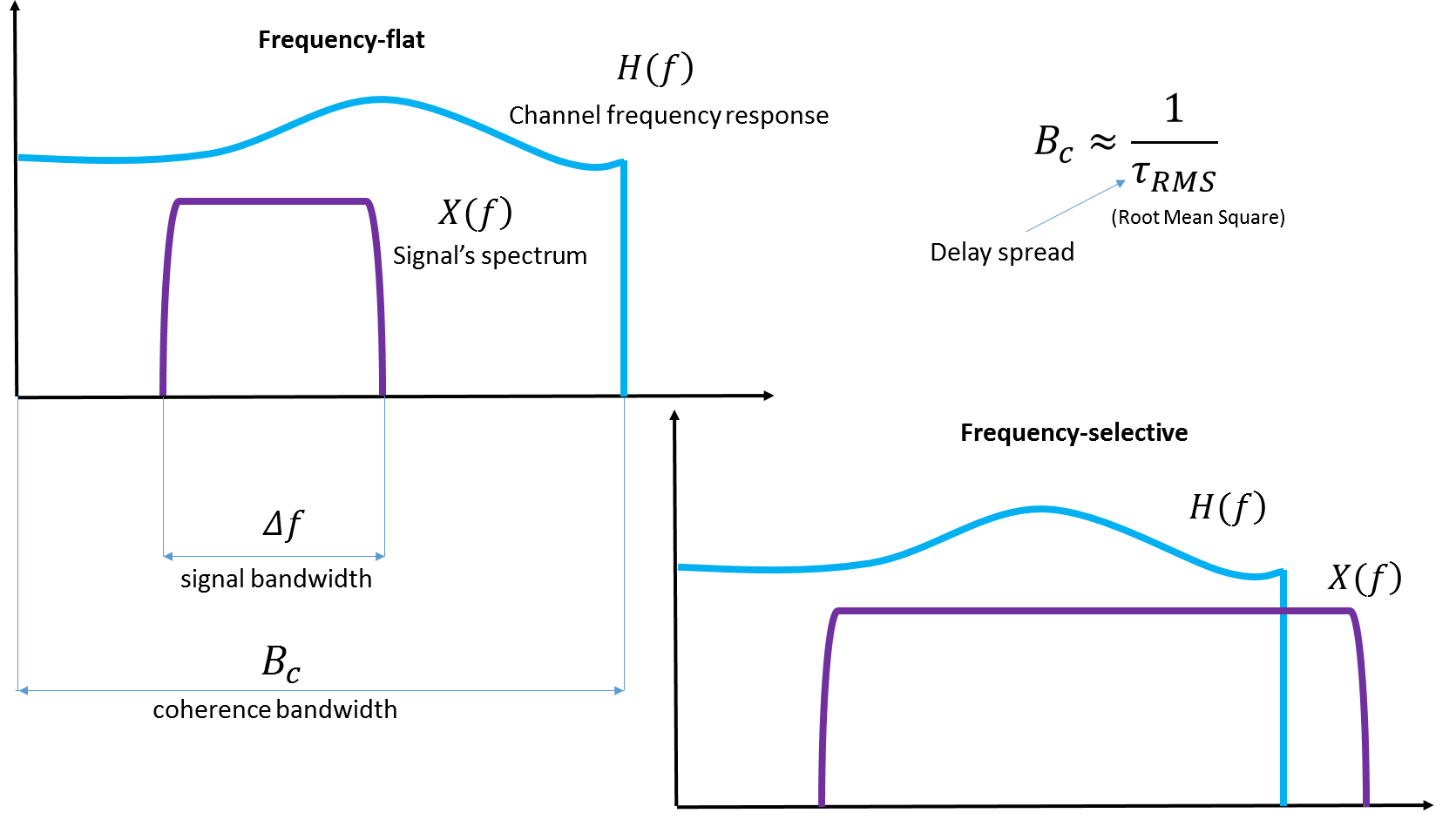
Fig. 4. Ilustração da largura de banda coerente. Eu acho que não será uma má idéia anexar ilustrações do Wiki , se ele as tiver adicionado lá.

Preste atenção à variável Atraso na propagação - a propagação de atrasos. É essa propagação de atrasos entre a chegada de cópias diferentes do mesmo sinal que é medida quando as características de um determinado canal real são determinadas.

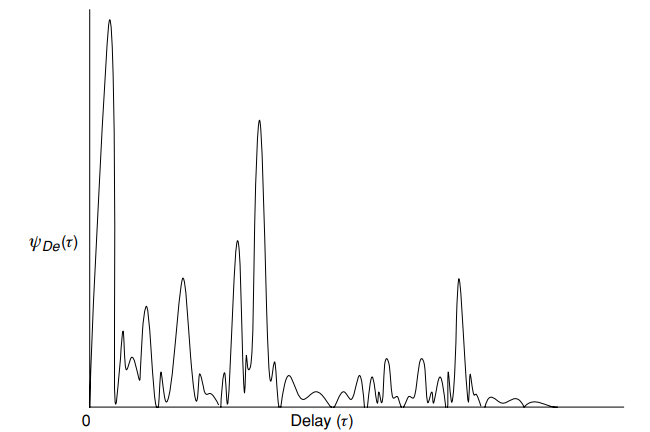
Fig. 5. Perfil típico de atraso (potência) $\ psi_ {De} (\ tau)$ - potência média em função do atraso $\ tau$ [1, p. 16]

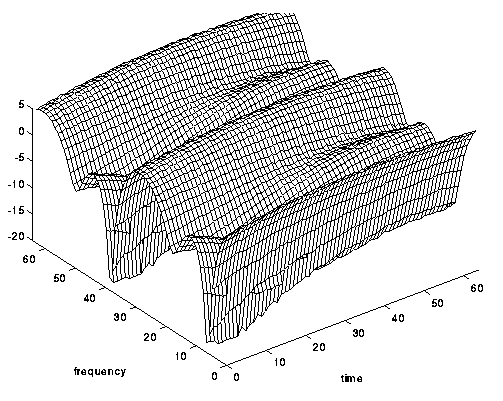
Fig. 6. Canal seletivo de frequência, mas não de tempo .

Para cada faixa, a banda coerente será diferente.

Por exemplo, para a banda S (eu estava interessado quando procurava informações sobre sistemas de satélite) Bc = 0,5 - 2 MHz (Kanatas AG, Panagopoulos AD (ed.). Propagação de ondas de rádio e modelagem de canais para sistemas espaciais e terrestres. - CRC Press, 2016 107).

Isso se encaixa muito bem na taxa de transmissão de , por exemplo, um transceptor de satélite . E não há nada de surpreendente: a taxa de símbolos dos tipos lineares de modulação digital (PSK, QAM, OFDM) coincide com a banda ocupada pelo sinal (ver Goldsmith A. Wireless Communications . - Stanford University, 2004. - p. 140, 326), o que significa seria bom tentar espremer o sinal na banda coerente ao máximo. As frequências ainda são um recurso valioso.

Em segundo lugar, se a duração do nosso sinal no domínio do tempo exceder o tempo de coerência do canal , eles dizem que estamos lidando com um canal que varia no tempo.

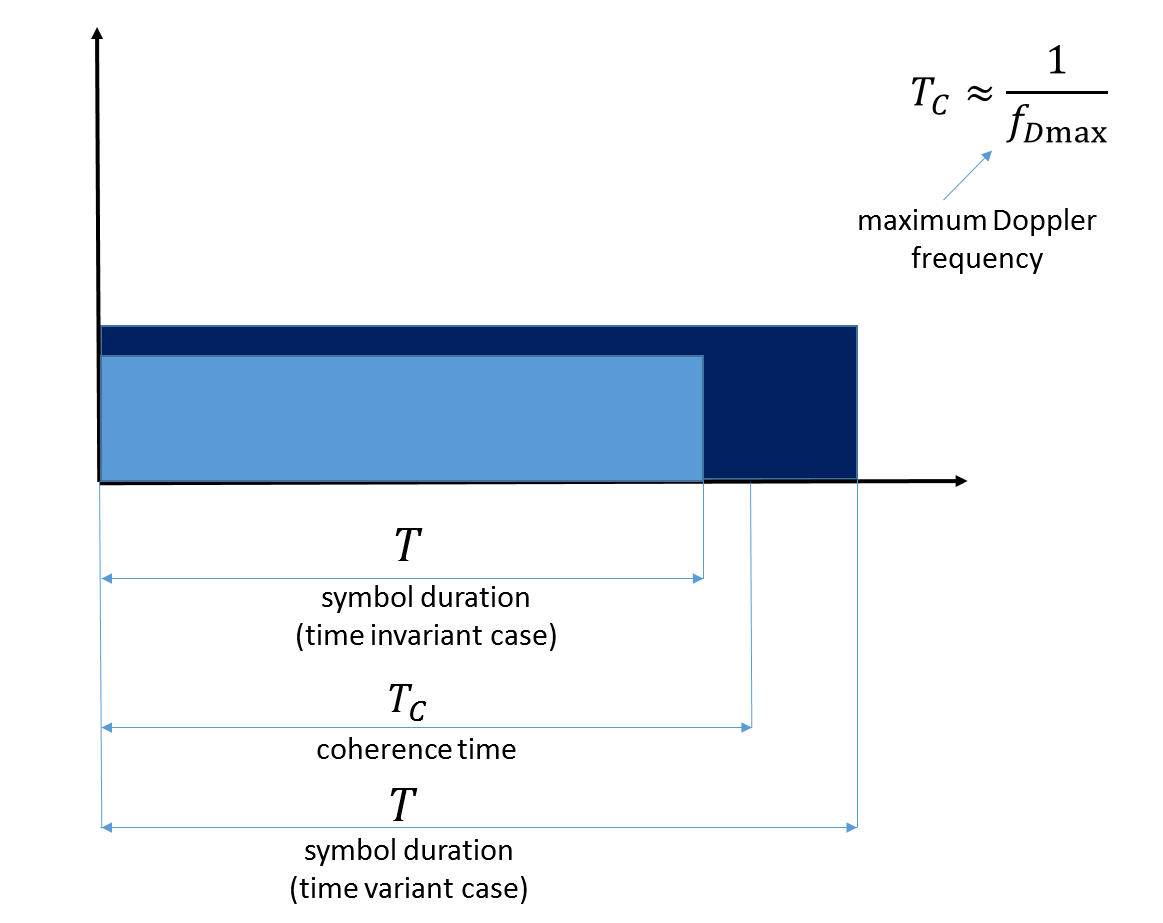
Fig. 7. Ilustração do tempo de coerência. Observe que aqui a frequência máxima do Doppler reflete o movimento do próprio terminal móvel.

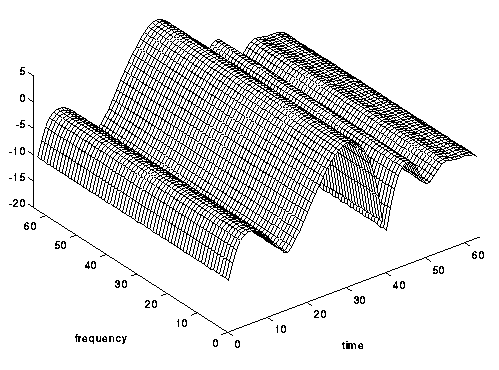
Fig. 8. Quase invisível no tempo, mas seletivo no tempo: um canal em rápida decomposição.

Na vida real, infelizmente, é preciso esperar ambos.

Canal Rayleigh com seleção de tempo e de frequência; "A situação real."

Fonte da ilustração: Tecnologia sem fio Gigabit

Bem, e consequentemente, se conseguirmos evitar de alguma forma o acima exposto, chegaremos ao caso mais simples e conveniente - desbotamento achatado [1, p. 14-18] [2, p. 88-92].

O canal de desbotamento mais fácil

Você já deve ter visto uma maneira semelhante de simular um canal plano com desvanecimento em algum lugar:

h = (1/sqrt(2))*(randn(size(msg)) + 1j*randn(size(msg))) % MatLab / Octave

O que se entende:

falta de linha de visão (um caso justificado para comunicações terrestres)
canal de banda estreita (canal de banda estreita) - encaixe na banda coerente
- A propósito, consideramos um exemplo de canal de banda larga neste artigo (Fig. 4).
também não há seletividade de frequência - cabe no tempo coerente
falta de sombreamento e mudanças de frequência Doppler

Ou seja, aqui está pessoalmente: um canal plano com desbotamento . Para um caso sem linha de visão, o canal também é chamado Rayleigh .

Lord Rayleigh

De que vem esse modelo?

Primeiro, falando sobre sistemas de comunicação modernos, provavelmente queremos dizer trabalhar com sinais digitais. Além disso, também estamos trabalhando provavelmente com tipos de modulação em quadratura ( I / Q ), ou seja, com sinais complexos.

Fig. 9. A constelação de sinal QPSK . Coordenadas polares, círculo unitário. Por exemplo, o símbolo 11 corresponderá a uma coordenada igual a aproximadamente 0,7 + 0,7i .

É lógico assumir o efeito da interferência no componente real e no imaginário. Além disso, vale a pena seguir o Teorema do Limite Central para assumir também a natureza gaussiana de tais efeitos. Escrevemos a fórmula [1, p. 39]:

$Z = X + jY \ qquad (1)$

onde $X \ sim \ mathcal {N} (0, \, \ sigma ^ 2)$ e $Y \ sim \ mathcal {N} (0, \, \ sigma ^ 2)$ São variáveis aleatórias normalmente distribuídas.

Na maioria das vezes, um modelo com uma potência média normalizada é usado:

$var \ {Z \} = E \ {\ left | Z \ right | ^ 2 \} = 1 \ qquad (2)$

E isso significa $Z \ sim \ mathcal {N} (0, \, 1)$ .

Se assumirmos distorções independentes dos componentes do envelope de sinal: em fase ( I - Em fase) e em quadratura ( Q - Quadratura), então a posição do número pelo qual o símbolo original será multiplicado (daí o ruído multiplicativo ), nas coordenadas polares pode ser calculado literalmente pelo teorema de Pitágoras:

$Z = \ sqrt {\ hat {X} ^ 2 + \ hat {Y} ^ 2} \ qquad (3)$

onde $\ hat {X} \ sim \ mathcal {N} (0, \, \ sigma ^ 2)$ e $\ hat {Y} \ sim \ mathcal {N} (0, \, \ sigma ^ 2)$ - estas também são variáveis aleatórias normalmente distribuídas. Para potência nominal $\ hat {X} \ sim \ mathcal {N} (0, \, 1)$ , $\ hat {Y} \ sim \ mathcal {N} (0, \, 1)$ .

E aqui temos a fórmula do processo Rayleigh ! [2, p. 78]

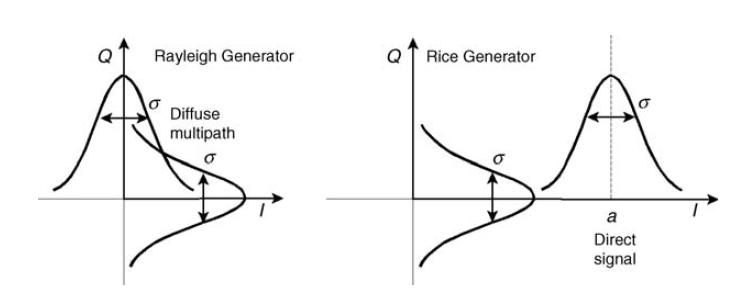
Fig. 10. Geradores quadrados gaussianos para modelar o desbotamento de Rayleigh e Rice [3, p.125]. Falaremos sobre o canal Rice um pouco mais tarde.

Digressão lírica.

Pessoalmente, eu realmente gosto do exemplo de mira : se duas armas disparam perpendiculares uma à outra um número suficiente de vezes, então para cada uma individualmente a distribuição de acertos será normal e a distribuição total de acertos é Rayleigh. Algo semelhante está acontecendo com a nossa interferência.

Se considerarmos o caso mais simples sem nenhuma correlação espacial entre os canais (digamos que temos vários canais espaciais - MIMO ), eles dizem que o canal é espacialmente branco - espacialmente branco . E, como todos os canais são independentes, é possível “gerar” não apenas variáveis aleatórias distribuídas de acordo com Rayleigh, mas também vetores, matrizes e tensores [3, p. 125]:

$\ mathbf {H} _ {NLoS} = \ sqrt {\ frac {1} {2}} \ left (\ mathbf {G} _1 + j \ mathbf {G} _2 \ right) \ qquad (4)$

onde $\ mathbf {G} _1 \ sim \ mathcal {N} (0, \, 1)$ e $\ mathbf {G} _2 \ sim \ mathcal {N} (0, \, 1)$ São matrizes que consistem em valores normalmente distribuídos.

De onde veio 1/2 sob a raiz?

Tudo é bem simples aqui: como dissemos acima, o poder de resposta do canal deve ser igual à unidade, ou seja:

$P = E \ {hh ^ * \} = 1$

É por isso que o fator de escala é introduzido $\ sqrt {\ frac {1} {2}}$ .

Demonstre (use o python para variar):

 import numpy as np N = int(1e6) h = 1/np.sqrt(2)*(np.random.randn(N) + 1j*np.random.randn(N)) P = np.mean(h*np.conj(h)) print(np.round(P)) >>> (1+0j)

Para resumir :
O componente de interferência na ausência de visibilidade direta pode ser descrito como um vetor n-dimensional (dependendo da dimensão do canal) independente distribuído identicamente ( IID - independente distribuído identicamente) de acordo com a lei gaussiana complexa com simetria circular e tapete zero. números de expectativa ( ZMCSCG - Gaussiano complexo circularmente simétrico com média zero).

Um trava-língua inteiro!

Quase o canal de desbotamento mais fácil

Bem, e se ainda houver visibilidade direta? Talvez já existam modelos matemáticos prontos para esse resultado?

Claro que sim! Por exemplo, isso [4] , generalizado para o caso com várias antenas de recepção e transmissão (MIMO):

$\ mathbf {H} = \ sqrt {\ frac {K} {K + 1}} \ mathbf {H_ {LoS}} + \ sqrt {\ frac {1} {K + 1}} \ mathbf {H_ {NLoS} } \ qquad (5)$

onde $$ \ mathbf {H}$ - este é realmente o complexo envelope da resposta ao impulso do canal (ou matriz do canal, se estamos falando sobre MIMO ), $$ \ mathbf {H_ {LoS}}$ É um componente da visibilidade direta (linha de visão) e $\ mathbf {H_ {NLoS}}$ - este é um componente da falta de visibilidade direta (fora da linha de visão), já o consideramos.

Preste atenção à variável K - este é o chamado fator Rice (fator riciano / ricino) - a razão entre a potência do caminho de propagação direta e a potência de todos os outros caminhos. É ele quem determina quanto nosso canal estará sujeito a interferências.

Stephen O. "Steve" Rice

Prazo $\ sqrt {\ frac {K} {K + 1}} \ mathbf {H} _ {LoS} = E \ {H \}$ representa a expectativa matemática da matriz de canais e pode ser modelado com base na geometria das matrizes de recepção e transmissão de antenas:

$\ mathbf {H} _ {LoS} = \ mathbf {a} _R (\ theta_R) \ mathbf {a} _T (\ theta_T) ^ H \ qquad (6)$

onde $\ mathbf {a} _R (\ theta_R)$ e $\ mathbf {a} _T (\ theta_T)$ - estas são as respostas das matrizes de recepção e transmissão de antenas, respectivamente, e $\ theta_R$ e $\ theta_T$ São os ângulos de chegada e partida (ângulo de partida).

Os fatores são geralmente simétricos e podem ser descritos pela fórmula geral:

$\ mathbf {a} = \ left [1, e ^ {j2 \ pi d cos (\ theta)}, ..., e ^ {j2 \ pi d (N-1) cos (\ theta)} \ right] \ qquad (7)$

onde $d$ A distância entre antenas (espaçamento da antena) em comprimentos de onda e $N$ - este é o número de elementos na matriz de antenas (Fig. 11).

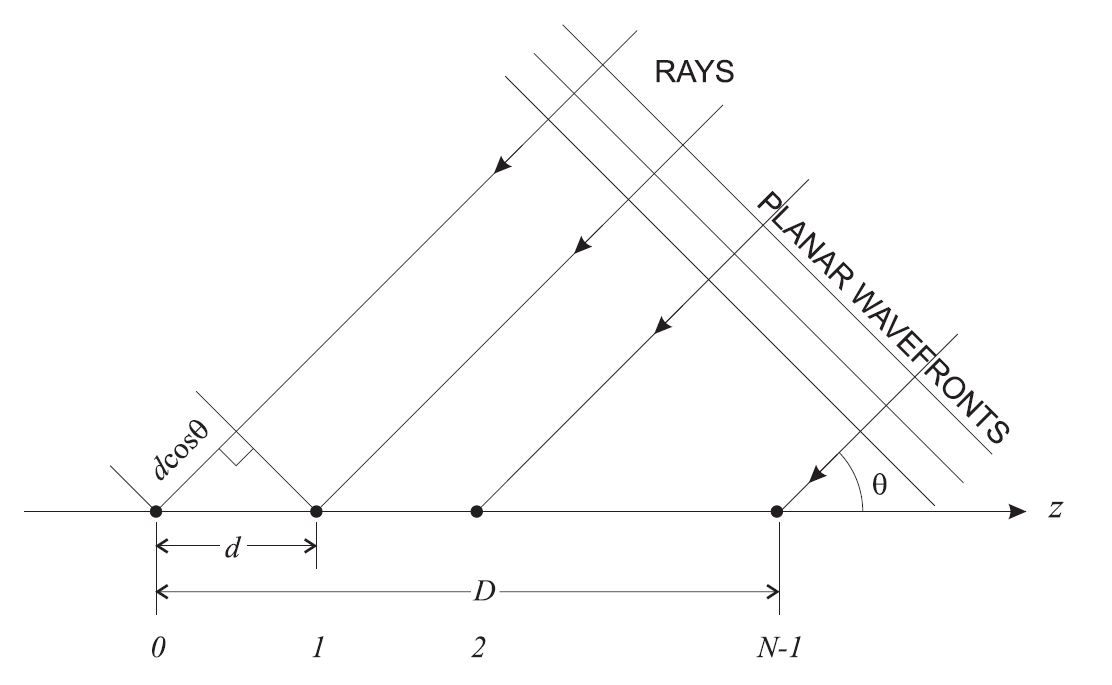
Fig. 11. A geometria de uma matriz linear . Para o MIMO maciço, a geometria, é claro, será diferente. Você pode ler mais sobre isso, por exemplo, aqui .

Bem, agora que o modelo está pelo menos um pouco desmontado, você pode simplificá-lo.

Para o caso do SISO (o mais simples e o mais básico), a fórmula (5) assumirá a forma:

$h = \ sqrt {\ frac {K} {K + 1}} + \ sqrt {\ frac {1} {2 (K + 1)}} \ left (G_1 + jG_2 \ right) \ qquad (8)$

para 1 antena transmissora e 1 antena receptora $\ mathbf {a} _T (\ theta_T) \ mathbf {a} _R (\ theta_R) = 1$ .

E isso, a propósito, se encaixa no modelo da Figura 12.

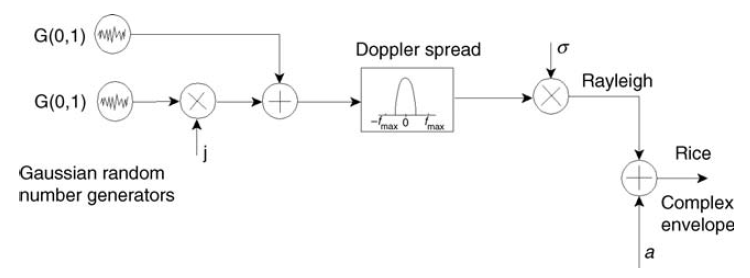
esquema

Fig. 12. O esquema de formação do canal de Rice (sinal de banda estreita) [3, p.127]. At $K \ to 0$ o canal degenerará cada vez mais em Rayleigh. Foi por isso que usei a palavra quase na legenda: o canal Rayleigh é um caso especial do canal Rice. Isso também é visto na fórmula (5).

Vamos explicar: $\ sigma = \ sqrt {\ frac {1} {2 (K + 1)}}$ O parâmetro da escala riciana e $a = \ sqrt {\ frac {K} {K + 1}}$ É um parâmetro de não centralidade.

Se considerarmos o desbotamento plano, presume-se que o bloco Doppler Spread tenha uma resposta de 1.

Em geral, com a finalidade de modelar o Doppler Spread, provavelmente você encontrará um modelo de Jakes (em forma de U) baseado na técnica da soma dos sinusóides . Teoricamente, o espectro desse modelo se parece com o seguinte:

A densidade espectral de potência da atenuação de Rayleigh com um desvio Doppler máximo de 10 Hz. Fonte

No entanto, na vida, a julgar por [1, p. 15] esse espectro ainda parece menos uniforme:

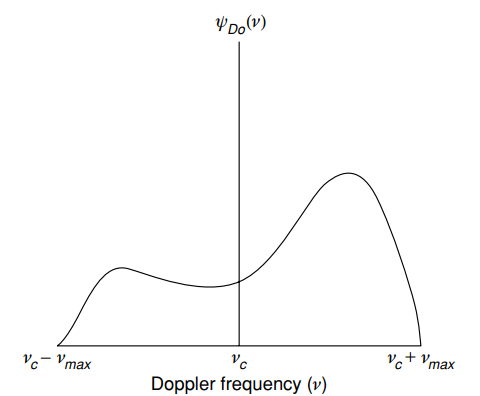
Espectro típico de Doppler (energia) $\ psi_ {Faça} (v)$ - potência média em função da frequência Doppler $(v)$ [1, p. 15]

Expectativas ... Realidade.

Existem tais esquemas para combinar com desbotamento lento.

Por exemplo, isso é para o modelo Corazza-Vatalaro (C & V) :

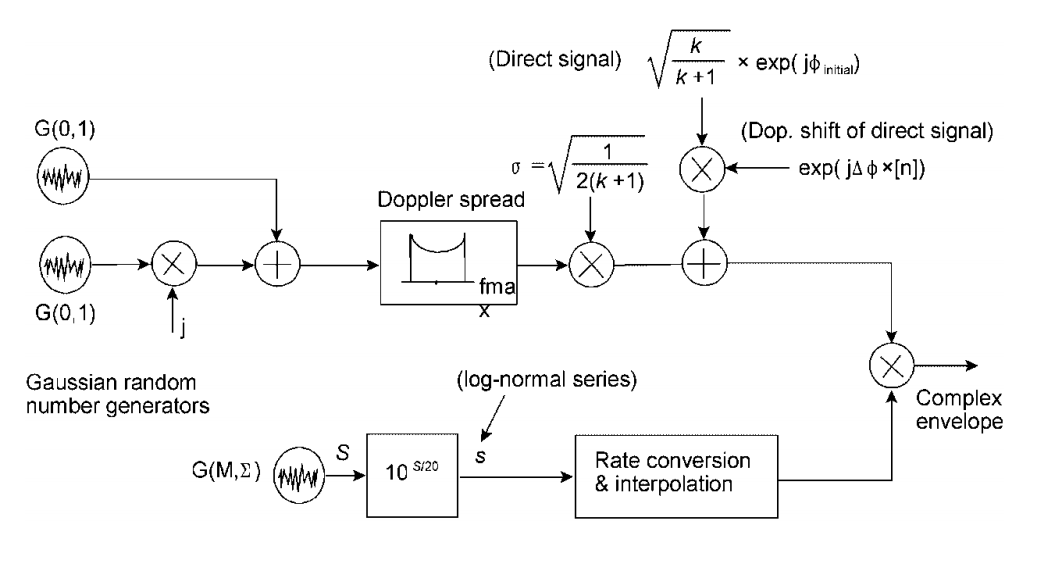
ver Fontan, FP, Mayo, A., Marote, D., Prieto - Cerdeira, R., Mariño, P., Machado, F. e Riera, N. (2008). Revisão de modelos generativos para o canal móvel de propagação de satélite terrestre em banda estreita. International Journal of Satellite Communications and Networking, 26 (4), 291-316.

Mas esta é uma história completamente diferente ...

Modelando quase o canal de desbotamento mais fácil do MatLab

Vamos comparar os cálculos recebidos com algo já verificado. Por exemplo, com funções especiais do MatLab .

Para testar o modelo, por nossa parte, geramos uma mensagem binária aleatória (o tamanho da mensagem é de 100.000 bits), modula-a usando M-PSK ou M-QAM , multiplica elemento por elemento no processo de desbotamento, adiciona ruído gaussiano branco, equaliza o equalizador de força zero, desmodula e calcula taxa de erro de bit (BER - taxa de erro de bit) (Fig. 13). O número de testes será igual a cem.

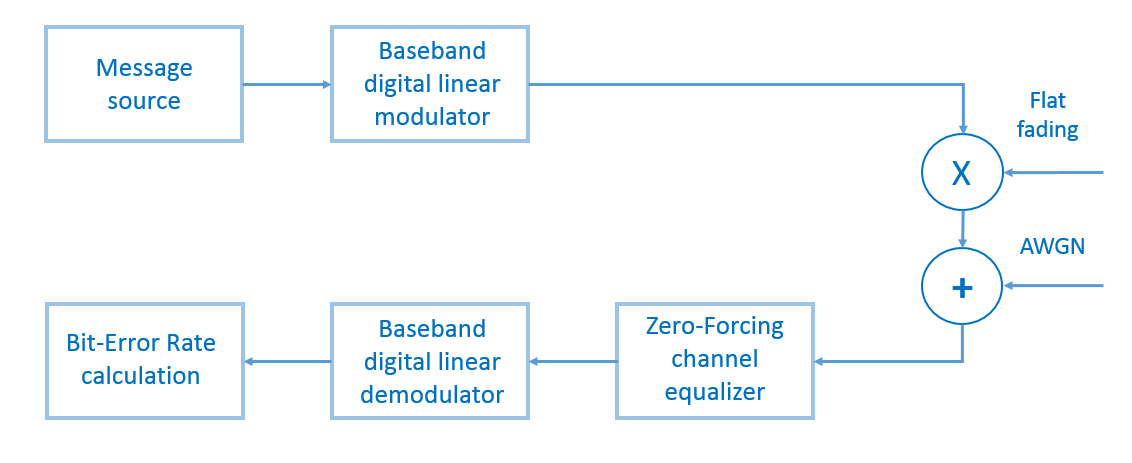
Fig. 13. O diagrama de blocos do modelo do sistema de transmissão que nosso script descreverá.

O script pode ser visto aqui.

E faça o download aqui .

 clear all; close all; clc EbNo = 0:40; K = [4.0; 0.6]; M = [4; 8; 16; 64; 256]; %Positions of modulation (M-PSK or M-QAM) for k = 1:length(K) for m = 1:length(M) message = randi([0, M(m)-1], 100000, 1); if M(m) >= 16 mod_msg = qammod(message, M(m), pi/4, 'gray'); ric_ber(:, m, k) = berfading(EbNo,'qam',M(m),1,K(k)); else mod_msg = pskmod(message, M(m), pi/4, 'gray'); ric_ber(:, m, k) = berfading(EbNo, 'psk', M(m), 1, K(k)); end Es = mean(abs(mod_msg).^2); No = Es./((10.^(EbNo./10))*log2(M(m))); h = sqrt( K(k)/(K(k)+1)) +... sqrt( 1/(K(k)+1))*(1/sqrt(2))*(randn(size(mod_msg))... + 1j*randn(size(mod_msg))); ric_msg = mod_msg.*h; % Rician flat fading for c = 1:100 for jj = 1:length(EbNo) noisy_mod = ric_msg +... sqrt(No(jj)/2)*(randn(size(mod_msg))+... 1j*randn(size(mod_msg))); %AWGN noisy_mod = noisy_mod ./ h; % zero-forcing equalization if M(m) >= 16 demod_msg = qamdemod(noisy_mod, M(m), pi/4, 'gray'); else demod_msg = pskdemod(noisy_mod, M(m), pi/4, 'gray'); end [number,BER(c,jj)] = biterr(message,demod_msg); end end sum_BER(:,m, k) = sum(BER)./c; end end figure(1) semilogy(EbNo, sum_BER(:,1,1), 'b-o', EbNo, sum_BER(:,2,1), 'r-o',... EbNo, sum_BER(:,3,1), 'g-o', EbNo, sum_BER(:,4,1), 'c-o',... EbNo, sum_BER(:,5,1), 'k-o',... EbNo, ric_ber(:,1,1), 'b-', EbNo, ric_ber(:,2,1), 'r-',... EbNo, ric_ber(:,3,1), 'g-', EbNo, ric_ber(:,4,1), 'c-',... EbNo, ric_ber(:,5,1), 'k-', 'LineWidth', 1.5) title('Rician model (K = 4.0)') legend('QPSK(simulated)', '8-PSK(simulated)',... '16-QAM(simulated)', '64-QAM(simulated)' ,'256-QAM(simulated)',... 'QPSK(theory)','8-PSK(theory)', '16-QAM(theory)',... '64-QAM(theory)' ,'256-QAM(theory)','location','best') xlabel('EbNo (dB)') ylabel('BER') grid on figure(2) semilogy(EbNo, sum_BER(:,1,2), 'b-o', EbNo, sum_BER(:,2,2), 'r-o',... EbNo, sum_BER(:,3,2), 'g-o', EbNo, sum_BER(:,4,2), 'c-o',... EbNo, sum_BER(:,5,2), 'k-o',... EbNo, ric_ber(:,1,2), 'b-', EbNo, ric_ber(:,2,2), 'r-',... EbNo, ric_ber(:,3,2), 'g-', EbNo,ric_ber(:,4,2), 'c-',... EbNo, ric_ber(:,5,2), 'k-','LineWidth', 1.5) title('Rician model (K = 0.6)') legend('QPSK(simulated)', '8-PSK(simulated)',... '16-QAM(simulated)', '64-QAM(simulated)' ,'256-QAM(simulated)',... 'QPSK(theory)','8-PSK(theory)',... '16-QAM(theory)', '64-QAM(theory)' ,'256-QAM(theory)','location','best') xlabel('EbNo (dB)') ylabel('BER') grid on

Você deve obter algo como isto:

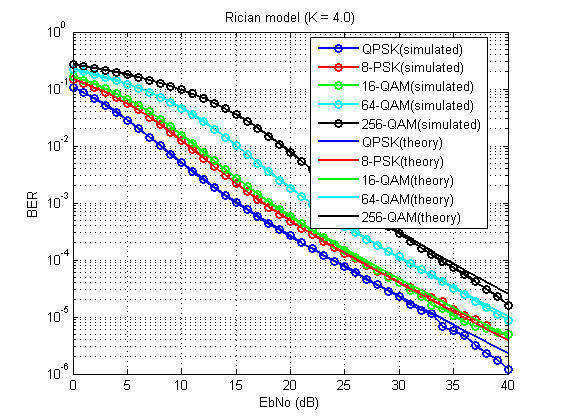
Fig. 14. O coeficiente de erros de bit para o modelo considerado (K = 4,0).

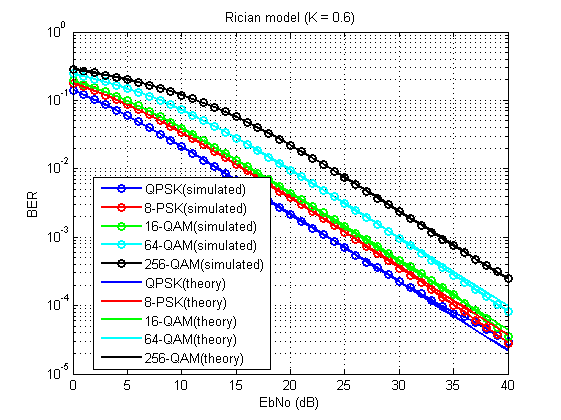
Fig. 15. Taxa de erro de bit para o modelo considerado (K = 0,6).

Não sem falhas, é claro (devido ao número limitado de médias), mas em geral, pode-se ver que funciona!

Ok, mas será possível dimensionar o experimento para o caso do MIMO? Sim claro.

Para fazer isso, fazemos uma suposição: a matriz do canal consistirá em caminhos de propagação independentes, cada um dos quais será distribuído de acordo com Rice.

Sob que condições isso é possível?

Como observamos acima, o IDI do componente pode ser gerado em qualquer dimensão. Isso significa que qualquer canal MIMO espacialmente branco sem linha de visão pode ser modelado como um conjunto de canais SISO (dependendo da dimensão do canal).

Com o componente da linha de visão um pouco mais complicado - você precisa levar em consideração a posição das grades.

Considere a fórmula (5): se nossa matriz do componente da linha de visão consistir apenas em unidades $\ mathbf {H} _ {LoS} = \ mathbf {1}$ , parece que o componente Raysov também se torna espacialmente branco.

Para abordar isso, escrevemos o componente da linha de visão com mais detalhes do que na fórmula (6):

$\ mathbf {H} _ {LoS} = \ begin {bmatrix} 1 \\ \ exp (j2 \ pi dcos (\ theta_R)) \\. \\. \\. \\ \ exp (j (M_R-1) 2 \ pi dcos (\ theta_R)) \ end {bmatrix} \ begin {bmatrix} 1 & \ exp (j2 \ pi dcos (\ theta_T)) &. &. &. & \ exp (j (M_T-1) 2 \ pi dcos (\ theta_T)) \ end {bmatrix}$

É impressionante que se $\ theta_R = \ theta_T = 90 ^ o$ , a matriz consistirá em uma unidade. Geometricamente, é uma situação em que duas matrizes de elementos são orientadas estritamente uma na outra:

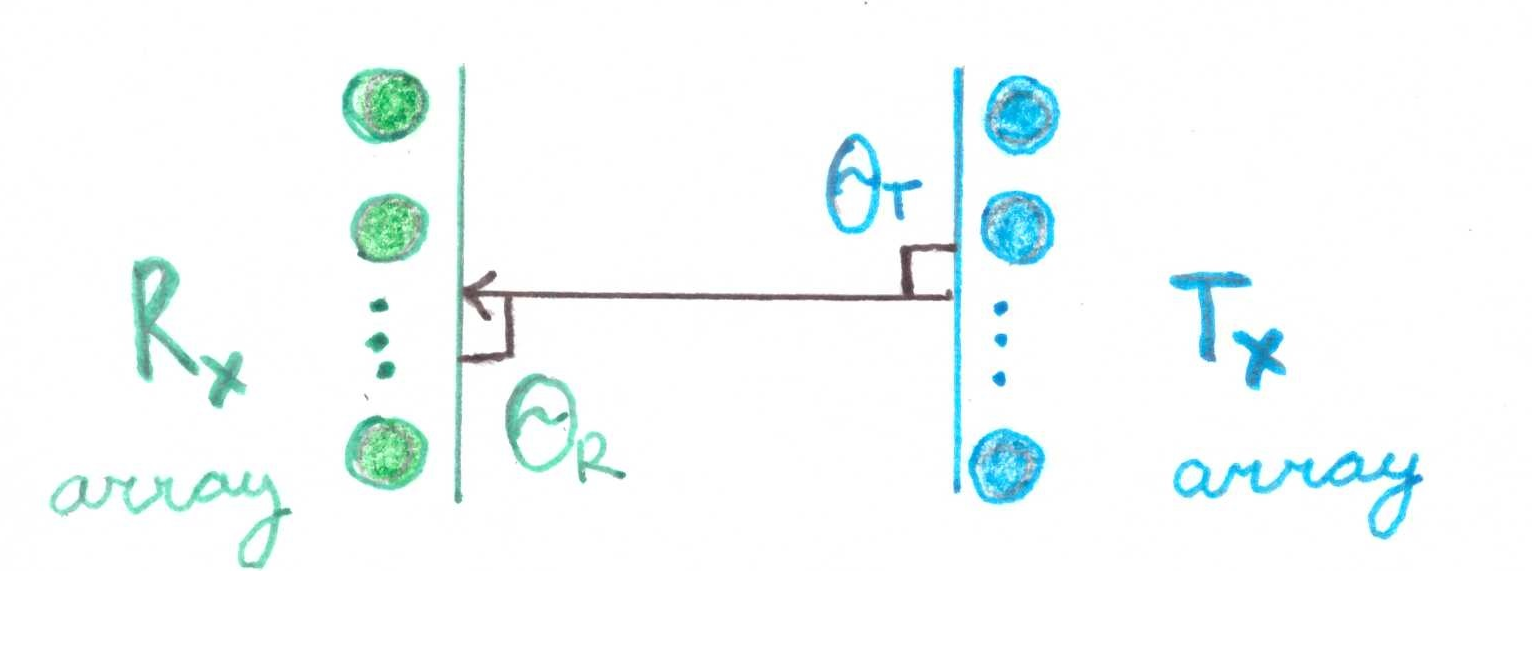
Vamos fazer uma pequena demonstração matemática:

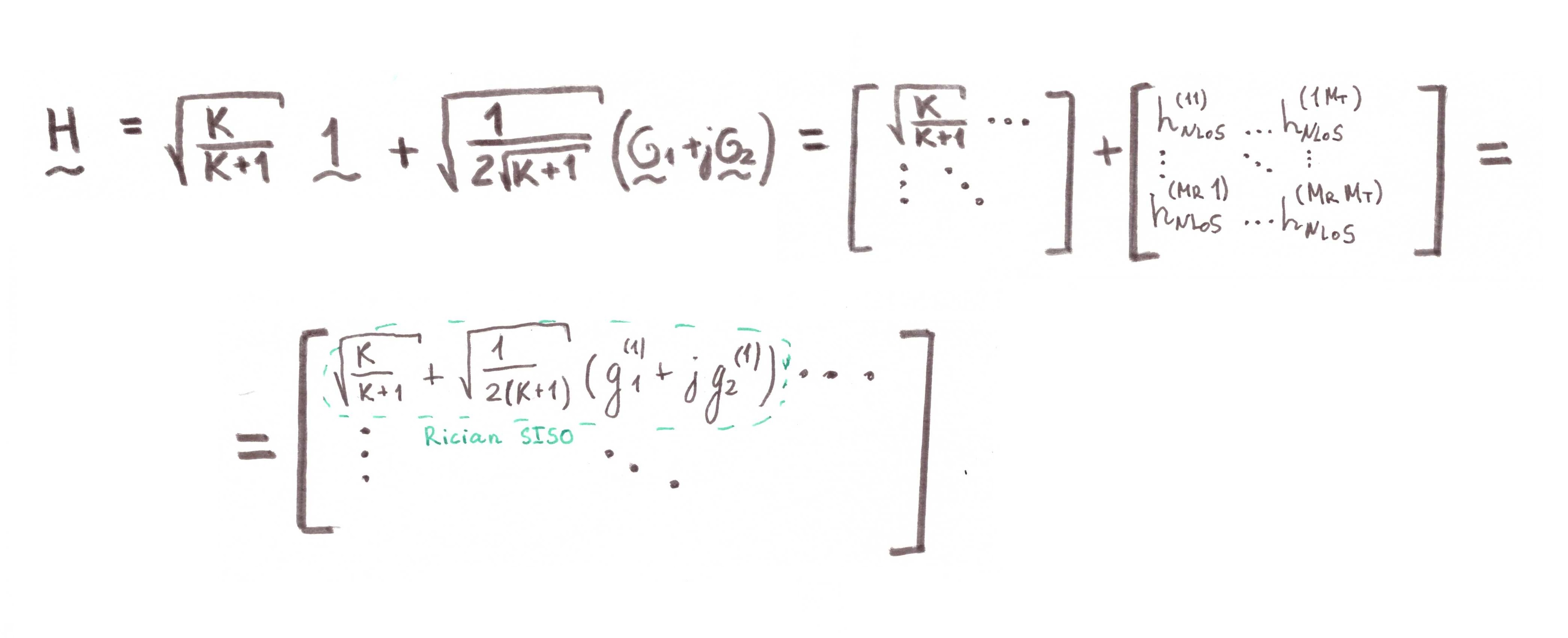
Para modelagem, tomamos como base o esquema Alamouti . Deveria acontecer algo assim:

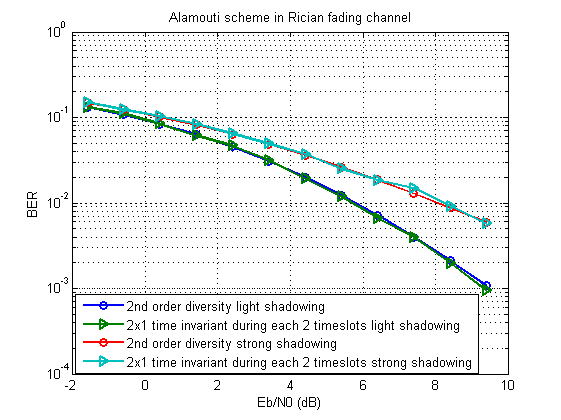
O script estendido pode ser baixado aqui .

Bem feito.

Quase o canal de desvanecimento mais fácil e a correlação espacial

E agora, concluindo nossa jornada no mundo dos cálculos estatísticos, vamos nos aproximar um pouco da realidade.

Acima, consideramos o caso em que o componente da falta de linha de visão era espacialmente branco . No entanto, em sistemas reais, ainda se deve esperar alguma correlação entre as antenas e, portanto, entre os caminhos de propagação da onda EM.

Introduzimos uma nova variável - a matriz de correlação espacial:

$\ mathbf {R} = E \ {vec (\ mathbf {H}) vec (\ mathbf {H}) ^ H \} \ qquad (8)$

onde vec denota uma operação de vetorização . A propósito, essa matriz afetará apenas o componente da falta de linha de visão e, portanto, neste caso $\ mathbf {H} = \ mathbf {H} _ {NLoS}$ .

Exemplo para MIMO 2x2

É razoável supor que, na vida real, essa matriz seja determinada primeiro por meio de medições e somente então elas serão usadas para modelagem:

$vec (\ mathbf {H} _ {NLoS}) = \ mathbf {R} ^ {1/2} vec (\ mathbf {H} _w) \ qquad (9)$

onde $\ mathbf {H} _w$ É a matriz do IID ( w significa espacialmente branco).

Observe que elevar uma matriz a uma potência não é elevar a uma potência de cada um de seus elementos. Portanto, no nosso caso, a função sqrt () não pode ser usada no MatLab . Use o operador ^ .
No caso do Python, você não pode usar o operador de exponenciação ** e o método sqrt do popular módulo numpy . Você precisa usar o método fractal_matrix_power do módulo scipy .

Se o receptor e o transmissor forem suficientemente independentes um do outro, como na Figura 16, o modelo Kronecker poderá ser aplicado [1, p. 40], para reduzir o número de coeficientes de cálculo:

$\ mathbf {R} = \ mathbf {R} ^ T_T \ otimes \ mathbf {R} _R \ qquad (10)$

onde $\ otimes$ denota um trabalho Kronecker .

Leopold Kronecker

Consideramos separadamente os componentes da matriz de expressão:

$\ mathbf {R} _R = \ frac {1} {M_T} E \ left \ {\ left (\ mathbf {H} _ {NLoS} \ mathbf {H} ^ H_ {NLoS} \ right) ^ T \ right \ }$ É a matriz de correlação das antenas receptoras,

$\ mathbf {R} _T = \ frac {1} {M_R} E \ left \ {\ mathbf {H} ^ H_ {NLoS} \ mathbf {H} _ {NLoS} \ right \}$ É a matriz de correlação das antenas de transmissão

$M_R$ e $M_T$ - este é o número de antenas de recepção e transmissão, respectivamente. Ambas as matrizes são matrizes hermitianas semi-definidas positivas. Além disso, a classificação da matriz $\ mathbf {H} _ {NLoS}$ limitado por valor $min (classificação (\ mathbf {R} _T), classificação (\ mathbf {R} _R))$ .

Fig. 16
Modelo de difusores no caso de receptor e transmissor não correlacionados. Pontos verdes significam difusores, receptor e transmissor azuis e vermelhos. Peço desculpas pela qualidade, esta é uma captura de tela de um dos trabalhos de casa de TU Ilmenau.

A matriz do canal, neste caso, pode ser escrita como:

$\ mathbf {H} = \ sqrt {\ frac {K} {K + 1}} \ mathbf {H} _ {LoS} + \ sqrt {\ frac {1} {K + 1}} \ mathbf {R} ^ {1/2} _R \ mathbf {H} _ {w} \ left (\ mathbf {R} ^ {1/2} _T \ right) ^ H \ qquad (11)$

No entanto, para situações como, por exemplo, na Figura 17, você ainda precisa usar a matriz de correlação completa (consulte a fórmula (9)).

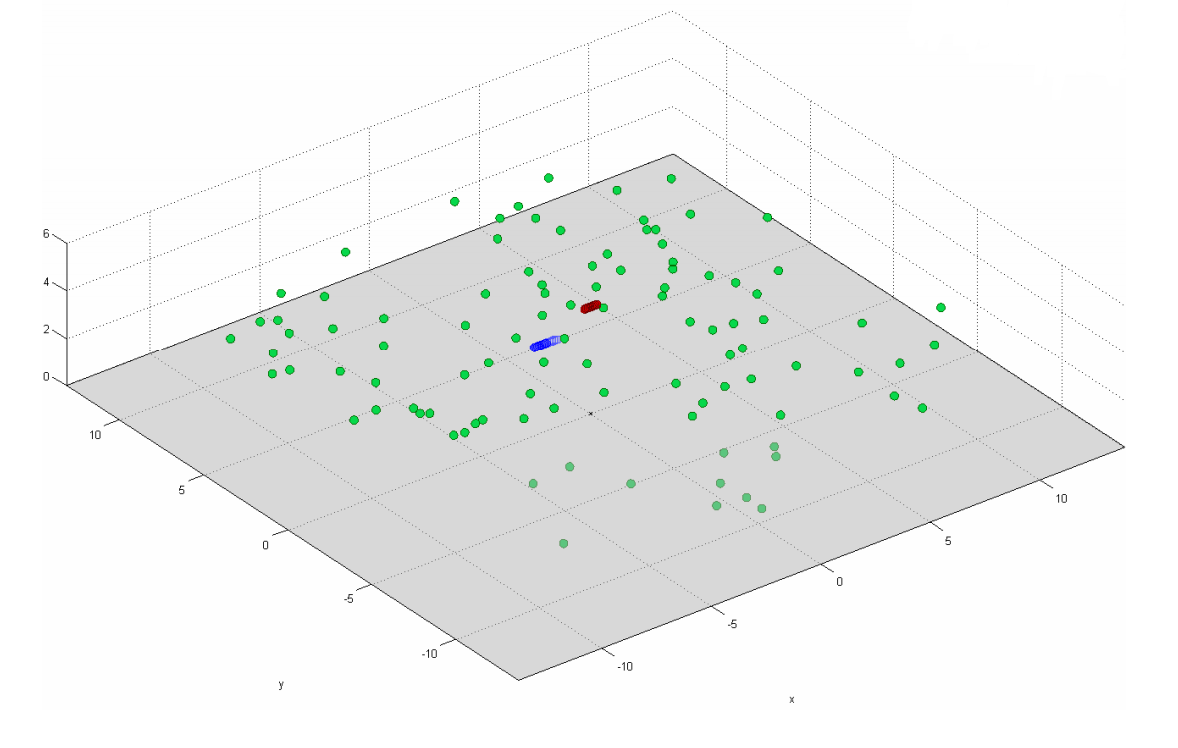
Fig. 17. Modelo de difusores no caso de correlação receptor e transmissor. Pontos verdes significam difusores, receptor e transmissor azuis e vermelhos.

Para consolidar o que aprendemos e ver como a correlação espacial complica a vida, vamos tentar calcular a largura de banda dos canais. Por exemplo, para MIMO 2x2.

Para fazer isso, usamos os seguintes casos (queremos dizer o mesmo desvanecimento plano, por simplicidade, também consideramos apenas o canal Rayleigh):

1) canal espacialmente branco;
2) Modelo Kronecker com uma correlação relativamente fraca:

$\ mathbf {R} _T = \ mathbf {R} _R = \ begin {bmatrix} 1 e 0,4 \\ 0,4 e 1 \ end {bmatrix}$

3) Modelo Kronecker com uma correlação relativamente forte:

$\ mathbf {R} _T = \ mathbf {R} _R = \ begin {bmatrix} 1 e 0,6 \\ 0,6 e 1 \ end {bmatrix}$

Usaremos o Python 3.4 nesta parte. A função para calcular a largura de banda será obtida em uma das minhas publicações anteriores .

 import numpy as np from numpy import linalg as LA import matplotlib.pyplot as plt from scipy.linalg import fractional_matrix_power def openloop_capacity(H_chan, SNR_dB): SNR = 10**(SNR_dB/10) Mt = np.shape(H_chan)[1] H_sq = np.dot(H_chan,np.matrix(H_chan, dtype=complex).H) lambdas = LA.eigvals(H_sq) lambdas = np.sort(lambdas)[::-1] c = 0 for eig in lambdas: c = c + np.log2(1 + SNR*eig/Mt) return np.real(c)

Defina os principais parâmetros do sistema:

 Mr = 2 # number of receive antennas Mt = 2 # number of transmit antennas Rr1 = np.array([[1., .4], [.4, 1.]]) # case 1 Rr2 = np.array([[1., .6], [.6, 1.]]) # case 2 Rt1 = np.array([[1., .4], [.4, 1.]]) # case 1 Rt2 = np.array([[1., .6], [.6, 1.]]) # case 2 Rr1_half = fractional_matrix_power(Rr1, 0.5) Rr2_half = fractional_matrix_power(Rr2, 0.5) Rt1_half = fractional_matrix_power(Rt1, 0.5) Rt1_half_H = np.conj(Rt1_half).T Rt2_half = fractional_matrix_power(Rt2, 0.5) Rt2_half_H = np.conj(Rt2_half).T

Iniciamos a simulação:

 counter = 1000 SNR_dBs = [i for i in range(1, 21)] C_MIMO_uncorr = np.empty((len(SNR_dBs), counter)) C_MIMO_kron1 = np.empty((len(SNR_dBs), counter)) C_MIMO_kron2 = np.empty((len(SNR_dBs), counter)) C_MIMO_kron3 = np.empty((len(SNR_dBs), counter)) C_MIMO_kron4 = np.empty((len(SNR_dBs), counter)) for c in range(counter): H_uncorr = (np.random.randn(Mr,Mt) + 1j*np.random.randn(Mr, Mt))/np.sqrt(2) H_kron1 = np.dot(Rr1_half, np.dot(H_uncorr, Rt1_half_H)) H_kron2 = np.dot(Rr2_half, np.dot(H_uncorr, Rt2_half_H)) for idx, SNR_dB in enumerate(SNR_dBs): C_MIMO_uncorr[idx, c] = openloop_capacity(H_uncorr, SNR_dB) C_MIMO_kron1[idx, c] = openloop_capacity(H_kron1, SNR_dB) C_MIMO_kron2[idx, c] = openloop_capacity(H_kron2, SNR_dB) C_MIMO_uncorr_erg = np.mean(C_MIMO_uncorr, axis=1) C_MIMO_kron1_erg = np.mean(C_MIMO_kron1, axis=1) C_MIMO_kron2_erg = np.mean(C_MIMO_kron2, axis=1)

Desenhando

 plt.figure(figsize=(7, 5), dpi=100) plt.plot(SNR_dBs, C_MIMO_uncorr_erg,'g-o', label='Uncorrelated') plt.plot(SNR_dBs, C_MIMO_kron1_erg, 'm-o', label='Kronecker model, case 1') plt.plot(SNR_dBs, C_MIMO_kron2_erg, 'r-o', label='Kronecker model, case 2') plt.title("Rayleigh flat fading (MIMO 2x2)") plt.xlabel('SNR (dB)') plt.ylabel('Ergodic capacity (bps/Hz)') plt.legend() plt.minorticks_on() plt.grid(which='major') plt.grid(which='minor', linestyle=':') plt.show()

Temos:

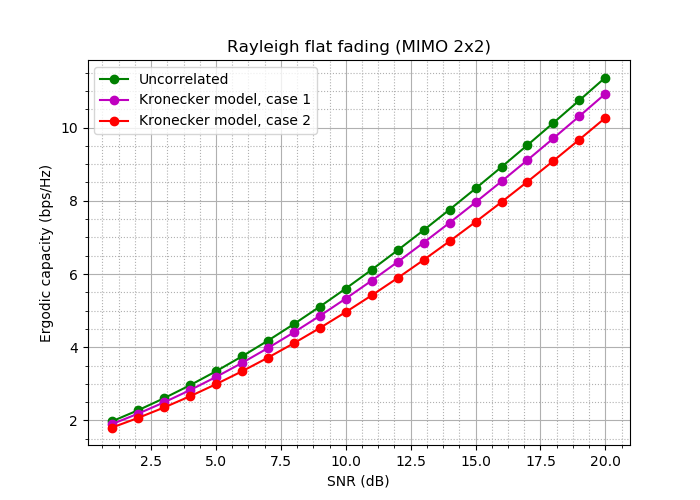
Fig. 18. Curvas de largura de banda para essas experiências.

Bem: a diferença, embora não seja crítica, é!

Posfácio

Talvez um dos leitores tenha notado que quase tudo o que examinamos hoje (em detalhes e de passagem) é muito bom nos parâmetros do objeto matlab comm.MIMOChannel . Este fato me parece muito importante:

em primeiro lugar, sistematiza ainda mais o descrito acima,
e, em segundo lugar, enfatiza que estamos tratando de questões atuais.

Bem, e agora, se você usar esses blocos, espero, ficará mais claro por que e quais canetas você precisa torcer.

Obrigado a todos pela atenção!

Acrescentarei aqui um link para os slides sobre Reiner S. Thomä (Ilmenau), sobre os quais ele nos deu palestras na época. Eu acho que alguém será útil!

Literatura

Paulraj, Arogyaswami, Rohit Nabar e Dhananjay Gore. Introdução às comunicações sem fio no espaço-tempo. Cambridge University Press, 2003.
Goldsmith A. Comunicações sem fio. - Cambridge University Press, 2005.
Fontæn, Fernando Pærez e Perfecto Mariæo Espiæeira. Modelando o canal de propagação sem fio: uma abordagem de simulação com o Matlab. Vol. 5. John Wiley & Sons, 2008.
Farrokhi, Farrokh R., et al. "Eficiência espectral de sistemas sem fio FDMA / TDMA com conjuntos de antenas de transmissão e recepção". Transações IEEE em comunicações sem fio 1.4 (2002): 591-599.

Quase o canal MIMO mais fácil com desbotamento (modelo Kronecker incluído)