Fractais em números irracionais. Parte 2

Parte 0: Fractais em números primos.
Parte 1: Fractais em números irracionais.



O artigo contém GIF e imagens contrastantes. Epilépticos podem ter uma convulsão epiléptica.

Em um artigo anterior, analisamos um algoritmo de visualização de sequência binária. Vamos lembrar.

Veja a sequência binária. Como exemplo, os primeiros bits de uma sequência fractal discutidos em um artigo anterior:

$$

$$Q_n = \ lfloor n \ sqrt {2} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

0100110110010011001001101100

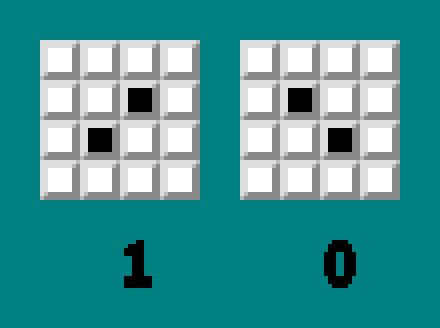
Desenhamos um campo de célula quadrada. Definimos os bits no limite superior. A distância entre os bits é de duas células:



Para cada bit, desenhe um caminho tracejado ao longo da diagonal (através da célula). Para zeros, desenhe o primeiro toque à direita:



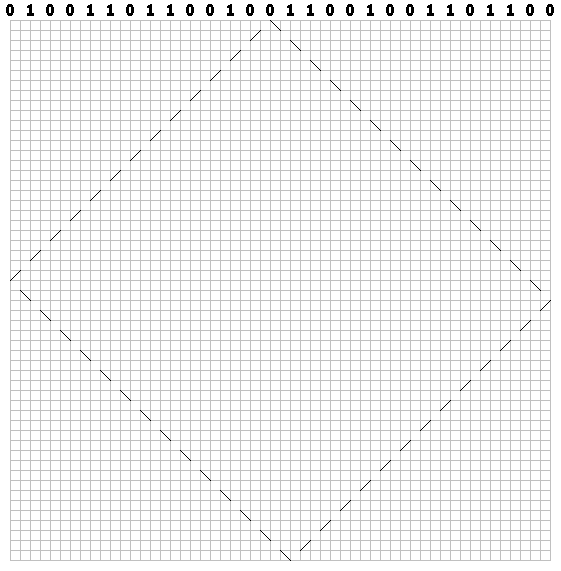
Para unidades - à esquerda:



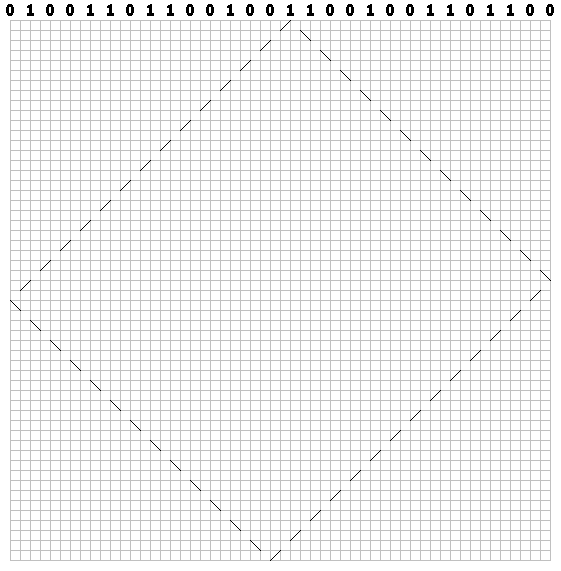
Desenhe uma trajetória para cada bit. Temos um padrão de "bilhar":



Um padrão idêntico (sem um defeito na diagonal - a sequência é infinita, visualizada como uma sequência final) pode ser obtido de outra maneira. Inverta todos os bits pares na sequência:

0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 1 1 1 0 0 1 1 1 0 0 1

Em seguida, para cada bit, desenhe linhas tracejadas verticais:



Colocamos os bits à esquerda, desenhamos linhas horizontais:



Combinamos:



Depois de escrever o primeiro artigo, duas perguntas permaneceram sem solução:

1. É possível desenhar um padrão fractal para números irracionais. Você pode. O problema foi resolvido em um artigo anterior. Na figura acima - parte do padrão fractal para $$$\ sqrt {2}$. Se você selecionar uma das curvas neste padrão:



Obtenha a conhecida curva fractal - "Fibonacci word fractal".

2. A segunda pergunta é se é possível escrever um algoritmo que pinte um padrão:



A segunda questão será abordada neste artigo. Vamos colorir os padrões com a ajuda de um tear, cujo trabalho simulamos usando JavaScript.



No diagrama acima - a máquina mais fácil. Consiste em dois quadros através dos quais os fios são esticados. Os quadros estão conectados aos pedais. Quando você pressiona um dos pedais, um dos quadros sobe. As roscas desenhadas através desse quadro se elevam e uma rosca transversal é esticada no espaço resultante entre as roscas. Se você esticar os fios pares e ímpares através de quadros diferentes, obtém uma trama em um padrão quadriculado:



Em máquinas mais complexas, quatro ou mais quadros são usados:


Tear de mesa de 4 eixos Ashford

Para não se confundirem qual pedal pressionar, eles fazem um diagrama.



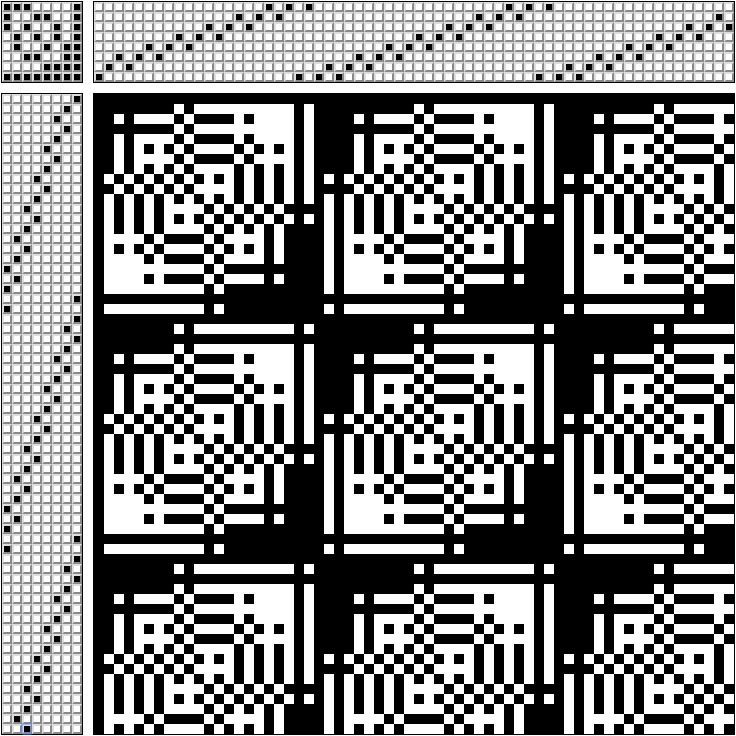
Na parte superior direita do padrão, é indicado através de quais quadros os fios passam (padrão para um tear de 8 quadros).

No canto superior esquerdo - quais pedais prendem ao mesmo tempo (cada pedal é conectado apenas com seu próprio quadro).

Na parte inferior esquerda - em que ordem pedalar.

Na parte inferior direita - que tecido temos. Se você esticar o fio branco através do preto, obtemos um padrão monocromático.

Imediatamente "entrar" no princípio pode parecer um pouco difícil. A figura abaixo mostra como o padrão de tecelagem é formado:



Vamos escrever um script. Nós esticaremos as linhas através dos quadros usando a matriz de matriz unidimensional2. No array unidimensional array1, escrevemos a sequência de aperto dos pedais. No array3 (array binário 8x8), escrevemos quais pedais são fixados ao mesmo tempo.

for(var i=0;i<length;i++){ for(var j=0;j<length;j++){ if(array3[array1[i]][array2[j]]){ context.fillRect(i, j, 1, 1); } } } 

Script (funciona no Google Chrome).

Com a ajuda do nosso tear improvisado, podemos desenhar uma ampla variedade de padrões:



Mas tão historicamente, a pessoa média não tem mais do que duas pernas. Portanto, é conveniente prender simultaneamente não mais do que dois pedais. Um dos padrões mais populares para um tear é o seguinte:



Para 4 quadros. E sua modificação para 8 quadros:



Inesperadamente, os padrões (ou um fragmento de padrões) criados com esse modelo são semelhantes aos nossos padrões de "bilhar". Além disso, esses padrões são sombreados:



Você pode aprender a selecionar padrões de "bilhar" para um tear. Um exemplo:



No início do artigo, já vimos um fragmento desse padrão.

Termine com teares e escreva um script para visualizar seqüências binárias. Podemos nos livrar de uma das matrizes - o padrão é diagonal simétrico. Como preencher a matriz restante? Elementar:



Tomamos a sequência para $$$\ sqrt {2}$. Crie uma matriz. No elemento zero da matriz, escreva o bit zero da sequência. Como alternativa, pegue cada bit da sequência. Se o enésimo bit = 1 - escreva no array a [n] = a [n-1] +1. Se bit = 0 - escreva a [n] = a [n-1] -1

$$

$$Q_n = \ piso n \ sqrt {x} \ piso \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ... \\ a_n = \ begin {cases} a_ {n-1} +1, Q_n = 1; \\ a_ {n-1} -1, Q_n = 0 \ end { cases}$$

  var a=[0]; for(var i=1;i<size;i++){ if(Math.floor(i*Math.sqrt(2))%2==1) a[i]=a[i-1]+1; else a[i]=a[i-1]-1; } 

Verificamos:

  for(var i=0;i<size;i++){ context.fillRect(i, a[i]+50, 1, 1); } 

De fato, já recebemos um fractal elementar, mas continuaremos.

A seguir, trataremos da matriz:



Resumir $$$x$e $$$y$. Divida o módulo por 4. Se o resultado resultante = 0 ou 1 - escreva na matriz true. Para 2 e 3, escreva false. Podemos prescindir de uma matriz (não se sabe antecipadamente quais valores máximos e mínimos um [n] leva). Resuma um [x] e um [y]. Para o valor resultante, adicione algum número $$$C$(para se livrar dos casos em que o valor é um número negativo). Divida o módulo por 4. Para os valores 0 e 1, pinte o pixel com coordenadas $$$x$e $$$y$.

O algoritmo final leva apenas algumas linhas:

  var a=[0]; for(var i=1;i<size;i++){ if(Math.floor(i*Math.sqrt(2))%2==1) a[i]=a[i-1]+1; else a[i]=a[i-1]-1; } for(var x=0;x<size;x++){ for(var y=0;y<size;y++){ q=(a[x]+a[y]+512)%4; if(q==0 || q==1) context.fillRect(x, y, 1, 1); } } 

Visualize nossas seqüências fractais.

$$

$$Q_n = \ lfloor n \ sqrt {2} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Você pode modificar facilmente o script para obter uma imagem RGB:

  q=(a[x]+a[y]+512)%4; /*if(q==0 || q==1) context.fillRect(x, y, 1, 1);*/ if(q==0) context.fillStyle = 'rgb(255,0,0)'; if(q==1) context.fillStyle = 'rgb(0,255,0)'; if(q==2) context.fillStyle = 'rgb(0,0,255)'; if(q==3) context.fillStyle = 'rgb(0,0,0)'; context.fillRect(x, y, 1, 1); 

Acima, adicionamos um número à soma a [x] + a [y] $$$C$. Se você não adicionar esse número, o valor mínimo da soma = -8, o máximo = 8 (para $$$x$e $$$y$de 0 a 750). Se você remover $$$C$- em alguns casos, a soma é negativa e não é um múltiplo do quarto e, nesses casos, o pixel não é pintado por cima (permanece preto):

  q=(a[x]+a[y])%4; if(q==0 || q==1) context.fillRect(x, y, 1, 1); 

Você pode imaginá-lo como se uma parte do fractal estivesse abaixo de alguma borda imaginária (abaixo dessa borda, apenas os valores negativos são múltiplos de 4: -4, -8, -12, ...).

Podemos ver onde está essa fronteira:

  if(a[x]+a[y]>=0) context.fillRect(x, y, 1, 1); 

Em vez de dividir o módulo, podemos comparar a soma com um determinado valor específico e, assim, pintar apenas uma "camada" do fractal. Como exemplo, calcule a média entre os valores mínimo e máximo:

  q=(a[x]+a[y]); if(q==0) context.fillRect(x, y, 1, 1); 

Alterando os valores de mínimo para máximo, podemos ver como as "camadas" na dinâmica mudam:




Além disso, podemos "na testa" comparar um [x] com um [y] e também obter um padrão fractal:

 if(a[x]==a[y]) context.fillRect(x, y, 1, 1); 

A seguinte sequência:

$$

$$Q_n = \ lfloor n (\ sqrt {2} +1) \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Fractal:



RGB:



Camada intermediária:



Em dinâmica:

$$

$$Q_n = \ lfloor n \ sqrt {3} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Fractal:



RGB:



Camada intermediária:



Em dinâmica:

$$

$$Q_n = \ lfloor n (\ sqrt {3} +1) \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Fractal:



RGB:



Camada intermediária:



Em dinâmica:

$$

$$Q_n = \ lfloor n \ sqrt {5} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

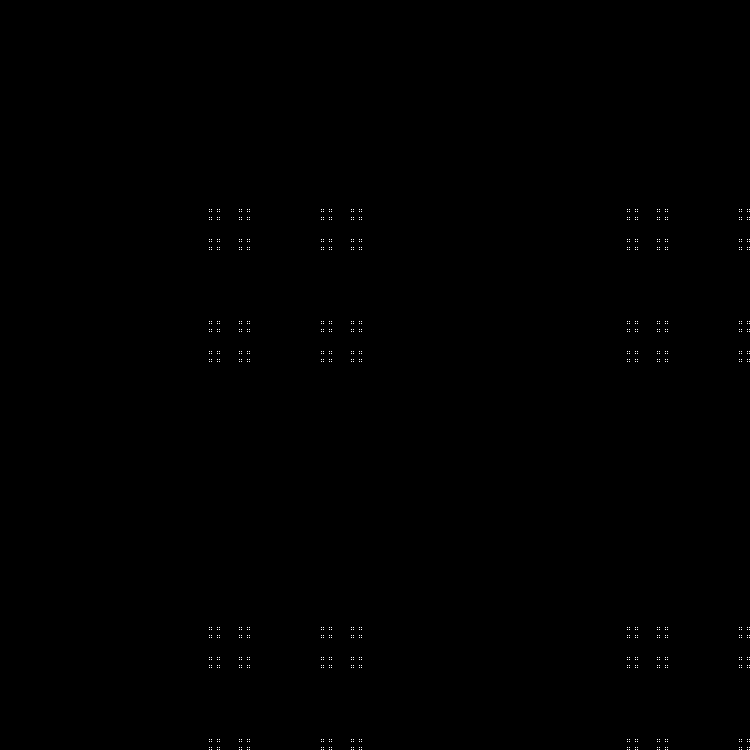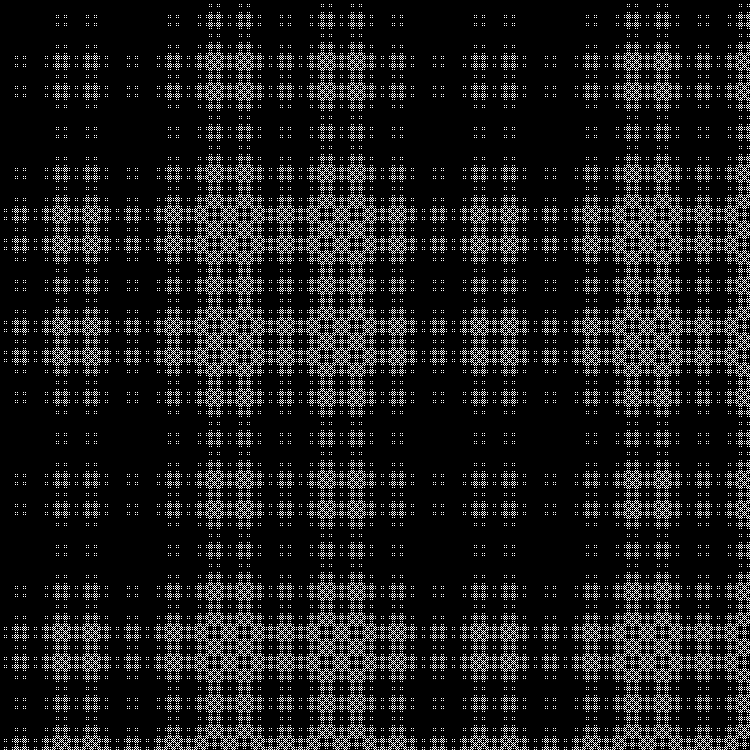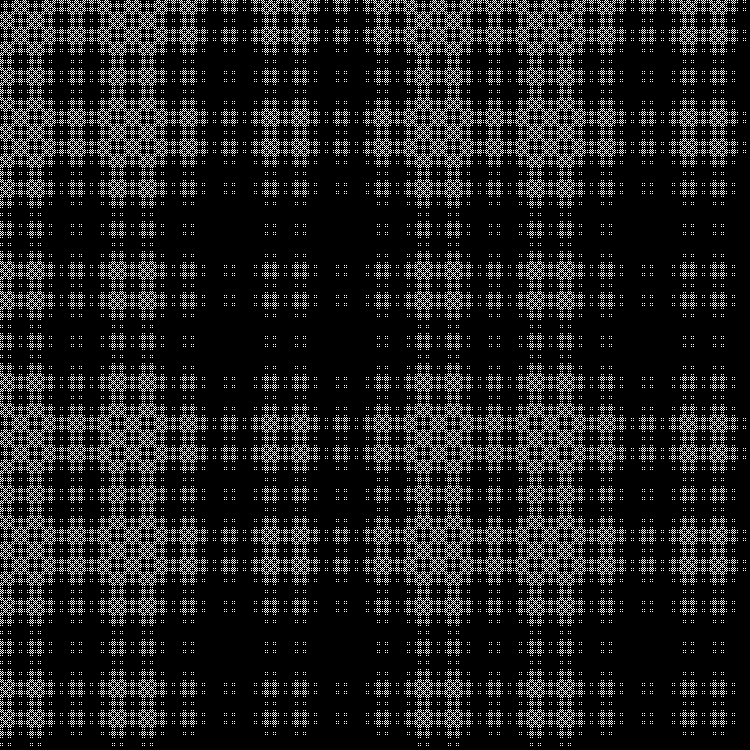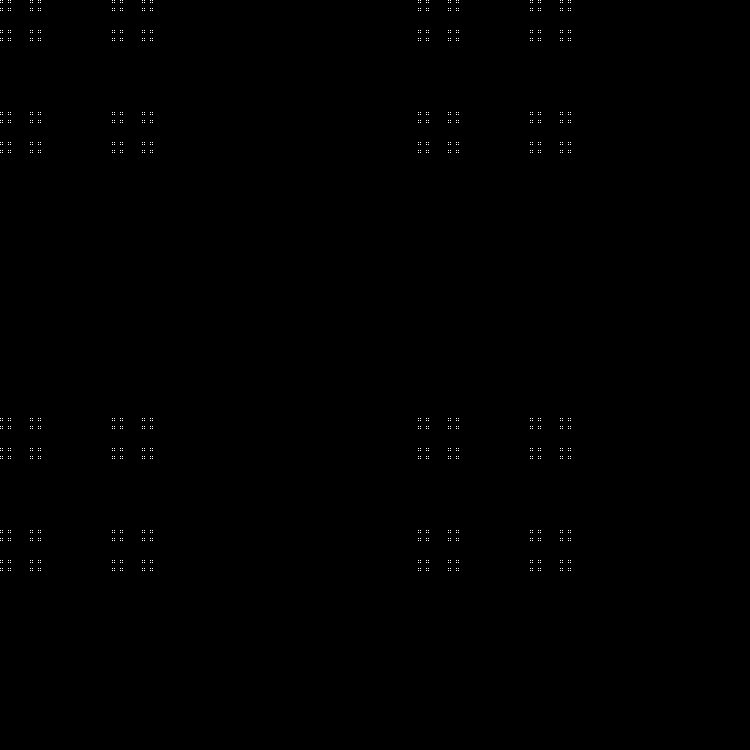
Fractal:



RGB:



Camada intermediária:



Em dinâmica:



Bem, nosso fractal favorito (parte desse padrão pode ser desenhado usando bilhar, com tamanhos laterais iguais aos números de Fibonacci):

$$

$$Q_n = \ lfloor n (\ sqrt {5} +1) \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Fractal:



RGB:



Camada intermediária:



Em dinâmica:



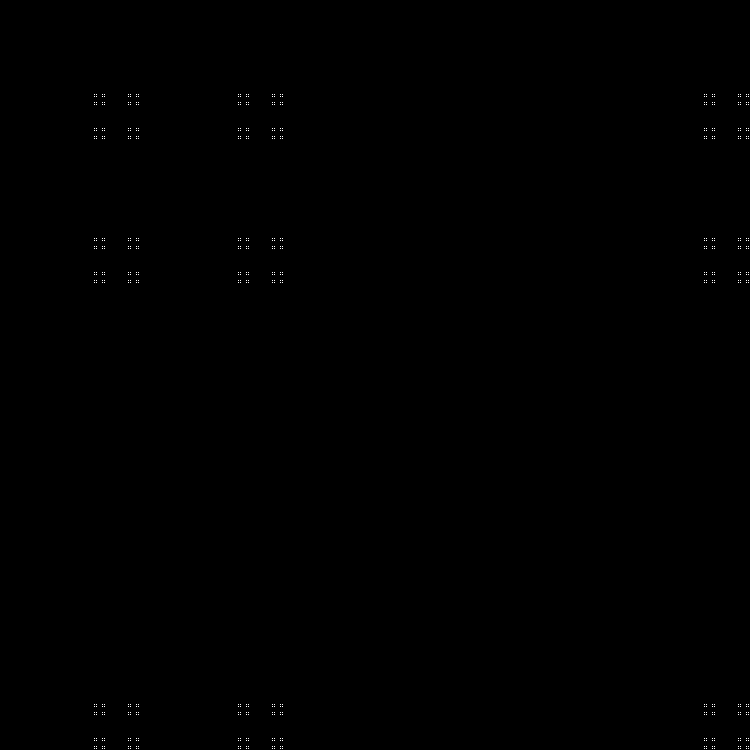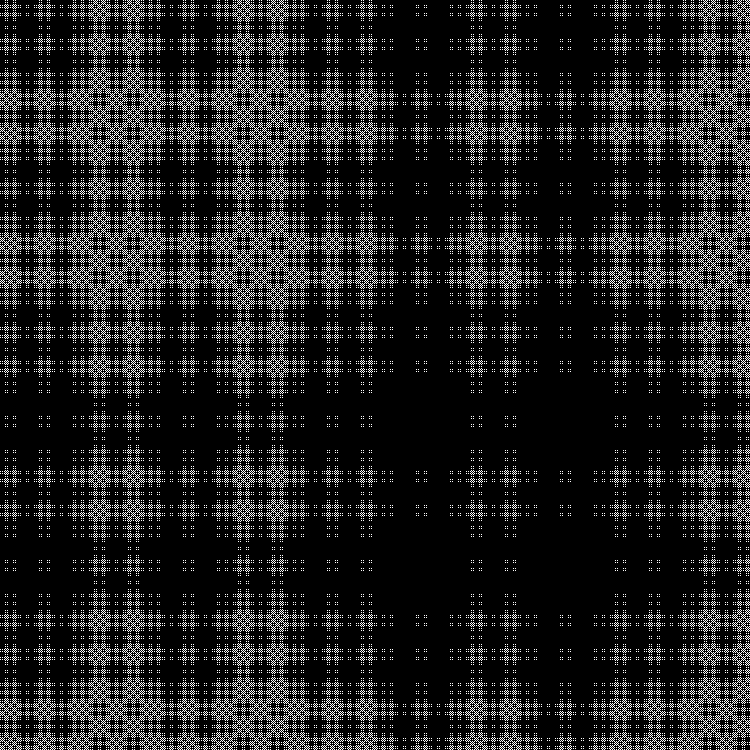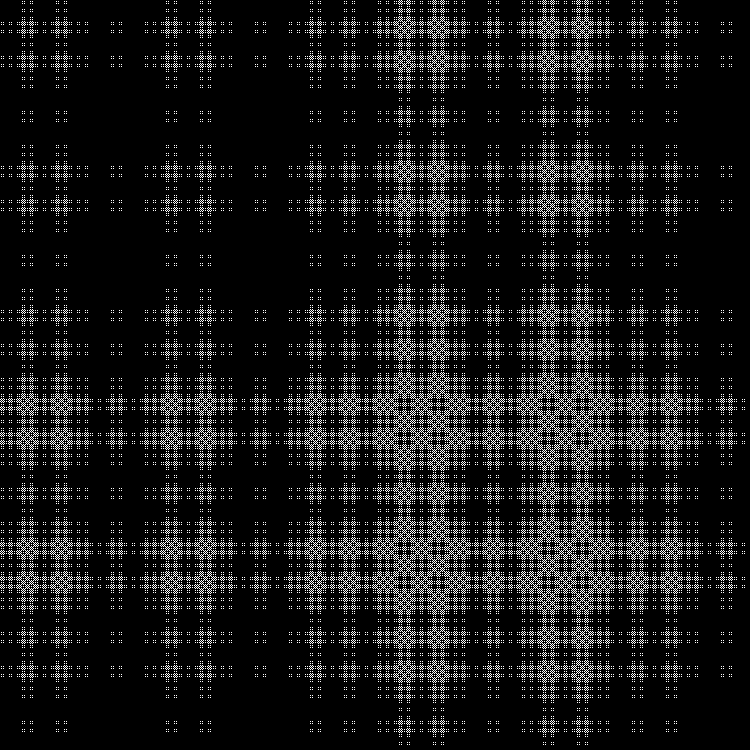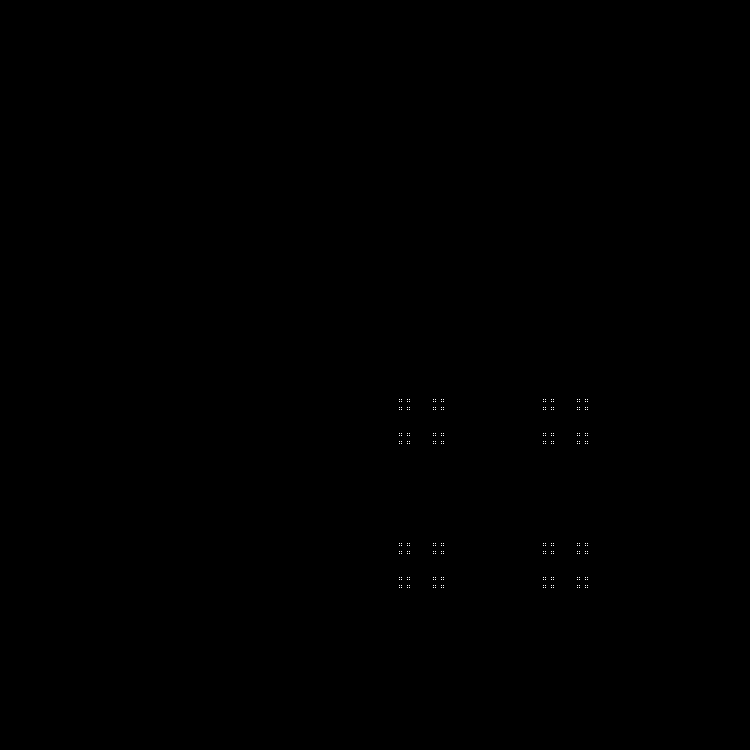
Outra sequência para concluir:

$$

$$Q_n = \ lfloor n ^ {2} \ sqrt {2} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Padrão:



RGB:



Camada intermediária:



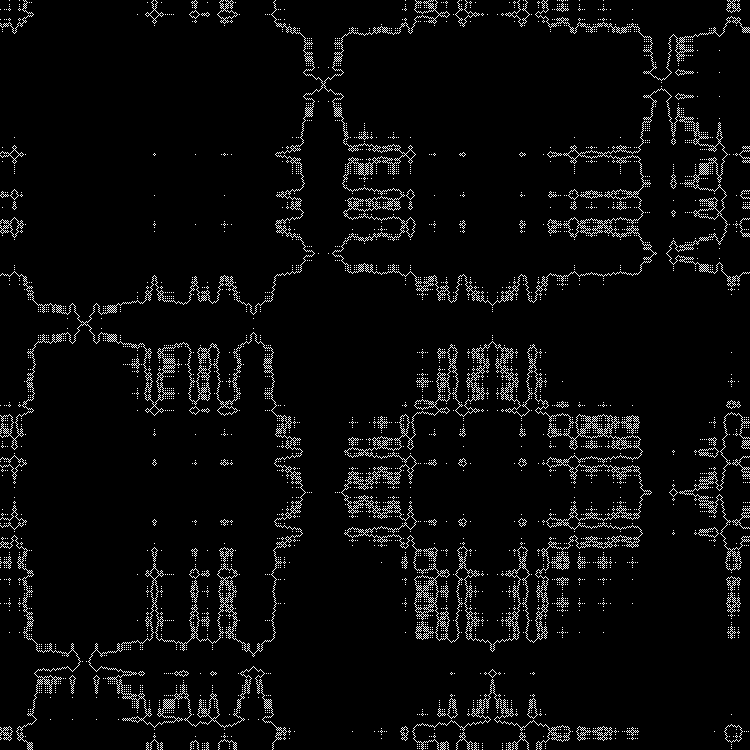
Em dinâmica:



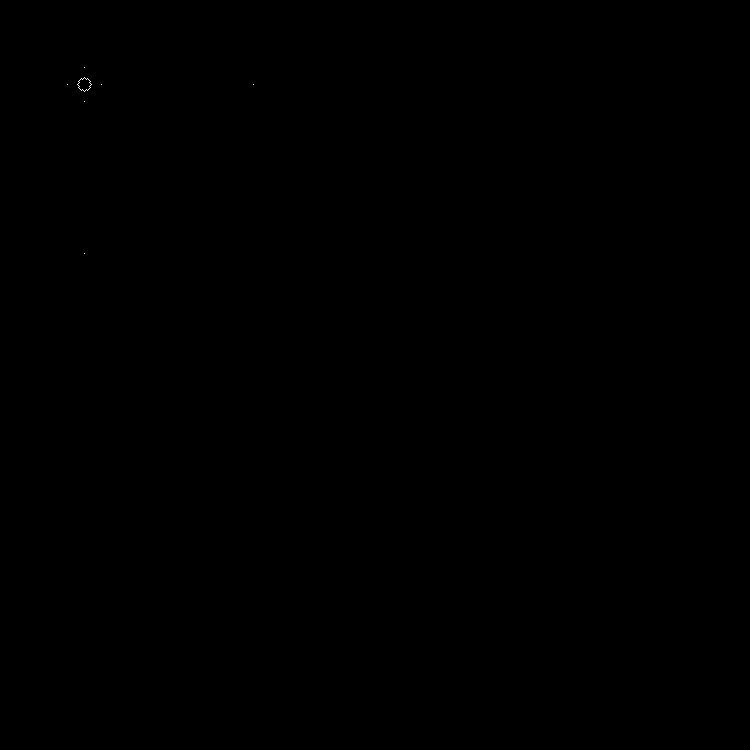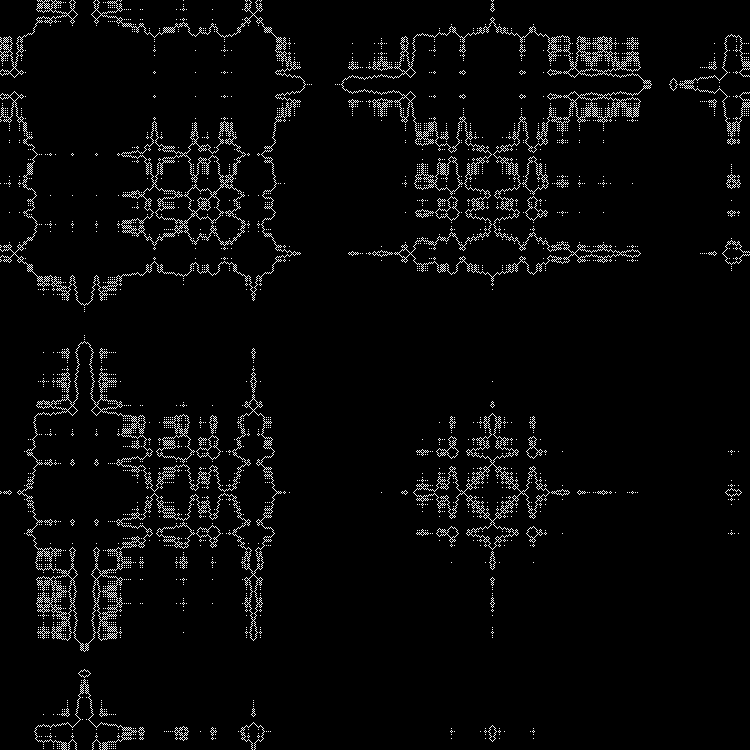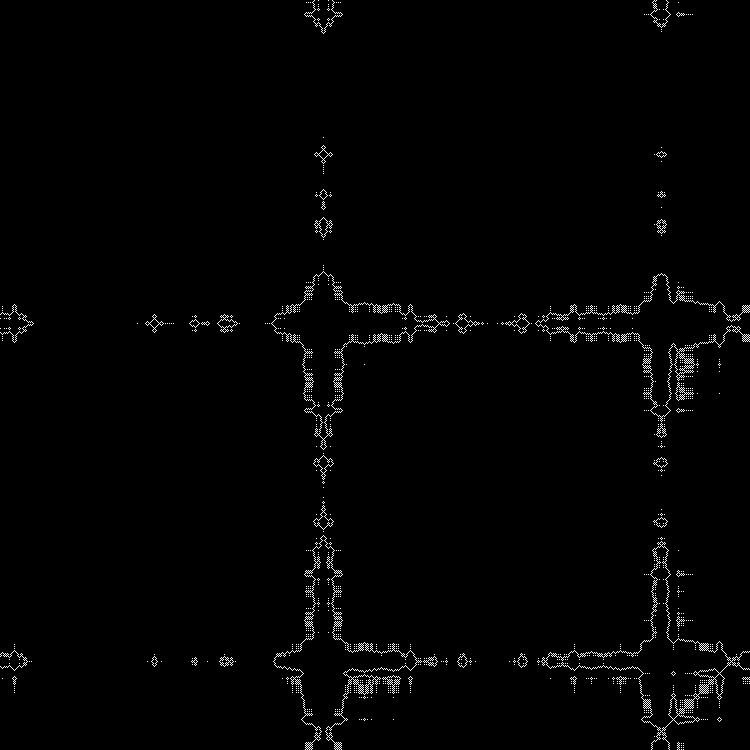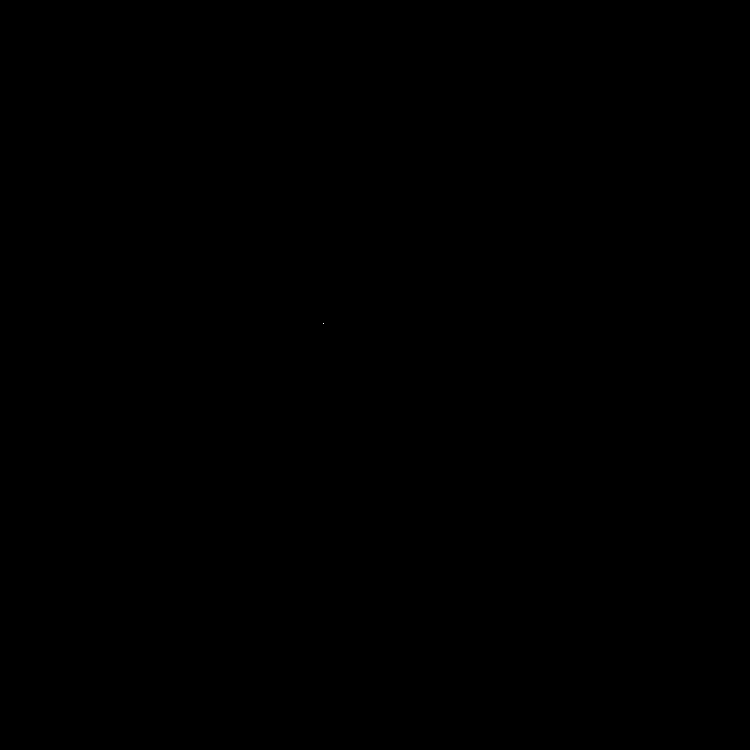
Outras raízes quadradas podem ser inseridas no script . (Você pode dirigir em valores fracionários).

No segundo script, você pode conduzir a sequência manualmente.

Outro script para bilhar. Coordenadas do mouse - dimensões do bilhar. O padrão à esquerda é formado a partir da sequência obtida usando o restante da divisão (detalhes no artigo anterior). No lado direito - paridade $$$\ piso n \ frac {y} {x} \ piso$.