1. Introdução

Sobre o projeto

O projeto “Taxa de câmbio absoluta” está envolvido na análise de taxas de câmbio emparelhadas, na alocação de taxas de câmbio absolutas delas e em suas análises. No âmbito do projeto, foi obtida uma metodologia para a conversão de taxas de pares em taxas de câmbio absolutas. Para isso, a moeda absoluta ABS é definida. Todas as moedas disponíveis são expressas em termos de ABS.

Uma descrição detalhada da tecnologia é fornecida no artigo "De pares de moedas a taxas de câmbio absolutas" .

Sobre o problema

Este artigo aborda o problema de uma análise qualitativa da coerência das taxas de câmbio.
A necessidade de estudar o relacionamento entre moedas se deve aos requisitos para a seleção de instrumentos financeiros na carteira de investimentos e à capacidade de prever o comportamento das moedas com base em dados de outras moedas a elas associadas.

É aconselhável incluir instrumentos com alta conectividade multidirecional no portfólio de investimentos. Isso permite reduzir o risco geral do portfólio.

E, se você encontrar ferramentas com um alto grau de conexão, com base no comportamento de alguns, poderá prever o comportamento de outros.

Sobre o experimento

Seleção de método

Como dados iniciais do experimento, existem séries de dados com taxas de câmbio absolutas (consulte o arquivo de origem. Folha “Taxas de câmbio absolutas” ).



Para estudar a conectividade de uma série de dados numéricos, é melhor usar a correlação de Pearson (consulte Correlação - Wikipedia ).

O coeficiente de correlação tem um intervalo de valores de "-1" a "+1". Valores negativos grandes indicam uma forte relação multidirecional. Valores positivos grandes indicam forte conectividade unidirecional. A proximidade do coeficiente para "0" indica a ausência de comunicação.

O que você quer receber?

O objetivo do experimento é obter grupos de moedas com um alto grau de conexão. Além disso, o sinal de comunicação também é interessante.

Local de encontro

Todos os cálculos serão realizados no sistema Wolfram Mathematica (consulte Wolfram Mathematica - Wikipedia ). E usaremos os recursos de nuvem gratuitos do Wolfram.Cloud .

O recurso especificado permite criar blocos de anotações on-line com cálculos e fornecer acesso para visualização geral. O caderno deste experimento está localizado aqui .

Planejar

Faremos os cálculos de acordo com o plano a seguir.

Primeiro, calculamos a matriz de correlação. As colunas e linhas da matriz corresponderão a moedas individuais. Na interseção da coluna e da linha, estará o coeficiente de correlação do par.

Em seguida, selecionamos pares de moedas com os laços mais fortes. Coloque os pares selecionados no gráfico (consulte Gráfico (matemática) - Wikipedia ).

Os nós do gráfico são moedas. As arestas do gráfico indicarão a relação entre as moedas. A cor da nervura indicará o sinal de colagem. Verde indica um relacionamento positivo e vermelho indica um relacionamento negativo.

A sequência de cálculos indicada será realizada tanto para cursos absolutos quanto para suas alterações. Uma análise da relação dos cursos absolutos permite explorar processos lentos (mais de um dia). Uma análise da relação entre mudanças nas taxas de câmbio absolutas nos permitirá investigar as conexões rápidas entre moedas (um dia).

Resultados

Profundidade de amostragem

O arquivo de origem contém dados dos últimos 150 dias. Segundo eles, o cálculo será feito.

Nuvem de moeda

O experimento envolveu 45 moedas.



Uma lista completa de moedas pode ser vista na folha "Resumo da moeda" do arquivo de origem .

Correlação de taxa absoluta

Acima (ver. Plano), foi planejado calcular a matriz de correlação para taxas absolutas. O resultado é mostrado na figura abaixo.



Aqui, o vermelho corresponde a uma conexão positiva e o azul a uma conexão negativa. Para compreensão, é dada uma escala de gradação. Abaixo e à esquerda estão os marcadores de moeda (nomes abreviados).

Gráfico de dependência de taxa absoluta

A matriz de correlação tornou possível distinguir dois grupos de moedas com um alto grau de conexão. Para isso, pares com uma correlação maior que 0,9 foram selecionados e transferidos para o gráfico.



O primeiro grupo reuniu moedas com um alto grau de dependência do dólar americano. Aqui estão as moedas de quatro países árabes que negociam petróleo, o dólar de Hong Kong e o próprio dólar dos EUA. Todas as dependências são positivas (unidirecionais).

O segundo grupo reuniu moedas européias. No centro está o próprio euro e em torno dele as moedas da Polônia, Romênia e Dinamarca. Todas as dependências são positivas (unidirecionais).

Mudanças relativas nas taxas absolutas

Para mais pesquisas, calculamos as séries de mudanças relativas nas taxas absolutas. A fórmula para os cálculos é a seguinte.



A diferença entre valores sucessivos será correlacionada à anterior das duas. Assim, receberemos uma mudança relativa na taxa absoluta.

Correlação de mudanças relativas nas taxas absolutas

Quanto aos cursos absolutos, obtemos uma matriz de correlação para medidas relativas dos cursos absolutos. Damos uma exibição gráfica da matriz.



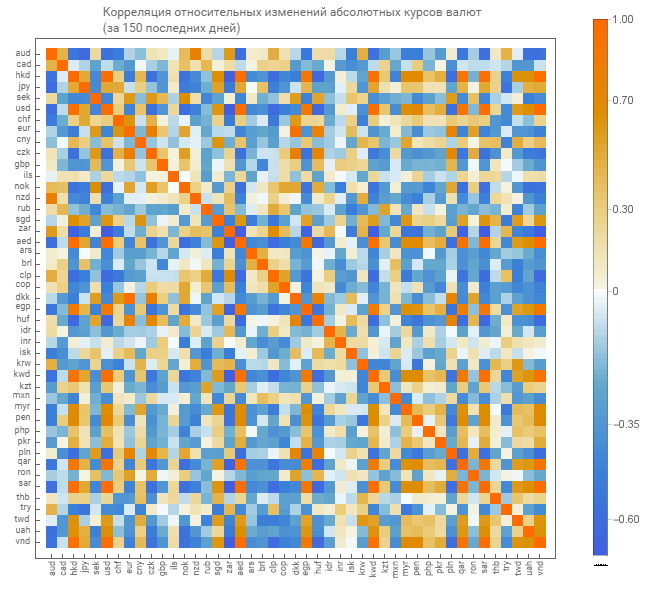
Já existe uma matriz de tons mais claros. O que indica um menor grau de conexão.

Gráfico de dependência de mudanças relativas nas taxas absolutas

A partir da matriz de correlação de mudanças relativas, selecionamos pares de moedas com um alto grau de conexão. Somente o nível de amostragem aqui já é de 0,6 (aqui e acima, esse coeficiente foi escolhido a partir da consideração de um pequeno número de pares para saída no gráfico).



No caso de mudanças relativas recebidas 3 grupos de moedas. O grupo superior combinou as moedas da Austrália e da Nova Zelândia. O grupo inferior reuniu moedas européias. O grupo do meio do dólar de Hong Kong combinou as moedas dos Estados Unidos, Vietnã, cinco países árabes - exportadores de petróleo, África do Sul e Peru.

Além disso, há uma característica interessante na alta dependência negativa do rand sul-africano.

Conclusões

Como resultado do experimento, conseguimos obter o seguinte.

Colocar os dados da matriz de correlação em um gráfico matemático é uma boa prática de visualização para a matriz de correlação. A aplicação adicional deste método simplificará o entendimento dos relacionamentos no grupo de séries numéricas.

É encontrado um método formal para agrupar mercados de moeda. Foi possível distinguir formalmente os mercados da Europa, América e Ásia e Oceania. Esse método pode reduzir significativamente o caminho para revelar as influências mútuas entre os mercados de diferentes países e se tornar uma boa ferramenta para um analista financeiro.

A inclusão do rand sul-africano na carteira de investimentos, juntamente com o dólar americano, reduzirá os riscos dessa carteira.

Catálogo de artigos